斜向激振模式下振动轮滞回耦合特性分析

斜向激振模式下振动轮滞回耦合特性分析

郑书河1，林述温2

(1.福建农林大学机电工程学院,福州350002；2. 福州大学机械工程及自动化学院,福州350108)

摘要：据斜向激振模式下振动压实土壤的水平、垂直两方向滞回恢复力与位移间所呈不同滞回形态，考虑土壤密实度较高时振动轮在土壤面层水平方向发生的脱耦打滑、垂直方向发生脱耦跳振现象，采用仅据土壤特性参数的水平对称、垂直不对称滞回模型，分阶段按工况建立系统动力学方程；在一次近似前提下，利用谐波线性法将非线性作用力线性化为等效刚度及等效阻尼。通过数值计算，研究斜向激振下振动轮水平、垂直方向非线性滞回响应及相互耦合特性，分析压实进程中振动轮发生连耦、滑转及跳振工况下响应特性及工况相互转换规律。结果表明，压实进程中合理调整激振参量，一定程度可避免振动轮发生跳振、打滑现象，从而保证压实质量、效率及驾驶舒适性。

关键词：智能振动压路机；斜向激振模式；滞回模型；滑转；跳振；耦合特性

中图分类号:U415.512；O322文献标志码：A

基金项目：国家自然科学基金资助项目(51275524)

收稿日期：2015-02-12修改稿收到日期：2015-04-03

Analysis on the coupled hysteresis characteristic of intelligent vibratory roller under slant excitation mode

ZHENGShu-he1,LINShu-wen2(1. College of Mechanical Electrical Engineering & Automation, Fujian Agriculture and Forestry University, Fuzhou 350002, China; 2. College of Mechanical Engineering & Automation, Fuzhou University, Fuzhou 350108, China)

Abstract:The resilience of the drum of a vibration roller in horizontal and vertical directions reveals a hysteresis pattern different from that of the displacement during slant excitation compaction. When the soil compactness is high enough, the jump vibration and slipping of the vibration roller may appear. Considering the two facts mentioned above, kinetic equations under various compaction conditions and at different stages were established in terms of a model with horizontal symmetric hysteretic and vertical asymmetric hysteretic curves according to soil property parameters. According to the first order approximation, the hysteretic resilience was linearlized and its equivalent damping coefficient and equivalent stiffness coefficient were deduced by using the harmonic linearization method. By means of numerical simulation, the hysteresis characteristics under three compaction conditions and correlated coupled properties between horizontal and vertical directions, namely, the contraction vibration, slip-rolling and jump vibration were in turn analyzed, and the traufer between them was revealed. The adjustment of excitation amplitude and excitation frequency could availably restrain the jump vibration and slipping of the drum to ensure the compaction quality, efficiency and driving comfort in the compaction process.

Key words:intelligent vibratory roller; slant excitation mode; hysteresis model; slip-rolling; jump vibration; coupled characteristics

振动压路机动力学研究均针对垂直振动或水平振荡提出的单一模式振动模型[1-3]，而对智能振动压路机在斜向激振模式下既有水平振动又有垂直振动模型研究鲜有报道[4]。考虑物料在压实进程中产生塑性变形，水平、垂直方向的弹塑性变形路径不同，导致物料对振动轮的恢复力与位移间形成滞回环形态差异，且施工中压路机振动轮与压实物料间可能产生连耦、打滑、跳振及相互转换的复杂性，而单一模式滞回模型难以全面描述与表征[5-7]。本文考虑斜向激振模式下振动压实土壤的水平、垂直方向弹塑性变形及差异，用仅依据土壤特性参数的水平对称、垂直不对称滞回模型表征土壤压实进程中滞回力与变形的滞回特性，研究振动轮在水平、垂直方向相互耦合的响应特性，揭示振动轮发生连耦、跳振、打滑等复杂工况下力学特性及各工况相互转化规律，旨在为压路机设计、施工作业中合理配置工作参数提供理论依据。

1滞回动力学模型

振动轮在未发生打滑、跳振情况下始终与物料保持接触，物料受周期作用力，忽略参数慢变、物料滞回恢复力，见图1。设初始刚度为k1，振动轮正向运动，达到屈服极限开始塑性变形阶段为A-B，因塑性变形量较小可忽略；继续加载至正向运动极限点B后振动轮开始反向运动，反向达到屈服极限点C后继续加载阶段C-D；到达反向运动极限点D后再进入新的加载阶段D-E。而在垂直反向中，滞回力回到平衡点C′(滞回力为0)形成卸载阶段B-C′,由于振动轮不能对物料向上施加拉力，物料不会产生与向下相同的弹塑性变形，出现不对称滞回曲线C′-D′，达到反向运动极限点后又进入加载阶段D′-E。由于计算每个周期内恢复力均以上个周期反向卸载终止点为下个周期起点，且正反向加、卸载时物料会产生弹塑性变形，故恢复力与位移形成封闭滞回环，而在水平方向形成对称滞回环A-B-C-D-E，在垂直方向形成不对称滞回环A-B-C′ -D′-E。

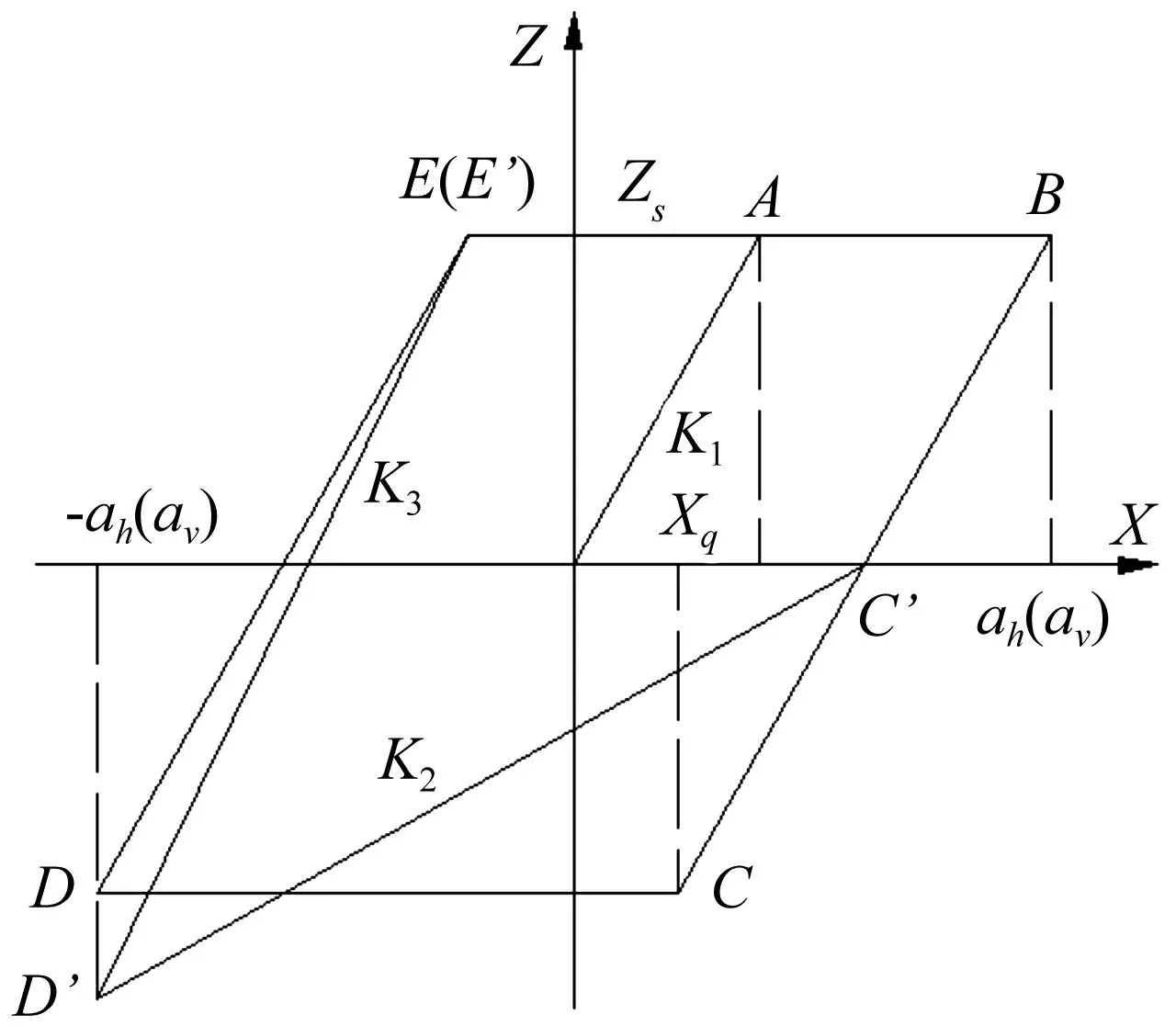
图1　滞回力模型 Fig.1 Hysteretic force model

据图1，滞回力表示为

式中：Z为斜向激振模式下滞回力矩阵；zh，zv为水平、垂直滞回力，表达式为

(1)

(2)

式中：ah，av为振动轮水平、垂直振幅；xh，xv为振动轮水平、垂直位移(设土壤水平、垂直方向特性相同)；k1，xs为物料屈服刚度系数及屈服极限；zs为物料屈服时滞回力；k2为垂直方向反向加载刚度；k3为垂直方向正向重新加载刚度。

2压路机动力学模型

据智能振动压路机结构及工作特性，建立动力学模型见图2。模型参数为：①设压实过程中地面始终仅较少部分参与振动，其质量ms忽略不计；设被压实地面为具有一定刚度、阻尼弹性体，且水平、垂直方向力学特性相同；振动轮与地面相互作用简化为刚度ks、阻尼系数cs及水平、垂直滞回力zh、zv的减振器模型。②机架、振动轮简化为质量mf、md质量块。由于振动压路机前后振动轮激振模式按对称布置，前后振动轮对机架的水平方向运动耦合相互抵消，故忽略机架的水平振动。设振动轮挂在机架的减震器水平、垂直方向减震性能相同，刚度、阻尼系数为kd，cd。③压路机处于任一斜向激振(α∈[0,π/2])模式时，振动轮除垂直方向xv与机架xf二自由度运动外，亦存在水平方向xh及旋转方向xθ的二自由度运动，反映压路机对土壤水平揉搓振荡的压实作用。当α= 0或π/2时，模型退化为单一水平、垂直振动模型。

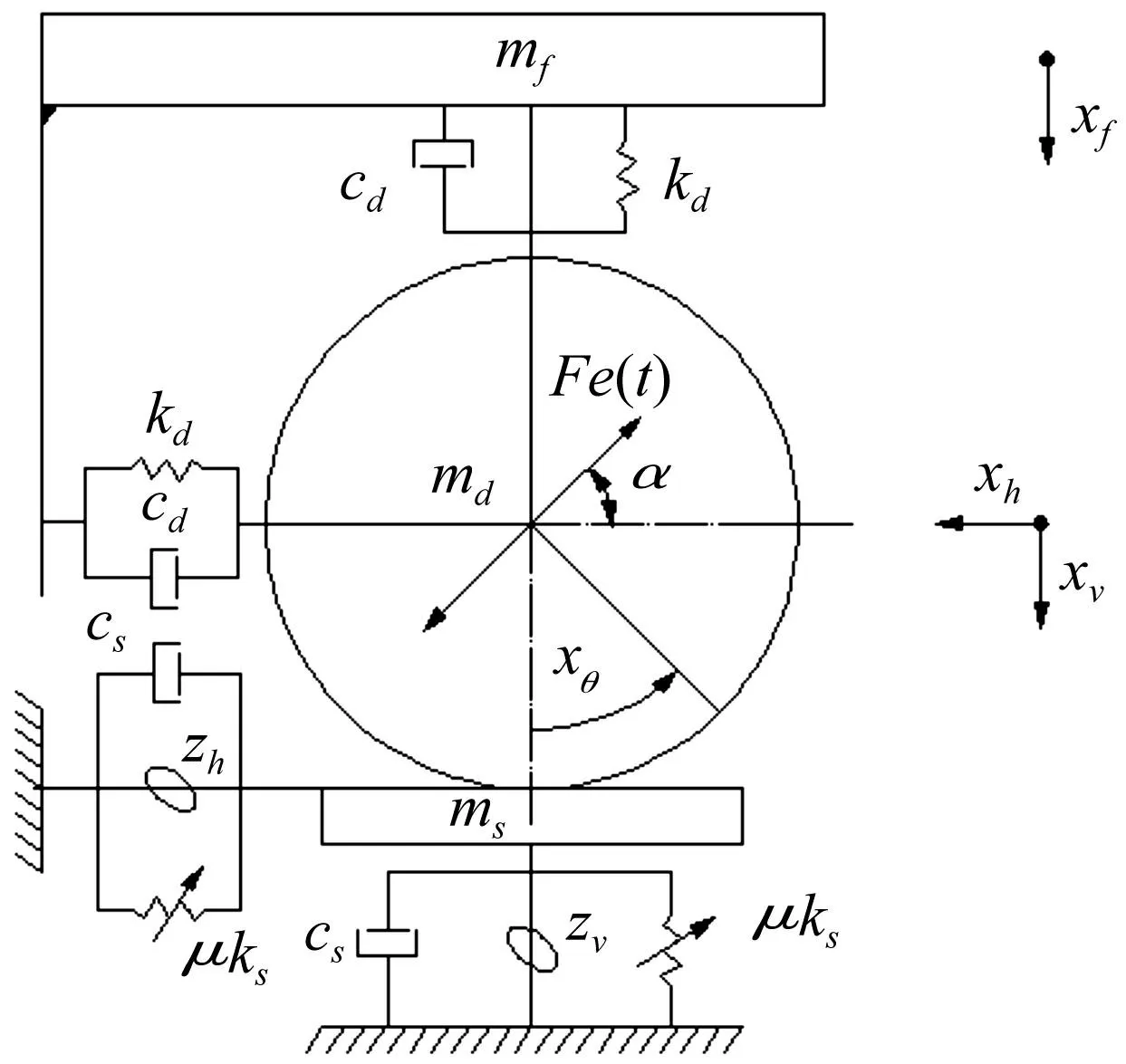
图2　动力学模型 Fig.2 Dynamic model

2.1连耦工况

分析图2知，振动轮与物料间可能存在连耦或脱耦情况。二者保持连耦接触状态系统动力学方程为

(1)水平方向

(3)

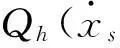
(4)

式中：μ为屈服前后物料刚度之比。

(2)垂直方向

设一次近似解为X=Acosφ+εU1+...，(图1)水平对称滞回曲线A-B-C-D-E中近似假设B-C,C-D,D-E,E-B四线段对应相角范围为0～φc，φc～π，π～φE，φE～2π。其中：ΦC= arccos(xC/ah)；ΦE= π+ arccos(xC/ah)；xC=ah-2xq；xE= -ah+2xq。垂直不对称滞回曲线A-B-C′-D′-E中近似设E-B,B-C′,C′-D′,D′-E对应相角范围为0～φC′，φC′～π，π～φE，φE～ 2π。其中φC=arccos(φC/av)；ΦE= 2π-arccos(xE/av),φC=av-xq，xE= -av+2xq。按谐波线性法，其等效阻尼、等效刚度为

式中：A为振动轮振幅，含水平分量ah及垂直分量av；X为振动轮位移，含水平分量Xh及垂直分量Xv。

积分式(6)可得附录，代入式(3)、(5)按线性理论可得稳态解。

2.2滑转工况

振动轮与压实物料脱离连耦时可能在物料面层打滑或跳离，为此先对打滑脱耦情况进行研究，简化力学模型见图3。由图3可知，振动轮与土壤接触不打滑时其对土壤水平压实力Fs-h为

(7)

且满足

Fs-h=-fs

(8)

式中：fs为土壤面层对振动轮静摩擦力，取值范围0～fmax，fmax为最大静摩擦力，满足

fmax=Fs-vμs

(9)

式中：Fs-v为振动轮对土壤垂直方向压实力；μs为静摩擦系数。

图3　滑转工况动力学模型 Fig.3 Dynamic model of slip-rolling

打滑阶段可将振动轮水平运动分解成两个运动xh=xh1+xp，见图4(a)、(b)。而图3(b)可视为典型带阻尼单自由振动系统，但由于机架与振动轮的减振元件阻尼衰减作用强烈，因此忽略脱耦瞬间扰动，振动轮水平运动xp在脱耦后保持静摩擦力引起的位移较小可忽略，而振动轮在静摩擦力矩作用下(图4(c))，其旋转运动为脱耦阶段的加速运动，水平方向运动微分方程为

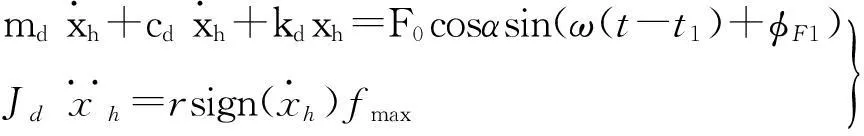
图4　打滑阶段动力学模型 Fig.4 Dynamic model of slip stage

因此，滑转工况下，振动轮从负向最大位移处开始与土壤耦合，运动至土壤摩擦力fs到达最大静摩擦力fmax时发生脱藕打滑，继续正向打滑至最大位移处时重新与土壤耦合，开始另半个周期的耦合、脱耦打滑过程。滑转工况中压路机在垂直方向的动力学方程始终满足式(5)。

2.3跳振工况

振动轮与土壤面层发生脱耦打滑时，由于滑转工况内振动轮水平运动中心与连耦工况运动中心不一致，使系统的运动周期峰值中心产生一定量的偏移畸变。而在垂向，随土壤刚度逐渐增大，振动轮在一定条件下可能跳离土壤面层，此时轮与随振土会完全脱耦为两个独立系统，见图5，系统的运动特性变得更复杂。

图5　跳振工况动力学模型 Fig.5 Dynamic model of jump vibration

由图5(a)，振动轮与土壤面层接触振压，土壤对振动轮垂向压实反力Fs-v可表示为

在一个完整激振周期内，开始时水平压实力较小、Fs-v<(md+mf)g时，振动轮处于接地振压阶段，系统动力学方程符合式(3)、(5)；Fs-v≥(md+mf)g时，振动轮与随振土脱耦，进入跳振阶段。该阶段可将振动轮垂向运动图5(a)分解为图5(b)、(c)，即xv=xv1+xv2，xf=xf1+xf2。图5(c)可视为典型带阻尼单自由振动系统，但由于机架与振动轮的减振元件阻尼衰减作用强烈，因此忽略脱耦瞬间扰动，认为振动轮垂直运动xf2在脱耦后保持重力作用引起可忽略的较小位移。跳振阶段垂向动力学方程为

(12)

式中：t1为发生跳振时刻；ΦF为初始相位。

跳振阶段振动轮水平向为单自由度受迫振动，其动力学方程为

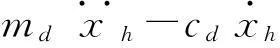
(13)

2.4各工况间转换规律

压实进程中随土壤逐渐密实刚度增大，在斜向激振模式下压实可在三种工况中相互转换，见图6。其中i-j表示工况i向工况j转换，数字1、2、3依次表示连耦、滑转及跳振工况。振动轮与随振土完全脱离连耦发生跳振工况时，振动轮不能从跳振状况直接转换成滑转工况，须待振动轮再次接触土壤面层时方可转换。

图6　工况相互转化关系图 Fig.6 Transition of compaction conditions

3算例仿真

以XG6133D型智能振动压路机为例，已知md=3 000 kg，参考现有压路机实验结果及本机构件特点，选取具体参数[8-9]为

kd=2.0 MN·m-1,cd=0.97 kN·s·m-1

ks=3.2～20 MN·m-1,cs=11～120 kN·s·m-1

k1=1.0,k2=0.6,k3=1.2,Jd=4.7×103

r=1.25 m,u=0.6,μs=0.8,α=0～π/2

压实初期土壤较疏松、且刚度系数小、阻尼系数大，取ks=4.0 MN·m-1，cs=100 kN·s·m-1，xs= 0.001m，F0=168 kN，f=20 Hz，α= π/3。采用龙格-库塔求解方程，忽略暂态过程，积分500周期后的运动，压实系统水平、垂直方向动态响应见图7、图8。

由两图看出，压实初期土壤刚度较小，振动轮受土壤水平压实反力小于最大静摩擦力，垂向压实反力小于压实系统重力，振动轮与随振土处于接触振压连耦工况。在斜向激振模式下，因土壤弹塑性变形的非线性滞回特性，振动轮在水平、垂直方向均发生超谐波共振，但由于两方向振动轮所受土壤恢复力与塑性变形间滞回环形态不同，水平向振动轮频谱呈以基波为主

图7　振动轮水平动态响应图 Fig.7 Horizontal dynamic response of vibratory drum

图8　压路机垂直方向动态响应图 Fig.8 Vertical dynamic response of vibratory roller

仅含高奇次倍谐波特性，且水平位移远大于扭振，而垂向振动轮及机架频谱响应呈以基波为主含各高次倍谐波成分特性。高次倍谐波频谱特征与单自由度对称滞回模型系统用KBM方法所得振动轮解析解吻合[9-10]，表明压实初期振动轮在斜向激振模式下水平及垂直方向发生以基波为主、辅以各高次倍谐波稳定的倍周期运动。

随压实进程土壤逐渐密实、刚度增大、阻尼减小。此时土壤只吸收较小能量，发生较小塑性变形，密实到一定程度后，斜向激振模式中水平分量增大时，振动轮与土壤产生脱耦打滑现象。设压实后期ks=8 MN·m-1cs=50 kN·s·m-1，xs=0.003m，F0= 168 kN，f=20 Hz，α=π/10。对自治系统，相空间流形为

Rn×S。定义全局截面为

采用龙格-库塔求解方程，忽略暂态过程，积分500周期后，仿真见图9。由图9看出，随土壤逐渐密实，振动轮水平、扭转振幅增大，水平运动谱图出现亚谐波共振；压实后期压实力超过最大静摩擦力时，振动轮与土壤面层发生脱耦打滑，振动轮发生亚、超谐波共振，呈现以基波为主含明显的各次亚、超谐波成分频谱，其超谐波频谱中出现较小的明显偶次倍谐波，表明发生打滑现象，偶次倍谐波可认为在打滑阶段，由于扭转运动为依赖初始速度的脱耦加速运动，导致随振土实际水平位移左右不对称而呈非线性滞回特性。水平振动相图表明滑转工况下振动轮处于临界拟周期运动。

图9　滑转工况下振动轮水平方向动态响应图 Fig.9 Horizontal dynamic response of vibratory drum in slip-rolling stage

振动轮在水平向发生打滑工况时，垂向振动轮仍与土壤接地振压。受打滑工况影响，振动轮、机架垂向运动频谱呈较明显的亚谐波及分数倍谐波成分，谱成分更复杂，但呈离散谱，压实系统处于稳定的倍周期运动，见图10。

图10　滑转工况下压路机垂向动态响应图 Fig.10 Vertical dynamic response of vibratory roller in slip-rolling stage

随土壤进一步密实，增大垂直激振分量，振动轮在垂向所受压实反力超过极限值时在土壤面层发生跳振现象，压实系统进入跳振工况。取ks=15 MN·m-1，cs=20 kN·s·m-1，xs= 0.005 m，F0= 168 kN，f=20 Hz，α=9π/10。对自治系统相空间流形为Rn×S，定义全局截面为

采用龙格-库塔法求解微分方程，稳态后仿真见图11。比较图10、图11看出，随进一步密实刚度逐渐增大，阻尼逐渐减小，振动轮位移逐渐负向增大，负不动点集逐渐负向移动，其相图与庞卡莱截面图出现三个奇怪吸引子，且其中出现一个吸引子中负不动点集速度值为负，表明振动轮进入跳振工况，频谱呈丰富的亚谐波及超谐波成分，时域图出现“消顶”，发生亚谐波及超谐波共振，呈复杂的3倍周期运动。随激振幅值增大，在一定条件下振动轮进入复杂的混沌运动。

图11　跳振工况下振动轮垂向动态响应图 Fig.11 Vertical dynamic response of vibratory drum

振动轮在土壤垂直面发生跳振时脱离随振土，在水平方向只发生单自由度受迫振动，动态响应见图12。由图12看出，跳振工况发生时振动轮水平向振动幅值较大，可能影响压路机的驾驶舒适性。而过大振幅会震松振动轮构件的连接部件，影响其机械强度。

图12　跳振工况下振动轮水平振动响应图 Fig.12 Horizontal dynamic response of vibratory drum

由以上分析知，压实进程中随土壤密实度增大，振动轮可在连耦、滑转、跳振三种工况间相互转换。为保证压实质量、提高压实效率，作业中需合理选择激振参量。压实初期土壤较疏松，采用高振幅低频激振模式(F0=168 kN，f=20～30 Hz)，适当情况下可用纯水平或垂直激振模式，振动轮产生稳定的倍周期运动，使级配土壤较快得到密实，保证压实质量前提下提高压实效率。随土壤逐渐密实，至压实中期逐渐增大激振频率(f= 30～40 Hz)，由于阻尼作用，减小振动轮振幅可避免对土壤的冲击破坏，斜向激振模式下适当增大水平分量(α=π/6- π/4)可提高水平振荡揉搓的压实效果。压实中后期，随土壤刚度增大，适当减小激振力幅，防止振动轮在土壤面层发生打滑，影响压实质量。压实末期，土壤刚度增大到一定程度后，为防止振动轮在土壤面层发生跳振，破坏压实质量、保证压路机驾驶舒适性，应进一步提高激振频率、减小激振力幅(高振幅F0= 84 kN，低频f= 40～50 Hz)，一定条件下可采用低振幅高频纯水平激振模式，增强对土壤的水平揉搓振荡压实效果，使土壤充分密实。

4结论

(1)土壤弹塑性变形阶段，由于滞回力的非线性作用，使振动轮波形发生畸变，频谱在水平方向呈以基波为主仅含高奇次倍谐波分量，垂直方向呈以基波为主含各高倍次谐波分量的非线性特性。

(2)随土壤刚度、阻尼变化，压实中后期振动轮在土壤面层产生脱耦打滑，水平方向频谱增加明显的分数倍亚、超谐波，打滑现象发生。谱能量均匀分散，振动轮从倍周期运动进入临界拟周期运动。水平滑转工况下振动轮在垂向响应受打滑影响，频谱呈分数倍亚谐波及超谐波成分，接地振压下发生稳定的倍周期运动。

(3)压实后期，土壤刚度系数增大到一定数值后振动轮与随振土发生脱耦跳振现象，振动轮垂向发生亚谐波及超谐波共振，频谱呈以基波为主含丰富的亚谐波、高次倍谐波成分，在一定条件下系统会进入混沌运动。垂直跳振工况下振动轮在水平方向处于单自由度受迫振动。

(4)压实进程中随土壤参数变化，振动轮可在连耦-打滑-跳振三种工况间相互转化。调整激振参量，一定程度上可避免振动轮在土壤面层产生跳振、打滑现象，以保证压实质量、提高压实效率及驾驶舒适性。

参考文献

[1]Yoo T S, Selig E T. Dynamics of bibratory-roller compaction[J]. Journal of the Geotechnical Engineering Division, 1979, 105(10): 1211-1231.

[2]韩清凯,闻梆椿. 一种非对称滞回受迫振动系统及其分析[J]. 振动工程学报,1998,11(30): 291-296.

HAN Qing-kai, WEN Bang-chun. Analysis of a forced vibration system with asymmetrical hysteresis[J]. Journal of Vibration Engineering, 1998, 11(30): 291-296.

[3]Beainy F, Commuri S, Zaman M. Dynamical response of vibratory rollers during the compaction of asphalt pavements[J]. Journal of Engineering Mechanics,2014,140(7):4014039.

[4]郑书河,林述温. 水平激振模式下压实系统动力学过程及响应特性研究[J]. 振动与冲击, 2014,33(2):147-151.

ZHENG Shu-he, LIN Shu-wen. Dynamic process of horizontal excitation compaction system and its response characteristics[J]. Journal of Vibration and Shock, 2014, 33(2):166-168.

[5]Machet J M, Morel L G. Vibratory compaction of bituminous mixes in france[C]. Pavement Construction and Field Control, 1977: 326-340.

[6]孙祖望,卫雪莉,王鹊. 振荡压实的动力学过程及其响应特性的研究[J]. 中国公路学报,1998,11(2): 117-126.

SUN Zu-wang, WEI Xue-li, WANG Que. The dynamic process of oscillatory compaction and its response characteristics[J]. China Journal of Highway and Transport,1998,11(2): 117-126.

[7]Andergg R, Kanfmann K. Intelligent compaction with vibratory rollers-feedback control systems in automatic compaction and compaction control[J]. Journal of the Transportation Research Record,2004,1868(209):124-134.

[8]秦四成. 振动压路机动力学特性分析[D]. 长春: 吉林工业大学, 1998.

[9]郑书河. 多模式激振下压实系统的动力学特性及路面压实密实度预测模型研究[D]. 福州: 福州大学,2014.

[10]Kimura K O. Multiple time scale analysis of hysteretic systems subjected to harmonic excitation[J]. Journal of Sound and Vibration, 2004, 272(3/4/5): 675-701.

[11]Wang Chi-Hsiang, Chang Shuenn-Yih. Development and validation of a generalized biaxial hysteresis model[J]. Journal of Engineering Mechanics, 2007,133(2): 141-152.

附录

第一作者孙健男，博士生，1987年生

通信作者李洪儒男，教授，博士生导师,1963年生

邮箱:bangong_lhr@163.com