弯管结构对流质饲料输送管道流场稳定性的影响分析

■陈爱平 朱松徳

(1.武昌工学院机械工程学院，湖北武汉 430065；2.华中农业大学工学院，湖北武汉 430070）

流质饲料主要通过管道传送，直角弯管是管道系统中的常用部件。实践证明，管道系统中由于弯管失效引起的事故非常常见（如管道破裂、漏液等），剔除外界因素的影响，这些事故往往是由于管内流体流场的不稳定造成的。一般来说，管道内流体的流场越稳定管道系统就越安全。因而找出管道结构对流体流动特性的影响规律对管道系统的安全性和可靠性有着非常重要的意义。

人们在应用计算流体力学（Computational Fluid Dynamics，后文简称CFD）技术对弯管内部流体的流场进行数值模拟并分析其规律方面做了大量的尝试，也取得了很多的成果，但是弯管结构如何达到最优性能，仍然是一个难题。应用CFD商业软件ANSYS FLUENT 14.0,针对直角圆弯管的流场进行数值模拟，研究弯管结构对运输管道流动特性的影响规律。

1 数值模拟

1.1 几何建模与网格划分

研究运输管道内某一直角圆弯管，其原始几何模型如图1所示，管内直径D为108 mm,曲率半径R取216 mm（弯管的曲率直径比R/D为2），弯头间直管段长度L为108 mm。来流段长度取1 080 mm，去流段长度取1 080 mm。通过前处理软件GAMBIT采用六面体结构化网格进行网格划分，整个模型的网格数量在17万左右。

1.2 参数与边界条件的设置

圆管的水力直径为管道的内径D，为108 mm。设管内流体是水，20℃温度下水的密度ρ取值998 kg/m3，动力黏性系数μ取值0.001 003 kg/(m·s)。

边界条件设置：弯管左端为速度入口，来流速度v取2 m/s；弯管右端为压力出口，取标准大气压P=101 325 Pa；管壁均设为壁面：管道外表面，内壁面采用无滑移条件，u=v=w=0。算得雷洛数Re=ρvD/μ=214 923.23，大于临界值400 0，管内流动为湍流。

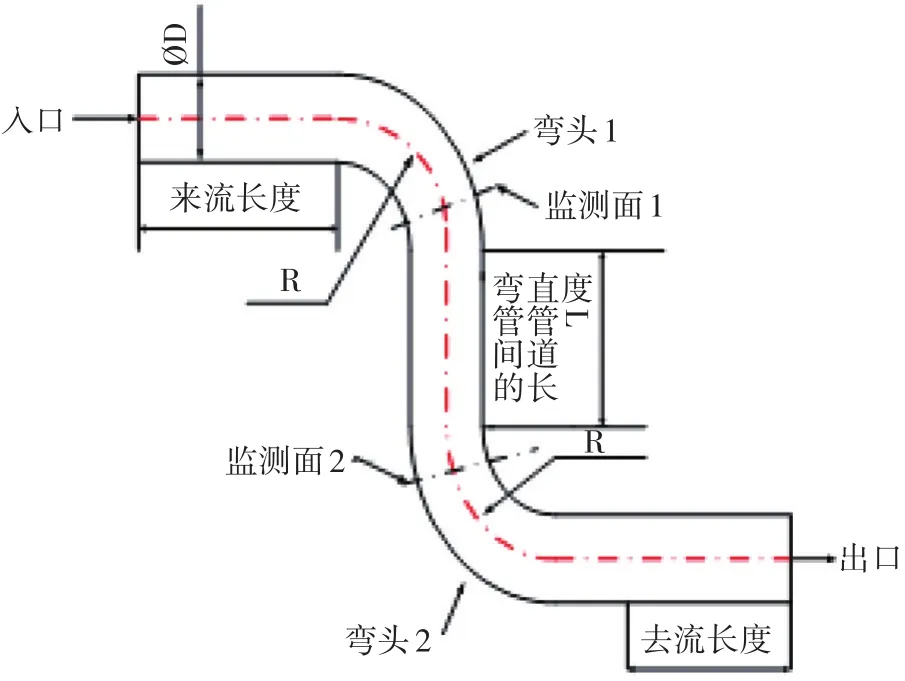
图1 弯管几何模型

1.3 计算模型

1.3.1 控制方程与湍流模型

一般认为，无论湍流运动多么复杂，非稳态的连续方程和Navier-Stokes方程对于湍流的瞬时运动仍然是适用的。假定水为不可压缩黏性流体，通过对瞬态连续方程和Navier-Stokes方程时均化，得到笛卡尔坐标系下不可压流体的控制方程，如式（1）和式（2）所示。数值模拟中，采用RNG K-ε模型，其输运方程见式（3）和式（4）。

其中，各参数取值如下：Cμ=0.084 5，αk=αε=1.39,C1ε=1.42，C2ε=1.68，η0=4.377，β=0.012。

1.3.2 离散格式

将RNG k-ε湍流模型与近壁面无滑移函数处理法相结合，对动量方程、湍动能方程和湍动能耗散率均采用二阶迎风差分格式离散。

模拟计算步骤为：首先给定来流速度，进行定常计算，待其充分收敛之后，再进行非定常计算。

2 模拟结果

应用FLUENT软件对上述原始模型进行数值模拟分析，得到系列结果。图2显示的是弯管内流体的流线图。流体从直管流过弯头之后运动变得紊乱，流线在弯头处发生旋转。图3显示的是管内压力分布情况,可看出弯头处的压力梯度最大。结果揭示：管道系统中弯管结构对管道内流体的流动特性有着极大的影响。下面具体研究弯头结构（直管道长度和弯头曲率）对流动特性的影响规律。

图2 双弯头弯管流线图

图3 双弯头弯管压力分布

3 弯管结构对管道流动特性的分析

3.1 两弯头间的直管道长度L

为了研究L对流体流动特性的影响规律，设定弯管直径D取108 mm,来流段长度1 080 mm，去流段长1 080 mm，对L取四种不同的数值，应用FLUENT软件对流体流动特性分别进行模拟分析。

3.1.1 流线分析

图4(a)(b)(c)(d)描述了当L分别取1D（108 mm）、2D(316 mm)、5D(540 mm)、10D(1 080 mm)时弯管内的流体流动情况。从这4张图片可看出:直管段长度L取1D时流线最紊乱。随着直管段长度L的增加，流线趋于光顺，管道内流体质点的运动也随之趋于稳定，流场紊乱程度得到缓解。当L增大到10D时，弯管间直管道内的流线基本平行。此结果说明直管段长度L的增大有利于流体流动的稳定性，即长直管段具有整流作用。

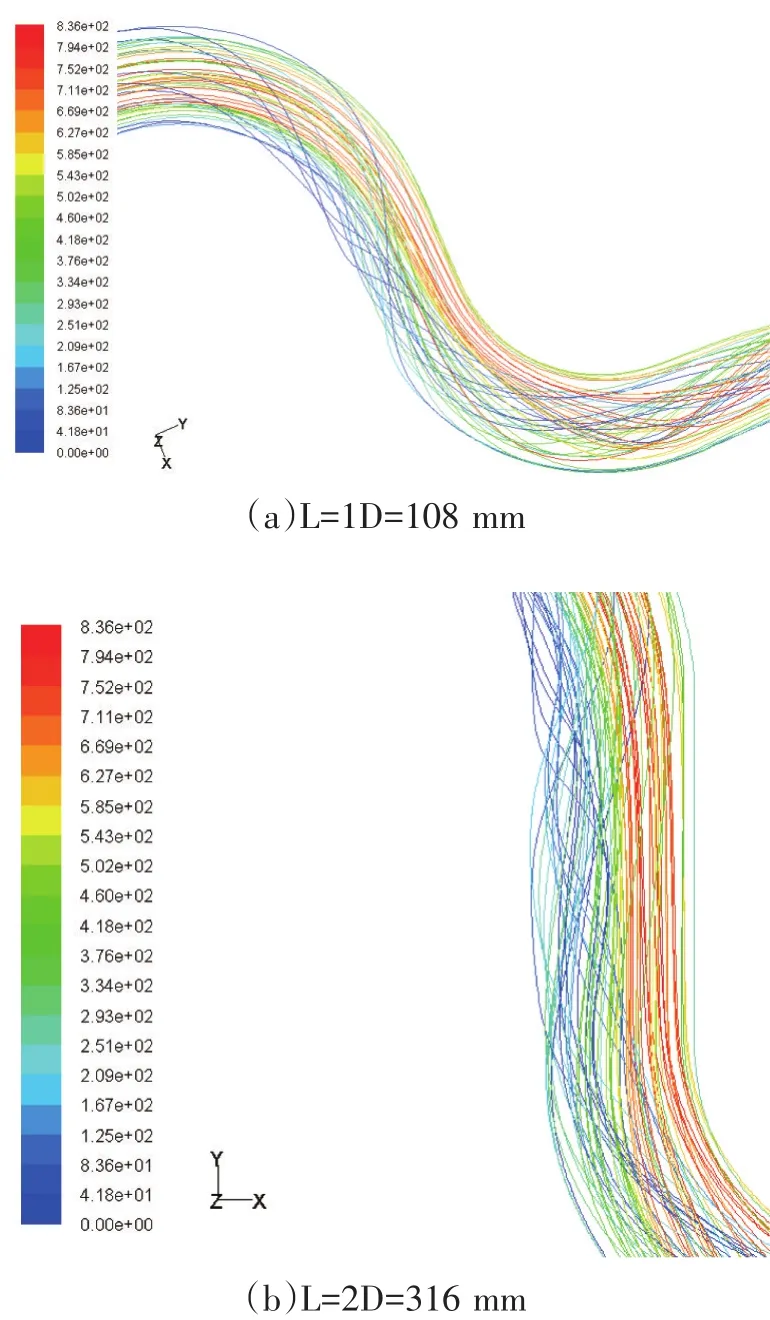
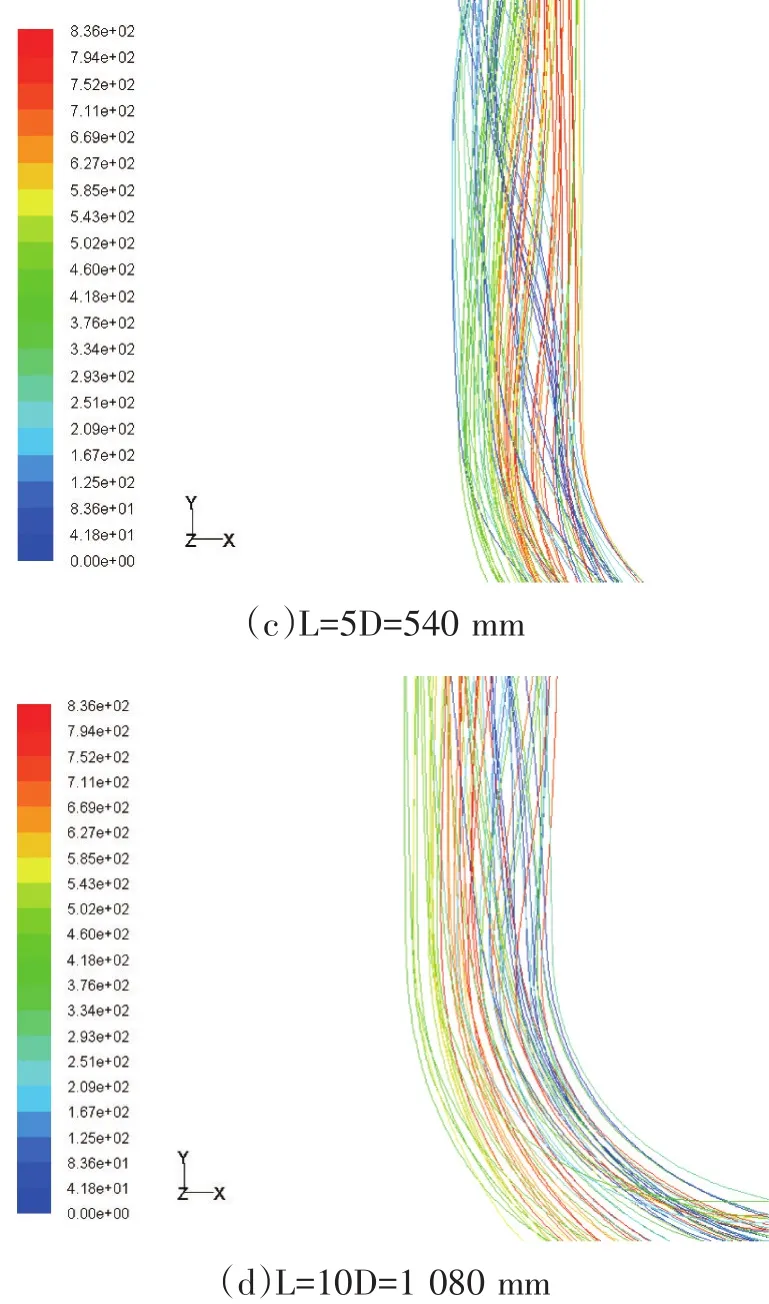
图4 不同直管道长度流线图

3.1.2 压力脉动分析

为了研究L对管内压力脉动的影响情况，取弯头处的监测面1和监测面2（监测面的布置如图1所示）进行压力监测。直接监测得到的压力脉动是时域图，经过傅里叶变换，得到频域内的压力频谱图。表1就是在L取不同数值时，两个监测面的脉动压力级差值。

表1 监测面的脉动压力

从表1中可以看出，直管段长度L从108 mm增大到1 080 mm，直管段两端监测面1、2之间的压力脉动总级差值从1.787 0 db增大到3.511 0 db，但每单位长度上的脉动压力总级差值从0.016 5 db/mm减小到0.003 3 db/mm。

可分析得到：随着L的增大，每单位长度上的压力脉动变小。即L的增大可以平缓流场压力脉动的剧烈程度，减轻流场紊乱度，有利于提高管内流体流动的稳定性。工程上可以采用增大弯头间的直管道长度来改善管内流场的流动特性。

3.2 弯头曲率R

为了研究弯头的主要几何结构参数——曲率半径R对管内流体流动特性的影响。取弯头1（弯头1见图1所示）结构进行分析。在其它参数不变前提下，分别对 R=1D=108 mm；R=2D=216 mm；R=5D=540 mm 3种不同情况进行数值模拟分析。

图5和图6分别是R取不同3种数值时管内流体的流线图和压力分布图。图5显示：管道入口直管段内流线比较光顺，几乎是平行的直线。在经过90°弯头时，流线发生了旋转。R=1D弯头处流线最紊乱，并出现二次流现象，R=2D的流线也比较乱，但较R=1D稍好。R=5D弯管弯头处流线最平滑，二次流消失。

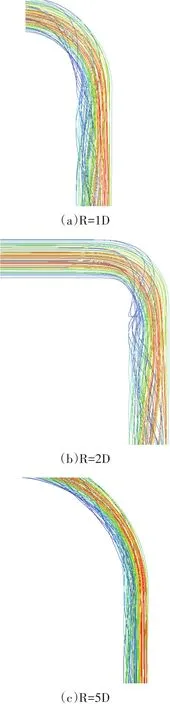
图5 不同弯头曲率半径流线图

从图6可看到，在弯头处，轴向的压力梯度很大，靠近内侧壁面区域的压力值较小，外侧壁面附近区域压力值较大。改变90°弯管的弯曲曲率半径，R的取值对弯头内部压力的分布几乎没有影响。

分析得到：弯管的曲率半径R的增大可以顺滑管道流线，稳定流体质点的运动，减轻流场紊乱度。

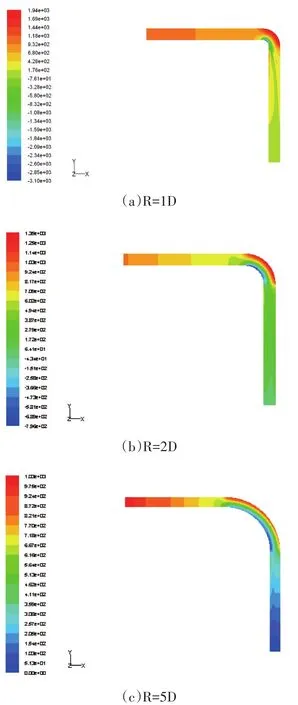
图6 不同弯头曲率半径压力分布

4 结论

4.1 研究了弯管结构对管道流体的流动特性的影响，直角圆弯管曲率半径R和弯管间的直管长度L越大，流体的流场越稳定。

4.2 弯管中弯头处流体的压力梯度最大，此处流线发生旋转，弯头是管道安全性能最薄弱的环节。

4.3 工程上可以通过采取增大曲率半径R、增加直管道长度L这两种措施来改进管道结构，以改善弯管内的流体流动特性。

（参考文献11篇，刊略，需者可函索）