圆坯连铸二冷制度研究

圆坯连铸二冷制度研究

张书岩，刘晓勇

(中钢设备有限公司，北京 100080)

摘要：根据R10.5 m弧形圆坯连铸机的现场实际情况，建立了圆坯凝固数学模型。用现场铸坯表面温度的测量数据，修正了模型中的传热系数，使模型计算更加准确。在此基础上，成功地开发了Φ400 mm圆坯连铸的二冷工艺制度并应用于实际生产。生产的钢种有20#、34Mn5V、26CrMo4等，其铸坯内部质量全部合格。

关键词：圆坯；凝固模型；二冷制度

中图分类号：TH164; TQ920.5文献标识码：A

收稿日期：2015-06-17；修订日期：2015-08-02

作者简介：张书岩(1981 - )，男，硕士，中钢设备有限公司工程师。

Study on secondary cooling system for round bloom CC

ZHANG Shu-yan，LIU Xiao-yong

(Sinosteel Equipment & Engineering Co., Ltd., Beijing 100080, China)

Abstract：In this paper, according to actual situation of round billet caster (R10.5), the solidification mathematical model is built. By measuring surface temperature of strand on the site, the heat transfer coefficient of model is modified, which makes the model calculating result more accurate. On this basis, the secondary cooling system of 400mm round billet caster is successfully developed and applied to actual production. The production of steel 20#, 34Mn5V, 26CrMo4 etc.， the internal quality of round billet is qualified.

Keywords：round billet; solidification model; secondary cooling system

0前言

圆坯连铸机的弧形半径为R10.5 m，冶金长度为31.5 m。浇铸圆坯的最大直径为350 mm[1]。为了适应市场的需求，拟在铸机上生产Φ400 mm的圆坯。原有的二冷配水制度没有Φ400 mm的冷却水表。为此，本文将建立圆坯连铸机的凝固模型，然后制定铸坯表面的目标温度并通过现场测定的温度数据对模型进行修正，最后利用开发的凝固模型制定Φ400 mm圆坯连铸的二冷配水制度。

1圆坯连铸凝固模型

根据圆坯连铸机特点，对圆坯面中心纵向截面(如图1所示)进行一些简化处理[2-5]，建立描述圆坯凝固传热的数学模型，然后进行温度场计算和凝固分析。

图1　计算区域 Fig.1　Computational region

描述圆坯凝固传热的微分方程

(1)

式中，T为温度，℃；ρ为密度，kg/m3；cp为热容，kJ/(kg·℃)；keff为有效导热系数，W/m；s0为源项。

对时间项采用隐式积分，则可得如下离散方程[6]

(Ap-SU)Tp=AWTW+AETE+SC

(2)

对于离散方程式中的源项

SC=DPTPOLD，SU=-DP,DP=ρCpVP/δt

(1) 初始条件。t=0时，结晶器中钢水温度等于浇铸温度，即

T(x, 0)=TC

(3)

(2) 边界条件[7]。

圆坯结晶器：

(4)

圆坯二冷区：

σε[(T+298)4-(Text+298)4]

(5)

铸坯中心：

(6)

2圆坯二次冷却水量的制定

二次冷却水量是根据铸坯目标表面温度来设定的，而目标表面温度则由浇铸工艺、钢种特性等参数确定。其最终目的是获得表面质量好、无缺陷的铸坯。

2.1圆坯目标表面温度

铸坯目标表面温度的确定应综合考虑多方面因素[8-10]：(1)符合铸坯凝固传热规律，不能出现过大的温降或回温；(2)避开钢的低温脆性区。

根据典型钢种(20#、26CrMo4、34Mn5V)的高温热塑性能，将其分成三类，然后确定浇铸Φ400mm圆坯的目标表面温度见表1。

表1　铸坯目标表面温度分布

2.2凝固模型的验证

在计算铸坯沿铸机长度方向温度分布及坯壳厚度时，二冷段各冷却区的平均换热系数选取按如下关系式[11]：

Ⅰ区内弧：h=0.3496×W0.2898

(7)

Ⅱ区内弧：h=0.2951×W0.3912

(8)

Ⅲ区内弧：h=0.2301×W0.4675

(9)

Ⅳ区内弧：h=0.1817×W0.4675

(10)

式中，h为各冷却区的平均换热系数，kW/m2·℃；W为各冷却区单位面积的喷水量，L/m2·s。

图2和图3分别为Φ310 mm和Φ400 mm圆坯温度分布曲线，实际生产中铸坯表面温度的实测值也在图中标出。结果表明，本文所建立的模型是合理的，可以准确地计算出铸坯的温度分布。

图2　圆坯直径Φ310 mm、钢种20#的 模型计算值与测量值比较 Fig.2　Comparison between calculation and measurement value (Round billet diameter 310mm, steel 20#)

图3　圆坯直径Φ400mm、钢种34Mn5V的 模型计算值与测量值比较 Fig.3　Comparison between calculation and measurement value (Round billet diameter 400mm, steel 34Mn5V)

2.3二次冷却水量的制定

依据铸坯的目标表面温度、喷嘴的实际喷水能力以及铸机工艺参数，来确定二次冷却水量。利用二分法思想[12, 13]，在计算程序中专门编制了目标水量反算子程序。目标水量反算子程序计算的结果如图4～7所示，图中浇铸条件为20#钢、过热度为30 ℃。由于是在原有的冷却条件下增加浇铸断面，当拉速低于安全水量(喷嘴的最小水流量)所设定的最小拉速时，各区水量为安全水量、不随拉速变化。当高于最小拉速时，各区的水量与拉速呈线性或二次曲线关系，并随拉速增大而增加。图6和图7的曲线一致的原因是，III区、IV区使用的喷嘴是同一型号的喷嘴。

图4　铸坯二冷I区水量与拉速的关系 Fig.4　Relationship between water quantity and speed on secondary cooling I zone

图5　铸坯二冷II区水量与拉速的关系 Fig.5　Relationship between water quantity and speed on secondary cooling II zone

图6　铸坯二冷III区水量与拉速的关系 Fig.6　Relationship between water quantity and speed on secondary cooling III zone

图7　铸坯二冷IV区水量与拉速的关系 Fig.7　Relationship between water quantity and speed on secondary cooling IV zone

2.4计算实例

图8～11为20#钢铸坯温度和凝固坯壳厚度分布图：图8和图9的浇铸条件为拉速在0.4 m/min、浇铸温度在1 540 ℃，图10和图11为拉速在0.5 m/min、浇铸温度在1 540 ℃。结果表明计算的表面温度曲线基本与目标温度吻合。而图8中III区、IV区末端温度偏低的原因是由于水量大造成的，但这不影响现场生产。

图8　铸坯表面和中心温度分布曲线图 (V c=0.4 m/min) Fig.8　Temperature distribution chart of billet surface and center

图9　铸坯液相线和坯壳厚度曲线图 (V c=0.4 m/min) Fig.9　Billet liquidus and the billet shell thickness curve

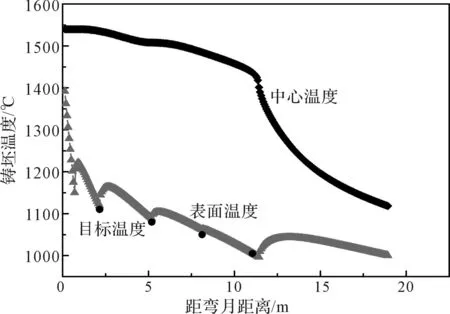
图10　铸坯表面和中心温度分布曲线图 (V c=0.5 m/min) Fig.10　Temperature distribution chart of billet surface and center

图11　铸坯液相线和坯壳厚度曲线图 (Vc=0.5m/min) Fig.11　The billet shell thickness and liquidus curve

3应用效果

20#圆坯4支Φ400 mm铸坯分别进行酸浸低倍分析，评级结果见表2。结果表明，芯部裂纹最高为1.5级、中部最高为0.5级、其余均为0级，符合标准要求。由于本次浇注Φ400 mm铸坯结晶器冷却强度偏大以及没有使用结晶器电磁搅拌，因此内弧柱状晶已达中心。铸坯酸浸低倍组织，柱状晶评为5级(一般为3级)；等轴晶率：本次试验(未使用结晶器电磁搅拌)为21.3%，而正常情况(使用结晶器电磁搅拌)为45%～50%。

表2　 Φ400 mm圆坯低倍酸浸检验结果

4结论

(1)根据圆坯铸机建立凝固模型，通过二冷区铸坯表面温度测定的数据修正后，可为圆坯连铸二次冷却水量的制定提供可靠依据。

(2)用上述凝固模型制定的Φ400 mm圆坯二次冷却水量表，成功浇铸出20#、34Mn5V、26CrMo4等钢种且内部质量合格的铸坯。

参考文献：

[1]陈超, 徐尚义, 景重阳等. 天津钢管公司圆坯连铸二冷系统的分析[J]. 天津冶金, 1994(4): 10-13.

[2]B.G. Thomas, Brimacombe Lecture. Modeling of the Continuous Casting of Steel Past, Present and Future [J]. 59th Electric Furnace Conf.， Pheonix, AZ, 2001, Iron and Steel Soc.， PP: 3-30.

[3]Lee Jung-Eui, Han Heung Nam, OH Kyu Hwan and Yoon Jong-Kyu, A fully coupled analysis of fluid flow, heat transfer and stress in continuous round billet casting[J]. ISIJ International, 1999, 39(5):435.

[4]Mizikar E A. Mathematical heat transfer model for Solidification of CC Steel Slab [J]. Trans. Met. SOC. AlME. 1967, 239: 1747-1753.

[5]Uehara M, Samarasekera I V, Brimacombe J K. Mathematics Modelling of Unbending of Continuously Cast Steel Slab [J]. lronmaking&Steelmaking, 1986, 13(3): 138-153.

[6]陶文栓. 数值传热学[M].西安：西安交通大学出版社，1995：27-29.

[7]闫小林. 连铸过程原理及数值模拟[M]. 石家庄：河北科学技术出版社，2001：61-70.

[8]朱立光，周建宏，王硕明等. 基于目标温度的方坯连铸二冷配水方案优化[J].炼钢，2006，(22)2：34-38.

[9]张克强. 连铸二冷区铸坯表面温度及配水研究[J].钢铁，2000，(9)：23-26.

[10]F.R.Camisani-Calzolari, I.K.Craig and P.C.Pistorius. Speed Disturbance Compenation in the Secondary Cooling Zone in Continuous Casting[J]. ISIJ, 2000,40(5): 469-477.

[11]赵克文，赵代琼，伍兵. 高效板坏连铸铸机的二冷技术[J]. 钢铁钒钛，1999(2):1-6.

[12]L. K. Chiang. Secondary Spray Cooling Study in the Continuous Casting of Stainless Steel Slabs[C]. Electric Furnace Conference Proceedings, 1999: 653-669.

[13]Hongming WANG, Guirong LI, Yucheng LEI. Mathematical Heat Transfer Model Research for the Improvement of Continuous Casting Slab Temperature[J]. ISIJ International, 2005,45(9): 1291-1296.