角三等分器的巧作
黄驹
摘 要 介绍角三等分器的结构、使用方法及制作原理。
关键词 初中数学;角三等分器;尺规
中图分类号:G633.63 文献标识码:B
文章编号:1671-489X(2015)21-0024-03
1 前言
初中数学人教版八年级上册“角平分线的性质”一节介绍了尺规二等分已知角的方法,学生学习以后往往提出如何三等分已知角?教材没有也不可能有尺规三等分已知角,用度量的方法三等分,学生虽然易学,但太乏味。为了迎合学生的求知欲,笔者制作了“角三等分器”,既能复习“等腰三角形的性质”,渗透“切线长定理”,又能激发学生的学习积极性。
2 简图结构及使用方法
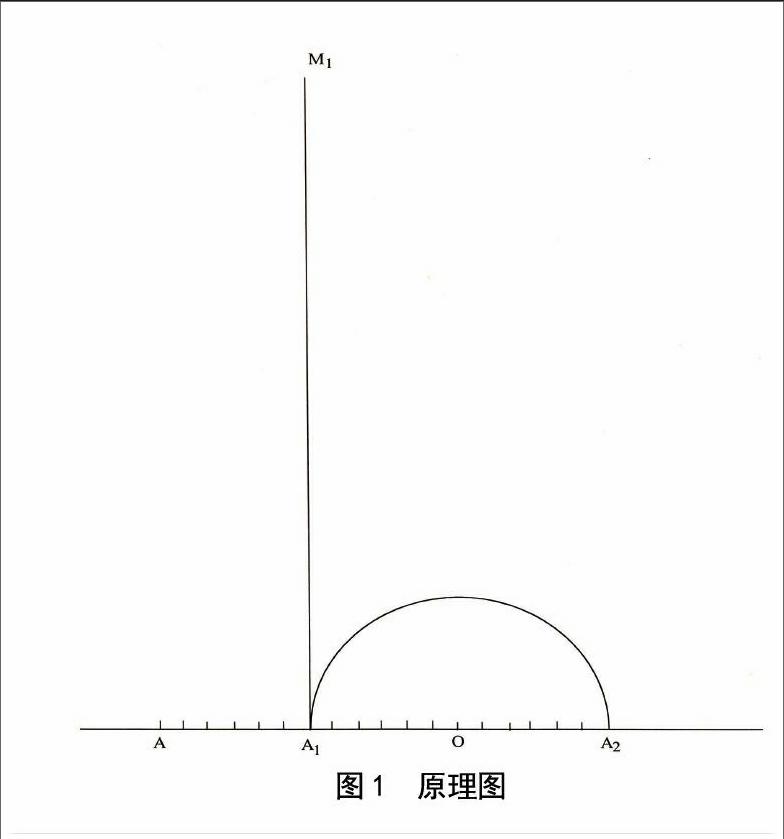
角三等分器的简图结构 如图1所示,线段A1M1垂直平分AO于点A1,A1A2是半圆O的直径,其中A1M1=30,AO=12。
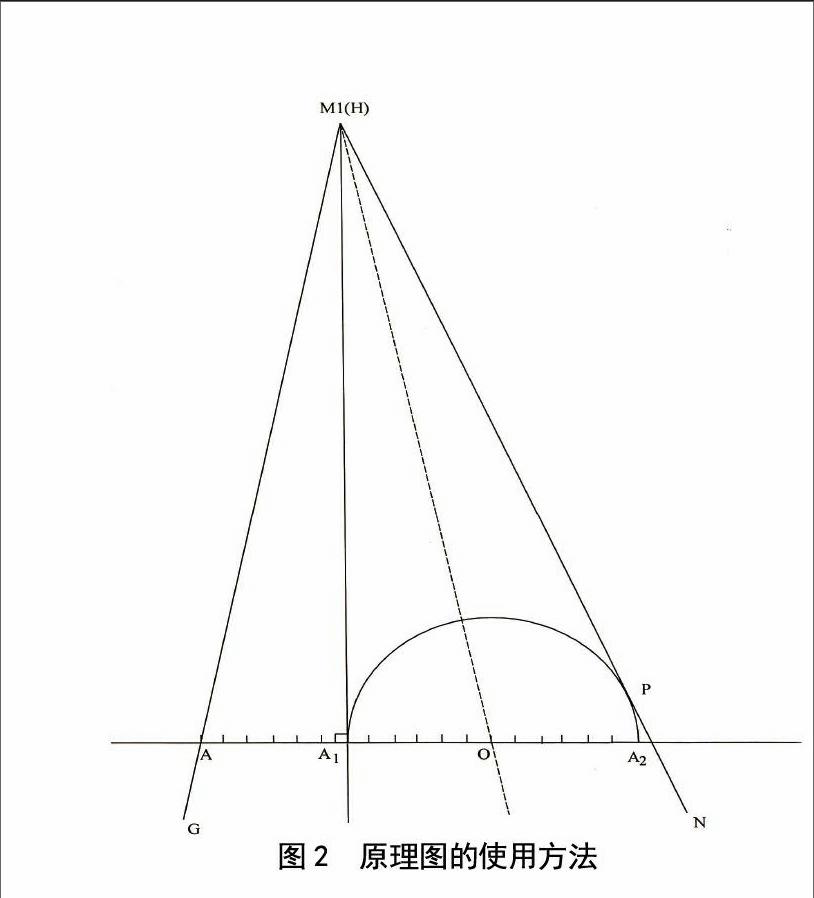
简图结构的使用方法 如图2所示,调节角三等分器与被三等分角之间同时满足“一切二过”,便能作出已知角的二条三等分线(以三等分已知∠GHN为例),步骤如下。
1)调节角三等分器的半圆与∠GHN的一边相切。(一切)
2)调节角三等分器,使线段A1M1经过角的顶点H(若角的边较长,可调节点M1与角的顶点H重合)。(一过)
3)调节角三等分器,使∠GHN的另一边HG经过点A。(二过)
4)分别记下点A与点O的位置。
5)分别作射线HA1和HO,则射线HA1和HO就是∠GHN的二条三等分线。
【注】此时利用了角三等分器的点A2(即利用过点A2的半圆)、O、A1(利用过点A1的垂线)和点A。为了便于利用图4三等分已知角,在此把A2、O、A1、A称为“第一组有效点”。
3 制作原理
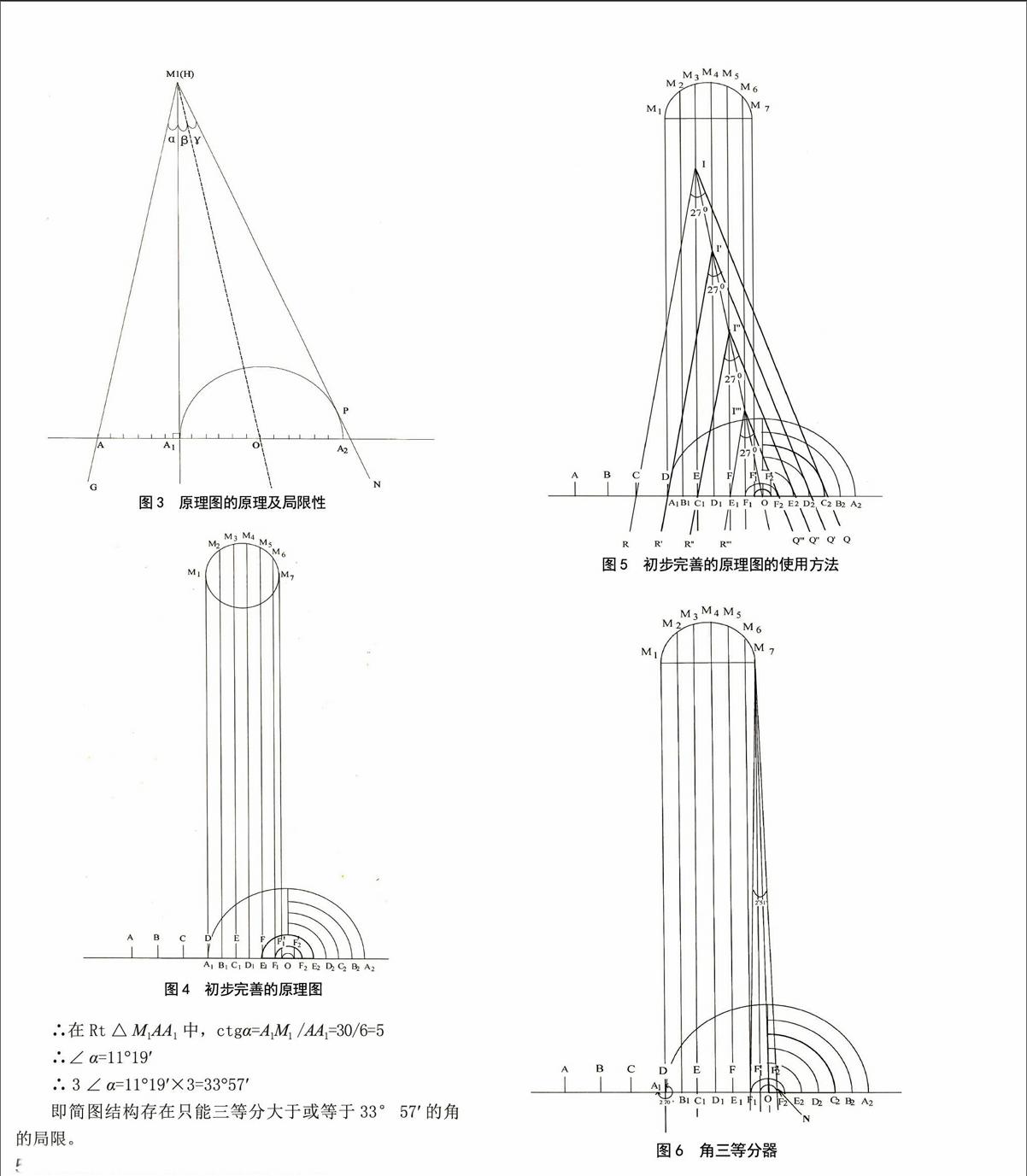
已知:如图3所示,△HAO中,HA=HO,HA1⊥AO于A1,半圆O分别切HA1和HN于A1、P。
求证:HA1、HO是∠GHN的二条三等分线。
证明:∵HA=HO,HA1⊥AO于A1
∴∠α=∠β(等腰三角形底边上的高平分顶角)
∵半圆O分别切HA1和HN于点A1、P
∴∠β=∠γ(切线长定理)
∴∠α=∠β=∠γ
即HA1、HO是∠GHN的二条三等分线。
4 简图结构的局限性
如图3所示,∵线段A1M1=30,而AA1=1/2·AO=1/2×12=6
∴在Rt△M1AA1中,ctgα=A1M1 /AA1=30/6=5
∴∠α=11°19′
∴3∠α=11°19′×3=33°57′
即简图结构存在只能三等分大于或等于33°57′的角的局限。
5 简图结构的完善制作及使用方法
简图结构的完善制作 如图4所示,为了能够三等分小于33°57′的角(且不用延长角的两边),必须对简图结构加以完善,完善制作过程如下。
1)作出半圆O的半径OA1的六等分点B1、C1、D1、E1、F1。
2)分别过点B1、C1、D1、E1和F1作OA1的垂线B1M2、C1M3、D1M4、E1M5和F1M6。
3)作半圆O的半径OA2的六等分点B2、C2、D2、E2和F2。
4)以O为圆心,分别以OB2、OC2、OD2、OE2和OF2为半径作出五个圆心角为直角的同心扇形,至此初步完善了角三等分器的结构,则:点B2、O、B1和B为第二组有效点;点C2、O、C1和C为第三组有效点;点D2、O、D1和D为第四组有效点;点E2、O、E1和E为第五组有效点;点F2、O、F1和F为第六组有效点。
不延长角的两边,利用三等分器三等分小于33°57′的角的方法 如图5所示,不延长角的两边,利用角三等分器三等分等于27°的∠RIQ。因为不延长角的两边,若利用简图结构(即利用第一组有效点A2、O、A1、A)三等分此角,显然无法同时满足“一切二过”,所以必须考虑利用第二组有效点(B2、O、B1、B)来三等分。容易发现利用第二组有效点仍无法同时满足“一切二过”,故改用第三组有效点(C2、O、C1、C)来三等分此角。步骤如下。
调节角三等分器,使过点C2的弧与角的一边IQ相切;使过点C1的垂线C1M3经过角的顶点I;使角的一边IR经过点C;记下点C1和O的位置;分别作射线IC1和IO,则IC1和IO就是∠RIQ的二条三等分线。
【注】∵线段DD2、EE2、FF2都小于CC2
∴利用第四组、第五组和第六组有效点均能三等分∠RIQ
增设第七组有效点能够三等分最小的角的度数为2°51′ 如图6所示,以O为圆心,以F1O为半径作小半圆O交F1F2于点F1和F2′,过点F1′作M7F1′⊥F1F2,则F2′、O、F1′、F1为第七组有效点。
过点M7作小半圆O的切线M7N,切点为N,连结M7F1得∠F1M7N,为被三等分的最小的角(射线M7F1′和M7O为二条角的三等分线)。
在Rt△F1F1′M7中,F1F1′=0.5,M7F1′=30
∴tg∠F1M7F1′=F1F1′/M7F1=0.5/30≈0.0167
∴∠F1M7F1′=57′
∴∠F1M7N=3∠F1M7F1′=3×57′=2°51′
被三等分角(θ)的取值范围 2°51′≤θ≤270°。endprint

