基于EMD和GA-BP神经网络的大坝变形预测
梁月吉,任 超,刘立龙,庞光锋,杨兴跃(桂林理工大学a.测绘地理信息学院; b.广西空间信息与测绘重点实验室,广西桂林 541004)
基于EMD和GA-BP神经网络的大坝变形预测
梁月吉,任超,刘立龙,庞光锋,杨兴跃
(桂林理工大学a.测绘地理信息学院; b.广西空间信息与测绘重点实验室,广西桂林541004)
摘要:提出一种基于经验模态分解( EMD)和遗传BP神经网络的大坝变形预测新算法。该算法首先通过EMD对变形序列进行分解,有效分离出非线性高频波动分量和低频趋势分量;然后应用遗传算法优化BP神经网络的权值和阈值,再对各分量进行建模预测;最后叠加各分量预测值得到预测结果。应用新算法与灰色GM ( 1,1)、回归模型、普通卡尔滤波和遗传BP神经网络算法进行对比分析。结果表明,该算法具有较强的自身内部环境优化和外部平台构建能力,自适应能力和非线性拟合能力较强,在一定程度上保证较优的局部预测值和较好的全局预测精度,在大坝变形预测中具有一定的实用价值。
关键词:大坝变形;经验模态分解;遗传算法; BP神经网络;精度评定
0 引言
由于大坝变形往往受诸多因子的影响,如温度、水位等,这些因子具有很强的随机性和难以解析的非线性,使得传统的预测方法在预测中不能很好地表达变形量与影响因素之间的复杂关系,难以得到准确、可靠的预测结果。高层建筑物变形实质就是一种随时间或空间变化的信号,那么,大坝变形分析也可以归为信号分析[1]。因此,王新洲等[2]将大坝不同时间段的位移值作为一时间序列,直接以大坝变形的历史监测数据来建模分析,模型排除影响大坝变形的因子,取得比较好的预测结果。近年来,随着非线性预测模型的不断发展,人工神经网络在时间序列建模中得到了较为广泛的应用[3],但传统的人工神经网络存在自身的一些不确定因素(如隐含层结点数的选取、训练函数的确定、初始连接权和阈值的选择等),而且容易陷入局部极小点、泛化能力不强或过于学习等。针对神经网络的缺点,研究者们提出了许多优化神经网络的方法,如粒子群算法、遗传算法、差异进化算法等,其中遗传算法( genetic algorithm,GA)具有较好的全局搜索能力,能有效提高神经网络自身性能[4]。这些优化方法虽然都进一步改善了神经网络的不足,但仅优化了神经的内部环境,对于非线性和随机性变化的大坝位移时间序列数据预测,仍存在一定的局限性。Murtagh等[5]提出了小波与神经网络相结合的“三阶段”策略,通过将变形时间序列分解成若干个子序列,再分别建立神经网络模型进行预测,得到比较好的预测效果。徐伟等[6]将小波分解与重构的原理用于大坝变形预测中,有效的将复杂信号分解为平稳信号,预测精度有了进一步提高。但是小波分析不具有自适应特点,往往是靠经验值来选取小波函数和分解尺度,这样不易达到信号的全局最优分解。
Huang等[7]于1998年提出了一种新的信号处理方法——经验模态分解( empirical mode decomposition,EMD)。该方法是一种自适应处理非线性和非平稳信号的自适应分解方法,不需要确定任何函数,直接对信号进行平稳化处理,能够有效的提取原信号的趋势项[8]。与小波分析相比,EMD具有计算更加简单、直观、基于经验和自适应的特点。目前,EMD已在GPS信号处理中得到了有效的验证[9]。罗飞雪等[10]证实EMD能够有效的将大坝变形序列分解成具有不同特征尺度的平稳窄带信号。基于上述研究,本文提出了基于经验模态分解( EMD)和遗传BP神经网络的大坝变形预测新算法,主要由两部分构成:基于EMD的BP神经网络外部平台构建和基于遗传算法的BP神经网络内部环境优化。该算法充分考虑了大坝变形的非平稳性、非线性和多尺度特征等特点,以及模型内部环境问题,通过EMD将大坝位移序列分解成一系列不同尺度特征的平稳信号,构建良好的外部平台;运用遗传算法优化BP神经网络的初始连接权值和阈值,再对各分量进行预测,最后叠加各分量得到预测结果。经算例验证,并与灰色GM( 1,1)、回归分析模型、普通卡尔滤波模型和遗传BP神经网络模型对比分析,证实新算法在大坝变形预测中是可行的,更具有优越性。
1 经验模态分解法
经验模态分解( EMD)是一种自适应信号分解方法,能够将存在于原始序列中不同特征的趋势逐级筛选出来,得到具有相同特征尺度的固有模态分量( intrinsic mode function,IMF),IMF必须同时满足两个条件[9]: 1)在待分解信号中,极值点的数目与过零点的数目相等,或最多相差1个; 2)在任一时间上,由局部极大值和局部极小值定义的包络均值为零。分解过程如下[7-9]:
①搜索出原始信号Y( t)的极值点,将所有的极大值点和极小值点用三次样条函数连接,即得到Y( t)的上包络线和下包络线,分别表示为Vmax( t) 和Vmin( t)。
②计算包络线的均值w1( t)

③计算信号Y( t)与包络线均值w1( t)的差值D( t)

④判断D( t)是否满足IMF的两个条件,如果D( t)满足条件,D( t)为信号Y( t)的第1个分量,即为L1;如果不满足条件,则把D( t)作为新的原始信号,重复执行以上步骤,直到满足条件为止。
⑤计算残差信号B1

⑥将B1作为原始数据,重复步骤①~③,不断分解出满足条件的Li,直到余量Bn是一个单调函数时,停止分解。此时,原始信号Y( t)可以表示为n个本征模态函数Li和1个余量Bn的和,即
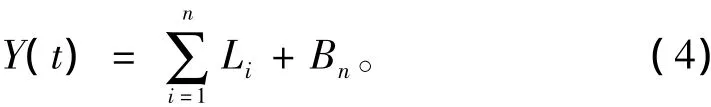
可见,经验模态分解相对于传统的小波分解算法减少了人为因素对分解结果造成影响,具有一定的优越性。
2 遗传算法优化BP神经网络
2. 1遗传算法
遗传算法( genetic algorithms,GA)是1962年由美国Michigan大学Holland教授提出的模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法[11]。该算法主要是选择的函数对输入种群的变量进行训练和优化,并通过对群体进行一系列的选择、交叉和变异筛选,得到适应度更好的个体,这样不断的优胜劣汰,使种群不断进化,最终得到全局最优解。
2. 2优化BP神经网络
神经网络方法是基于模仿人类大脑的结构和功能的一种新型信息处理算法。BP神经网络是神经网络算法之一,由Rumelhart等在1986年创立,它是基于多层前向神经采用误差反方向传播的学习算法进行权值调整,以得到拟合精度较高的神经网络[12]。
BP网络的设计,一般分为:输入转换层、输入层、隐含层、输出层输出转换层以及各层节点、传输函数、训练函数等,而网络的连接权值和阈值是神经网络的主要部分,直接关系到整个网络的性能和预测精度。因此,本文主要利用可在多个区域内寻求最优解的遗传算法优化BP神经网络各层之间的连接权和阈值,使BP神经网络预测效果更加稳定。
3 基于EMD和遗传BP神经网络的变形预测模型
3. 1本文模型预测步骤
对于本次大坝变形预测,计算步骤如下:
①学习和测试样本的确定,经EMD分解大坝时间序列Y( t),( t = 1,2,…,j)得到n个Li( i = 1,2,…,n)和1个余量B,则神经网络的输入样本为各个单一的Li或余量,输出样本是相应的分量Li或余量。为了减少模型误差的影响,所有的样本数据都要经过归一化处理,测试后再还原到原始区间。
②确定BP神经网络结构,本文设置的网络结构为输入层节点数为1、隐含层节点为3、输出层节点为1。设置种群结构体,并对权值和阈值进行编码,初始化种群参数,最大迭代次数为20,种群规模为5,交叉概率和变异概率分别为0. 3和0. 4。
③设计适应度函数,通过初始化种群参数网络训练后得到个体适应度函数,计算误差函数确定适应度函数值。一般情况下,误差大小和适应度成反比。
④进行选择、交叉、变异操作,产生新的种群,计算适应度,通过不断的迭代最终求解出最佳的初始化权值和阈值。
⑤学习样本的训练,BP神经网络输入层和隐含层之间采用Sigmoid函数,输出层采用线性函数,并计算学习精度和测试精度是否达到要求,如果达不到要求则返回步骤②~④,继续优化神经网络的初始化权值,直到预测精度满足要求为止。
⑥将训练好的神经网络进行大坝变形预测与分析,模型预测流程如图1所示。
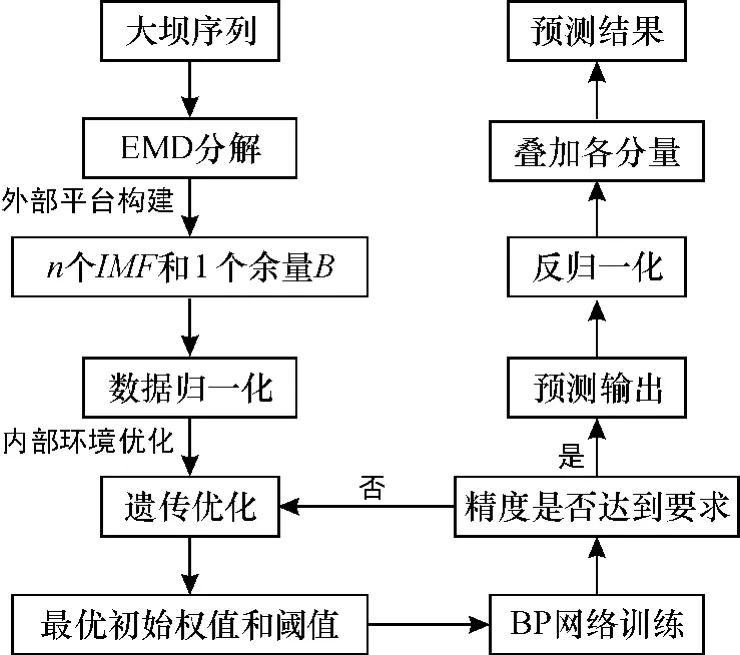
图1 模型预测流程Fig. 61Flow chart of prediction model
3. 2模型精度评定
为综合评定模型的精度,本文采用均方根误差和平均绝对值误差进行大坝变形预测模型的精度评定[13]。
1)均方根误差( RMSE)式中: Yt为大坝实际变形值;^Yt为大坝预测值; n为大坝观测期数; t为大坝观测第t期。
3. 3算例分析
本文以文献[14]大坝的0 + 119坝段的DC01监测点垂直位移变形监测数据为实验数据,观测时间( 1996年7月—1997年1月)跨度半年,观测频率为每月3次,垂直位移量是每次观测高程与第1次高程比较值。因此,采用该监测数据作为样本进行研究具有代表性(图2)。
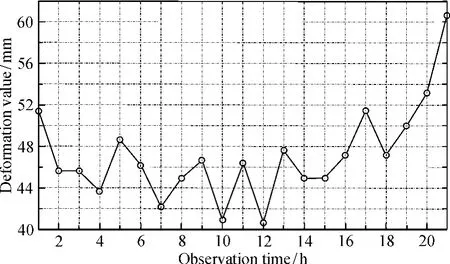
图2 大坝变形垂直位移序列Fig. 62Deformation of the dam vertical displacement sequence
可以看出,该大坝垂直位移变形极其不稳定,波动性比较大,呈非线性变化趋势。大坝变形第1 ~8期,体现出了大坝变形的特征;第9~12期的变动频率显示出具有一定的噪音特征,各期之间相差均为5. 75 mm;第13~21期的变形较为剧烈;而第18~21期的变形呈急剧上升趋势。该大坝变形的幅度变化较大,较为真实地反映了大坝的变形特征和变化趋势,最大变形值为60. 68 mm,最小值为40. 68 mm。可见,如果直接用传统的模型预测很难得到理想的结果。
因此,本文通过EMD将大坝序列分解为3个IMF和1个余量B (图3)。

图3 EMD多尺度分解Fig. 63EMD multi-scale decomposition
IMF1、IMF2、IMF3和B 4个分量的频率逐次递减,其中IMF1变形分量属于高频信号,IMF2和IMF3表现出大坝变形的周期性,B属于低频信号,代表大坝变形趋势。可见,经EMD分解后的大坝垂直位移变形子序列变化曲线比原始大坝变形序列曲线(图2)光滑,比较平稳,有利于变形分析与预报。
为了验证本文算法的可行性和优越性,建立5种方案进行算例分析比较:灰色GM( 1,1)预测模型(方案1)、回归分析预测模型(方案2)、普通卡尔滤波预测模型(方案3)、遗传BP神经网络预测模型(方案4)和基于EMD和遗传BP神经网络的预测模型(方案5)。方案1~4直接用原始数据进行建模预测;方案5通过以大坝序列的前11期为学习样本,后10期为预测样本来对EMD分解的各分量进行建模预测,最后叠加各分量。各IMF分量的预测结果和实际值对比见图4,各模型预测结果见表1,图5为各模型预测值和大坝实际值对比。

图4 EMD分解结果与预测值Fig. 64EMD decomposition results and the predictive values
由图4可看出:基于EMD和遗传BP神经网络的大坝变形预测模型对各分量的预测结果与实际值相符合。因此,经EMD分解得到的各分量,其物理特征更加明显,有利于方案5变形预测模型的建立和预报。
由表1可见:方案1和方案2的预测结果不稳定,部分预测值和实际值相差比较大,灰色GM ( 1,1)预测值的残差最大为-5. 664 mm,回归模型预测值的残差最大为3. 959 mm。方案3和4的预测结果比方案1和2好,普通卡尔滤波最大残差达到-3. 304 mm,遗传BP神经网络的最大残差为-1. 625 mm。而本文新算法的预测值和残差均优于其他预测模型,残差最小值为0. 000 mm,最大值仅为-0. 933 mm。从图4进一步看出:传统的灰色GM ( 1,1)和回归分析预测模型在预测中都出现了不同程度的波动,预测极其不稳定。普通卡尔滤波模型预测结果相对较好,遗传BP神经网络优于普通卡尔滤波模型,但这两种模型在大坝变形浮动大的第17~18期和第20~21期都有所波动。而新算法的预测结果接近于大坝实际值。可见,EMD能将隐含在大坝变形序列中的非线性高频波动成分和低频趋势成分分离出来,充分降低其非平稳性,为神经网络构建了良好的外部平台。同时运用遗传算法优化BP神经网络的初始连接权值和阈值,有效提高了整个网络的预测能力,在一定程度上保证了较优的局部预测值。
各模型精度分析见表2,图6为各模型的残差图。
灰色GM( 1,1)、回归分析模型和普通卡尔滤波模型的各项精度指标比较差,表明不能很好地反映大坝变形的演变规律。遗传BP神经网络的预测精度比传统的预测方法好,均方根误差为0. 267 mm。
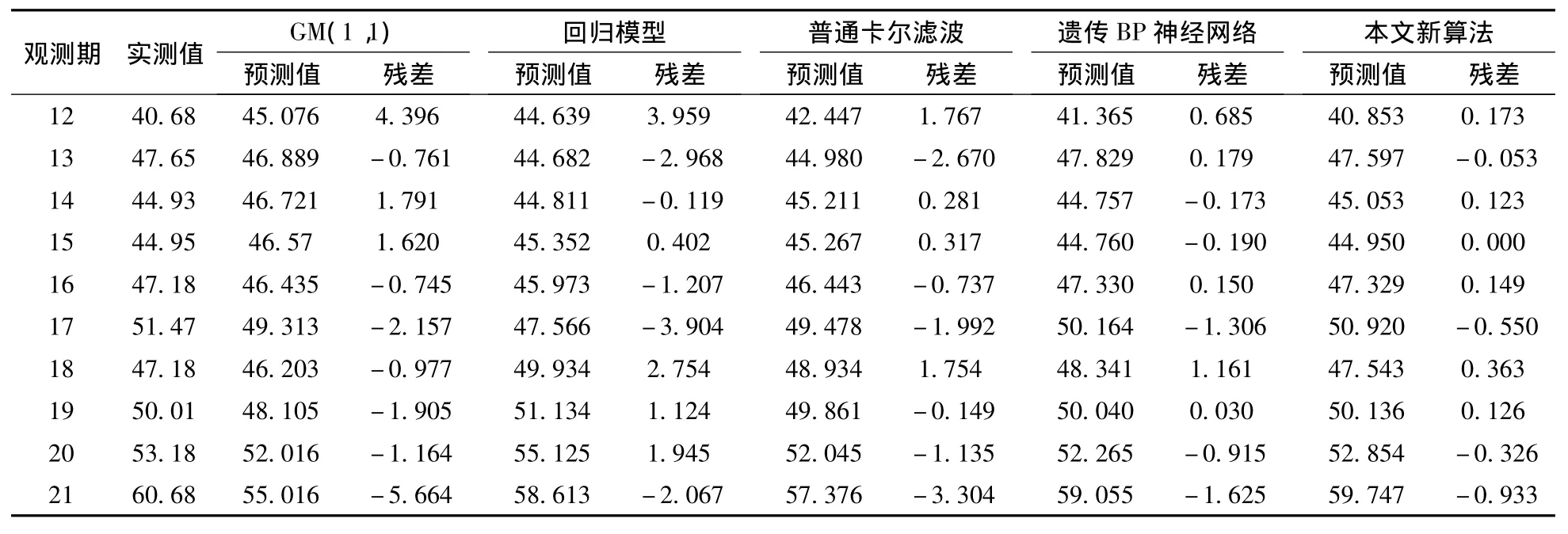
表1 各模型计算结果对比Table 1 Contrast of each model calculation results mm
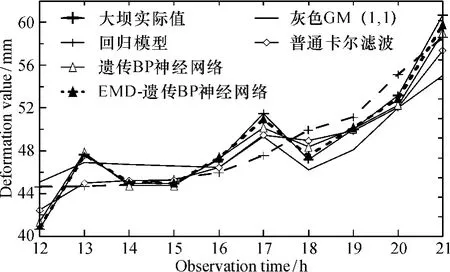
图5 各模型预测值和实际值对比Fig. 65Contrast of each model prediction and actual values
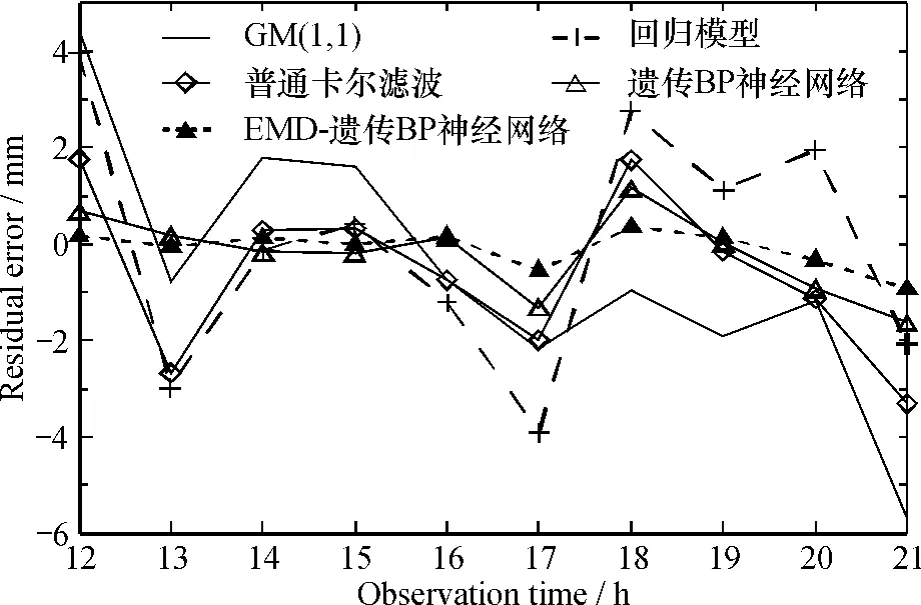
图6 各模型残差对比Fig. 66Contrast of model residuals

表2 各模型精度对比Table 2 Contrast of models precision mm
而本文算法的预测精度优于遗传BP神经网络,均方根误差和平均绝对误差分别为0. 122、0. 019 mm。可见,本文算法在一定程度上保证较好的全局预测精度,具有一定的优越性。从模型的残差曲线图(图6)进一步分析,灰色GM ( 1,1)、回归分析模型、普通卡尔滤波模型和遗传BP神经网络的残差变化较大,本文算法的残差曲线变化比较平稳。因此,利用EMD对大坝位移变形序列进行自适应分解,充分降低了序列的非平衡性,更体现出大坝变形的波动频率,有利于BP神经网络性能的充分发挥。同时,采用遗传算法优化后的BP神经网络进行预测,在一定程度上克服了传统神经网络存在的缺点,提高了BP神经网络的自适应和非线性拟合能力,预测结果更显示出大坝变形的变化趋势。
综上可见,基于EMD和遗传BP神经网络的新算法充分考虑了模型的内部环境优化和外部平台构建,无论预测结果还是预测精度都优于遗传BP神经网络和传统预测模型,该算法应用在大坝变形预测中是可行的,具有一定的优越性。
4 结论
在实际的大坝变形监测中,对大坝变形量分析和准确预测具有重要意义。本文将经验模态分解和遗传BP神经网络相结合应用到大坝变形预测中,经算例分析,并与灰色GM( 1,1)、回归模型、普通卡尔滤波和遗传BP神经网络对比表明:利用经验模态分解,能分离出隐含在时序中的非线性高频波动成分和低频趋势成分,这充分降低了大坝变形序列的非平稳性,为BP神经网络构造了良好的外部平台;采用遗传算法,改进了BP神经网络的性能,网络具有更强的自适应能力和非线性拟合能力;新算法在一定程度上保证了较优的局部预测值和较好的全局预测精度。因此,基于经验模态分解和遗传BP神经网络的新算法在大坝变形预测中具有一定的应用价值。
参考文献:
[1]马攀,孟令奎,文鸿雁.基于小波分析的Kalman滤波动态变形模型研究[J].武汉大学学报:信息科学版,2004,29 ( 4) : 349-353.
[2]王新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报:信息科学版,2008,33 ( 5) : 469-471.
[3]肖桂元,刘立龙.动态模糊神经网络在变形预测中的应用[J].桂林理工大学学报,2011,31 ( 3) : 395-398.
[4]刘勇健,李彰明,张建龙,等.基于遗传-神经网络的深基坑变形实时预报方法研究[J].岩石力学与工程学报,2004,23 ( 6) : 1010-1014.
[5]Aussem A,Murtagh F.Combining neural networks forecasts on wavelet-transformed time series[J].Connection Science,1997,9 ( 1) : 113-121.
[6]徐伟,何金平.基于多尺度小波分析的大坝变形自回归预测模型[J].武汉大学学报:工学版,2012,45 ( 3) : 285-289.
[7]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and Hilbert spectrum for non-linear and nonstationary time series analysis[J].Proc. R. Soc. Lond.A,doi: 10. 1098/rspa.1998.0193.
[8]张恒璟,程鹏飞.基于经验模式分解的CORS站高程时间序列分析[J].大地测量与地球动力学,2012,32 ( 3) : 129-134.
[9]戴吾蛟,丁晓利,朱建军,等.基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报,2006,35 ( 4) : 321-327.
[10]罗飞雪,戴吾蛟.小波分解与EMD在变形监测应用中的比较[J].大地测量与地球动力学,2010,30( 3) :137-141.
[11]谭华,韦林.遗传算法基本理论的仿真研究[J].计算机与现代化,2011 ( 1) : 6-10.
[12]张昊,王琪洁,朱建军,等.样本数据预处理对基于BP神经网络的GPS高程拟合的影响[J].大地测量与地球动力学,2011,31 ( 2) : 125-128.
[13]李潇,徐进军.动态稳健支持向量机在大坝变形预测中的应用[J].大地测量与地球动力学,2009,29 ( 2) : 118-120.
[14]万程辉,何习平.基于小波分析回归模型的大坝监测数据处理[J].测绘科学,2009,34 ( 5) : 113-115.
Dam deformation prediction based on EMD and GA-BP neural network
LIANG Yue-ji,REN Chao,LIU Li-long,PANG Guang-feng,YANG Xing-yue
( a. College of Geomatics and Geoinformation; b. Guangxi Key Laboratory of Spatial Information and Geomatics,Guilin U-niversity of Technology,Guilin 541004,China)
Abstract:A new algorithm based on EMD and genetic algorithm-BP neural network is proposed.First,to effectively separate the nonlinear trend of volatility of high frequency and low frequency components,the algorithm deformation sequence is decomposed by EMD.Then,genetic algorithm is used to optimize weights and threshold values of the BP neural network,to build a prediction model for each component.Finally,the predicted values of each component in the forecast is overlay.The calculation is analyzed and compared with grey GM ( 1,1),regression analysis,common Carl filtering and GA-BP neural network.The results show that the method can build external and internal environment optimization platform.With generalization ability and an adaptive fitting,it ensures the optimal local prediction with higher precision forecasting,and can be applied to dam deformation prediction practically.
Key words:dam deformation; empirical mode decomposition; genetic algorithm; BP neural network; precision evaluation
通讯作者:任超,博士,副教授,renchao@ glite. edu. cn。
作者简介:梁月吉( 1988—),男,硕士研究生,研究方向:变形监测与数据处理,1032271611@ qq. com。
基金项目:国家自然科学基金项目( 41071294) ;广西“八桂学者”专项经费项目;广西空间信息与测绘重点实验室项目(桂科能1207115-06) ;广西矿冶与环境科学实验中心项目( KH2012ZD0004)
收稿日期:2014-03-28
doi:10. 3969/j.issn. 1674-9057. 2015. 01. 017
文章编号:1674-9057( 2015) 01-0111-06
文献标志码:A
中图分类号:P258
引文格式:梁月吉,任超,刘立龙,等.基于EMD和GA-BP神经网络的大坝变形预测[J].桂林理工大学学报,2015,35 ( 1) : 111-116.

