岩体锚件轴向拔力计算
谢代兴,杨 杨,唐建生,潘晓东(中国地质科学院岩溶地质研究所/国土资源部、广西壮族自治区岩溶动力学重点实验室,广西桂林 541004)
岩体锚件轴向拔力计算
谢代兴,杨杨,唐建生,潘晓东
(中国地质科学院岩溶地质研究所/国土资源部、广西壮族自治区岩溶动力学重点实验室,广西桂林541004)
摘要:根据力的矢量平衡原理和工程情况,推导出不同角度斜拉状态下的岩体锚件轴向拔力基本式。采用预设参数法进行基本式验算和模拟斜拉状态下的岩体锚件抗拔试验,由试验结果和基本式函数图形分析出式中的平衡参数值,建立斜拉状况下岩体锚件轴向拔力计算式,用其计算岩体锚件不同角度的轴向拔力。该式可为岩体锚件(索、杆)工程、地灾治理中的牵引锚固工程、锚索锚固等工程设计和施工提供可供参考的计算依据,具有较好的应用价值和工程意义。
关键词:岩体锚件;轴向拔力;抗拔试验;计算方法;锚固
岩土工程锚固技术是当前岩土工程领域中的一个重要部分,发展前景喜人[1-3]。在岩土体地质灾害治理中,锚固技术得到了广泛的应用[4-6],取得了良好的经济效益和治理效果,同时,岩土锚固理论研究[7-13]也得到了进一步的发展。随着锚固技术在地质灾害治理方面应用的深入发展,锚固治理由直线型向折线型(如牵引固定法等,图1)发展的过程中,两种固定方法的母岩锚固段轴向拔(拉)力已发生了较大变化,在这种变化中,后者的锚固段轴向拔力计算方法目前尚未见相关报道,但这样的地质灾害治理工程已大量存在,如危岩体治理中的牵引固定法[14]、道路边坡的钢索(网)固定法、锚索工程[15]等。本研究主要针对不同角度斜拉状况下岩体锚件轴向拔力的计算方法与应用进行探讨,为斜拉状况下的岩体锚件轴向拔力计算提供一种可供设计和施工参考使用的计算方法。
1 岩体锚件抗拔破坏试验
1. 1试验部分
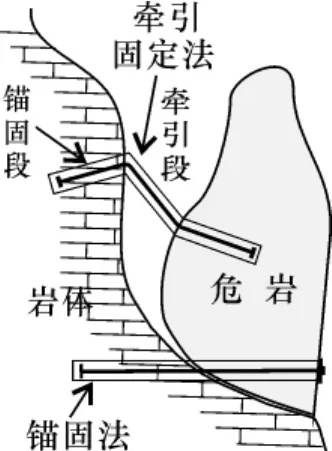
图1 锚固段轴向拔力分析Fig. 61Anchorage plan
试验材料:试验岩石为厚层坚硬的石灰岩,规格500 mm×400 mm×160 mm,抗压强度60~80 MPa;钢筋为Φ6 mm螺纹钢( HRB400),抗拉强度约17 kN,破坏试验拉力>30 kN;锚固剂为水泥砂浆V425水泥∶V石英砂∶V水=2∶1∶适量,终凝抗压强度18~20 MPa;试验孔径( D)为36 mm,锚固剂与孔壁的粘结强度( qs)取经验值1 500 kN/m2。
试验方法:采用室内抗拉试验方法进行;按β(斜向拉力( f)与锚件轴向拔力( F)之间的夹角) = 0°、45°、90°时不同长度锚件( L = F/π×D×qs)的抗拔破坏试验,试件共78件。
试验1:当β= 0°时,试验L = 90、100、110 mm的抗拉强度,试验共18件。
试验2:当β= 45°时,试验L = 80、75、70、65、60 mm时的抗拉强度,试验共30件。
试验3:当β= 90°时,试验L = 20、30、40、50、60 mm时的抗拉强度,试验共30件。
1. 2试验结果及分析
将β=0°、45°、90°时不同长度的岩体锚件锚固段抗拔破坏室内试验结果列于表1。
据试验结果分析:当β= 0°,L = 90 mm时锚件不稳定,L>100 mm时锚件稳定;当β=45°,L =60 mm时,锚件不稳定,L =65 mm时,锚件为临界稳定状态,L>70 mm时,锚件为稳定状态; 当β=90°,L = 20 mm时,锚件为不稳定状态,L =30 mm时,为临界稳定状态,L>30 mm时,锚件为稳定状态。
2 岩体锚件轴向拔力计算式
2. 1锚件轴向拔力的变化区间
试验结果表明:当β= 0°时,B = F = f(图2a) ;当β= 90°时,H = F = M×f(图2b) ;当β= 0°~90°时,F = f( 1~M) (图2c) ;由此确定F值的变化区间(定义域)为f≥F≥M×f。
2. 2轴向拔力基本式的推导
根据力的平衡原理将牵引拉力f受力图解(图2a)分析并由此引出式中: B为轴向分力。
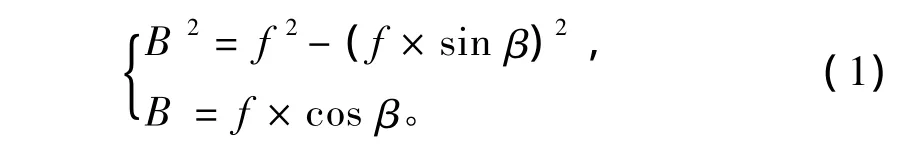
当β= 0°,式( 1)中B = F = f,推式成立,为直线型锚固法的轴向拔力;当β→90°时,B→0,当β = 90°时,B = 0,式( 1)不成立,应进行配式修正,修正的区间函数值为0~1。
试验证明,当β= 90°时,F = H = M×f,当β →0°时,H→0并与式( 1)互补,其互补配式应为与式( 1)相反的幂函数,据此有(图2b,推式略)
H = M×f( sin β)n。( 2)式中: H为轴向分力,n为正常数。
轴向拔力的基本计算式。当β= 0°~90°时,将式( 1)与式( 2)进行叠加,则有
F = f( cos β+ M( sin β)n)。( 3)
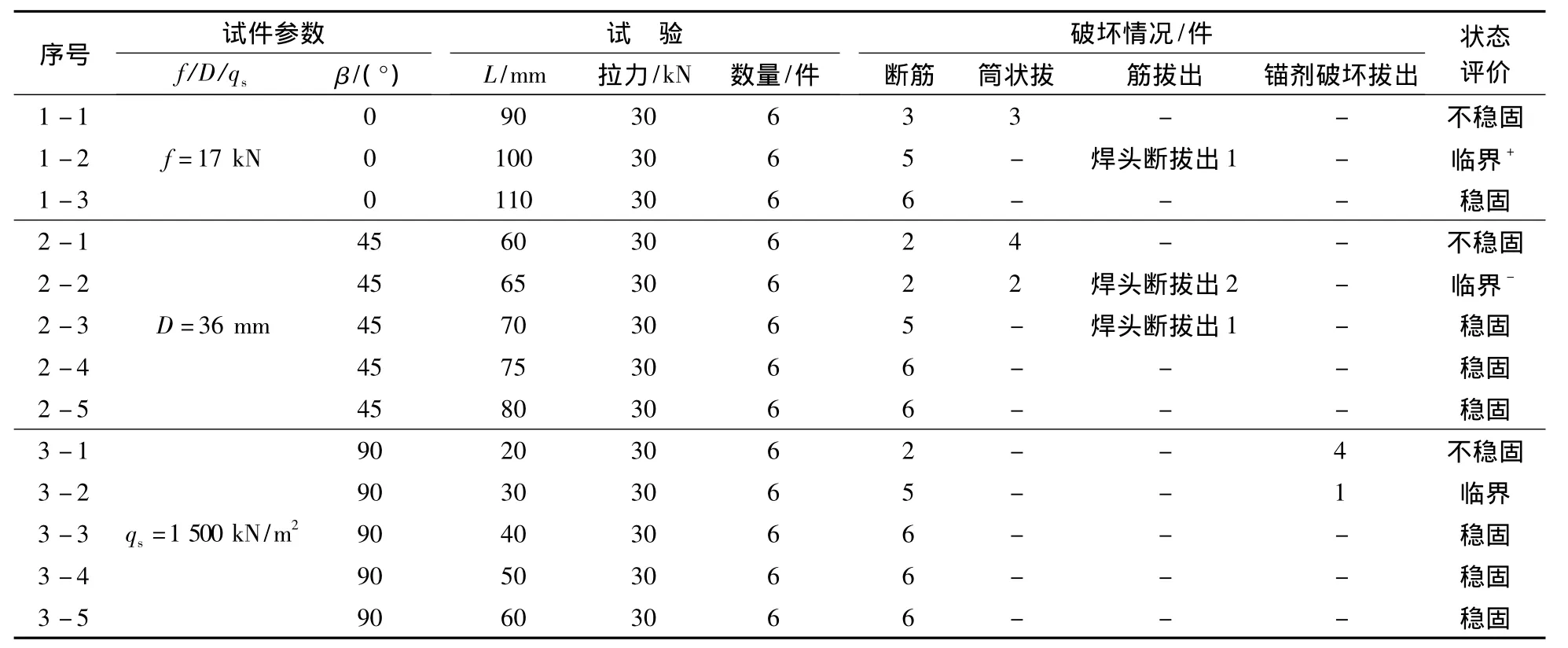
表1 石灰岩类抗拔试验结果Table 1 Pull-out test results of limestone
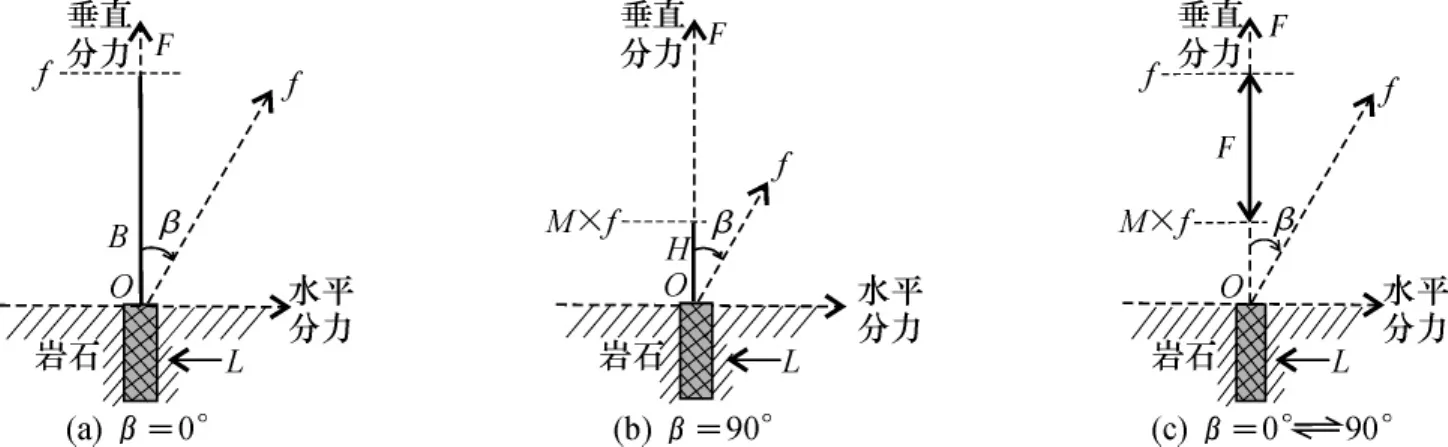
图2 β在不同角度锚固段轴向拔力分析Fig. 62Analysis of axial tension in anchorage with different β
2. 3轴向拔力计算式
2. 3. 1基本式中M、n值的确定M值:由表1试验结果分析后认为当β= 90°时,L = 30 mm为此试验的抗拔破坏的临界长度,此时的F值为0. 3f,因此取函数H中的M值为0. 3。
n值:采用图解方法(或验算法)求解常数n,其方法是作f = 17 kN,β= 0°~90°,n = 1~( n + 1)时的部分F = 17( cos β+ 0. 3( sin β)n)、B = 17 ×cos β、H = 5. 1( sin β)n曲线。对各曲线图形进行对比分析后认为:当n≤1及n>56时,F = f( cos β + 0. 3( sin β)n)函数不满足定义域f≥F≥M× f(图3a),计算式不成立;当n = 2~56时,F = f( cos β+ M( sin β)n)满足定义域f≥F≥M×f,计算式成立,但n值具有多选性,应进行作图分析,选择最佳n值;作n = 2~56时的F曲线,并通过F曲线中β= 20°、70°时的两点作向两端适当延伸的直线,以此直线为基线,靠近此线最近、线段最长时为最佳曲线,此时的n值为F函数最佳n值;经对比各曲线(图3)特征后认为n = 10时图形最佳,此时的曲线特征可大致分为β= 0°~20°段为曲线段,β= 20°~90°段为近直线段(图3f)。验算:当f = 17 kN、β= 45°、n = 10时,则F = 12. 13 kN、L值为71 mm;抗拔破坏试验结果证明L≥70 mm的锚固长度为安全锚固(表1)。综合权衡后认为: n = 10为F = f( cos β+ M( sin β)n)计算式的平衡常数值比较合适、安全;当n<10时则更趋向于安全状态。
2. 3. 2轴向拔力计算式将M = 0. 3,n = 10代入式( 3)后即为岩体锚件轴向拔力计算式,有
F = f( cos β+ 0. 3( sin β)10)。( 4)
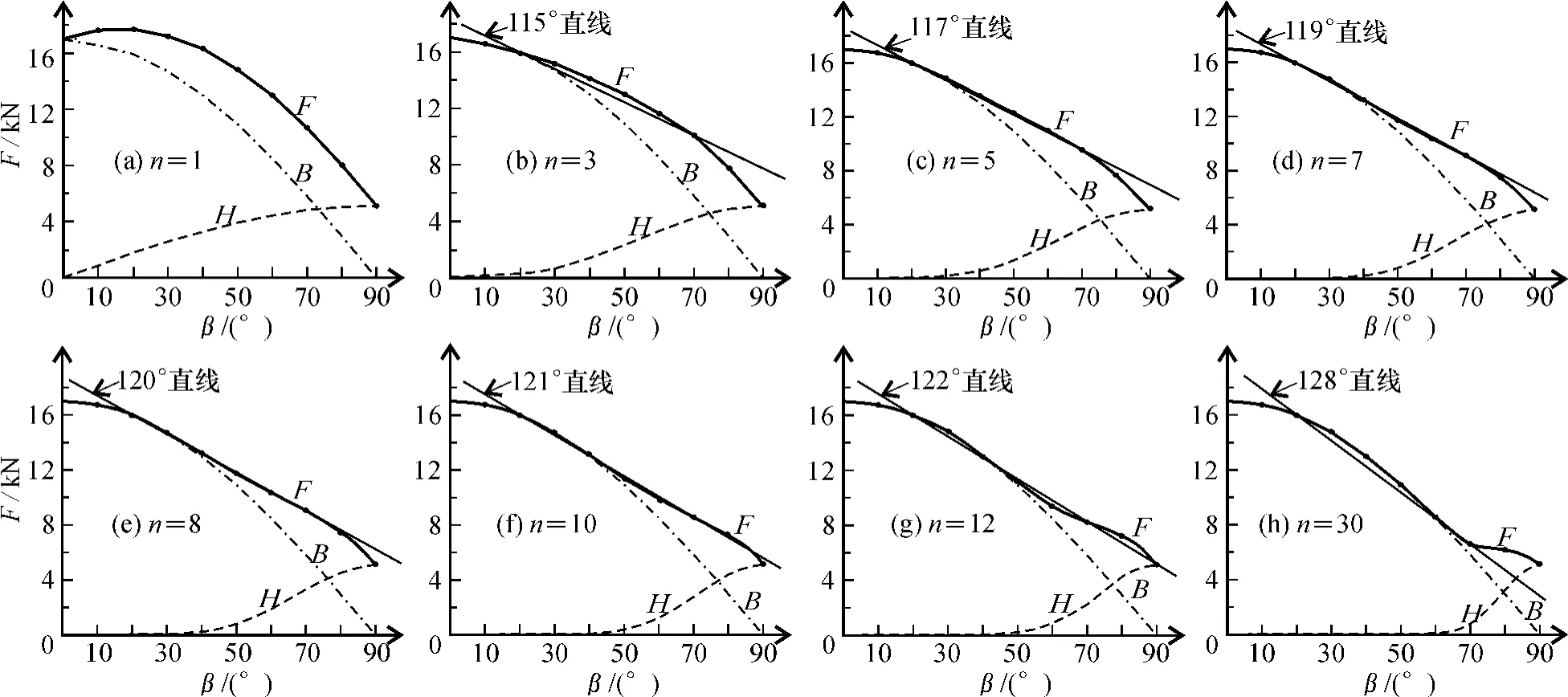
图3 牵引固定轴向拔力F曲线Fig. 63Curve of axial tension F in fixed traction
3 方法应用
3. 1工程应用实例
采用该方法计算岩体锚件的锚固段拔力,在桂林甑皮岩遗址独山危岩牵引锚固治理中广泛应用,治理危岩30余处,约1 500 m3;同时进了现场抗拔试验和危岩体治后长期观测,经2年变形监测,治后危岩体停止变形、岩体稳定,岩体锚件锚固段稳固,无变形,无裂迹;证实了该计算法可行,节约了大量治理经费,取得了较好的经济效益和治理效果。
3. 2锚件拔力函数表编制与应用
①函数表的编制。令Q = cos β+0. 3( sin β)10,则F = f( Q),当β= 0°~90°时,将每一β值与所对应的Q值列汇于表2。
②函数表使用方法。于工程设计和施工时首先确定斜向拉力值f,锚件与拉件的夹角β,查表中对应的Q值,再计算岀F值。如:设计钢索拉力f = 1 000 kN,钢索与锚件轴向夹角β= 60°,岩体锚件轴向拔力F = f( Q) = 1 000 kN×0. 571 2(查表2: β= 60°,对应的Q值为0. 571 2) = 571. 2 kN。
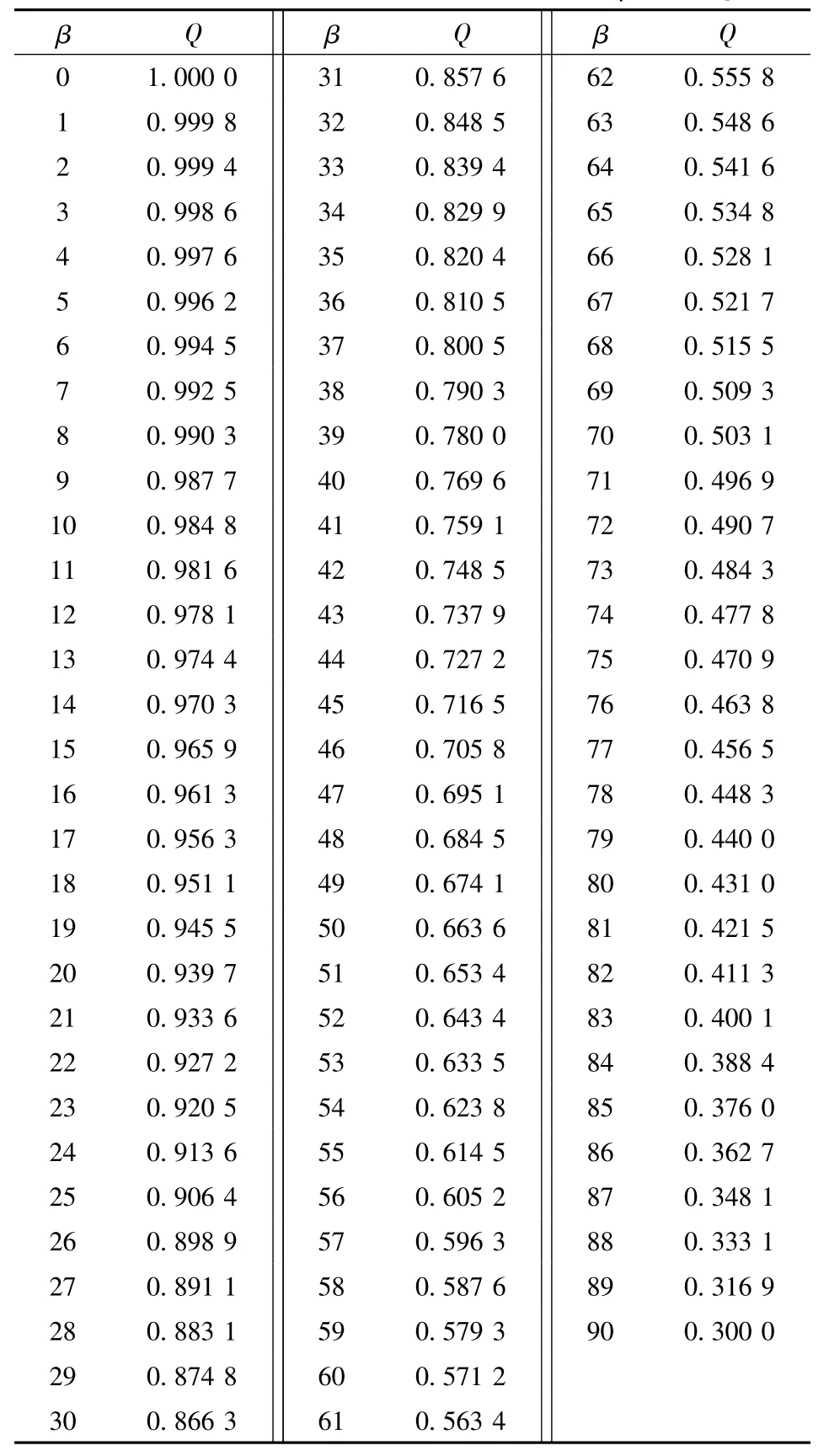
表2 β取不同值时的石灰岩类Q值( Q = cos β+0. 3 ( sin β)10 )Table 2 Q values of limestone type with diflerent β β/(°),Q/kN
4 结语与建议
( 1)通过对斜拉状态下岩体锚件轴向拔力的受力方式进行分析和模拟试验,建立起计算该类型的轴向拔力基本式,对基本式进行赋值验算和作图分析,析出基本式中的平衡系数,最终确定岩体锚件锚固段轴向拔力计算式为F = f( cos β+ 0. 3( sin β)10),计算式基本图形见图3f,当β= 0°~90°时所对应的Q = cos β+ 0. 3( sin β)10函数值见表2。
( 2)该方法可计算岩体锚件在不同斜拉角度时的锚固段轴向拔力,可为岩体抗拔锚桩工程、岩体牵引锚固治理工程、钢索牵引锚固工程等提供一种可供岩体锚件工程设计和施工参考的计算方法,具有较好的实际应用意义。目前因类似试验还尚少,可能存在不足之处,建议在引用该方法进行地质灾害等整治工程设计和施工时应进行必要的现场模拟抗拔试验,将M值调整到更接近当地情况后实施。
参考文献:
[1]张乐文,李术才.岩土锚固的现状与发展[J].岩石力学与工程学报,2003,22 ( S1) : 2214-2221.
[2]董学晟,邬爱清,郭熙灵.三峡工程岩石力学研究50年[J].岩石力学与工程学报,2008,27 ( 10) : 1945-1958.
[3]程良奎,韩军,张培文.岩土锚固工程的长期性能与安全评价[J].岩石力学与工程学报,2008,27 ( 5) : 865-872.
[4]刘世锋.预应力锚索在何群峡段危岩体整治工程中的应用[J].岩石力学与工程学报,2003,22 ( S2) : 2734-2737.
[5]康红普,王金华,林健.煤矿巷道锚杆支护应用实例分析[J].岩石力学与工程学报,2010,29 ( 4) : 649-664.
[6]刘波,李东阳,段艳芳,等.锚杆-砂浆界面黏结滑移关系的试验研究与破坏过程解析[J].岩石力学与工程学报,2011,30 ( S1) : 2790-2797.
[7]丁多文,白世伟,罗国煜.预应力锚索加固岩体的应力损失分析[J].工程地质学报,1995,3 ( 1) : 65-69.
[8]邓东平,李亮,罗强.预应力锚索加固土质边坡极限平衡稳定性分析[J].工程地质学报,2013,21 ( 1) : 53-60.
[9]李英勇,张思峰.岩土预应力锚固结构服役寿命研究[J].岩土力学,2012,33 ( 12) : 3704-3708.
[10]刘益,梅国雄,宋林辉,等.新型伞状抗拔锚的制作及其试验研究[J].岩石力学与工程学报,2009,28 ( S1) : 2935-2940.
[11]曾宪明,林大路,李世民,等.锚固类结构杆体临界锚固长度问题综合研究[J].岩石力学与工程学报,2009,28 ( S2) : 3609-3625.
[12]王清标,王以功,孙彦庆,等.不同岩性条件下预应力锚索锚固力损失规律研究[J].工程地质学报,2012,20 ( 5) : 849-854.
[13]马刚,周伟,常晓林,等.锚杆加固散粒体的作用机制研究[J].岩石力学与工程学报,2010,29 ( 8) : 1577 -1584.
[14]谢代兴,苏春田,周海.牵引固定法在危岩体治理中的应用[J].科技创业家,2013,7 (下) : 7-8.
[15]郭松峰,祁生文,李正熔,等.云南龙江特大悬索桥锚碇稳定性分析[J].工程地质学报,2011,19 ( 6) : 909 -916.
Calculation of axial pulling force in anchored rock
XIE Dai-xing,YANG Yang,TANG Jian-sheng,PAN Xiao-dong
( Institute of Karst Geology,Chinese Academy of Geological Sciences,Karst Dynamics Laboratory,Ministry of Land and Resources of Guangxi,Guilin 541004,China)
Abstract:According to the force vector balance principle and the engineering cases,the fundamental formula of axial pulling force in cable-stayed state with different angles of anchored rock was derived.The method of preset parameter was adopted to check the fundamental formula and to simulate the pull-out test of anchored rock in cable-stayed state.According to the test results and analyzed parameter values by the basic function graphic the state of cable-stayed calculating formula of axial pulling force of anchored rock is established.The formula can calculate the axial pulling force of anchored rock from different angles,providing useful reference for the project of anchored rock ( rope,rod),the traction anchoring engineering for the governance of geological disasters and the design and construction of anchor cable anchorage engineering.And the formula has good application and engineering significance.
Key words:anchored rock; axial tension; pull-out test; calculation method; anchoring
作者简介:谢代兴( 1957—),男,高级工程师,研究方向:水文地质、工程地质、环境地质,736570408@ qq. com。
基金项目:中国地质调查局地质调查项目( 1212010634803; 1212011220950; 12120114069001-01; 12120113052500)
收稿日期:2014-01-07
doi:10. 3969/j.issn. 1674-9057. 2015. 01. 011
文章编号:1674-9057( 2015) 01-0081-05
文献标志码:A
中图分类号:TU312
引文格式:谢代兴,杨杨,唐建生,等.岩体锚件轴向拔力计算[J].桂林理工大学学报,2015,35 ( 1) : 81-85.

