数据预处理对基于径向基函数网络高程转换的影响

黎峻宇，刘立龙，蔡成辉，林国标，黄良珂(桂林理工大学a.测绘地理信息学院; b.广西空间信息与测绘重点实验室; c.广西矿冶与环境科学实验中心，广西桂林　541004)



数据预处理对基于径向基函数网络高程转换的影响

黎峻宇a，b，刘立龙，蔡成辉a，b，林国标a，b，黄良珂a，b
(桂林理工大学a.测绘地理信息学院; b.广西空间信息与测绘重点实验室; c.广西矿冶与环境科学实验中心，广西桂林541004)

摘要:介绍了数据预处理对基于径向基函数网络的高程转换的必要性，提出了基于径向基函数网络高程转换建模的基本原理和实现步骤。结合工程实例，重点对归一化、中心化、标准化3种不同的数据预处理方法对基于径向基函数网络高程转换的影响进行计算分析。结果表明:针对大面积、高程异常值变化较大的区域，经过数据预处理后模型能够达到更高的转换精度;不同的预处理方法对转换结果影响不同，中心化预处理较其他两种方法能够更大程度地提高径向基函数网络高程转换的精度;归一化预处理方法不一定是最优的，进行高程转换前有必要对预处理方法进行选择。

关键词:归一化;中心化;标准化;数据预处理;径向基函数网络;高程转换;改善精度

当前，GPS测量技术已经在测绘生产实践中得到广泛应用，然而GPS测量直接获得的高是相对于WGS－84椭球面的大地高，实际生产过程中使用的却是相对于似大地水准面的正常高［1］。因此，为了使GPS测量技术能够得到更普遍的应用，必须将大地高H转换为正常高h，它们之间的关系是: h = H－ε，ε称为高程异常。故只需知道每一点的高程异常，就能够将该点大地高H转换为正常高h。高程异常转换方法主要有4类:几何解析法、物理大地测量法、人工智能法和混合转换法［2］。人工神经网络属于人工智能法的范畴［3］，近年来许多学者对人工神经网络高程转换模型作了进一步研究［4－14］，这些研究在一定程度上对高程转换模型进行了改进。然而，除了文献［3］进行了数据预处理对基于BP神经网络的高程转换的影响研究外，很少有人详细研究不同的数据预处理方法对高程转换结果的影响。径向基函数网络是一种结构简单、收敛速度快、能够逼近任意非线性函数网络，文献［1－2］中已经有一部分学者将径向基函数网络用于高程转换，并在一定程度上改善了高程转换的精度;然而进行高程转换的样本数据往往是相当庞大的，特别对于面积广、高程起伏较大的地区，样本数据中的信息很繁杂，且样本数据的北、东方向坐标不在一个数量级上，对数据进行预处理或许可以使得北、东坐标以及高程异常之间的关系挖掘过程更快捷、更精确，如此径向基函数才能更好地逼近北、东坐标与高程异常之间的函数关系。为了使得径向基函数网络在高程转换领域得到更好的发展，本文通过在严格的径向基函数网络结构基础上，增加一个数据预处理层，采用3种不同的预处理层构造3种不同的径向基函数网络模型进行高程转换，并将转换结果与不带数据预处理层的径向基函数网络模型的转换结果进行对比、分析，探讨数据预处理对基于径向基函数网络高程转换的影响。

1　基于径向基函数网络的高程转换方法

1. 1径向基函数网络基本原理

径向基函数网络是具有3层结构的前向网络:输入层在第1层，其节点个数等于输入向量的维数;第2层叫隐含层，节点个数由问题的复杂程度确定;第3层是输出层，节点个数等于输出数据的维数。径向基函数网络不同层的功能各不相同，隐含层是非线性的，以径向基函数为基函数，在此将输入向量空间转换到隐含层空间，达到将原来线性不分的问题变得线性可分的目的，输出层则是线性的［10］。一个严格的径向基函数网络结构如图1所示。

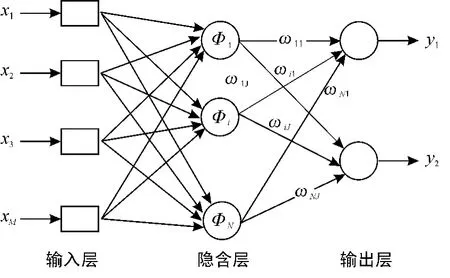
图1　严格的径向基函数网络结构Fig. 61Strict radial basis function network structure

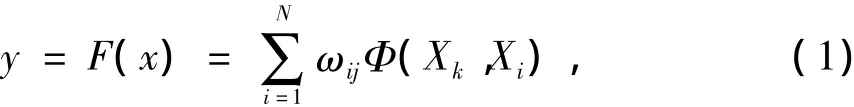
隐含层Φi( i = 1，2，…，N)为基函数，本文使用高斯函数为基函数，则有径向基函数网络模型为其中: Xk是m维的网络输入向量; y = F( x)为对应的输出;ωij( i = 1，2，…，N)为从第i个隐含节点到第j个输出节点的权值; N为隐含层神经元个数;是高斯函数基函数; Xi=［xi1，xi2，…，xim］为每个隐含层神经元基函数的中心;σi为拓展常数，且是所选取中心之间的最大距离，m为选取中心个数［1］;建立和训练一个严格的径向基函数网络，就是使其通过学习来确定Xi、ωi、σi的过程，以完成所需要的输入到输出的映射［2］。

1. 2径向基函数网络高程转换的实现

本文的径向基函数网络输入层神经元个数是2个，即控制点的平面坐标( x，y) ;输出层神经元个数为1个，即高程异常ε［1］。假设R = { ( Pi，Ti) | i = 1，2，…，M}为训练样本集，M为训练样本数，称P = ［P1，P2，…，PM］T为样本输入阵，其中Pi= ( xi，yi)，相应的教师输出为T =［T1，T2，…，TM］T，其中

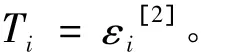
径向基函数网络的高程转换步骤为

①生成函数网络:本文中的径向基函数网络是通过MATLAB内的newrbe函数实现的，形式为net = newrbe ( P，T，goal)，P为样本输入阵，T为教师输出阵，均方差精度goal选用默认的微小值。

②调试网络:利用仿真函数Ts= sim ( net，P)对网络进行调试，net为①生成的函数网络，P为样本输入阵，将仿真输出Ts与T教师输出进行比较判断生成网络的可靠性，本文所生成网络满足可靠性要求(由文献［10］可知newrbe可以迅速创建一个误差为零的严格径向基函数网络)。

③高程转换:利用①中生成的函数网络，运用函数G = sim ( net，J)求验证样本点的高程异常，其中J = ( J1，J2，…，JN)T，Ji= ( xi，yi) ;输出阵G为利用径向基函数网络计算得到的高程异常阵，将G与正常高阵h = ( h1，h2，…，hN)相加就完成了所有点的高程转换。

2　数据预处理方法

数据预处理方法种类很多，适用范围也因实际处理问题的不同而不同。在高程转换相关文献中学者们最常用的方法是归一化、标准化，中心化也是比较经典的数据预处理方法，本文将就此3种数据预处理方法进行讨论。

将输入数据表示为Z = ( Z1，Z2)，Z1= ( x1，x2，…，xn)表示输入样本的北坐标矩阵，Z2= ( y1，y2，…，yn)表示输入样本的东坐标矩阵。

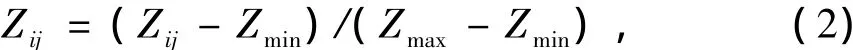
归一化公式为式中:Zij为样本数据Zij归一化的结果，Zmax、Zmin分别为Z1、Z2中的最大值和最小值［3］。

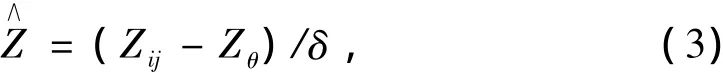
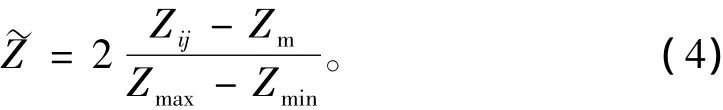
3　模型建立与实例分析

3. 1建立模型

本文在严格的径向基函数网络结构基础上，于输入层前分别增加1个归一化、标准化、中心化数据预处理层，构成3种不同的径向基函数网络训练方法来建立模型，分别简称归一化模型、标准化模型、中心化模型。实验过程中，运用这3种不同的模型和严格的径向基函数网络结构(无数据预处理层，在此称径向基模型)用同样的样本进行训练，并对相同验证样本进行高程转换［11］。

3. 2数据来源

采用某大型工程的D级GPS控制网点作为样本数据，该控制网共有点23个，控制区域面积较大，达850 km2。水准按照二等水准测量要求施测，高程异常变化较大，异常值变化如图2所示，其中坐标、异常值已通过归一化。取18个分布相对均匀的点作为训练样本，5个点作为验证样本［12－13］。样本数据点位分布见图3。

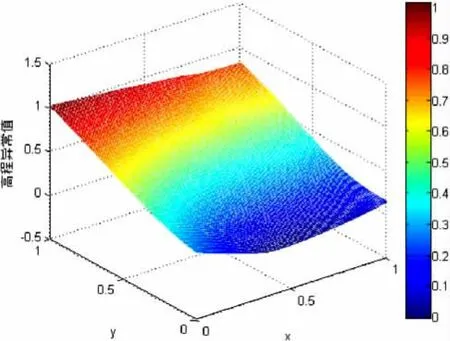
图2　异常值变化Fig. 62Change of elevation anomaly change

图3　样本数据点位分布Fig. 63Distribution of example points

3. 3模型精度分析

由文献［10］可知，newrbe可以迅速创建一个误差为零的严格的径向基函数网络，因此，不同的严格的径向基函数网络模型的可塑性都较好，在此不再就模型可塑性进行比较。本文通过比较不同模型转换所得高程异常与真值之差进行转换精度的评定，运用标准差来考察不同转换模型的泛化能力。比较统计见表1、图4。

标准差公式

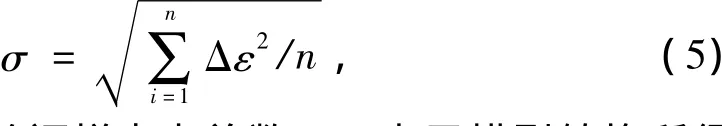
式中: n为验证样本点总数，Δε表示模型转换所得高程异常εi与高程异常真值ε之差。

本文实验区域中，数据预处理使得径向基函数

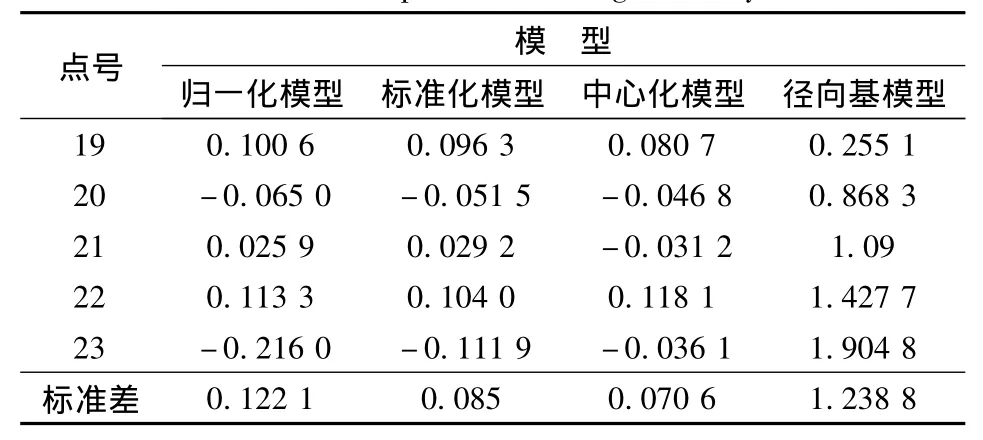
表1　转换精度比较Table 1　Comparison of fitting accuracy　m

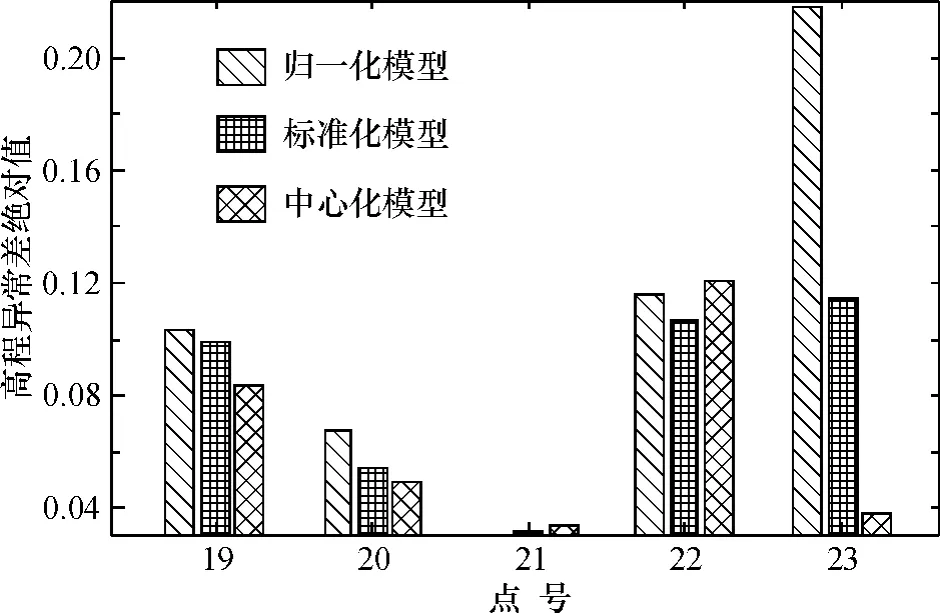
图4　不同模型转换结果误差绝对值Fig. 64Absolute value of fitting error based on different models

网络高程转换精度有较明显的提高，且大大改善了径向基函数网络模型的泛化能力。由此可见，在应用径向基函数网络进行高程转换时，对数据样本进行预处理是非常必要的。

由表1和图4得知，在本文实验中，中心化模型高程转换精度最高，几乎在所有验证点处的转换误差绝对值都是最小的，标准差最小，在3种模型中具有最强的泛化能力。标准化模型高程转换精度稍低于中心化模型，其各验证点转换误差接近于中心化模型，也具有一定的泛化能力。归一化模型高程转换精度较低，且在某些验证点处转换误差绝对值偏大，模型泛化能力较差。

4　结束语

本文通过对选定区域数据实验分析表明，针对大面积、高程异常值变化较大的区域，在3种预处理数据中，中心化预处理数据对径向基函数网络高程转换精度提高程度最大，中心化预处理与径向基函数网络结合的模型具有较强的泛化能力。一部分参考文献中常用的归一化预处理方法，可能不是提高高程转换精度的最优数据预处理方式。在进行高程转换时，有必要通过比较不同的数据预处理方法寻找更优的数据预处理方式，以达到更优化模型的目的。本文实验获取数据具有局域性，不同的数据预处理方式对其他高程转换模型以及在其他区域的优化能力有待进一步验证。

参考文献:

［1］刘建，王琪洁，王小辉，等．基于遗传算法的RBF神经网络在GPS高程转换中的应用［J］．测绘科学，2013，38 ( 2) : 143－145．

［2］任超，吴伟，黄征凯，等．基于AIC准则的RBF神经网络在GPS高程拟合中的应用［J］．测绘科学，2013，38 ( 2) : 77－79．

［3］张昊，王琪洁，朱建军，等．样本数据预处理对基于BP神经网络的GPS高程拟合的影响［J］．大地测量与地球动力学，2011，31 ( 2) : 125－128．

［4］王小辉，王琪洁，丁元兰，等．基于二次曲面和BP神经网络组合模型的GPS高程异常拟合［J］．大地测量与地球动力学，2012，32 ( 6) : 103－106．

［5］姬张建，袁运斌，盛传贞．混沌粒子群支持向量机并考虑地形改正的GPS高程拟合［J］．大地测量与地球动力学，2010，30 ( 2) : 95－98．

［6］焦明连，蒋廷臣．基于小波方法和Kriging估计的GPS高程转换［J］．大地测量与地球动力学，2008，28( 2) :100－103．

［7］魏子卿．GPS重力位水准［J］．大地测量与地球动力学，2007，27 ( 4) : 1－7．

［8］赵辉，张书毕，张秋昭．基于加权总体最小二乘法的GPS高程拟合［J］．大地测量与地球动力学，2011，31( 5) :88－91．

［9］孙传胜，杨国东，吴琼．神经网络在GPS高程拟合中的应用［J］．测绘通报，2011 ( 8) : 48－50．

［10］陈明．MATLAB神经网络原理与实例精解［M］．北京:清华大学出版社，2013．

［11］黄良珂，刘立龙，唐艳新，等．基于改进的Kriging法区域似大地水准面精华［J］．桂林理工大学学报，2012，32 ( 4) : 532－536．

［12］王新桥，黄良珂，刘立龙，等．GPS高程转换模型［J］．桂林理工大学学报，2013，33 ( 3) : 504－508．

［13］张腾旭，刘立龙，周淼，等．基于LS－SVM和BP神经网络组合模型的GPS高程拟合［J］．桂林理工大学学报，2014，34 ( 3) : 505－509．

［14］张腾旭，刘立龙，周淼，等．基于最小二乘配置法的高程拟合及精度评定方法［J］．桂林理工大学学报，2014，34(4) :728－731．

Effects of data pretreatment to elevation fitting on radial basis function network

LI Jun-yua，b，LIU Li-long，CAI Cheng-huia，b，LIN Guo-biaoa，b，HUANG Liang-kea，b
( a. College of Geomatics Engineering and Geoinformations; b. Guangxi key laboratory of Spatial Information and Geomatics; c. Guangxi Scientific Experiment Center of Mining，Metallurgy and Environment，Guilin University of Technology，Guilin 541004，China)

Abstract:The necessity of data pretreatment to the elevation fitting on radial basis function network modeling is described．The basic principle and implementation steps of the conversion modeling is depicted based on radial basis function networks elevation．With engineering examples，normalization，centralization，standardization of three different data pretreatment methods is used to calculate the impact of good conversion on radial basis function network．It is shown that data pretreatment model can achieve better conversion accuracy in a large area with elevation changes over the outliers．Different pretreatment methods result in different conversion．The centralization can improve the elevation accuracy on radial conversion function network in a greater degree．Normalization wouldn＇t be the best data pretreatment method．It is necessary for the selection of pretreatment method before elevation conversion．

Key words:normalization; centralization; standardization; pretreatment of data; radial basis function network; elevation fitting; raise accuracy

通讯作者:刘立龙，博士，教授，hn_liulilong@163. com。

作者简介:黎峻宇( 1989—)，男，硕士研究生，研究方向: GNSS技术及应用，lijunyu36@163. com。

基金项目:国家自然科学基金项目( 41064001) ;广西自然科学基金项目( 2012GXNSFAA053183; 2012GXNSFGA060001) ;广西研究生教育创新计划项目( YCSZ2013077) ;广西空间信息与测绘重点实验室项目(桂科能1207115－07) ;广西矿冶与环境科学实验中心项目( KH2012ZD004) ;广西“八桂学者”专项经费项目

收稿日期:2014－05－05

doi:10. 3969/j．issn. 1674－9057. 2015. 01. 015

文章编号:1674－9057( 2015) 01－0103－04

文献标志码:A

中图分类号:P228. 49

引文格式:黎峻宇，刘立龙，蔡成辉，等．数据预处理对基于径向基函数网络高程转换的影响［J］．桂林理工大学学报，2015，35 ( 1) : 103－106．