力学中一个趣味问题的讨论
力学中一个趣味问题的讨论
杨星宇
(北京师范大学物理学系北京100875)
摘 要:在3维空间和n维空间中,当一个质点受到某一确定质量和密度物体的最大引力时,对该连续分布物体的形状进行物理分析和数学运算可发现,当物体对质点有最大引力时,物体表面任意质量元对质点的引力在引力合力方向上的分量都相等,而且在3维空间中物体的形状并非球形.
关键词:万有引力定律n维空间最值问题物体形状
收稿日期:(2015-02-25)
对于3维空间中一个连续分布的物体,在质量和密度都保持不变的情况下,它具有什么样的形状时才会对一个质点产生最大的引力呢?会是球形吗?对于n维空间中的物体情况又如何呢?下面分别进行讨论.
1对3维空间中物体形状的讨论
1.1质点受力最大时 对物体形状定性讨论
若以质点所在位置为原点,质点所受引力合力的方向为极轴方向(即极角θ=0),建立球坐标系(r,θ,φ),其中r∈[0,+∞),θ∈[0,π],φ∈[0,2π),则物体上的任意一点可由坐标(r,θ,φ)确定,物体表面可由函数r=R(θ,φ)描述.
要使质点的受力最大,物体的形状应具有以下特性:
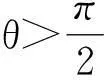
(2)物体形状具有旋转对称性,绕极轴旋转任意角度对称,故物体表面函数简化为r=R(θ)
“对称性原理”[1]:原因中的对称性必反映在结果中,即结果中的对称性至少有原因中的对称性那样多.由牛顿第三定律可知,物体对质点有最大引力时,质点对物体也有最大引力.现在考虑质点对物体的引力,由万有引力定律可知,质点产生的引力场以质点为球心成球对称分布.不妨设物体为流体,物体受质点引力场作用,考虑到特性1的要求,当其受力最大时,可知物体形状具有绕合力方向(即极轴方向)的旋转对称性.
1.2质点受力最大时 对物体形状定量计算
设该连续分布的物体质量为M,密度为ρ且都保持不变,质点的质量为m.
在球坐标系中,物体体积和质点所受引力合力的大小分别为
令
R1(cosθ)=R(θ)t=cosθ
可得
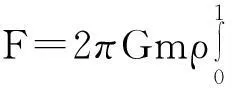
由变分法[2],解得
即
画出函数图像如图1所示,该曲线不是半圆.
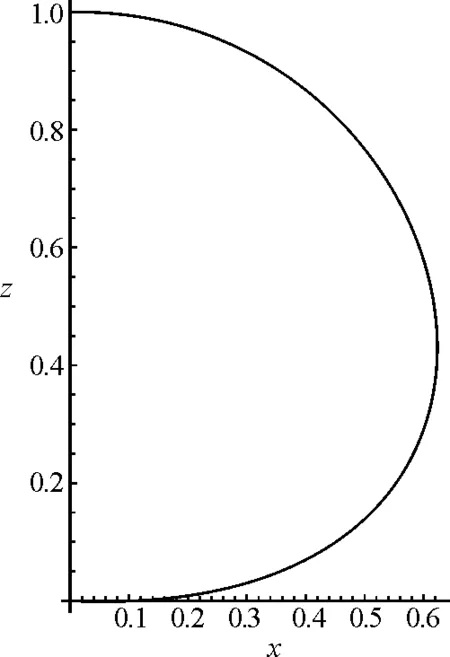
图1
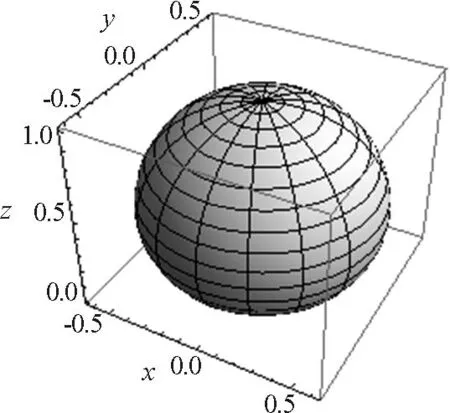
图2
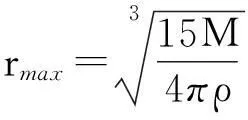
由对称性可知,引力合力方向沿极轴正方向.
2对n维空间中物体形状的讨论
2.1质点受力最大时 对物体形状定性讨论
以质点所在位置为原点,质点所受引力合力的方向为θ1=0所在轴(可称其为主轴)的正方向,建立n维超球坐标系[3](r,θ1,θ2,…,θn-2,φ),其中r∈[0,+∞),θi∈[0,π],φ∈[0,2π),故物体上任意一点可由n维坐标(r,θ1,θ2,…,θn-2,φ)确定,物体表面由函数r=R(θ1,θ2,…,θn-2,φ)描述.
与前文分析论述同理可得,要使质点的受力最大,物体的形状应具有以下特性:
(2)物体形状具有旋转对称性,绕主轴旋转任意角度对称,故物体表面函数简化为r=R(θ1).
2.2质点受力最大时 对物体形状定量计算
将万有引力公式推广到n维空间
设该连续分布的物体质量为M,密度为ρ,且都保持不变,质点的质量为m.
在n维超球坐标系中,物体体积和质点所受引力合力的大小分别为
其中dRnV为n维超球坐标系中的体积元
dRnV=rn-1sinn-2(θ1)sinn-3(θ2)…
sin(θn-2)drdθ1dθ2…dθn-2dφ
令
R1(cosθ1)=R(θ1)t=cosθ1
sin(θn-2)dθ2…dθn-2dφ
可得
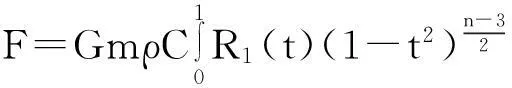
由变分法[2],解得
即
其中
此时,物体对质点有最大的引力.
3结论
3.1在3维空间中的结论
在3维空间中,物体对质点有最大引力时,物体表面在球坐标系中的函数表达式满足如下关系
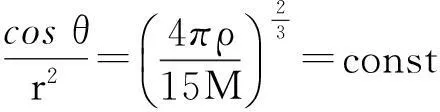
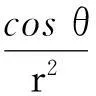
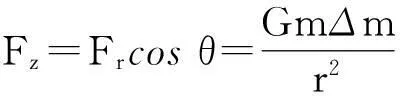
为常量,这表明,当物体对质点有最大引力时,物体表面任意质量元Δm对质点m的引力Fr在引力合力方向上的分量Fz都相等.
3.2在n维空间中的结论
在n维空间中,物体对质点有最大引力时,物体表面在n维超球坐标系中的函数表达式满足如下关系
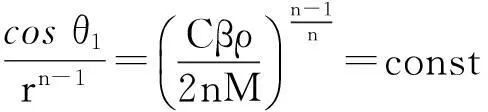
由上式可发现,当物体对质点有最大引力时,物体表面任意质量元对质点的引力在引力合力方向上的分量都相等.
3.3在2维空间中的结论
如果从n维空间退化到2维空间,那么当物体对质点有最大引力时,物体“表面”在平面极坐标系中的表达式满足如下关系
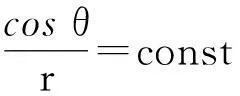
容易发现,上式就是极坐标系中圆的表达式.
故若物体是2维物体,物体对质点有最大引力时,物体的形状是“球形”,不过此球形是2维空间的球形,即圆.
参 考 文 献
1赵凯华.定性与半定量物理学.北京:高等教育出版社,1991.33
2欧斐君.变分法及其应用:物理、力学、工程中的经典建模.北京:高等教育出版社,2013.47~65
3StewartJ.Calculus:ConceptsandContexts[M].3rded.BROOKSCOLEPublishingCompany,2006:881
DiscussiononanInterestingMechanicalQuestion
YangXingyu
(DepartmentofPhysics,BeijingNormalUniversity,Beijing100875)
Abstract:Through physical analysis and mathematical operations on the shape of a continuous distribution object with constant mass and density in three-dimensional space and n-dimensional space respectively, find a conclusion: when the resultant gravity of the object on a given particle is maximal, the component of gravity on the given particle of any particle with euqal mass in the object′s surface in the direction of the resultant gravity is equal, and the shape of the object is not sphericity in three-dimensional space.
Keywords:thelawofuniversalgravitation;n-dimensionalspace;maximumorminimumproblem;objectshape

