基于分位自回归的中国人口死亡率动态预测
基于分位自回归的中国人口死亡率动态预测
赵明a,王晓军a,b
(中国人民大学 a.统计学院;b.应用统计科学研究中心,北京100872)
摘要:采用1994-2012年国家统计局公布的死亡率数据,针对Lee-Carter模型的预测方法提出改进,将分位自回归方法内置到Lee-Carter模型框架中,构建中国人口死亡率的分位自回归预测模型,对未来人口死亡率的变动趋势进行预测。通过与传统的均值回归方法比较,得出结论为:人口死亡率的分位自回归预测方法能够获取更加全面的信息,能够有效应对人类预期寿命被低估的可能,从而对未来死亡率的预测更加合理、可信。
关键词:分位自回归;人口死亡率;预测方法
中图分类号:C812∶C921文献标志码:A
收稿日期:2015-05-21;修复日期:2015-07-10
基金项目:国家自然科学
作者简介:唐吉洪,男,湖南祁阳人,博士生,研究方向:计量经济分析,宏观经济学;
一、引言
随着死亡率的降低,人口寿命延长成为必然趋势,从而对养老金系统的财务可持续性和人寿保险公司的经营稳定性造成影响。已有研究表明,国际权威机构对各国人口寿命延长趋势的预测结果往往低于实际水平,从而低估了人口寿命延长的不确定性即长寿风险对社会经济资源的冲击程度[1]。一个恰当、合理的死亡率预测方法将会有效应对人口寿命延长对社会经济实体带来的负面影响。
国内外关于死亡率模型的研究较多,最早的研究是由Lee和Carter 提出的动态死亡率建模方法,后人称之为Lee-Carter模型[2]。该模型假设死亡率由一个与年龄相关的截距项、与年龄相关且与时间有交互效应的斜率项以及一个时间趋势项构成。Lee-Carter模型具有参数少、拟合过程简单、预测结果稳定等优势,开创了动态死亡率预测的先河。然而,Lee-Carter模型也存在很多不足,国内外学者对此提出了很多改进,这些改进主要是针对模型的参数估计以及拟合优度问题。Wilmoth 针对Lee和Carter 在参数估计中使用的SVD方法进行改进,提出了加权二乘估计(WLS)方法和极大似然估计(MLE)方法,并运用日本1960—1990年的人口死亡率数据做了预测,参数估计的拟合优度较高,预测结果较好[3]38-59。Brouhns等提出了泊松对数双线性模型(PB模型),假设死亡人数服从泊松分布,放宽了残差项的同方差假设[4]。尽管学者们关于Lee-Carter模型参数估计和拟合优度问题的研究较多,但针对预测方法的探讨相对较少。Siu-hang Li和Waisum Chan在预测加拿大和美国人口死亡率的过程中,研究了时间序列中含有异常值情况的死亡率指数的发展趋势,通过对异常值的调整可以得到更好的拟合与预测效果[5]。在死亡率的预测方面,中国学者也做了大量的研究工作。李志生、刘恒甲采用1992—2007年中国人口死亡率数据进行研究,比较了不同的参数估计方法下死亡率的预测偏差,结果显示,加权最小二乘法下的参数估计值能够产生最小的死亡率预测偏差[6]。韩猛、王晓军采用PB模型,选取1994—2005年中国城市人口死亡率进行预测,模型的拟合优度较高,预测结果较为理想[7]。王晓军、任文东对有限数据下Lee-Carter模型在人口死亡率预测中的应用进行研究,在样本量较少时,对时间序列波动性进行研究,使得预测结果更加稳健与合理[8]。然而,在这些关于Lee-Carter模型预测方法的改进上,都没有脱离基于均值回归思想的时间序列预测方法。
本文针对Lee-Carter模型的预测方法提出改进,打破传统均值回归的预测方法,依据Koenker和Bassett提出的分位数回归方法,采用分位自回归模型(QAR模型)对时间序列进行预测[9]。QAR模型可以直接基于分位数回归方法进行参数估计,Koenker和Machado提出了分位数回归拟合优度的检验方法和QAR模型拟合优度的表示形式,Koenker和Xiao给出了模型参数估计的渐进分布,并提出了模型的一步预测和多步预测方法,这些学者的研究使得QAR模型在理论上得到充实[10-11]。另外,中国学者陈建宝和丁军军系统地对分位自回归方法进行了梳理,认为分位数自回归方法考虑更广泛条件下的一系列分位数函数,以度量条件异质性,与均值回归方法相比,其估计效果具有较好的稳健性[12]。因此,本文基于分位自回归方法,将该方法内置到Lee-Carter模型框架中,构建中国人口死亡率的分位自回归预测模型(QAR-Lee-Carter模型),对未来人口死亡率变动趋势和人口寿命进行预测,并与均值回归方法的预测结果进行比较,最后得出相应的结论与建议。
二、模型的建立
(一)Lee-Carter模型
Lee和Carter提出的模型框架为[2]:
lnmxt=αx+βxkt+εxt
(1)
其中,mxt为x岁的人在第t年的死亡率;αx表示不同年龄(或年龄组)的死亡率与年份t无关的部分;βx表示不同年龄(或年龄组)的死亡率与年份t的交互效应部分;kt衡量了死亡率随时间t的变化趋势;εxt表示误差项。
为了使模型得到唯一的解,Lee和Carter提出了模型的正态化条件,即:
∑tkt=0,∑xβx=1
(2)
根据正态化条件及模型本身的特征,国内外学者提出了多种关于Lee-Carter模型参数估计的方法,其中包括奇异值分解法(SVD)、最小二乘法(OLS)、加权最小二乘法以及泊松对数双线性模型法(Poisson Log-bilinear)等。李志生、刘恒甲采用中国人口死亡率数据,比较了不同的参数估计方法下死亡率的预测偏差,结果显示,加权最小二乘法下的参数估计值,能够产生最小的死亡率预测偏差[6]。因此,本文选取加权最小二乘法作为Lee-Carter模型框架的参数估计方法。具体参数估计步骤如下:
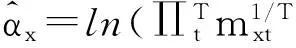
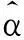
根据Wilmoth提出的加权最小二乘法,lnmxt的方差近似等于死亡人数dxt的倒数,采用dxt作为权重,得到加权的残差平方和为:
(3)
最小化公式(3)所示的加权残差平方和,可得:
(4)
通过以上步骤,便可以得到Lee-Carter模型的参数估计,接下来对kt建模。
(二)人口死亡率预测的分位自回归模型
1.模型的设定
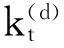
(5)
其中,Xt=(1,kt-1,kt-2,…,kt-p),θ(τ)=(θ0(τ),θ1(τ),…,θp(τ))′,ξt-1是由{k,s≤t}生成的σ-域。将式(5)中向量形式的参数展开,便可得到p阶的分位自回归模型:
(6)
其中,随机误差项εt服从i.i.d.。在式(6)中,如果将分位点τ固定,与普通的自回归模型十分相似。然而,普通的自回归模型是基于均值回归得到的结果,本文所建模型则是基于不同分位点进行回归,因此人口死亡率预测的分位自回归模型的参数估计、诊断与检验等方法与普通自回归模型之间存在差异。
2.参数估计
对于人口死亡率预测的分位自回归模型的参数估计,可直接基于Koenker和Bassett的分位数回归方法[9],通过求解如下最优化问题,得到τ分位点处参数的估计值:
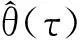
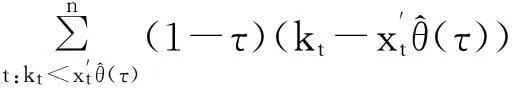
(7)
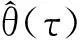
3.模型的诊断与检验
1)拟合优度检验。针对分位自回归模型拟合优度的检验,可以直接将分位数回归拟合优度的方法与传统时间序列中的拟合优度方法相结合。Koenker和Machado提出了分位数回归拟合优度的检验方法,给出了QAR模型拟合优度的表示形式[10]:
(8)

2)参数显著性检验。Koenker和Bassett基于Wald方法,研究了向量ζ=(θ(τ1)T,θ(τ2)T,…,θ(τq)T)T的广义线性检验,提出参数显著性检验的零假设为H0∶Rζ=r,同时选取了参数显著性检验的T统计量为[9]:
(9)
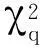
3)非对称性检验。Koenker和Bassett(1982)还提出了关于分位回归模型的非对称性检验方法,通过判断不同分位数τ所对应的回归参数(回归方程斜率)是否相等的方法,这种方法也可以直接用到QAR模型中。因此,针对本文所建立的QAR-Lee-Carter模型,进行非对称性检验时,零假设设定为:
H0∶θ(τ1)=θ(τ2)=…=θ(τq)
(10)
其中,θ指不包含常数项的解释变量所对应的(p-1)维参数列向量。Koenker、Xiao和Fan基于Wald统计量提出了QAR模型非对称性的检验方法,认为检验不同分数的回归系数是否相等,只需检验θj(τ)=μj,j=1,2,…,p是否成立[11]。
4)误差项的自相关检验。分位自回归模型误差项的自相关检验,可以根据传统的时间序列模型来构建。Box和Pierce(1970)构建了Q统计量,来检验残差序列是否为白噪声过程。本文直接将Q统计量引入到QAR模型的残差自相关检验中,Q统计量为:
(11)
4.预测
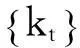
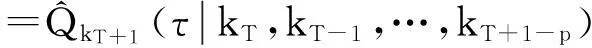
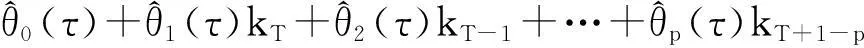
(12)
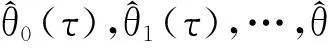
(13)

三、实证分析
(一)数据与假设
本文的数据选取于1995—2006年的《中国人口统计年鉴》,以及2007—2013年的《中国人口和就业统计年鉴》中的分年龄、分性别的全国人口死亡率,得到1994—2012年死亡率数据,共计19年。其中, 2000年与2010年的死亡率数据来自人口普查,1995年与2005年的数据来自1%的抽样调查,其他年份的数据来自于人口变动抽样。结合数据本身的特点以及实证分析的需要,本文对数据做如下处理和相应的假设:
选取男性人口的死亡率为代表进行研究。
将男性人口死亡率按5岁一个年龄段进行分组,即0~4岁,5~9岁,…,75~79岁。由于80岁以上人口数量较少,所得到的死亡率的可信度较低,因此本文将不对80岁及以上人口的死亡率进行研究。未来80岁以上人口死亡率的计算,可以根据80岁以下人口死亡率的分布规律,选取恰当的死亡率参数(或非参数)模型,通过外推法得到。
假定1%的人口抽样调查与变动抽样方法均具有较好的随机抽样特征。同时,根据不同年龄组的死亡率数据,以100万为基准对各年龄段的死亡人数进行调整。
(二)Lee-Carter模型的参数估计
1.αx与βx的估计
根据本文给出的Lee-Carter模型的参数估计步骤,可以分别计算得到各参数的估计结果。首先通过图1与图2来展示αx与βx的估计值。
从图1中可见,αx随着年龄组的增加,呈现出先降后增的趋势,很好体现了死亡率随年龄变化的趋势。同时可以看到,αx的最小值落入了10~14岁这一年龄组,表明人口死亡率随年龄变化的驻点在10~14岁之间,这些结果均符合中国人口死亡率的一般规律。图2给出了不同年龄组βx的估计值。总体上,βx随着年龄组呈现递减趋势,低年龄组的βx值较高,高年龄组βx值较低,说明了低年龄组的死亡率与时间t的交互效应较为明显,即死亡率改善在低年龄组产生的效果要强于高年龄组。通过对比WLS和OLS下的估计结果,发现在低年龄组WLS估计得到的βx值大于OLS的估计值,而在高年龄组WLS估计得到的βx值小于OLS的估计值。这一结果意味着,在WLS方法下,低年龄组的βx与kt的交互效应更加显著,即低年龄组的人口死亡率改善效果更强;高年龄组的βx与kt的交互效应变得更小,则高年龄组的人口死亡率改善效果更弱。
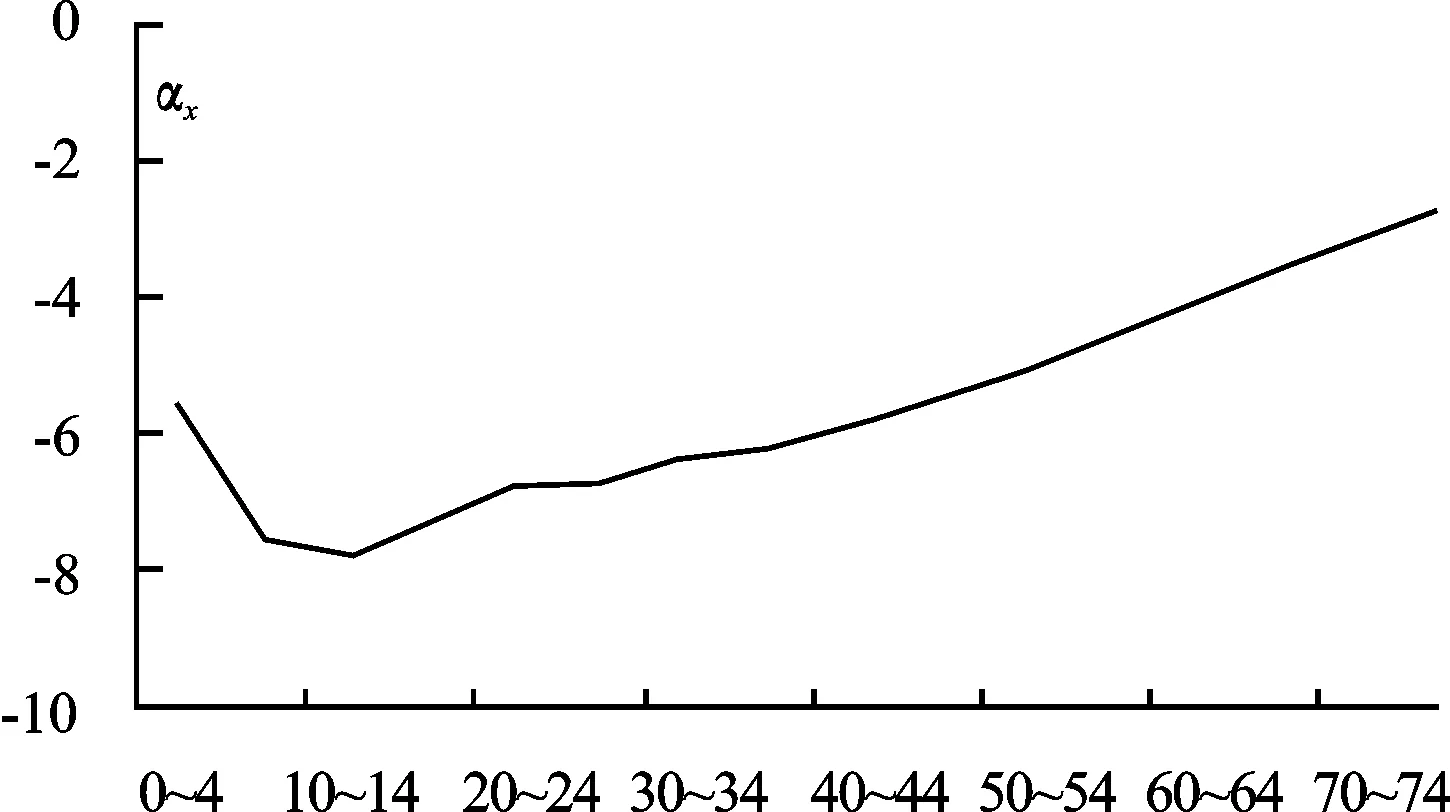
图1 不同年龄组α x估计值趋势图
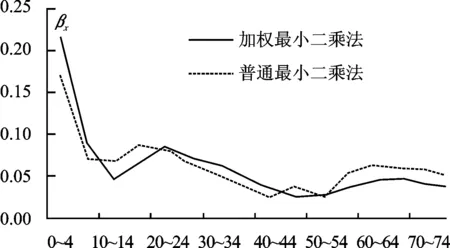
图2 不同年龄组β x估计值趋势图
2.kt的估计
kt估计值的变动趋势如图3所示。kt随时间t大体上呈线性递减趋势,但是在线性趋势下存在着一些波动,表明死亡率随时间推移而减小的速度较为稳定,与历史死亡率总体趋于下降的特征一致。其中,波动较为明显的点位于1998年与2008年,这两年的死亡率水平偏高主要与当年发生的自然灾害有关,如1998年的洪水、2008年的汶川地震,统计学中将这样的点称为离群点或异常值。针对时间序列kt,如果采用一般的ARIMA模型建模,为了保证模型的精度,需要将异常值去掉,这样将会损失大量样本信息,因此本文采取分位自回归对kt来建模,不需要去掉异常值,既可以保留尽可能多的样本信息,又可以对死亡率的波动性进行分析,较传统的时间序列建模方法具有明显的改善效果。
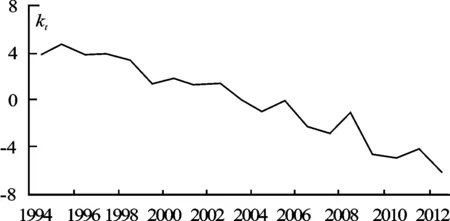
图3 不同年份k t估计值趋势图
(三)基于分位自回归模型的实证分析
1.模型的识别
针对时间序列kt建立分位自回归模型,首先要对原始序列kt(t=1994,1995,…,2012)进行平稳性检验。Dickey和Fuller(1979)提出了平稳性的单位根检验方法,随后很多学者采取不同的统计量建立了多种平稳性的检验方法,然而这些方法各有优缺点。为了保证检验结果的稳健性,本文采取平稳性检验最常用的三种方法,分别为ADF、PP(Phillips-Perron,1988)和ZA(Zivot-Andrews,1992)检验,检验结果如表1所示。
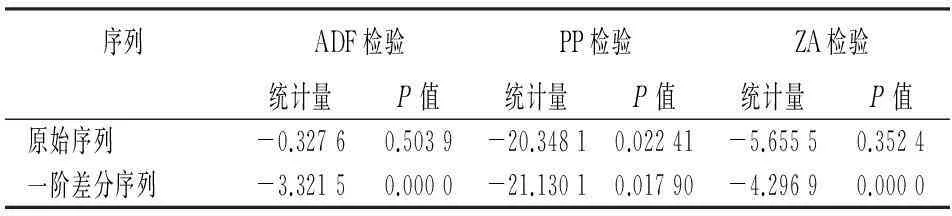
表1 k t序列平稳性检验结果
由表1可见,原始序列kt在三种平稳性检验方法下p值均较大,不具有平稳性。对原始序列kt的一阶差分序列再次平稳性检验的结果显示,在三种方法下检验得到的p值均较小,其中p值最大的为PP检验下的0.017 9,该结果也能保证一阶差分的平稳性在98%的水平下显著。因此,本文对kt的一阶差分序列建立分位自回归模型。
接下来确定分位自回归模型的最大滞后阶数。由于分位自回归模型具有多个分位点,要求针对每一个分位点都要确定最大滞后阶数,并且在不同的分位点其最大滞后阶数不同,这样便增加了分位自回归模型确定最大滞后阶数的难度。在实践中,通常采用一定的判定准则反复多次尝试后确定。本文选取7个重要分位点,同时采用AIC和BIC准则来判断针对kt的一阶差分序列所建立分位自回归模型的最大滞后阶数,结果见表2。表2给出了最大滞后阶数分别为1、2和3时不同分位点下的AIC与BIC值,相对于QAR(1)模型,QAR(2)模型在不同分位点处的AIC与BIC的值都有显著改善,如0.5分位点处,AIC的值从58.46降低到43.48,降幅为25.6%,BIC的值从60.13降低到45.80,降幅为23.8%,说明不同的分位点下,QAR(2)模型优于QAR(1)模型。下面比较QAR(3)与QAR(2)模型的优劣。在各个分位点下,AIC值和BIC值的降低幅度变小,如0.5分位点处,AIC的值从43.48降低到38.12,降低幅度为12.3%,BIC的值从45.80降低到40.95,降低幅度为10.6%。当滞后阶数为4时,AIC与BIC的值仅有微小的降低幅度,因此表2中未列示。尽管适当增加滞后阶数可增加分位自回归模型的拟合优度,但同时降低了自由度,因此将模型的最大滞后阶数限定在3。本文以AIC与BIC值的大小以及模型参数估计的显著性为依据,针对不同的分位点,在QAR(2)和QAR(3)之间选择最优模型。
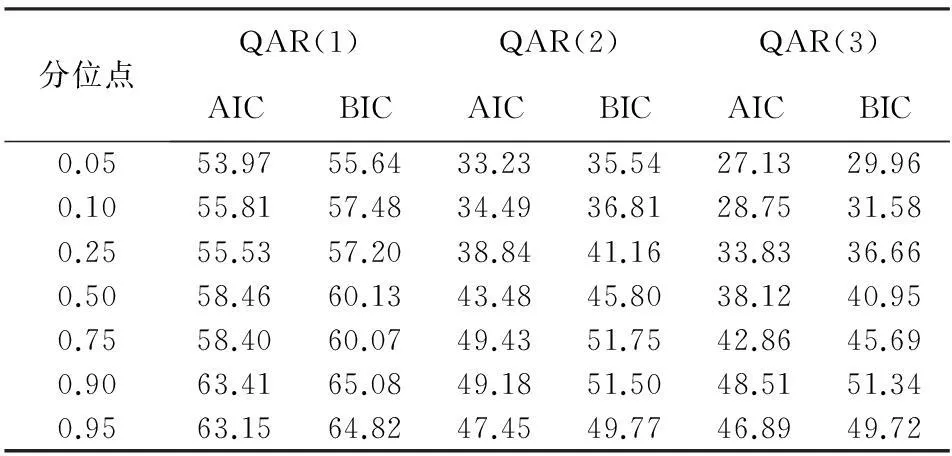
表2 不同分位点、不同滞后阶数的AIC与BIC值
2.参数估计与检验
分位自回归模型的特殊之处在于,不同的分位点可能存在不同的最优滞后阶数,因此还要配合参数的显著性检验来确定最合适的模型。接下来,在上一步模型识别的基础上,进行模型的参数估计与检验。分位自回归模型参数估计的前提是随机误差项ut是一个白噪声过程,同时假设误差项序列ut为i.i.d.的,因此本文基于上述假设,得到不同分位点处QAR模型的参数估计,结果见表3。
由表3可见,不同分位点处模型的参数估计值具有显著的差异,因此,所建立的分位自回归模型具有非对称性。针对模型的参数显著性检验分析三类模型的情况。QAR(1)只有在0.05、0.1和0.95分位点处所有参数的显著性检验能够通过,其他分位点处均不能通过。QAR(2)在0.05、0.10、0.25、0.5和0.95分位点处所有参数在1%的显著水平下均通过显著性检验,在0.75分位点处截距项与二阶滞后项不能通过显著性检验,0.90分位点处二阶滞后项不能通过显著性检验。QAR(3)仅在0.25分位点处在1%的显著水平下通过显著性检验,在0.05、0.1、0.5和0.75分位点处三阶滞后项均不能在10%的显著水平下通过显著检验,0.9分位点处模型可以通过10%显著水平下检验, 0.95分位点处模型可以通过5%显著水平下检验。为了得到1%显著水平下的最优模型,在0.05、0.1、0.5和0.95分位点处选择QAR(2)模型,在0.25分位点处选择QAR(3)模型,在0.75和0.90分位点处无通过检验的模型可选。因此,检验通过的分位点分别为0.05、0.1、0.25、0.5和0.95。根据所选择的分位自回归模型,通过计算0.05、0.1、0.25、0.5和0.95分位点处kt的预测值,发现0.95分位点处估计结果的残差不平稳,即0.95分位点模型的预测值不收敛,则该分位点处模型无效。通过对模型的参数和残差的检验,便可以舍掉0.75、0.9和0.95分位点,针对中国人口死亡率预测可选择的分位点仅限于0.05、0.1、0.25和0.5。经验数据表明,人口死亡率随时间变化呈下降趋势,低分位点的预测结果将获得较低的死亡率,高分位点将得到较高的死亡率。这样,本文所建立的分位自回归模型,舍掉了高分位点,保留了低分位点,很好地反映了未来死亡率降低的趋势,并且能够有效地应对人口死亡率被低估的现状。
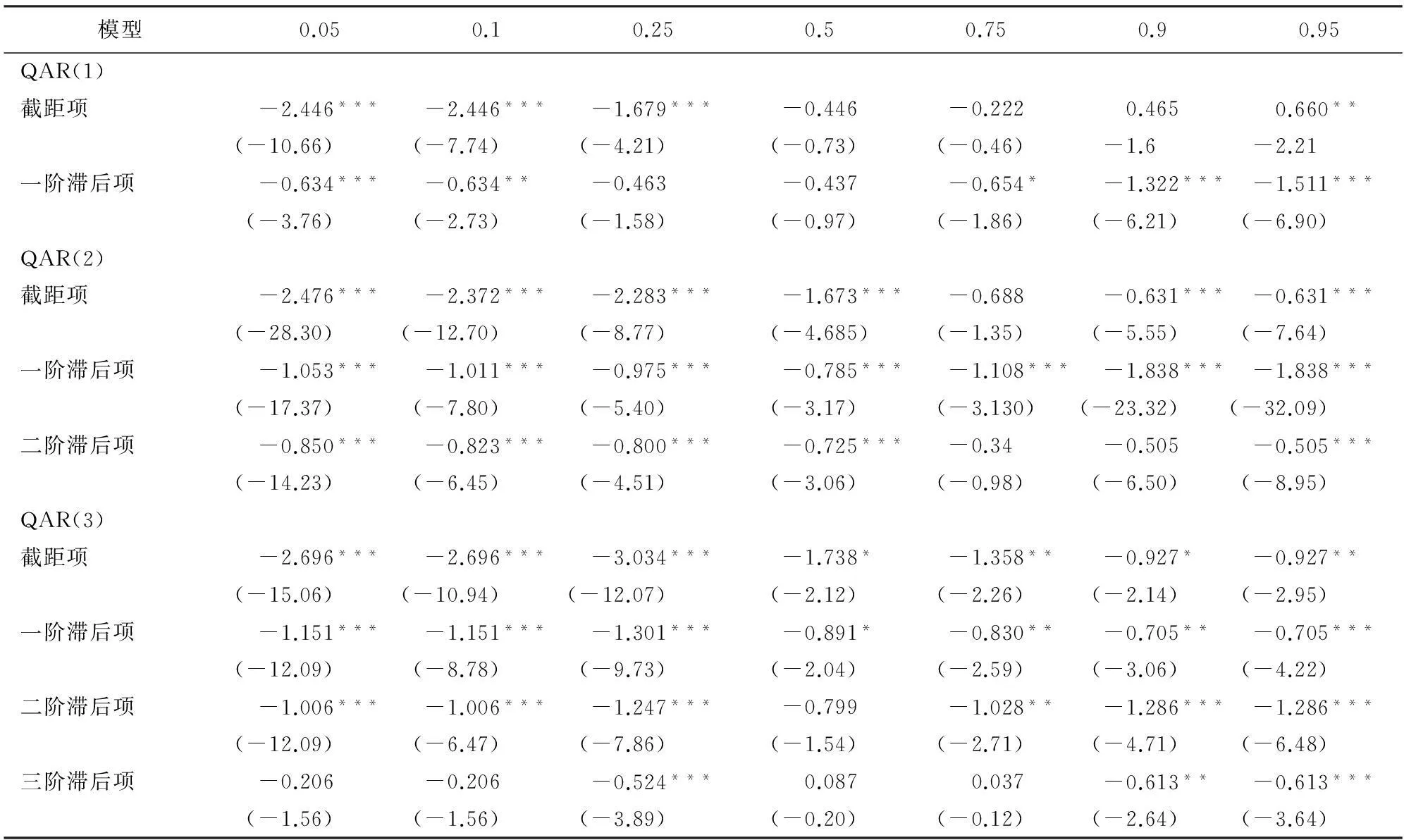
表3 分位自回归参数估计结果
注:括号内为t统计量值(假设残差是i.i.d.的,用Koenker和Bassett的方法计算得到近似的协方差矩阵)。***表示在1%水平下显著,** 表示在5%水平下显著,* 表示在10%水平下显著。
3.死亡率预测结果分析
针对不同分位点下死亡率的预测结果,本文选取三个有代表性的年龄组来进行分析,分别为0~4岁年龄组(婴幼儿组)、30~34岁年龄组(青壮年组)和70~74岁年龄组(老年组)。三个年龄组下不同分位点的死亡率未来趋势的分布特征由kt的趋势特征与αx和βx共同决定,预测结果见表4。由表4可见,每个年龄组均给出了0.5、0.25和0.1分位点的死亡率预测值,其中0.5分位点处的预测值作为死亡率的保守估计结果,0.25分位点处的预测值作为短期与中期预测结果的参照,0.1分位点处的预测值作为长期预测结果的参照。运用分位自回归预测方法可以得到更多的信息,通过对比分析不同分位点的预测结果,使得对未来死亡率改善的分析更加合理。具体来看,在0~4岁的婴幼儿组中,0.5分位点处的死亡率由2015年的0.074 6%,下降到2050年的0.000 5%,死亡率的改善幅度为99.3%,改善程度较高,且2050年0.1分位点处的死亡率为百万分之一,可见未来40年婴幼儿组死亡率改善得很充分。在30~34岁的青壮年组中,0.5分位点处的死亡率由2015年的0.099 6%,下降到2050年的0.023 1%,死亡率的改善幅度为76.8%,改善程度显著低于婴幼儿组。尽管青壮年组死亡率历史数据略低于婴幼儿组,但其死亡率改善程度较大幅度地低于婴幼儿组,因此2050年该组人口死亡率要显著高于婴幼儿组。在70~74岁的老年组中,0.5分位点处的死亡率由2015年的3.185 9%下降到2050年的1.253 5%,死亡率改善幅度为60.7%。老年组人口死亡率水平较高,其改善幅度较之前两个年龄组低。
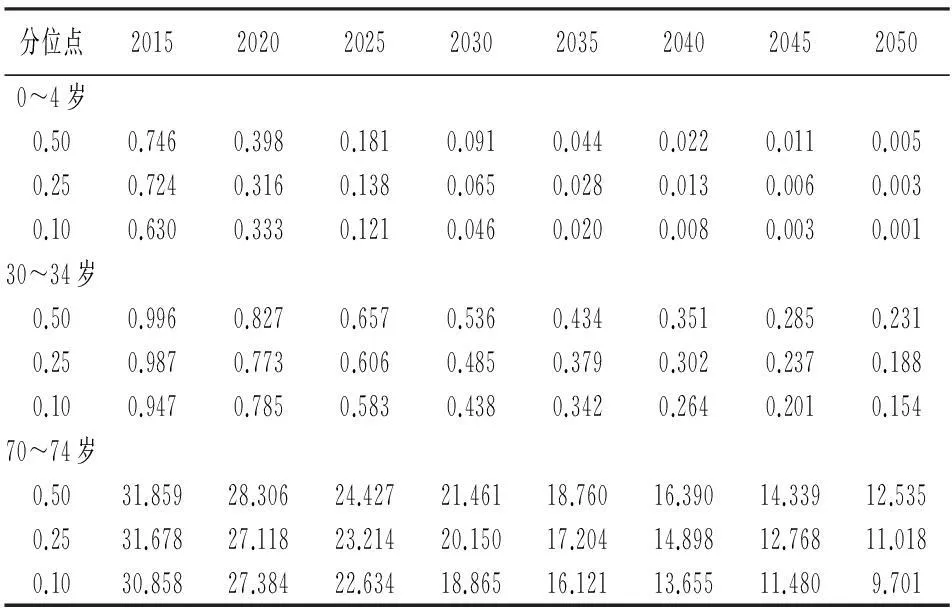
表4 不同年龄组死亡率的预测值 单位:‰
通过以上分析可知,中国未来40年人口死亡率的改善主要取决于婴幼儿组死亡率的改善,但随着时间的推移,婴幼儿组的人口死亡率将最先改善并达到极限水平,此时青壮年组和老年组人口仍有较大的改善空间。长期来看,中国未来人口预期寿命延长驱动力将逐渐由低年龄组向高年龄组过渡。
4.与相关研究的比较
本文旨在将分位自回归方法下的死亡率预测结果与相关研究进行比较,通过对比来验证本文研究结果的合理性。针对中国人口死亡率的预测,祝伟、陈秉正(2009)采用的是1989—2006年*其中1987—1988年、1991—1993年的数据缺失。中国城市人口死亡率数据,李志生、刘恒甲采用的是1992—2007年中国人口死亡率数据,王晓军、任文东采用的是6次人口普查的数据,而本文采用的是1994—2012年中国人口死亡率数据。尽管这些研究与本研究在数据选取上存在一定的差异,不能对预测结果进行直接比较,但本研究是在这些研究的基础上对kt因子提出的改进,只要对kt因子的拟合度进行比较,即可将本研究结果与其他学者的相关研究结果进行比较。由于以上学者的相关研究,均是采用均值回归方法(ARIMA模型)对kt进行的拟合,因此本文采用1994—2012年的中国人口死亡率数据*为了保证与相关研究结果具有可比性,本文使用相同的数据(同口径、同范围),按照相关学者的方法重新计算k t因子,并与本文的研究结果进行比较。,建立均值回归的ARIMA(0,1,0)模型对kt进行拟合,比较均值回归结果与本文分位自回归结果的优劣。
基于均值回归的ARIMA(0,1,0)模型表达式为:
kt+1=-0.541+kt+εt+1
(14)
其中,-0.541为常数项,是kt一阶差分后的均值;ε为误差项,ε~N(0,δ2),且有δ=1.325。
表5列示了不同年份kt的预测值与真实值偏差的绝对值。总均值表示从1998年到2012年的15年的偏差绝对值的均值。
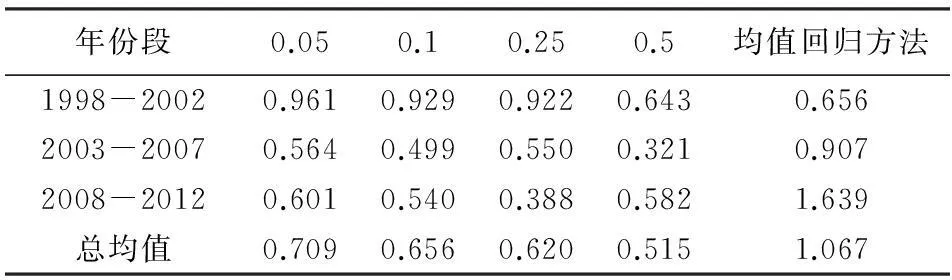
表5 不同年份 k t的预测值偏差平均值
从总均值角度看,分位回归方法在0.5分位点处的预测结果偏差最小,其次为0.25分位点处,预测偏差最大的为均值回归方法。具体来看,在1998—2002年,0.5分位点处的分位回归方法与均值回归方法得到的预测偏差最小,分别为0.643和0.656,且0.5分位点处的预测效果略优于均值回归的结果。在2003—2007年,0.5分位点处的预测偏差最小,其次为0.1分位点,预测偏差最大的为均值回归方法。2008—2012年,0.25分位点处的预测偏差最小,其次为0.1分位点,预测效果最差的为均值回归方法。可见,分位回归方法的预测效果总体上优于均值回归方法,且0.5分位点的预测效果最优,然而在最近的几年间,0.25分位点的预测效果最佳。通过以上分析可知,与均值回归方法相比,分位回归方法能够很好应对未来死亡率被低估的现状,且随着时间的推移,低分位点(如0.25分位点)的预测偏差将达到最小。针对中国未来人口死亡率的预测,没有绝对的最优分位点,本文选择0.5、0.25和0.1分位点进行预测,其中0.5分位点为整体角度的最优分位点,0.25分位点为近期预测的最优分位点,0.1分位点为长期预测的最优分位点。
四、结论与建议
本文将分位自回归方法内置到Lee-Carter模型框架中,构建中国人口死亡率分位自回归预测模型,对未来人口死亡率变动趋势进行预测,并将拟合结果与相关研究结果进行比较,得到结论如下:
其一,针对中国人口死亡率数据所构建的分位自回归模型,通过对参数显著性和预测结果残差平稳性的检验,舍掉了大于0.5的分位点,保留了0.5及以下分位点。本文所选的为常用分位点,并未对所有分位点进行检验。通过对0.6和0.7分位点处QAR(2)模型进行检验,得到0.6分位点处模型参数均在1%的显著水平下通过检验,且预测结果残差平稳,而0.7分位点则不能通过显著性检验。因此,针对中国人口死亡率分位自回归模型的分位点选取上,应根据不同研究需要,选择0.6及以下的分位点。
其二,通过对预测结果偏差的分析可知,任意分位点处分位回归方法的预测效果均优于均值回归方法,且0.5分位点处分位回归的总偏差最小,模型效果最优。然而,通过观测最近5年的平均预测偏差,0.25分位点处的预测效果达到最优,且0.1分位点处的预测偏差也低于0.5分位点处。可见,未来人口死亡率改善的趋势与程度均不会逆转,低分位点在预测人口死亡率方面将发挥出越来越明显的优势,为应对人口死亡率被低估的现状提供可选的方案。本文建议,选取0.5分位点处的预测值作为死亡率的保守估计,0.25分位点处的预测值作为短期与中期预测结果的参照,0.1分位点处的预测值作为长期预测结果的参照。
其三,运用分位自回归预测方法,可以得到更多的信息,对比分析不同分位点的预测结果,使得对未来死亡率改善的分析更加合理。通过对不同年龄组人口死亡率的预测可得,未来40年婴幼儿组死亡率改善程度较高,且很充分,进一步改善空间已不大;青壮年组死亡率历史数据略低于婴幼儿组,但其死亡率改善程度明显低于婴幼儿组,未来该组人口死亡率要显著高于婴幼儿组,死亡率仍存在进一步改善的空间;老年组人口死亡率水平较高,但是其改善幅度较之前两个年龄组低,存在较大的改善空间。从长期来看,中国未来人口预期寿命延长的驱动力将逐渐由婴幼儿组转向青壮年组和老年组。
参考文献:
[1]Antolin P.Longevity Risk and Private Pensions[R].OECD Working Papers on Insurance and Private Pensions,2007(3).
[2]Lee R D, Carter L R.Modeling and Forecasting U.S. Mortality [J].Journal of the American Statistical Association,1992(419).
[3]Wilmoth J R.Mortality Projections for Japan: A Comparison of Four Methods, Health and Mortality Among Elderly Population [M].New York: Oxford University Press,1996.
[4]Brouhns N,Denuit M,Vermunt J K.A Poisson Log-bilinear Regression Approach to the Construction of Projected Lifetables [J].Insurance: Mathematics and Economics, 2002(31).
[5]Siuhang Li,Waisum Chan.The Lee-Carter Model for Forecasting Mortality, Revisited [J].North American Actuarial Journa1,2007(121).
[6]李志生,刘恒甲.Lee-Carter死亡率模型的估计与应用——基于中国人口数据[J].中国人口科学,2010(3).
[7]韩猛,王晓军.Lee-Carter模型在中国城市人口死亡率预测中的应用与改进[J].保险研究,2010(10).
[8]王晓军,任文东.有限数据下Lee-Carter 模型在人口死亡率预测中的应用[J].统计研究,2012(6).
[9]Koenker R,Bassett G.Regression Quartiles [J].Econometrics,1978(1).
[10]Koenker R,Machado J A F.Goodness of Fit and Related Inference Processes for Quantile Regression[J].Journal of the American Statistical Association,1999(448).
[11]Koenker R,Xiao Z,Fan J.Quantile Autoregression [J].Journal of the American Statistical Association, 2006(475).
[12]陈建宝,丁军军.分位数回归技术综述[J].统计与信息论坛,2008(3).
Dynamic Forecasting the Mortality of China's Population on Quantile Autoregression
ZHAO Minga,WANG Xiao-juna,b
(a.School of Statistics; b.The Center for Applied Statistics, Renmin University of China, Beijing 100872, China)
Abstract:This paper improves the forecasting method of Lee-Carter model based on the data of the year 1994-2012 from the National Bureau of Statistics. We build a Chinese mortality model with quantile autoregression method to forecast the mortality trend in the future. Comparing the predicted results with the mean regression, we can get more information to overcome the mortality underestimate and make the future mortality prediction more reasonable and reliable.
Key words:quantile autoregression;population mortality; forecasting method
(责任编辑:杜一哲)

王雪标,男,辽宁锦州人,教授,博士生导师,研究方向:计量经济分析,金融风险管理。
【统计理论与方法】

