充填型断续裂隙扩展行为的分析研究

春军伟　曾仲毅

(贵州省交通规划勘察设计研究院股份有限公司　贵阳　550081)

充填型断续裂隙扩展行为的分析研究

春军伟曾仲毅

(贵州省交通规划勘察设计研究院股份有限公司贵阳550081)

摘要目前岩体断续裂隙扩展行为的研究主要集中在闭合型或张开型裂隙上，缺少对充填型裂隙扩展行为的研究。实践表明，实际工程中岩体裂隙内往往存在充填物，且充填物对裂隙扩展有一定程度的影响。文中在滑动裂隙模型的基础上，针对充填型裂隙的特点，考虑裂隙内的传压系数和传剪系数，并根据节理裂隙法向变形的双曲线模型，推导了充填型断续裂隙的法向刚度，最终结合最大拉应力准则提出了压剪作用下充填型断续裂隙张拉裂纹起裂参数的计算方法。

关键词充填物 断续裂隙扩展行为张拉裂纹起裂参数

岩体与一般介质的显著区别在于它是由结构面纵横切割而具有一定结构的多裂隙体，岩体中的结构面对岩体的变形和破坏起着控制作用。实践证明，岩体结构面是影响围岩稳定性的一个重要标志，围岩受到外部扰动后，在外荷载和自重作用下沿着结构面产生压缩、破裂和剪切滑移。其中，断续裂隙是岩体结构面的主要组成部分。由于裂隙的存在及其扩展控制着岩体的强度、变形和稳定性，准确地预测和分析岩体裂隙的力学行为是岩体工程实施的重要技术依据。

在实际工程中，岩体裂隙中往往会含有充填物，与不含充填物裂隙相比，充填物会使裂隙附近应力集中程度降低，并且充填物有一定的承压能力，而现有的少量试验结果也表明含充填物的裂隙扩展起裂荷载明显高于不含充填物的，且起裂位置向裂隙端部移动，起裂裂纹的多重发育也更加明显。目前，对岩体裂隙扩展的研究主要针对的是张开型裂隙和闭合型裂隙，对含充填物的裂隙扩展过程认识不够清晰。

无论是隧道开挖支护和边坡的治理，还是深部岩体的页岩气开采等工程，对岩体裂隙扩展过程的研究都是很有必要的，只有充分考虑到充填物对断续裂隙扩展的影响，才能为工程实践提供有力的理论依据和准确的指导作用。因此本文在压剪作用下的滑动裂隙模型[1-2]基础上，针对充填型断续裂隙的特点，考虑了裂隙的传压系数和传剪系数，并根据节理法向变形的双曲线模型[3]推导了充填型断续裂隙的法向刚度，根据最大周向拉应力断裂准则得到了充填型断续裂隙的张拉型裂纹(翼裂纹)起裂角和起裂应力的计算方法，为充填型断续裂隙扩展行为的研究提供了一定的基础理论研究。

1充填型岩体裂隙研究进展

对充填型岩体裂隙的分类主要是基于充填物与岩体的胶结情况，因此将岩体充填型裂隙分为胶结和非胶结2种[4]。胶结充填的强度通常不低于岩体的强度，因此，它不属于软弱面，胶结充填分硅质、铁质、钙质和岩脉充填等类型。非胶结充填裂隙内的充填物主要是泥质材料，其中含膨胀性的不良矿物(如蒙脱石裂隙、高岭石、绿泥石、绢云母、滑石等)较多时，其力学性质最差；含非润滑性质的矿物(如石英和方解石等)较多时，其力学性质较好。

目前，针对充填物对岩体裂隙力学性能影响的研究主要集中在充填物为黏土、碎石的情况，以模拟自然界中的天然节理裂隙的充填状态。例如，Papaliangas等[5]进行了一系列黏土充填节理的剪切试验，发现对于固定节理存在一个充填临界厚度，当充填厚度大于临界厚度时，最大剪切应力与压应力的比值趋于一个定值，而残余剪切应力所受影响不大；Pereira等[6]用沙子填充节理，指出剪切初期沙粒的滚动控制其强度，随着剪切中节理齿及充填物的磨损产生的微细粉末影响了沙粒的滚动，滑动占主导地位。但以上研究主要关心的是充填物对岩体的剪切强度的影响，很少对压剪作用下充填型断续裂隙的裂纹扩展行为进行研究。

赵永红[7]对含软弱断续夹层岩石材料进行了一定的研究，通过在大理岩上切缝灌入水泥砂浆，加载后观察试件中微裂纹的萌生、扩展等过程。张波等[8]通过在岩石相似材料中预制裂隙，并用树脂薄片代替充填物，做了一系列的单轴压缩试验，研究了裂隙充填与否对节理岩体峰值强度及峰后塑性变形能力的影响。Zhuang等[9]通过一定的装置将与真实岩体裂隙充填物相近的材料石膏预置在试件内，针对含有充填物和不含充填物的裂隙进行了较为详细的试验与数值模拟的对比研究。以上这些研究虽然考虑了充填物对断续裂隙扩展行为的影响，但只是在试验或数值层面进行了表观的研究，并没有对充填型断续裂隙扩展的力学机理进行深入的探讨。

2充填型断续裂隙扩展的力学模型

在岩石材料压缩断裂裂隙扩展机理研究方面，滑动裂隙扩展模型被众多学者采用[10-11]，见图1。考虑到充填物的影响，本文在原有的滑动裂隙模型基础上加入了传压系数和传剪系数，并根据节理法向变形的双曲线模型推导了断续充填型裂隙的法向刚度，根据最大周向拉应力断裂准则，求解得到充填型裂隙扩展的翼裂纹起裂角和起裂应力，见图2。

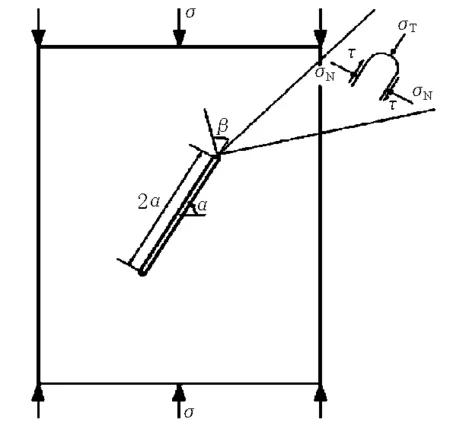
图1　滑动裂隙模型

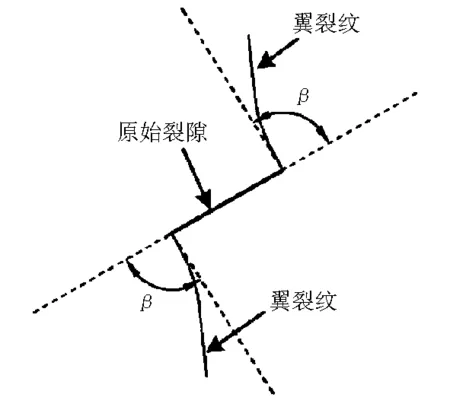
图2　翼裂纹起裂角

在滑动裂隙模型中，裂隙的远场应力表达

(1)式中：σN为原始裂隙远场法向压应力，垂直于裂隙面，MPa；σT为原始裂隙远场横向压应力，平行于裂隙面，MPa；τ为原始裂隙切向剪应力，MPa；σ为试样上作用的单轴荷载，MPa；α为裂隙的倾角，(°)。

对于有一定厚度t的裂隙在受压剪应力作用下，将只有部分应力沿裂隙面传递，徐靖南等[12]由此引入传压系数与传剪系数的概念，并给出如下结论。

(2)式中：E为试样的弹性模量，MPa；a为裂隙长度的一半，mm；υ为试样的泊松比；Kn为充填型裂隙的法向刚度，MPa/mm。

充填裂隙的法向刚度不仅与充填物材料、试样材料有关，还与裂隙的几何参数有关。因此本文尝试根据节理法向变形的双曲线模型给出含充填物裂隙的法向刚度的表达式，设裂隙被充填物完全充填，故暂不考虑节理面的粗糙度系数，而考虑充填物与试样材料的差别，故有

(3)式中：Kn为充填型裂隙的法向刚度，MPa/mm；Kno为充填型裂隙的初始法向刚度，由式(4)获得，MPa/mm；δmax为充填型裂隙厚度的最大压缩量，由式(5)获得，mm；σn为裂隙受到的法向应力，即σn=σN，MPa；A为常数，取0.8。

(4)式中：σc为完整试样的抗压强度，MPa；t为充填型裂隙的厚度，mm；E为完整试样的弹性模量，MPa；Ef为充填物的弹性模量，MPa；B，C为常数，取0.02和1×107。

(5)式中：D为常数，取0.1。

对于传剪系数，当|τ|≤|τm|=(1-Cn)σnfc+Cc时，此时裂隙面不产生相对位移Cs，裂隙面全部传递剪应力，则传剪系数为Cs=1。

当|τ|>|τm|=(1-Cn)σnfc+Cc时，此时裂隙内传递剪应力为τm，则此时裂隙面内的传剪系数为

(6)式中：fc为裂隙内的摩擦系数；Cc为裂隙内的粘聚力，MPa。

由于裂隙厚度和裂隙尖端曲率半径并非为0，所以与裂隙平行的横向压应力σT对裂隙扩展行为的影响不能忽略，横向压应力将在裂隙尖端附近产生拉伸应力，Muskhelishvihi[13]指出：横向压应力σT将在顶点附近产生与其相垂直的拉伸应力，其值近似和σT相等。因此对压缩状态下的裂隙其I型应力强度因子由2部分组成：法向压应力σN引起的KI(N)和横向压应力σT引起的KI(T)，即KI=KI(N)+KI(T)。

(7)

(8)式中：ρ为裂隙尖端的曲率半径，mm。

由上述结论可推导出含充填物裂隙尖端的I型应力强度因子KI的表达式：

(9)

假设新生裂纹未起裂前，充填裂隙内裂隙面与充填之间是没有相对滑移的，故此时的传剪系数Cs=1。

因此II型应力强度因子的表达式。

(10)裂隙尖端的应力场表达式为

(11)

上述表达式为线裂隙的解析解，对于钝型裂隙的尖端应力场表达式是有所不同的，而钝型裂隙的应力场表达式较为复杂，目前只有陈篪模型[14]对钝性裂隙的几何形态的表示较为准确，但应力场的表达式较为繁琐，故此处的推导还是按经典的裂隙尖端应力场来推导。根据最大周向拉应力断裂准则，当裂隙尖端周向拉应力达到临界值时，裂隙尖端翼裂纹将沿着最大周向应力的方向扩展(即与原始裂隙成β角度，起裂角的具体表示形式见图2)，此时满足裂隙尖端复合应力强度因子K达到最大值，并满足Kmax=KIc(KIc为试样材料的I型断裂韧度)。

即

(12)

为求得K的最大值，即满足下式：

(13)

求得

(14)

将式(9)和式(10)带入式(12)和式(14)中，令θ=β与σ=σw，即可求得翼裂纹的起裂角β和起裂应力σw。

3结语

本文总结了目前针对充填型断续裂隙扩展行为的研究，提供了基于滑动裂隙扩展模型的充填型断续裂隙扩展参数的计算方法，并充分考虑到了充填物对裂隙扩展力学行为的影响，为充填型断续裂隙扩展行为的研究提供了一定的理论依据。但本文也存在一定的不足之处，充填型断续裂隙扩展过程不仅存在张拉型裂纹，还同时存在反翼裂纹和次生裂纹，而反翼裂纹起裂是一个复杂的过程，起裂机理还不成熟，次生裂纹往往伴随着试样的破坏，起裂位置和起裂应力在物理试验中很难测得，且充填物与裂隙面随着压应力的增加，其间的接触问题将变得更加复杂，因此，无论从试验模拟，还是理论分析的角度，这些问题均值得进一步深入研究。

参考文献

[1]ASHBYMF,HALLAMSD.Thefailureofbrittlesolidscontainingsmallcracksundercompressivestressstates[J].ActaMetallurgica,1986,34(3):497-510.

[2]HORIIH,NEMAT-NASSERS.Brittlefailureincompression:Splitting,faultingandbrittle-ductiletransition[J].PhilosophicalTransactionsoftheRoyalSocietyofLondon,1986,319:337-374.

[3]BANDISSC,LUMSDENAC,BARTONNR.Fundamentalsofrockjointdeformation[J].InternationalJournalofRockMechanicsandMiningSciences&GeomechanicsAbstracts,1983,20(6):249-268.

[4]夏才初，孙宗颀.工程岩体节理力学[M].上海:同济大学出版社,2002.

[5]PAPALIANGAST,HENCHERSR,LUMSDENAC,etal.Theeffectoffrictionalfillthicknessontheshearstrengthofrockdiscontinuities[J].InternationalJournalofRockMechanicsandMiningSciences&GeomechanicsAbstracts,1993,30(2):81-91.

[6]PEREIRAJP.Rollingfrictionandshearbehaviourofrockdiscontinuitiesfilledwithsand[J].InternationalJournalofRockMechanicsandMiningSciences, 1997,34(3-4):241-244.

[7]赵永红.受单轴压缩大理岩填充割缝周围的微裂纹生长[J].岩石力学与工程学报，2004，23(15):2504-2509.

[8]张波，李术才，张敦福，等.含充填节理岩体相似材料试件单轴压缩试验及断裂损伤研究[J].岩土力学，2012，33(6):1647-1652.

[9]ZHAUANGXiaoying,CHUNJunwei,ZHUHehua,Acomparativestudyonunfilledandfilledcrackpropagationforrock-likebrittlematerial[J].TheoreticalandAppliedFractureMechanics,2014,72：110-120.

[10]李银平，杨春和.裂纹几何特征对压剪复合断裂的影响分析[J].岩石力学与工程学报，2006，25(3):462-466.

[11]杨庆，王超.基于扩展有限元的压剪复合断裂数值分析[J].岩土力学，2011，32(S2):568-572.

[12]徐靖南，朱维申，白世伟.压剪应力作用下多裂隙岩体的力学特性-本构模型[J].岩土力学，1993,14(4):1-15.

[13]MuskhelishviliNI.Somebasicproblemsofthemathematicaltheoryofelasticity[M].Leyden:Noordhoff, 1953.

[14]陈篪.论裂纹扩展的判据[J].金属学报，1977(S1):57-72.

收稿日期：2014-10-21

StudyontheFractureBehaviorofFilledCrack

Chun Junwei, Zeng Zhongyi

(GuizhouTransportationPlanningSurvey&DesignAcademeCo.,Ltd.Guiyang550081,China)

Abstract：Current research on the propagation behavior of rock cracks is mostly focused on open cracks and closed cracks, and it is rare to study on the filled cracks. While natural rock cracks are mostly found with filling materials and the fillings were also found to have strong influence on rock failure behavior in engineering practice. In this paper, the compression transferring coefficient and shearing transferring coefficient are taken into account in filled crack, which the normal stiffness is derivated based on the hyperbolic constitutive model of rock joint. Finally, the parameters of tensile crack initiation are computed by the crack sliding model and maximum tensile stress criterion.

Key words:fillings; rock crack; propagation behavior; tensile crack; initiation parameters

DOI10.3963/j.issn.1671-7570.2015.01.034