跨既有线大跨度曲线梁桥平转牵引力和摩阻系数测试分析研究

罗力军

(中铁大桥局集团武汉桥梁科学研究院有限公司　武汉　430034)

跨既有线大跨度曲线梁桥平转牵引力和摩阻系数测试分析研究

罗力军

(中铁大桥局集团武汉桥梁科学研究院有限公司武汉430034)

摘要在大跨度曲线梁桥平转施工中，发现按照常规计算公式计算的理论牵引力和摩阻系数与实测数据存在较大的偏差，为解决这一问题，有必要进行针对性的牵引力和摩阻系数测试分析研究。通过对不同结构支撑形式及转体形式建立相应的数学模型，进行公式推导和计算，并与实测数据进行比较分析，归纳总结出准确可靠且易于今后工程采纳的牵引力计算方法。同时对转体桥球铰安装施工提出合理化建议。

关键词既有线曲线梁桥平转牵引力摩阻系数分析研究

随着城市市政高架桥建设的大力投入，越来越多的涉铁项目得到开展。为了保证既有铁路线的正常运营和尽量少地干扰既有铁路线的运营，平转转体施工法得到越来越广泛的应用。在城市市政高架桥建设中，跨既有线平转施工桥梁上部结构一般为宽箱梁连续梁或者刚构桥，平转转动系统由支撑体系、转动牵引体系和平衡体系组成。支撑体系为上、下转盘和连接结构体；连接结构体主要有球铰、撑角等[1]。转动牵引体系为2组预埋在上转盘的钢绞线、反力座和大吨位连续千斤顶。平衡体系为桥面设置部分配重后和上部结构及球铰摩阻力一起达到自我平衡。

在转体过程中，如果牵引力计算不准确，则可能产生如下后果：

(1) 实际平转转体牵引力小于预估(或计算)最小值，转体能正常进行，但采用较笨重的设备进行转体施工造成施工效率和经济效益低下。

(2) 实际平转转体牵引力大于预估(或计算)最大值，转体不能正常进行，由于预估不足而在结构上施加过大的力，可能造成结构损坏或无法转体到位。

在平转牵引力计算时根据不同的支撑形式及转体形式等实际情况，认真分析其受力情况，采用数学方法进行分析，并与正式转体实测数据进行比较分析[2]。

1平转牵引力计算

平转牵引力计算方法采用力矩平衡的原则进行，即平转牵引力力矩与平转转动摩阻力矩大小相等。采用平面积分法进行公式推导：平面积分法计算时假定撑角与滑道、上下球铰均为全面积接触，忽略因滑片布置引起的接触空隙[3]。

全面积接触面都可以视为无数部分微圆环积分而成，见图1。部分圆环可以简化为一小矩形微元，微元面积rdθdr，微元所受压力力臂为r。

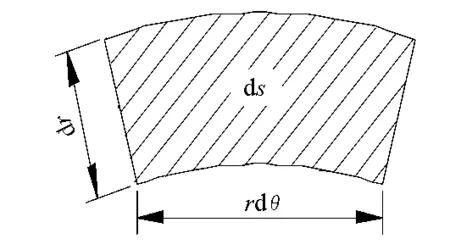
图1　平面积分面积微元

由积分推导出球铰处摩阻力矩M1为

(1)

撑角(单个)处摩阻力矩M2为

(2)

根据力矩平衡方程

M1+M2=Fl

最终牵引力F为

(3)

式中：p为支撑体系单位面积所受压力；μ1为球铰处摩阻系数；μ2为撑角与滑道摩阻系数；R0为球铰平面半径；R1为撑角内半径，R2为撑角外半径；l为牵引力力臂；F为牵引力。

球铰摩阻系数一般取静摩阻系数为0.10～0.12，动摩阻系数为0.06～0.09；撑角与滑道摩阻系数一般取静摩阻系数为0.05，动摩阻系数为0.03～0.04[4]。

2平转牵引力计算简化

一般转体桥施工球铰安装外包给有资质、有经验的专业单位安装施工，基本能保证球铰安装精度满足设计要求，转体前拆除球铰处的临时固结后，能保证撑角与滑道的间隙位于5～35mm[5]。笔者参与的2座曲线宽箱梁连续梁桥转体施工，转体前通过合理的配重和拆除球铰临时固结顺序，能保证撑角与滑道脱空，上部结构荷载完全由球铰承受，即支撑形式变为球铰独立支撑、小偏心转体。则式(3)简化为

(4)

式(4)与《公路桥涵施工规范》(JTGTF50-2011)中的转体牵引力计算公式一致。同时说明了“规范中”的牵引力计算公式仅适合于“转体结构自重由球铰独立承担，撑角不参与受力”的情况。

撑角与滑道存在接触，上部结构荷载不完全由球铰承受，即支撑形式变为球铰和撑角共同支撑、大偏心转体。计算平转牵引力时按照式(3)计算。

因此在转体桥牵引力设计时建议：正常转体牵引力设计值取式(4)计算值，不考虑撑角参与受力；备用助推设备顶推力考虑全部撑角受力，取式(3)计算值。

3平转牵引力实测值与理论计算值

鹦鹉洲长江大桥梅家山跨铁路主线桥上跨京广铁路，采用平面转体法施工。主线桥采用50m+85m+50m变高度预应力混凝土连续梁体系，桥面宽26.0～35.0m，梁高2.5～5.0m。转体总吨位10 000t，球铰球半径7.0m，平面半径1.75m。

现场测试的转体牵引力实测值见表1。

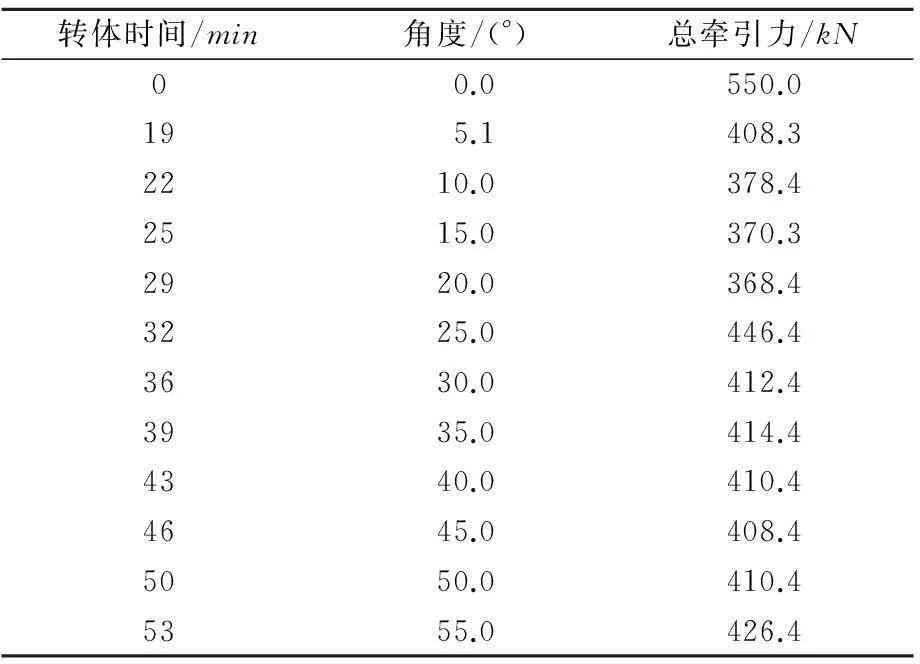
表1　正式转体实测数据

正式转体前进行了1.8°的试转，试转时初次启动力为1 080kN，正式转体时启动力为550kN。试转时，结构在初始启动时因放置时间较长，影响牵引力大小的因素很多，启动力会比较大。本桥转体初次启动力约为正式转体启动力的1倍，与其他文献数据2倍吻合[6]；正式转体时启动力550kN，理论计算值为1 341.0kN，实测牵引力计算所得最大静摩阻系数μ=0.041 1。正式转体中间过程牵引力大小稳定，转体过程平稳，牵引力平均值F=404.9kN，理论计算值为804.6kN，实测牵引力计算所得动摩阻系数u=0.030 2。

由计算值与实测数据对比可知，实测的牵引力小于计算值，换算摩阻系数小于设计一般取值。由于球铰安装精度较高，初始安装时撑角与滑道间隙2.5～3.5cm，拆除球铰临时固结(一般为砂桶)时按照对称平稳拆除，基本使上球铰自由下落，能保证撑角与滑道间隙1.5～2.5cm，荷载主要由球铰承受，撑角不参与受力，总体牵引力较小。同时可知，平面积分法计算的牵引力具有较大的安全储备，能保证梁体的正常转体，可以在实际牵引力设计时采用此方法。

4结论

(1) 宽箱梁曲线梁桥平转施工，在施工过程中通过合理控制，在初始安装球铰间隙设置为2.5～3.5cm，拆除球铰临时固结(一般为砂桶)时按照对称平稳拆除，基本使球铰自由下落，能保证成桥与滑道间隙1.5～2.5cm，荷载主要由球铰承受，能实现更安全、更容易的转体施工。

(2) 牵引力设置时，可以按照球铰独立受力设置牵引力大小，按照撑角全部参与受力设置备用助推装置顶推力，不需要设置过大的牵引装置和设备，可以得到较高的施工效率和经济效益。

(3) 实测静摩阻系数和动摩阻系数较设计值偏小，与其他文献资料吻合，设计摩阻系数可以在转体施工中适当偏小取值。

(4) 规范中的牵引力计算公式只适用于球铰独立受力时的情况，不能盲目照搬规范上的公式，需要根据实际情况考虑是否撑角参与受力而采用新的公式计算。

参考文献

[1]胡素敏.桥梁转体施工方法及发展应用[J].交通世界,2008(1):129-130.

[2]郭宁,封卫江.桥梁转体施工过程中顶推力的计算和应用[J].辽宁工程技术大学学报:自然科学版,2008(2):230-232.

[3]孙聪,高日.特殊支撑体系的转体桥施工牵引力计算方法分析[J].铁道建筑,2011(2):45-47.

[4]JTGTF50-2011公路桥涵施工技术规范[S].北京:人民交通出版社,2011.

[5]申国朝.郑州市解放路跨线桥主桥设计与施工[J].桥梁建设,2012(5):57-62.

[6]孙全胜,王立峰,孙永存,等.万吨级斜拉桥水平转体施工监测[J].武汉理工大学学报：交通科学与工程版,2007(3):400-403.

Testing,AnalysisandStudyofHaulingForcesandFrictionalResistance

CoefficientsforSwivelErectionofLongSpanCurved

BeamBridgesSpanningExistingRailwayLines

Luo Lijun

(BridgeScienceResearchInstituteLtd.,ChinaRailwayMajorBridgeEngineeringGroup,Wuhan430034,China)

Abstract：Intheconstructionofswivelerectionofthelongspancurvedbeambridges,ithasbeenfoundthatthetheoretichaulingforcesandfrictionalresistancecoefficientscalculatedaccordingtotheroutineformulaediffergreatlyfromthedatameasuredinthefields.Toresolvetheproblemofthedifference,itisnecessarytotest,analyzeandstudytheforcesandcoefficientsaccordingtothespecificcases.Bywayofestablishingthecorrespondingmathematicalmodelsforthedifferentstructuralsupportsanddifferentcasesoftheswivelerection,therelevantformulaearededucted,calculated,theresultsofthecalculationarecomparedtothemeasureddataandanalyzedandthecalculationmethodsfortheforcesandcoefficientsthatarecorrect,reliableandareeasilyappliedtothefutureconstructionaresummarized.

Keywords:existingrailwayline;curvedbeambridge;swivelerection;haulingforce;frictionresistancecoefficient;analysisandstudy

收稿日期：2014-11-10

ResearchonReconstructionSchemeofLushui
SecondBridgeofNationalHighwayG107inChibi

Yan Shaobo

(HubeiProvincialTransportPlanningandDesignInstitute,Wuhan430051,China)

Abstract：The main technical standards of engineering and construction project combined with the project of Lushui Second Bridge's demolition and reconstruction in Chibi are introduced in this paper and the construction method of cast-in-place cantilever is compared with that of full support, considering various factors of the full use of support construction period, cost and the construction scheme of the main bridge. The influence of prestressed steel arrangement on the box girder structure stress is analyzed through the finite element analysis software. The results show that full support method can not only shorten the construction period but also make full use of construction facilities. Under certain conditions, the full support method has its unique advantages.

Key words:full support method; cast-in-place cantilever construction; structure stress analysis

DOI10.3963/j.issn.1671-7570.2015.01.016