纵弯转换球面超声振动聚焦系统谐振特性研究
第一作者李华男,博士,教授,1961年生
纵弯转换球面超声振动聚焦系统谐振特性研究
李华1,任坤2,殷振1,赵江江2,谢鸥1,吕自强2
(1.苏州科技学院机械工程学院,江苏苏州215001; 2.河南工业大学机电工程学院,郑州450007)
摘要:对由纵向振动换能器与薄球壳组成的纵弯转换超声振动球面聚焦系统进行理论、实验研究,揭示系统的振动特性。研究表明,系统具有完全与不完全两种谐振模式。 在不完全谐振模式下系统具有整体谐振及局部共振两种状态,在两种状态下系统均可实现谐振。 基于研究结果,提出系统在不同谐振状态下的设计方法。对新型聚焦系统设计、应用具有重要实际意义。
关键词:超声;振动;聚焦;纵弯转换;球壳
收稿日期:2014-02-19修改稿收到日期:2014-04-10
中图分类号:TB532文献标志码:A
基金项目:国家自然科学基金资助项目(51206063,51476070)
Resonance features of a new ultrasonic vibration focusing system based on longitudinal-flexural vibration conversion
LIHua1,RENKun2,YINZhen1,ZHAOJiang-jiang2,XIEOu1,LÜZi-qiang2(1. College of Mechanical Engineering, Suzhou University of Science and Technology, Suzhou 215001, China;2. College of Mechanical and Electrical Engineering, Henan University of Technology, Zhengzhou 450007, China)
Abstract:Here, a new ultrasonic vibration focusing system composed of a longitudinal vibration transducer and a thin spherical shell was proposed based on the principle of longitudinal-flexural vibration conversion. The resonance property of the new system was analyzed by means of the plate-shell theory, FEM method and tests. It was shown that the new system has two resonance patterns named complete resonance and incomplete resonance; under the incomplete resonance pattern, the system has two states of whole resonance and local resonance. The system design method was proposed for different resonance states based on the study results, it was of importance for the design and application of the new focusing system.
Key words:ultrasonic; vibration; focusing; longitudinal-flexural vibration conversion; spherical shell
超声聚焦作为超声振动技术应用领域在工程、医学等均有应用[1-4]。实现超声聚焦的方法主要有透镜聚焦、反射聚焦及球面自聚焦三类。其中球面自聚焦方法因能实现大功率聚焦,应用更广。所用球面自振动聚焦系统为用压电材料制成特定的球壳形状,并沿厚度方向极化。在超声电源驱动下沿厚度产生纵向振动,球面辐射振动能量经介质后在焦区实现聚焦[5]。由于球壳材料限制,辐射面振动幅值不能过大,由单一球壳难以实现大功率聚焦。另外,由于球壳纵振动与空气声阻抗差距较大,纵振动在空气介质中存在辐射效率低的问题。

图1 纵弯转换球面弯曲 振动聚焦系统结构示意 Fig.1 The schematic of the longitudinal-flexural vibration conversion spherical focusing system
李华等[6]提出采用纵向振动换能器与球壳组成纵弯转换系统,见图1。其中1为压电陶瓷换能器,2为纵振动变幅杆,3为弯曲振动球壳。将纵向振动换能器的超声振动转换成球壳的弯曲振动,球壳将弯曲振动辐射出去并实现聚焦。在此系统中换能器与球壳可用声学特性好的金属材料制造,实现大功率超声振动,增大球面辐射声功率能力。由于弯曲振动波与气体介质声阻抗匹配较好,系统可有更高的辐射效率。从应用需要出发,纵振动变幅杆及球壳中心有孔,形成中心带孔的纵弯转换球壳聚焦系统。本文主要研究该系统谐振特性与设计方法。
1理论分析
由图1看出,该系统可分解为纵向振动换能器与弯曲振动球壳两部分,换能器前端与球壳连接。据超声振动系统等效四端网络理论[1],系统等效阻抗网络见图2。
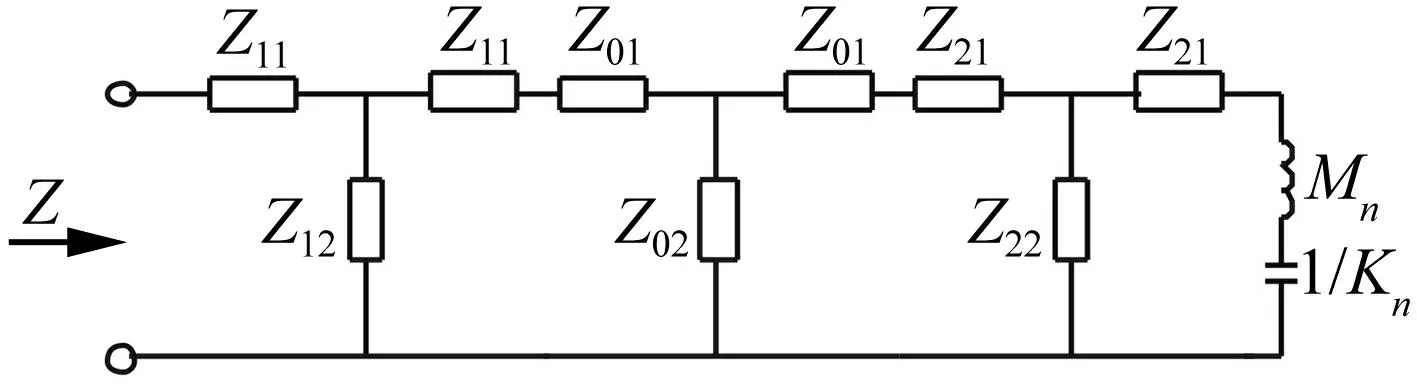
图2 纵弯振动转换组合系统的等效电路 Fig.2 The equivalent circuit of the longitudinal-flexural vibration conversion composite system

Xn=j(ωnMn-Kn/ωn)
(1)
当系统处于谐振状态时,其总等效阻抗Z为
(2)
式中:
1.1完全谐振状态下系统谐振与设计
振动系统中球壳厚度远小于口径及曲率半径,为方便分析可简化为无矩球壳。据无矩球壳弯曲振动理论[7],球壳弯曲振动振型方程为
w(φ)=C[APn(φ)+BQn(φ)]
(3)
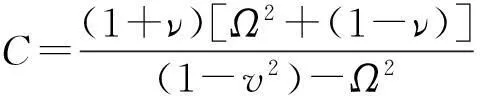
在满足工程应用需要基础上,得近似表达式[8]为
(4)
(5)
式中:J0,Y0分别为零阶第一、第二类贝塞尔函数。
考虑球壳外圆周自由及内孔与换能器端面连接的边界条件,设换能器前端振幅为W,可推得球壳弯曲振动速度方程为
(6)
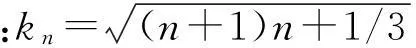
由边界条件

φ=φ0,(外圆周处)
得带孔球壳的弯曲振动频率方程为
n(n+1)[J2(knφi)Y1(knφ0)-Y2(knφi)J1(knφ0)]+
C(1+ν)[Y1(knφ0)J0(knφi)-J1(knφ0)Y0(knφi)]-
J1(knφ0)Y1(knφi)]=0
(7)
由式(7)可求出给定频率下球壳的结构参数。
球壳处于谐振状态时,式(1)中Xn=0。由式(2)知A1=0,即
(8)
式(8)即为纵振动换能器的谐振频率方程。在给定谐振频率情况下,由式(8)即可确定纵振换能器结构参数。该设计方法建立在系统中各部分均具有相同频率前提下,系统谐振频率与各组成部分谐振频率相等。由于组合系统结构复杂,本文提出的新型系统用数值方法设计,据应用要求确定球壳的口径、厚度、谐振频率等参数,用式(7)完成球壳曲率半径设计;再据谐振频率及球壳连接结构参数,用式(8)完成换能器设计。
1.2不完全谐振状态下系统谐振与设计
实际应用中很多情况下系统中球壳及换能器的谐振频率不相等,系统谐振频率与各组成部分的固有谐振频率亦不相等,虽换能器与球壳不处于谐振状态,但系统仍可处于谐振状态。此种状态即为不完全谐振状态。据谐振时系统各部分振动状态不同,不完全谐振状态可分为整体谐振与局部共振两种模式。
1.2.1整体谐振模式
由式(2)得
A1+jA2Xn=0
(9)

(10)
整个球壳的动能为
(11)

(12)
同理,以中心为参考点时圆盘的势能可表示为
(13)
据薄板弯曲势能密度定义,可推得圆盘弯曲振动时的总势能为
(14)

(15)
由式(1)、(2)、(12)、(15)即可求出不完全谐振状态下系统的整体谐振频率方程。据谐振频率方程,用数值解法可对整体谐振状态进行频率设计。在整体谐振模式下,组合系统呈现为具有复杂形状的振动系统特性,连接面位置对谐振频率不造成影响。系统的谐振频率与换能器及球壳的谐振频率不同。
1.2.2局部共振模式
由图1知,带孔的阶梯型换能器小直径段截面积及球壳厚度与换能器大直径段截面积差异较大。换能器前端与球壳内孔的连接面积及换能器两段直径连接处面积均较小。连接面两边结构呈弱耦合状态,此时力学连续性条件不完全成立,不能视为连续的整体系统。在耦合点两边,当小截面部分(称B系统)与大截面部分(称A系统)截面积相差较大时呈现不同特性。A系统呈现有负载系统的振动特性,耦合点耦合阻抗即为负载阻抗;B系统呈现一端固定振动系统在基础振动激励下的振动特性。在A、B系统固有频率不同情况下,当电源激励频率接近或等于系统B的谐振频率时A系统只产生微小振动,但该微小振动通过耦合连接处激励B系统,可使之处于谐振状态,产生大的振动输出。由于耦合连接处振幅较小,系统B近似于一端固定振动系统的谐振状态,即为 “局部共振”[9]表现。此时系统的谐振频率近似为 B系统在固定端边界条件下的谐振频率。本文所提聚焦系统在一组结构参数下的有限元分析结果见图3。
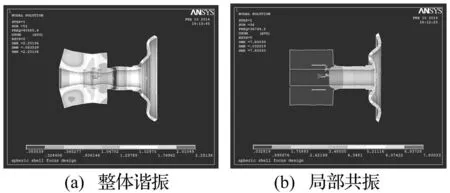
图3 聚焦系统两种振动状态 Fig.3 Two kinds of vibration state
由分析看出,不完全谐振是组合振动系统在各组成部分的谐振频率不相同时所特有的振动特性。系统工作在不完全谐振状态时各组成部分(如换能器、球壳)不一定工作在谐振状态,但系统整体工作在谐振状态。在系统输出端可得到理想的振动功率输出。据系统中各组成部分间结构耦合主参数大小不同及耦合连接处状态不同,不完全谐振可表现为系统的整体谐振模式或局部共振模式。纵振动及扭转振动系统结构的主参数为横截面面积或直径;弯曲振动系统主参数为极惯性矩方向的截面高度或厚度。当相邻两部分间结构耦合主参数相差不大时(比值大于1/3)系统呈现整体谐振模式;当结构耦合主参数相差较大时(比值小于1/3)系统呈现局部共振模式[9]。两种模式下系统谐振设计均可据式(1)、(2)、(12)、(15)采用数值方法完成。对局部共振模式,由于系统谐振频率与B系统近似,故可通过单独求解B系统频率方程得到系统的谐振频率。本文所提纵弯转换球面聚焦系统,仅据球壳频率方程即可求得系统的谐振频率。
2球壳结构参数对系统谐振影响规律
2.1完全谐振情况下谐振频率
由理论分析知,完全谐振理论上为系统的最佳工作状态。在完全谐振时球壳及换能器的谐振频率相同,只需据式(7)、(8)计算换能器、球壳结构即可。完全谐振状态下球壳曲率半径对频率影响的分析结果见图4。分析条件为:球壳材料为铝,口径98 mm,内孔直径20 mm。图4中F1F,F2F为一、二阶谐振频率的有限元分析结果;F1t,F2t为由式(7)理论计算的一、二阶谐振频率。在不同阶次下,随曲率半径增大系统的谐振频率变化规律亦不同,即曲率半径增大,一阶谐振频率减小,二阶谐振频率增大,但各阶谐振频率变化均逐步趋向于各自定值。此定值即为相同口径、厚度的平面圆盘各阶弯曲振动谐振频率。式(7)为建立在无矩球壳理论基础上,球壳厚度增加时计算结果将产生误差。厚度t=2 mm,t=5 mm两种情况下谐振频率随曲率半径变化有限元分析结果见图5。由图5看出,厚度变化对高阶谐振频率影响更大,对低阶谐振频率影响较小。

图4 球壳曲率半径对谐振频率影响 Fig.4 The influence of spherical shell radius to resonance frequency
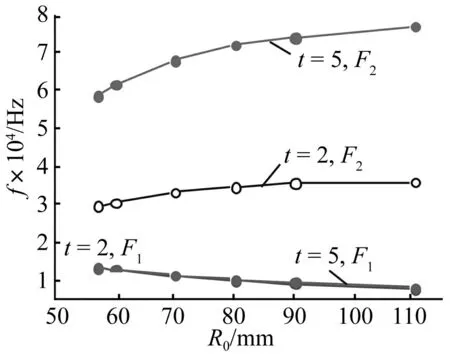
图5 球壳厚度对谐振频率的影响 Fig.5 The influence of spherical shell thickness to resonance frequency
与纵弯转换圆盘弯曲振动系统相比,本文的纵弯转换球面振动系统更具有一般意义。圆盘系统是球面系统的特殊情况。在其它结构参数相同情况下,球面曲率半径即为影响系统谐振频率的主要因素。因此在完全谐振状态下设计系统时,除按前述办法求数值解亦可利用圆盘弯曲振动方法设计,再据谐振频率修正,近似得到球面曲率半径。
2.2不完全谐振状态下谐振频率
设球壳材料为铝,厚度2 mm,口径98 mm。给定换能器结构参数,在60~160 mm范围内改变球壳曲率半径情况下,换能器与球壳的谐振频率不相等,系统大多处于不完全谐振状态。用FEM分析可得在不同球壳曲率半径下系统的谐振频率,见图6。其中图6(a)为不同曲率半径下前三阶谐振频率,图6(b)为在各阶谐振频率下有限元分析所得球壳与换能器大端相对振幅。图中FS,FK分别为系统及球壳的谐振频率;FH为换能器纵振动谐振频率;A为相对振幅;脚标1、2、3为谐振频率阶数。
由图6分析结果知,在不完全谐振状态下系统的谐振频率接近球壳的谐振频率。前2阶谐振频率远离换能器谐振频率,换能器大端仅有极微小振动,但球壳处于谐振状态,此时系统的谐振频率主要由球壳谐振频率决定,即系统的局部共振谐振状态;在第3阶谐振频率下系统谐振频率与换能器谐振频率相近,故此时系统谐振阻抗较前两阶小,系统输出功率大。由于换能器大端振幅增大,球壳相对振幅减小。“局部共振”状态时,由于换能器大端振幅小,故球壳的相对振幅明显大于整体谐振状态。球壳曲率半径较小时,两者差距更明显。随球壳曲率半径增大各阶频率下相对振幅趋近相同。

图6 不完全谐振状态下曲率半径对谐振特性的影响 Fig.6 The frequency characteristic of incomplete resonance
3实验研究
本文按新结构设计制做的纵弯转换球面弯曲振动聚焦系统见图7。其中球壳厚度2 mm, 曲率半径90 mm,口径75 mm、76 mm、77 mm三种。换能器大端直径50 mm,小端直径20 mm,长度为Lh,LX三种,见表1。

图7 纵弯转换球面聚焦系统实验结构 Fig.7 The experiment structure of the longitudinal-flexural vibration conversion spherical focusing system

换能器编号后盖板长度Lh/mm前端长度LX/mm118172203132233
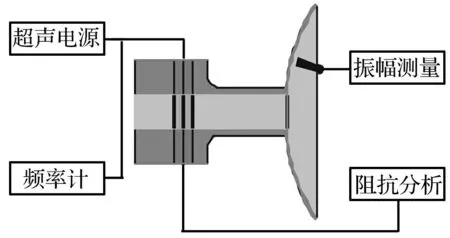
图8 纵弯转换球面聚焦 系统实验测试方案 Fig.8 The test scheme of longitudinal-flexural vibration conversion spherical focusing system
对三种结构换能器与三种口径的球壳组成的振动系统分别通过阻抗分析仪、光纤振动位移测量仪测试振动频率及振幅,获得各种结构的谐振频率、谐振阻抗及球面弯曲振动振幅分布曲线,实验系统见图8,实验数据及结构谐振频率的有限元分析结果见表2。其中因连接螺纹损坏,3号换能器与口径77 mm球壳组合系统未能完成测试。由表2看出,对不同的结构组合,系统虽处于不完全谐振状态,但均可较好实现纵弯转换谐振。在频率34 kHz附近谐振点,系统的谐振频率接近球壳谐振频率点,处于球壳局部共振状态;谐振频率为26 kHz时系统处于整体谐振状态。两种情况下系统均可较好实现谐振,但谐振阻抗有所不同。

表2 系统两种谐振状态实验数据

图9 球壳内表面振动位移实验结果 Fig.9 The test result of the spherical shell inner surface vibration
图9为2号换能器与口径75 mm球壳组成系统在两种谐振状态下球壳内表面沿经线方向等距点测得的弯曲振动振幅分布。其中序号1为球壳内孔边缘,序号17为球壳外缘。两种状态有限元分析结果见图10。由图9、图10看出,在两种振动状态下,系统均有较好的弯曲振动输出。实验中用阻抗分析仪测得2号换能器固有频率为31.44 kHz.。球壳固有频率约在34 kHz附近。由此知,在局部共振状态下,系统的谐振频率为球壳的固有频率。当换能器固有频率与该频率接近时,系统有较低谐振阻抗及较大振动输出,换能器与球壳连接处振幅较小,接近波节点,呈现局部共振特征;在系统整体谐振状态下,系统谐振频率与换能器及球壳固有频率不同,换能器及球壳连接处振幅较大,处于波节、波腹间近波腹位置。由于各连接部位耦合阻尼较大,系统谐振阻抗较大。有限元分析及实验表明,与局部共振相比,整体谐振时换能器大端振动明显增大。因实验所用电源与振动系统不匹配,在频率高的谐振点未实现大功率驱动,故振幅偏小。对1号换能器,实验测出整体谐振振型、谐振频率,但有限元分析却未发现整体谐振频率。其原因可能为换能器长度减小后整体谐振频率升高,与局部共振的谐振频率接近造成频率点重叠所致。
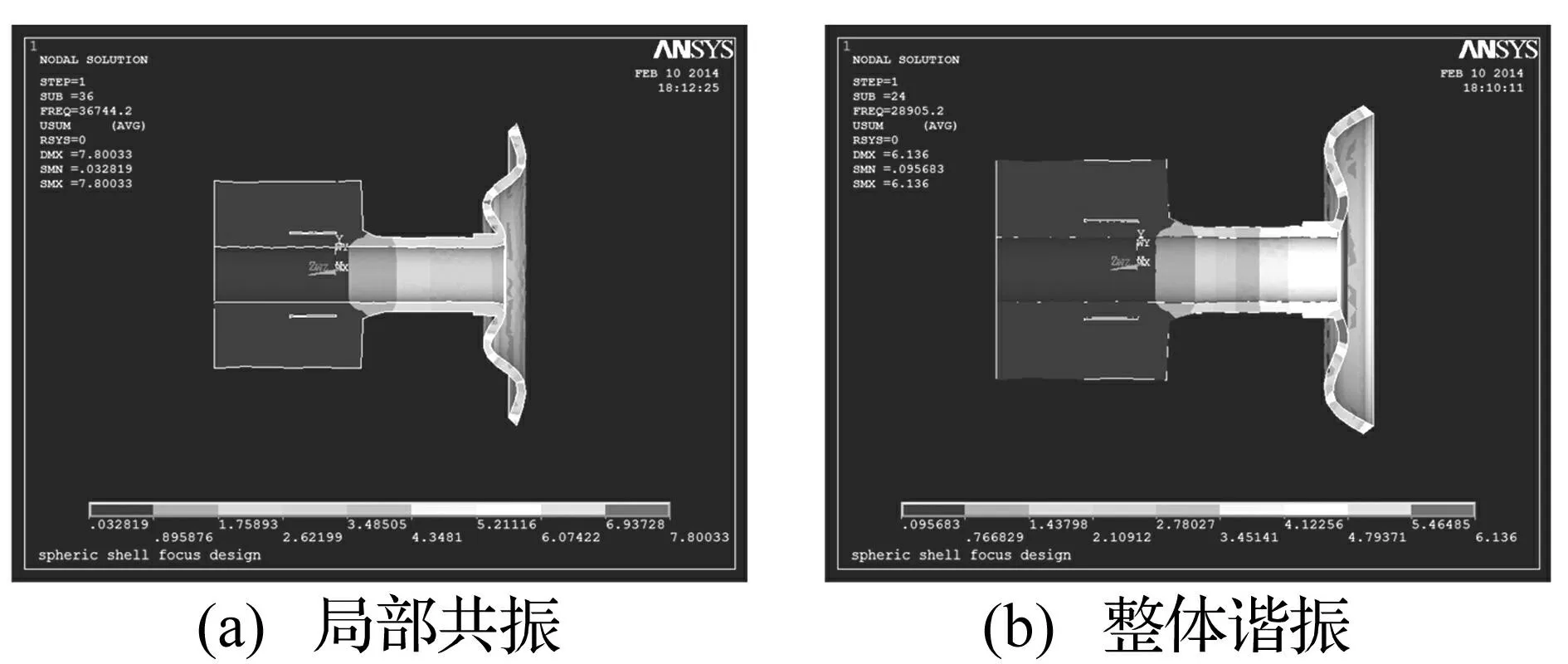
图10 球壳内表面振动FEM分析结果 Fig.10 The FEM result of the spherical shell inner surface vibration
综合分析知,完全、不完全谐振均为组合系统的谐振状态,为不同结构组合系统固有谐振特性反映。从理论上看,完全谐振状态为最理想状态;但实际结构中由于种种原因影响,此状态较不易实现。即使完全谐振状态系统工作时由于负载作用导致谐振频率偏移,系统亦处于不完全谐振状态。因此不完全谐振为组合振动系统更普遍的谐振状态。因两种状态均为系统谐振状态,故完全、不完全谐振均有理想的振动能量转换与输出效果[9]。本文研究的聚焦系统采用不完全谐振结构,经实验证明取得良好聚焦效果。组合系统的谐振阻抗主要受耦合连接结构的设计与制造质量影响,即使是完全谐振结构,耦合连接增加时系统的谐振阻抗也会明显增大。从设计角度看,完全谐振结构设计最成熟方便;不完全谐振结构设计则需用数值计算方法。在局部共振模式下系统设计也非常方便,且具有更强的使用灵活性、适用性及应用意义。
4结论
当球壳厚度较小时,可用无矩球壳理论分析球壳与纵向振动换能器组成的纵弯转换聚焦系统谐振。该聚焦系统存在完全、不完全谐振两种谐振模式。在不完全谐振模式下,本文提出的系统结构,存在整体谐振与局部共振两种状态。在整体谐振状态下谐振频率由换能器及球壳整体结构决定;在局部共振状态下谐振频率主要取决于球壳固有频率,不受换能器结构影响;因换能器振幅较小,球壳弯曲振幅较大,相当于仅球壳部分在谐振。 此现象对系统的设计及应用非常有用。
参考文献
[1]冯若.超声手册[M].南京:南京大学出版社,1999.
[2]Gangulia A, Gaob R X,Liangc K,et al. Optimal ultrasonic array focusing in attenuative media[J]. Ultrasonics, 2011,51(8):911-920.
[3]Pompeia A, umbatyanb M A,Trojan E A. An efficient calculation algorithm for focusing by plane ultrasonic transducers[J]. Applied Acoustics, 2006,67(5):420-431.
[4]Neild1 A, Hutchins D A,Robertson T J,et al. The radiated fields of focussing air-coupled ultrasonic phased arrays[J]. Ultrasonics, 2011, 51(8): 911-920.
[5]孙俊霞,寿文德.高强度聚焦超声换能器的新型设计[J].声学技术,2003,22 (2):80-82.
SUN Jun-xia, SHOU Wen-de. New design of high intensity focused ultrasound transducer[J]. Technical Acoustics, 2003,22(2):80-82.
[6]李华,任坤,殷振,等. 纵弯转换球面超声振动聚焦系统的声场与聚焦特性研究[J]. 压电与声光,2014(3):450-454.
LI Hua,REN Kun,YIN Zhen,et al. The sonic focusing properties of ultrasonic vibration spherical focusing system based on the longitudinal-bending vibration conversion[J]. Piezoelectrics & Acoustooptics,2014(3):450-454.
[7]曹志远.板壳振动理论[M].北京:中国铁道出版社,1989.
[8]宋启根.球壳振动问题的近似解[J].南工学报,1964(5):69-78.
SONG Qi-gen. The approximate sohltion of the symmetric vibration problems in spherical shells[J]. Journal of NanJing Institute of Technology,1964(5):69-78.
[9]应崇福,范国良. 超声复合振动系统中的“局部共振” 现象-20 年来的应用和机理分析情况[J].应用声学,2002,21(1): 20-25.
YING Chong-fu, FAN Guo-liang. The phenomenon of “local resonance” in compound ultrasonic vibration systems-applications and mechanism analyses during the 20 years after its discovery[J]. Applied Acoustics,2002,21(1):19-25.


