钢筋混凝土梁动态试验与数值模拟

第一作者李敏女，博士，讲师，1981年生

邮箱:cnlm225@126.com

钢筋混凝土梁动态试验与数值模拟

李敏1，李宏男2

(1.大连海洋大学海洋与土木工程学院，辽宁大连116023； 2.大连理工大学 建设工程学部，辽宁大连116024)

摘要：试验研究、数值模拟地震作用范围内加载速率对钢筋混凝土梁影响。试验研究混凝土强度、钢筋强度、剪跨比、加载速率及加载模式等对钢筋混凝土梁力学及变形性能影响；基于ABAQUS有限元软件建立钢筋混凝土梁计算模型，考虑钢筋、混凝土的率敏感性，对梁试件在不同工况下动态性能进行数值模拟；模拟结果与试验结果吻合较好。

关键词：加载速率；钢筋混凝土梁；地震作用；试验研究；数值模拟

收稿日期：2014-01-08修改稿收到日期：2014-03-12

中图分类号:TU375文献标志码：A

Dynamic tests and numerical simulation of reinforced concrete beams

LIMin1,LIHong-nan2(1. School of Marine and Civil Engineering, Dalian Ocean University, Dalian 116023, China； 2. Faculty of infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract:The effects of loading rate that might be experienced during earthquakes on reinforced concrete beams were experimentally and numerically studied here. Firstly, the effects of loading rate on mechanical properties and deformation of reinforced concrete beams were experimentally studied with the variation of several parameters including concrete strength, steel strength, shear span ratio, loading rate and loading mode. Then, based on the finite element software ABAQUS, considering the strain rate sensitivity of concrete and steel, the dynamic performances of reinforced concrete beams under different loading conditions were simulated, and the simulation results agreed well with the test ones.

Key words:loading rate; reinforced concrete beam; seismic loading; experimental study; numerical simulation

本文试验研究、数值模拟加载速率对钢筋混凝土梁的影响。考虑混凝土强度、钢筋强度、剪跨比及加载模式等参数，试验研究加载速率对钢筋混凝土梁力学及变形性能影响；并基于ABAQUS有限元软件建立钢筋混凝土梁计算模型，考虑钢筋、混凝土的率敏感性对梁试件在不同工况下的动态性能进行有限元数值模拟。

1试验内容

1.1试验概况

本试验所用钢筋混凝土梁共16根，长度均2 500 mm, 截面为矩形150 mm×250 mm，保护层厚30 mm。纵筋直径18 mm，配筋率1.6%；箍筋直径6.5 mm, 间距200 mm，配筋率0.22%。试件设计考虑混凝土强度等级(C30，C50)、纵筋强度等级(HRB335，HRB400)、剪跨比(λ=5.5，λ=3.0)、加载方式(单调及循环加载)、加载速率(0.05 mm/s，30 mm/s)。试验梁尺寸及配筋见图1。试件参数及不同工况下模拟与试验结果承载力见表1，其中试件编号含义为：B代表梁试件，30代表C30混凝土，50代表C50混凝土，S代表准静态加载，D代表快速加载，M代表单调加载，C代表循环加载，1代表剪跨比5.5，2代表剪跨比3。C30及C50混凝土试件(边长100 mm)立方体抗压强度实测值分别为36.94 MPa及49.22 MPa，HRB335及HRB400钢筋屈服强度实测值分别为381.62 MPa及428.25 MPa，箍筋屈服强度实测值为388.9 MPa。

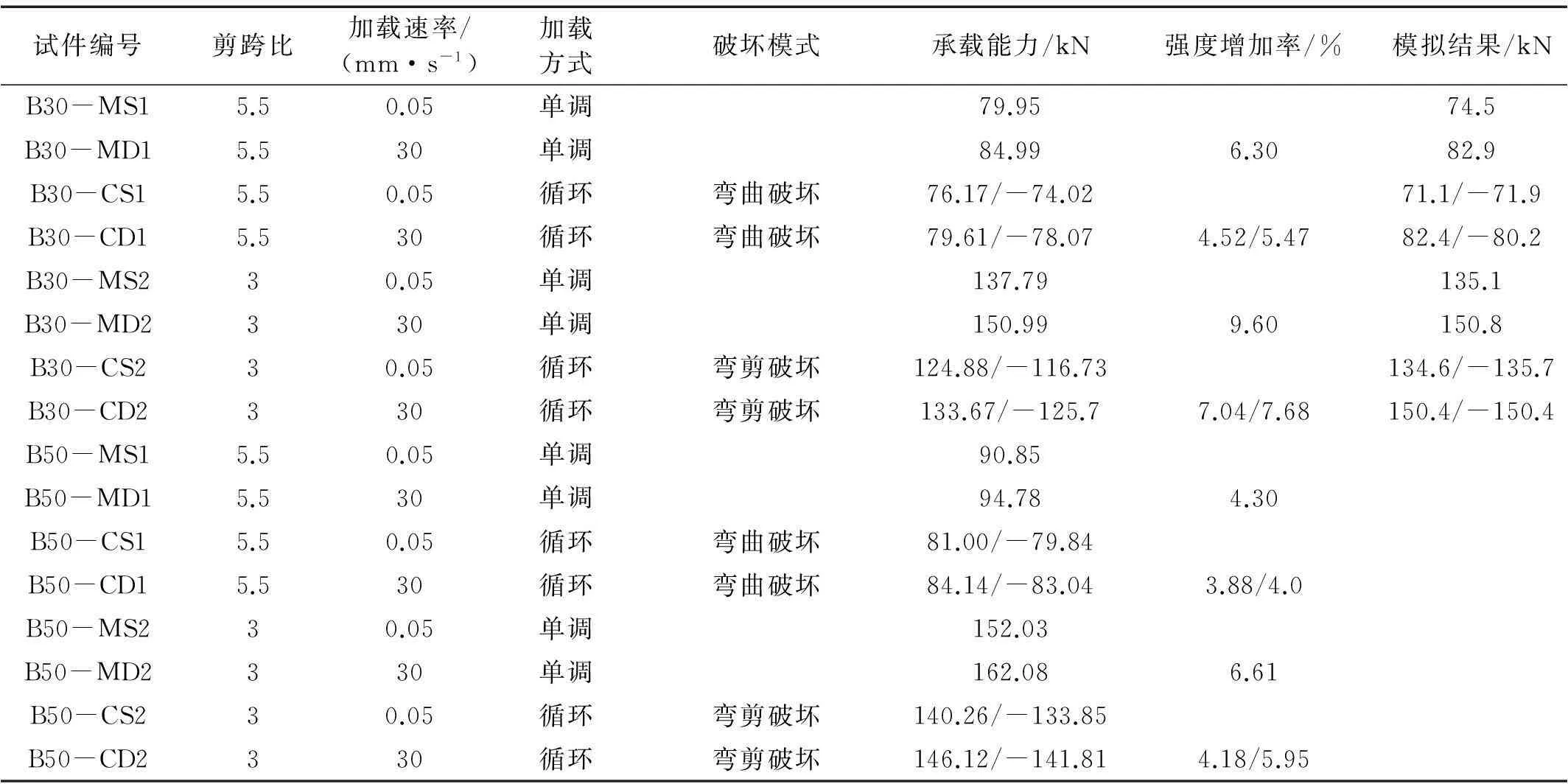
表1　试件参数及试验、模拟结果

注：表中承载能力为屈服段(上升段)最大承载力。

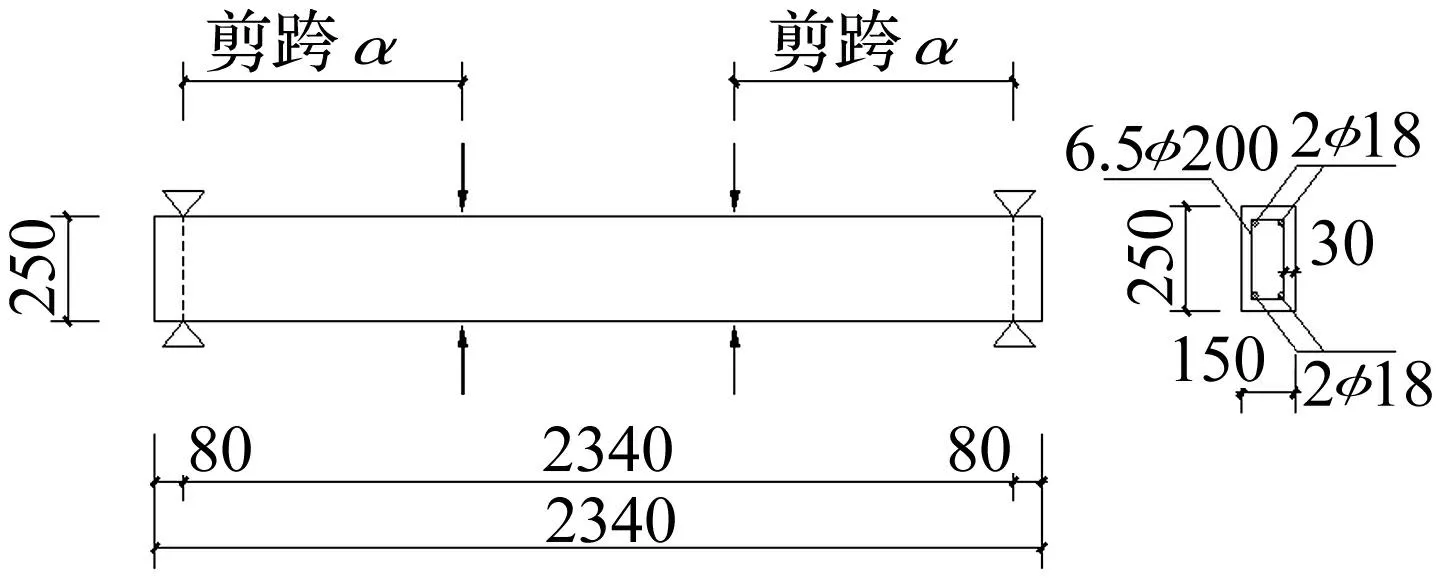
图1　试验梁尺寸、配筋示意图(单位：mm) Fig.1 Dimension and reinforcement of the beam

试验在大型静动三轴电液伺服试验机上进行，采用单调加载及三角波循环加载，见图2。循环加载幅值取屈服位移的整数倍(屈服位移定义为纵筋首次屈服时梁跨中位移)，每个幅值循环一次，采用位移控制模式加载，速率保持不变，慢速加载速率为0.05 mm/s,并与准静态加载对应；快速加载速率为30 mm/s，与地震作用时快速加载对应。

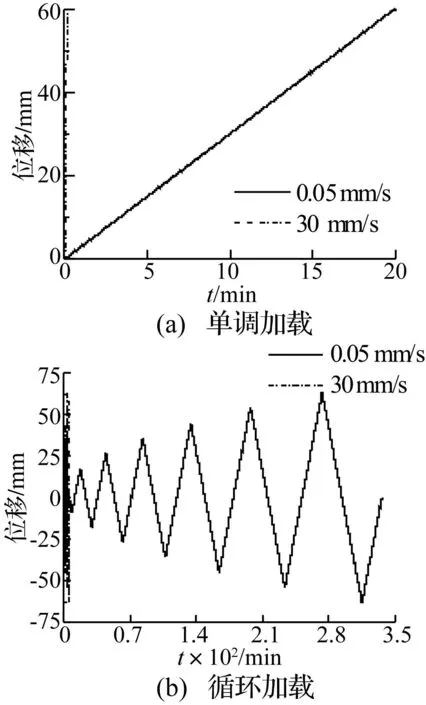
图2　两种加载方式 Fig.2 Two kinds of loading modes

1.2试验结果

据采集的数据，慢速加载时梁跨中受拉钢筋最大应变率量级为10-5/s, 快速加载时梁跨中受拉钢筋最大应变率量级为10-3/s, 剪跨段箍筋最大应变率量级为10-3/s。本文加载应变率量级在地震应变率范围(10-5/ s～10-1/s)，因此试验结果对研究地震作用下钢筋混凝土结构、构件响应有一定意义。

由试验所得各工况下钢筋混凝土梁跨中荷载-挠度曲线见图3。每种工况下梁的极限承载力见表1。由试验结果知：随加载速率提高各工况下梁的承载力均得到提高,组成梁的材料强度越高承载力提高越少。原因为混凝土、钢筋均为率敏感性材料，且应变率敏感性大小与强度成反比。对具有相同材料强度的梁，剪跨比越大，承载力提高越小。此因加载速率相对于加载点，剪跨比为5.5时加载点在跨中，而剪跨比为3时加载点与跨中距离为537 mm。因此对整根梁而言，剪跨比为3的梁实际加载速率较剪跨比为5.5的梁快，承载力提高的也多。

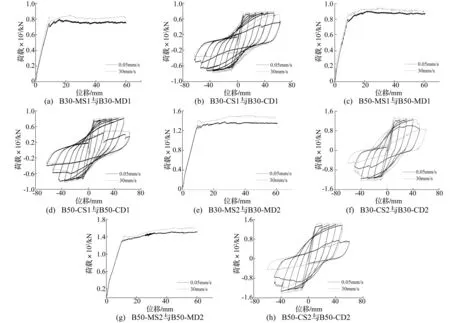
图3　不同加载速率下钢筋混凝土梁跨中荷载-挠度曲线 Fig.3 Load-displacement curves in the midspan of beams at different loading rates

对具有相同材料强度及剪跨比的梁，随加载速率提高循环加载较单调加载时强度增加少。此现象可能因在动态循环转折点位置钢筋、混凝土应变率几乎为零，而单调加载时钢筋、混凝土应变率大于零，因此循环加载对加载速率的敏感性较单调加载时小。

2数值模拟

2.1计算模型

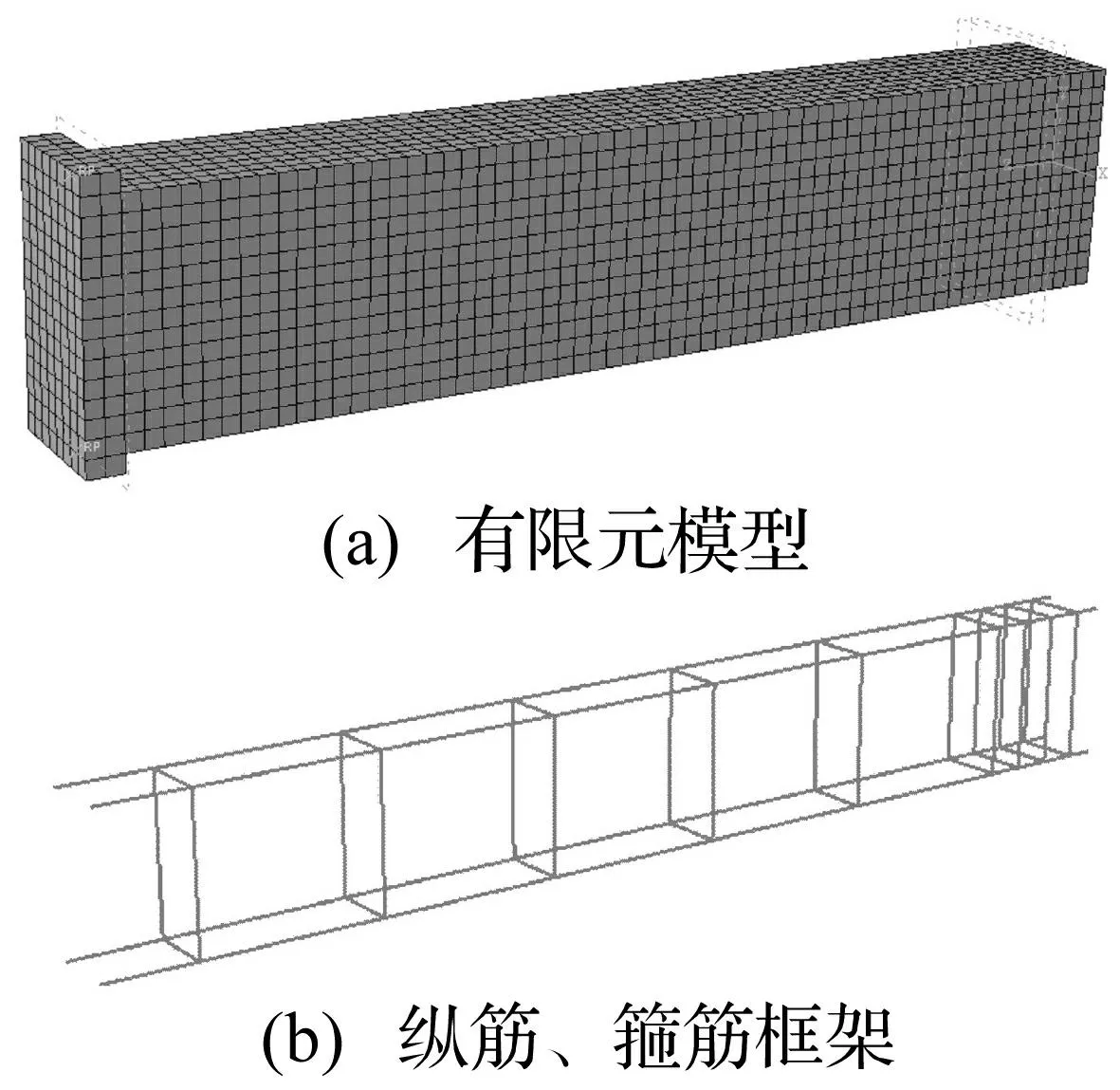
图4　钢筋混凝土梁有限元模型 Fig.4 Finite element model of reinforced concrete beam

用ABAQUS有限元软件对试验钢筋混凝土梁建模，由于梁试件具有对称性，为提高计算效率，取一半梁建模。混凝土采用8节点六面体减缩积分单元C3D8R，纵筋、箍筋采用2节点空间桁架单元T3D2，通过Embeded方式嵌入混凝土中，钢筋、混凝土间粘结滑移及裂缝间应力传递通过*tension stiffening命令近似模拟。混凝土单元尺寸20 mm×20 mm×20 mm,钢筋单元尺寸20 mm。用位移控制模式加载，为避免应力集中,在加载点放置刚性块，通过控制刚性块位移间接对梁试件加载。该梁有限元模型及纵筋、箍筋框架见图4。由于模拟主要关心加载速率对钢筋混凝土梁性能影响，故采用Dynamic,Explicit求解器显式求解。

2.2材料模型

2.2.1钢筋模型

钢筋模型应能模拟屈服面形状大小变化及Baushinger效应，且可考虑快速加载时钢筋的应变率效应；但由于试验所得最大钢筋应变基本处于屈服阶段或刚进入强化阶段，因此本文不考虑钢筋的强化，采用Mises模型模拟钢筋的本构关系，即用公式[11]模拟钢筋屈服强度的应变率效应。钢筋的动态与准静态屈服强度关系为

(1)

2.2.2混凝土模型

采用ABAQUS中混凝土损伤塑性模型模拟混凝土[12]。定义混凝土损伤塑性模型，需提供混凝土单轴拉、压率相关本构方程。

(1)混凝土单轴受压率相关本构方程

据已有研究成果，混凝土单轴名义受压应力-应变曲线形状与应变率无关。本文对不同应变率下混凝土单轴名义受压应力-应变曲线取相同表达形式。采用混凝土单轴受压本构关系[13]，其单轴受压率相关本构方程为

y=aax+(3-2aa)x2+(aa-2)x3， (x≤1 )

(2)

(3)

(4)

(5)

式中：aa、ad分别为上升、下降段参数；fcu为混凝土准静态立方体抗压强度(MPa)；DIF为混凝土单轴动态立方体与准静态立方体抗压强度比值，表达式[14]为

C30混凝土：

(6)

C50混凝土：

(7)

(2)混凝土单轴受拉率相关本构方程

(8)

式中：ftd，ft分别为当前应变率及准静态应变率下抗拉强度；εtfd为当前应变率下受拉峰值应变；E为弹性模量，本文设其与应变率无关。

动态与准静态抗拉强度关系采用Comité Euro-International du Béton (CEB)[15]模型，即

(9)

(10)

按弹性余能等效原理：在损伤状态下真实应力与应变对应的弹性余能及未损伤状态下有效应力与有效应变对应的弹性余能相等，得混凝土拉压损伤定义为

(11)

式中：Es为拉、压割线弹性模量；E0为拉、压初始弹性模量。

用本文试验所得边长100 mm混凝土立方体试块的抗压强度除以转换系数1.05，得混凝土立方体(边长150 mm)抗压强度fcu。混凝土棱柱体抗压强度fc计算式为

fc=0.8fcu

(12)

混凝土棱柱体抗拉强度ft计算式为

ft=0.26fcu2/3

(13)

混凝土模型所用材料参数见表2。其中fb0/fc0为双轴与单轴极限抗压应力之比；K为拉伸与压缩子午面第二应力不变量之比，本文取ABAQUS中默认值；aa，ad分别为混凝土单轴抗压应力应变曲线中上升及下降段参数，可由规范[13]获得。剪胀角为用于表示材料在剪切过程中体积变化率的物理量，据经验[9]及本文试验数据，本文取剪胀角为30。

2.3结果分析

计算获得钢筋混凝土梁最大自振频率为87.079 Hz,远大于本文加载的最大频率0.83 Hz，因此可忽略惯性作用对构件受力特性影响。对表1中前8种工况下梁试件进行数值模拟，所得跨中荷载-位移曲线见图5。由图5看出，加载速率越大梁的承载力越高；材料强度越低，应变率敏感性越大。不同加载工况下模拟与试验结果承载力差别不大。加载后期，模拟结果承载力下降偏快。滞回曲线形状与试验结果相差较大，模拟曲线较饱满，而试验曲线有捏拢现象。主要因计算模型未单独考虑钢筋与混凝土间粘结滑移及材料本构模型不够准确。总体而言，采用本文材料率相关本构模型、计算模型可模拟梁试件在不同加载速率下的主要特征。

表2　混凝土模型的参数

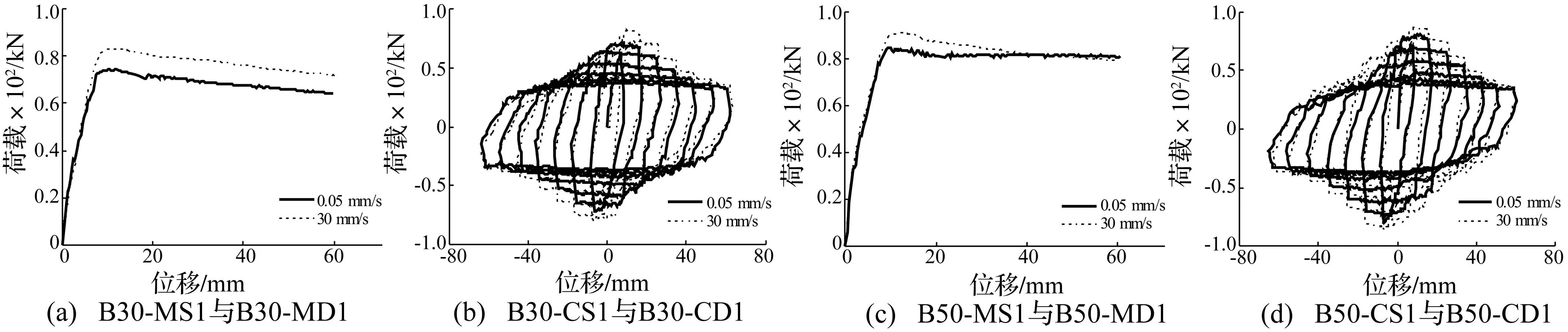
图5　钢筋混凝土梁数值模拟结果 Fig.5 Simulated results of reinforced concrete beams

3结论

本文对16根钢筋混凝土梁在不同加载速率下的受力、变形特性进行试验研究，考虑材料强度、剪跨比、加载方式及加载速率对钢筋混凝土梁特性影响，同时基于ABAQUS有限元软件对8种工况钢筋混凝土梁的动力特性进行数值模拟，结论如下：

(1)加载速率提高，钢筋混凝土梁的承载能力亦提高，其大小与梁材料强度、剪跨比及加载方式有关。强度越高承载能力提高的越少。相同材料强度的钢筋混凝土梁，剪跨比越大承载能力提高越小。梁的材料强度及剪跨比相同时，加载速率提高，循环加载较单调加载时强度提高的少。

(2)试验中材料应变率效应是快速加载下钢筋混凝土梁承载力提高的主要原因，惯性作用较小可忽略。

(3)基于ABAQUS有限元软件建立的计算模型可较好模拟钢筋混凝土梁的主要动力特性。

参考文献

[1]林峰,顾祥林,匡昕昕,等.高应变率下建筑钢筋的本构模型[J].建筑材料学报,2008,11(1):14-20.

LIN Feng, GU Xiang-lin, KUANG Xin-xin, et al.Constitutive models for reinforcing steel bars under high strain rates[J] Journal of Building Materials, 2008,11(1):14-20.

[2]梁磊，顾强康，原璐.AFRP约束混凝土多次冲击试验研究[J].振动与冲击,2013,32(5):90-95.

LIANG Lei, GU Qiang-kang, YUAN lu. Experimental research on AFRP confined concrete under repeated impact [J]. Journal of Vibration and Shock,2013,32(5):90-95.

[3]Bertero V V，Rea D, Mahin S, et al.Rate of loading effects on uncracked and repaired reinforced concrete members[C]. Proceeding of Fifth World Conference on Earthquake Engineering, Rome,1973(1):1461-1471.

[4]Kulkarni S M, Shah S P. Response of reinforced concrete beams at high strain rates[J].ACI Structural Journal, 1998, 95(6): 705-715.

[5]Fu H C, Erki M A, Seckin M. Review of effects of loading rate on reinforced concrete[J]. Journal of Structural Engineering, 1991,117(12):3660-3679.

[6]Pankaj P, Lin E. Material modeling in the seismic response analysis for the design of RC framed structures[J].Engineering Structures,2005,27:1014-1023.

[7]阎石,张亮,王丹.钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J].沈阳建筑大学学报,2005,21(3):177-180.

YAN Shi, ZHANG Liang, WANG Dan.Failure mode analysis for rc slab under explosive loads[J]. Journal of Shenyang Architectural and Civil Engineering Institute, 2005,21(3): 177-180.

[8]Wei J, Quintero R, Galati N, et al.Failure modeling of bridge components subjected to blast loading. part1:strain rate-dependent damage model for concrete[J]. International Journal of Concrete Structures and Materials, 2007,1(1):19-28.

[9]Chen L,Fang Q, Zhang Y, et al.Rate-sensitive numerical analysis of dynamic responses of arched blast doors subjected to blast loading[J].Transactions of TianJin University,2008,14:348-352.

[10]Shimazaki K, Wada A. Dynamic analysis of a reinforced concrete shear wall with strain rate effect[J].ACI Structural Journal,1998,95(5):488-497.

[11]李敏,李宏男.建筑钢筋动态试验及本构模型[J].土木工程学报, 2010,43(4):70-75.

LI Min, LI Hong-nan.Dynamic test and constitutive model for reinforcing steel[J].China Civil Engineering Journal, 2010, 43(4): 70-75.

[12]Lee J, Fenves G L. Plastic-damage model for cyclic loading of concrete structure[J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[13]GB50010-2002,混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2001.

[14]李敏,李宏男,张皓,等.中强混凝土应变率效应的试验研究与数值模拟[J].混凝土,2014(4):34-37.

LI Min, LI Hong-nan, ZHANG Hao,et al. Experimental and numerical study on the effects of strain rate of middle strength concrete[J].Concrete,2014(4):34-37.

[15]Eibl J. Concrete structures under impact and impulsive loading(CEB-bulletin d’information, NO.187) [R]. Dubrovnik: Comite Euro-International du Beton,1988.