基于结构损伤的在役钢框架地震易损性研究
第一作者徐强男,博士生,1986年生
通信作者郑山锁男,博士,教授,博士生导师,1961年生
基于结构损伤的在役钢框架地震易损性研究
徐强1,2, 郑山锁2, 程洋2, 韩言昭2, 田进2
(1.长安大学地质工程与测绘工程学院,西安710054; 2. 西安建筑科技大学土木工程学院,西安710055)
摘要:针对钢材锈蚀会致结构过早失效、需对不同龄期结构进行抗震性能评估问题,提出基于首超变形及累积塑性转角的双参数构件损伤模型;考虑构件与层权重系数建立结构整体损伤模型,定义结构4种破坏状态。通过已有钢材锈蚀规律引入时间参数,建立钢材多龄期本构与钢框架全寿命地震易损性模型,以9层梁柱焊接钢框架为例,选20条满足场地条件的地震波,对不同龄期(0年、25年、50年、75年、100年)钢框架分别进行动力增量(IDA)分析,所得不同龄期结构整体损伤指数与地震动参数(峰值加速度)之间满足指数关系,给出5个龄期、4种性能水平下结构易损性曲线。通过二次曲线回归拟合不同性态水平下结构破坏时峰值加速度(PGA)平均值及对数标准差与龄期关系,建立结构随龄期变化的连续失效概率函数,获得结构失效概率随龄期变化规律。
关键词:钢框架;结构损伤模型;易损性分析;全寿命;锈蚀
收稿日期:2013-10-21修改稿收到日期:2014-01-09
中图分类号:TU528.01文献标志码:A
Seismic vulnerability of steel framework in service based on structural damage
XUQiang1,2,ZHENGShan-suo2,CHENGYang2,HANYan-zhao2,TIANJin2(1.Geological Engineering and Surveying Engineering College,Chang’an University,Xi’an 710054,China;2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi’an 710055, China)
Abstract:The seismic performance of structures at different ages is necessary to be evaluated because the corrosion of steel may lead structure to earlier failure. A double parameters model for component damage based on the first super deformation and cumulative plastic corner was put forward to establish the overall structure damage model considering the weight coefficients for the component and layer, 4 kinds of damage states of the structure were defined. By introducing the parameter of time, the conventional rule for steel corrosion was used to establish the age constitutive and whole-life seismic vulnerability model of the steel frame. Taking a 9 floors frame with beam-column welded steel structure as an example. 20 seismic waves meeting the site conditions were selected to get the relationship between the overall damage index of structure and the peak ground acceleration (PGA) by using IDA analysis of steel frame at different ages (0 years, 25 years, 50 years, 75 and 100) in order to obtain the structure fragility curves of 5 instars and 4 performance levels. The relationships between the PGA mean value and age, as well as the PGA logarithmic standard deviation and age getting by quadratic curve regression analysis were used to obtain the continuous probability function of structural failure with the change of age.
Key words:steel frame; structural damage model; vulnerability analysis; life-cycle; corrosion
虽各国规范对钢材防腐均有明确规定,但钢结构因钢材锈蚀所致事故依旧频发,造成重大人员伤亡及经济损失。如2004年莫斯科一水上乐园因钢材锈蚀导致屋顶突然坍塌,伤亡人数达150人;2008年我国南方特大冰雪灾害中,一些刚投入使用的钢结构厂房倒塌原因为梁柱锈蚀导致结构承载力不足。通常情况下,结构的初始设计均能满足抗震需求,但材料因环境影响发生随时间的性能劣化使结构可靠度无法保证[1]。
结构易损性分析为评估结构性能的有效手段[2]。我国目前对钢结构锈蚀研究多集中于材性范畴,尚无对结构考虑锈蚀可靠度评估的研究。本文提出基于首超变形和累积塑性转角的双参数构件损伤模型,考虑构件与层权重系数建立结构整体损伤模型,基于已有近海环境下钢材随时间的锈蚀规律,建立钢材考虑锈蚀的多龄期本构与钢框架全寿命地震易损性模型,对不同龄期(0年、25年、50年、75年、100年)钢框架进行地震易损性评估,建立结构全寿命地震易损性模型,为灾后损失评估及震害预测提供理论依据与技术支持。
1结构损伤模型
1.1构件损伤模型
结构在地震作用下会产生不同程度损伤,并随荷载循环次数的增加不断累积,最终导致结构破坏。合理的损伤模型应物理意义明晰、应用简便,并能同时考虑结构位移首超破坏与累积损伤破坏。本文基于最大反应变形及累积耗能线性组合的双参数地震损伤模型[3],建立基于首超变形及累积塑性转角的双参数构件损伤模型,即
(1)

1.2损伤模型验证
为验证损伤模型的适用性,通过对钢框架节点损伤过程[5]进行分析,用有限元软件ANSYS建立钢框架节点有限元模型,利用已建损伤模型,对比由试验及有限元模拟计算的损伤值,见图1。模型初始条件、约束及加载制度与试验一致,并考虑初始缺陷。

图1 损伤模型验证 Fig.1 Validation of the damage model
1.3层损伤模型
据构件对整体结构损伤贡献确定构件的权重系数,由此获得整体结构损伤指数。本文定义结构层损伤模型为
(2)
式中:DI为结构第i层损伤指数;NS为第i层构件数量;ηj为构件j的权重系数,由构件滞回耗能对层滞回耗能所占比例确定,即
(3)
式中:Ej为构件j的滞回耗能;EI为第i层总滞回耗能。
1.4结构整体损伤模型
为能准确表达各层损伤对整体结构损伤贡献,需合理考虑层位置及层损伤对结构各层地震反应影响,而已有研究成果一般仅考虑单个因素。
(1)层位置权重系数
文献[6]的线性变化位置权重系数适用于刚度及屈服强度分布较均匀的框架结构,第i层位置权重系数表达式为
(4)
式中:N为结构总层数。
(2)层损伤权重系数
结构层损伤权重系数能直观反映本层结构损伤对整体损伤的贡献,表达式为
(5)
式中:Di为结构第i层损伤指数。
(3)层损伤权重系数
本文采用层位置权重系数与结构单层损伤权重系数共同确定层损伤权重系数,表达式为
(6)
式中:γi为第i层位置权重系数;μi为第i层损伤权重系数。
1.5结构整体损伤模型
本文基于构件与层权重系数的整体钢框架结构损伤模型为
(7)
式中:λi为第i层损伤权重系数;Di为第i层损伤指数;N为结构总层数。
1.6结构损伤状态
本文据所建结构整体损伤模型将结构损伤程度划分为无损、轻度损伤、中度损伤、重度损伤及倒塌5个等级,结构宏观性能描述见表1。定义结构不同损伤状态损伤指数范围及易损性分析时所用损伤指数极限状态值,见表2。

表1 钢结构损伤程度及宏观描述
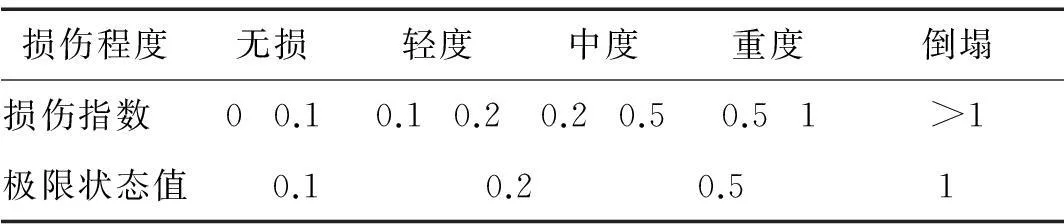
表2 结构损伤程度与损伤指数范围
2考虑锈蚀钢材多龄期本构
锈蚀导致钢材截面削弱、屈服点与峰值应力降低、应变减小,从而使结构承载力、可靠度降低,侧移增大,发生脆性破坏的可能增大。
2.1钢材本构考虑锈蚀影响的性能劣化
史炜洲等[7]采用室内盐雾加速锈蚀试验模拟近海大气锈蚀环境,通过对28个不同厚度不同锈蚀程度Q235B钢材材性试件的回归分析,获得钢材失重率与各性能指标之关系为
(8)

Dw=(W0-W1)/W0
(9)
式中:W0,W1分别为试件锈蚀前后质量。
2.2考虑锈蚀多龄期本构
钢材的锈蚀速率K一般取常数,用年锈蚀深度表示,则式(9)可改写为
Dw=l0Kt/A0
(10)
式中:l0,A0分别为锈蚀前构件截面周长、面积,均为常数;t为锈蚀时间,单位为年。
钢材锈蚀后,屈服点及屈服平台不明显,钢材弹性模量取锈蚀钢筋弹性模量值[8],即
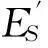
(11)
式中:ES,ES′分别为钢材锈蚀前后弹性模量。
建立锈蚀钢材随时间的本构关系为
(12)
3在役钢框架结构易损性分析
3.1在役钢框架易损性模型
结构需求参数D与地震动参数IM之关系满足指数关系[9],即
D=α(IM)β
(13)
结构易损性分析主要用于评估结构的抗震性能,计算不同强度地震作用下结构反应超过极限状态定义的结构能力参数条件概率。设结构地震需求D与地震能力C均服从对数正态分布[10],结构特定阶段失效概率Pf可表示为
(14)

引入时间参数考虑多龄期对结构地震需求参数影响,将式(13)改写为
D=α(t)(PGA)β(t)
(15)
将式(15)代入式(14),考虑多龄期结构特定阶段失效概率,表示为
(16)
上式可改写为
(17)
式中:m(t)为地震动参数PGA在结构不同破坏状态对应的平均值;n(t)为地震动参数PGA在结构不同破坏状态对应的对数标准差。
3.2计算模型
本文建立6榀3跨的9层梁柱焊接钢框架作为计算模型,单位mm,见图2。跨度均取6 m,层高均为3.6 m,梁为H型截面,柱为方型截面,梁柱截面尺寸见表3,钢材屈服强度同Q235。设计地震分组为第1组,场地类别为Ⅱ类,抗震设防烈度8度,设计基本地震加速度0.20 g。用ANSYS建立有限元模型,用应变硬化为3%的弹塑性模型模拟构件滞回性能,非线性动力分析时结构阻尼系数取3%,振型考虑前两阶。
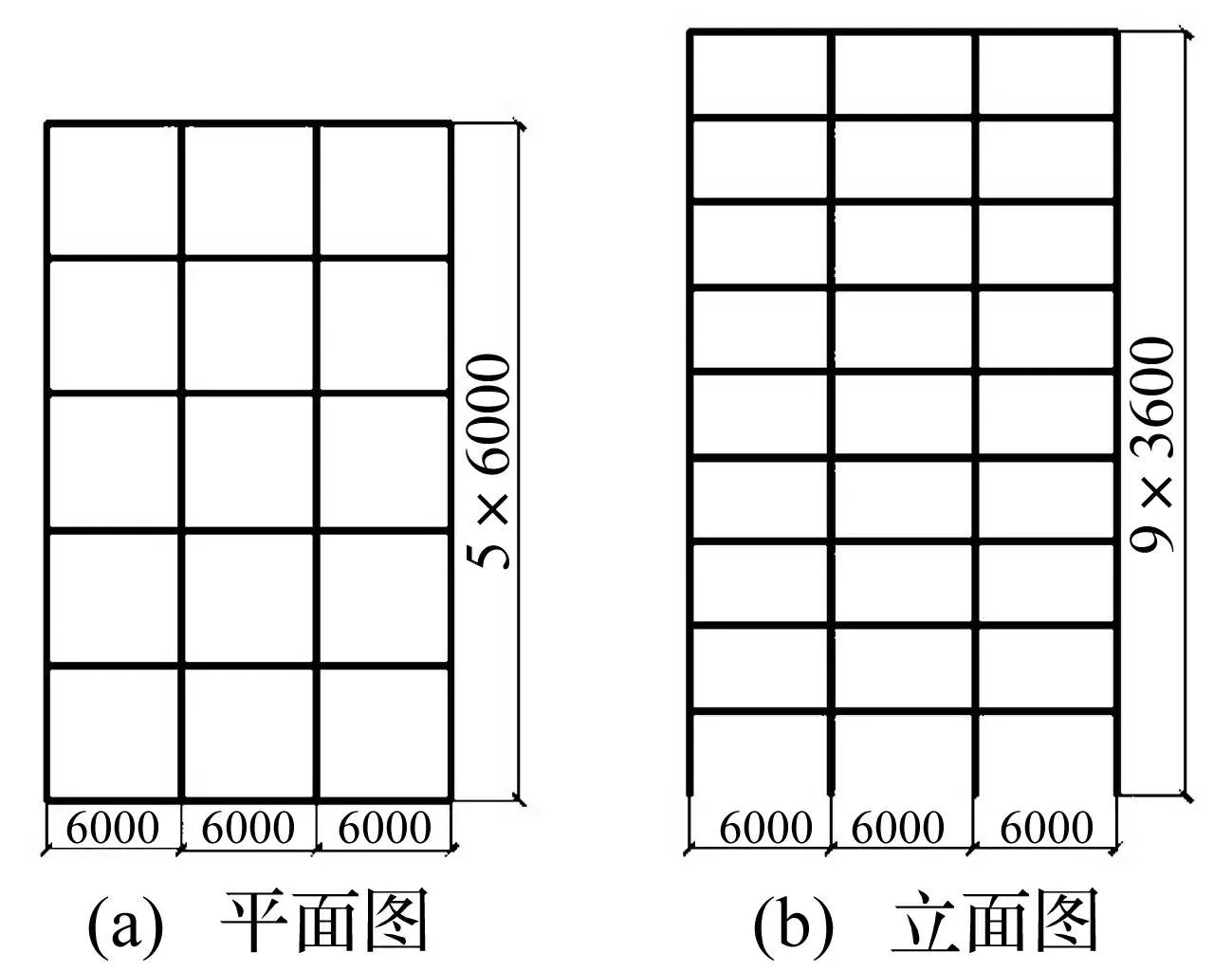
图2 9层钢框架模型 Fig.2 9 Floors steel frame model

楼层柱截面梁截面1~3□380×380×22H600×200×11×174~6□380×380×20H600×200×11×177~9□380×380×17H600×200×11×17
3.3地震波选取
参考ATC-63选波原则[12],在PEER强震数据库中选20条满足波速范围及震中距要求的地震记录为IDA地震输入,见表4。

表4 所选地震动记录
3.4在役钢框架结构易损性分析结果
以北京地区为例,Q235钢材年锈蚀深度为11.7 μm/a[13],采用ANSYS有限元分析软件对钢框架5个龄期分别进行弹塑性时程分析,获得结构在不同龄期、不同地震作用下的 IDA 曲线,取β=1,回归分析建立5个不同龄期结构地震需求为
(18)
式中:下标数字表示结构龄期;PGA单位为g。

图3 考虑多龄期的钢框架易损性曲线 Fig.3 Aging considerations in fragility curves of steel frame
将5个不同龄期结构地震需求分别代入结构特定阶段的失效概率函数,获得结构5个不同龄期、4种不同性态水平下地震易损性曲线见图3。由图3看出,4种性能水平下,结构失效概率均随龄期增加而增大。龄期越长,结构失效概率增量越大。如结构中度损伤阶段,PGA为0.5 g、龄期为25年时结构失效概率较0年增大2%;龄期50年时结构失效概率较25年时增大3%;龄期75年时结构失效概率较50年时增大5%;龄期为100年时结构失效概率较75年时增大6%。

表5 不同龄期所对应的PGA平均值与对数标准差
结构在5个不同龄期、4种不同破坏水平对应的PGA平均值m(t)与对数标准差n(t)见表5。由表5看出,4种不同破坏水平对应的PGA平均值与对数标准差均随龄期增长逐渐减少,说明结构龄期越长,失效概率逐渐增大。
为更直观反映结构全寿命周期内龄期对结构失效概率影响,令
m(t)=m1t2+m2t+m3
(19)
对5个不同龄期、4种不同破坏水平对应的结构失效概率为50%的PGA平均值数据进行多项式拟合,所得结构4种不同破坏水平下随龄期的连续失效概率曲面见表6、图4。

表6 连续失效概率函数的多项式系数

图4 不同损伤指数下考虑龄期的结构易损性曲面 Fig.4 Different damage index of vulnerability surface of the structure under the age
4结论
本文考虑钢材锈蚀对结构抗震性能影响,建立梁柱焊接钢框架的损伤模型与全寿命地震易损性模型,结论如下:
(1)提出基于首超变形和累积塑性转角的双参数构件损伤模型,考虑构件与层权重系数建立结构整体损伤模型,并定义结构4种破坏状态。
(2)研究锈蚀对钢材的力学性能的影响,建立钢材多龄期本构。引入时间参数,通过多龄期考虑不同锈蚀率对钢材力学性能影响,概念清晰,物理意义明确。
(3)为研究不同使用寿命结构的抗震性能,考虑钢材锈蚀对整体结构影响,建立的梁柱焊接钢框架全寿命地震易损性评估模型可为该类结构的地震灾后快速损失评估与预测方法提供参考。
(4)以6层梁柱焊接钢框架为例,5个龄期、4种性能水平下结构易损性曲线表明,随龄期增长,结构失效概率增量逐渐增大,且龄期对结构失效概率影响随损伤程度增加而增大。
(5)通过二次曲线回归拟合4种不同破坏水平对应的PGA平均值及对数标准差与龄期关系,建立结构随龄期变化的连续失效概率函数,获得结构失效概率随龄期变化规律。
参考文献
[1]Choe D E,Gardoni P,Rosowsky D,et al. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion[J]. Reliability Engineering System Safty,2008,93(3):383-393.
[2]李吉涛,杨庆山,刘阳冰.多点地震激励下大跨连续钢构桥易损性分析[J].振动与冲击,2013,32(5):75-80.
LI Ji-tao, YANG Qing-shan, LIU Yang-bing. Fragility analysis of long span continuous rigid frame bridge under multi-support excitations[J].Journal of Vibration and Shock,2013,32(5):75-80.
[3]Park Y J,Ang A. Mechanistic seismic damage model forreinforced concrete[J]. Journal of Structural Engineering, 1985,111(4) :740-756.
[4]Bojórquez E,Reyes-Salazar A. Energy-based damage index for steel structures [J]Steel and Composite Structures, 2010,10(4):343-360.
[5]Castiglionia C A, Pucinotti R. Failure criteria and cumulative damage models for steel components under cyclic loading[J].Journal of Constructional Steel Research, 2009, 65: 751-765.
[6]杜修力,欧进萍.建筑结构地震破坏评估模型[J]. 世界地震工程, 1991, 7(3): 52-58.
DU Xiu-li,OU Jin-ping. Seismic damage evaluation model of building structures[J].World Earthquake Engineering, 1991,7(3):52-58.
[7]史炜洲. 钢材腐蚀对住宅钢结构性能影响的研究与评估[D].上海:同济大学,2009.
[8]Lee H S,Noguchi T,Tomosawa F.FEM analysis for structure performance of deteriorated rc structures due to rebar corrosion[C].Prodceedings of the International Concrete under Several Conditions,1998.
[9]Cornell C A,Jalayer F, Hamburger R O,et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of Structural Engineering,2002,128(4):526-533.
[10]Sucuoglu H, Yucemen S,Gezer A,et al. Statistical evaluation of the damage potential of earthquake ground motions[J]. Structural Safety,1999,20(4): 357-378.
[11]HAZUS99, user’s manual[S]. Washington D C: Federal Emergency Management Agency, l999.
[12]ATC-63,quantification of building seismic performance factors[S]. FEMA P695,2008.
[13]刘新,时虎. 钢结构防腐蚀和防火涂装[M].北京:化学工业出版社,2005.


