土-结构非线性相互作用混合约束模态实施方法
第一作者姜忻良男,博士,教授,博士生导师,1951年生
邮箱:jiangxinliang@126.com
土-结构非线性相互作用混合约束模态实施方法
姜忻良,张海顺
(天津大学建筑工程学院滨海土木工程结构与安全教育部重点实验室,天津300072)
摘要:分析、探讨线性-非线性混合约束模态综合法用于土-结构相互作用的动力分析实施方法。据结构存在局部非线性特性,提出对整体结构划分为若干个线性、非线性子结构,对线性子结构只需一步提取特性矩阵并进行方程降阶,而对非线性子结构则逐步提取降阶后的等效特性矩阵。通过组装各子结构达到对整体结构特性矩阵的降阶处理。对非线性子结构凭借在小段时间Δt内利用分段等效线性化手段,通过ANSYS二次开发工具UPFs编辑写成可执行程序文件,并与MATLAB联立计算,实现特性矩阵提取。结果表明,该方法求得结构的各阶频率和动态响应时程曲线与ANSYS直接计算吻合良好。可逐步提取等效弹塑性特性矩阵,为采用变化的特性矩阵对结构进入塑性阶段深层次分析研究提供有效方法。
关键词:土-结构相互作用;约束模态综合法;势能判据截断准则;局部非线性;弹塑性刚度矩阵
收稿日期:2013-11-08修改稿收到日期:2014-03-31
中图分类号:TU317.1文献标志码:A
基金项目:国家“863”计划资助项目(2013AA040103);河南省高等学校精密制造技术与工程重点学科开放实验室开放基金资助(PMTE201308A)
Mixed constraint modal method for nonlinear soil-structure interaction
JIANGXin-liang,ZHANGHai-shun(School of Civil Engineering, Tianjin University/Key Laboratory of Coastal Civil Engineering Structure and Safety, Ministry of Education, Tianjin 300072, China)
Abstract:Here, the implementation technique of the linear-nonlinear mixed constraint modal synthesis method was analyzed for soil-structure dynamic interaction. According to the local nonlinear feature, the whole structure was divided into several linear and nonlinear sub-structures. Those linear sub-structures just required only one step to extract the characteristic matrices and reduce equation order, while for nonlinear sub-structures, they needed step by step to extract the reduced order equivalent characteristic matrices. By assembling the above sub-structures, the order of the whole structural characteristic matrix was reduced. For the nonlinear sub-structures, using the piecewise equivalent linearization method within a small time interval Δt, an executable program file to extract the characteristic matrices was edited by means of ANSYS secondary development tools UPFs and the simultaneous computation was done with MATLAB. Results show that the modal frequencies and dynamic response time history curves obtained with the above method agree well with those obtained with ANSYS direct calculation; using this method can extract the equivalent elastic-plastic feature matrices step by step, and it provides an effective tool for further studying the plastic phase dynamic analysis of structures with time-varying characteristic matrices.
Key words:soil-structure interaction; constrained modal synthesis method; potential energy mode cut-off criterion; local nonlinear; elastic-plastic stiffness matrix
解决地基土-结构动力相互作用(SSI)问题时,有限元法为离散化强有力工具,但因其自由度太多致直接求解十分困难。尤其三维问题,结构越复杂,自由度数越多,即便用人工边界适当减小土体区域范围,仍会耗费大量计算成本。因采用有限元技术进行动力分析时需进行结构各单元特性矩阵总装,导致整体矩阵庞大,一般微机难以满足计算要求。因此可借助划分动态子结构方法,利用约束模态综合法实现方程降阶,为利用微机进行大型结构有限元动力分析提供了可行、经济手段。而方程降阶仅适用于线弹性结构,对非线性弹塑性结构则不适用。
本文基于动态子结构法中约束模态综合法(CMS)与势能判据截断准则,据土-结构相互作用模型存在局部非线性特性,提出将整体结构划分为若干线性子结构、非线性子结构,对线性子结构只需一步提取特性矩阵并进行方程降阶,而对非线性子结构则逐步提取其等效特征矩阵,通过组装子结构达到对整体结构特性方程降阶处理,继而对地基土-结构相互作用模型进行特征值方程计算及动力时程有限元分析,并将计算结果数值曲线与有限元直接法对比,分析所提方法的高效可行性。
1基本理论及方法阐述
动态子结构法理论基础为Rayleigh-Ritz法,是缩减自由度的有效方法,其将大型复杂结构划分为若干子结构,分析研究每个子结构的动力特性,并利用经验手段或理论方法确定其保留的低阶主要模态信息,再据每个子结构交界面的协调关系组装成整体结构的动力特性。此方法用于分析较少自由度的整体结构,使大型复杂结构整体动力特性问题得以解决。对采用何种经验手段或理论方法确定其保留的低阶主要模态信息既能满足工程需求又可靠性高问题,姜忻良等[1]在基于动态子结构法中约束模态综合法下提出势能判据截断准则进行子结构主模态截断,并推论验证由各子结构势能范数随截取主模态阶数变化曲线判断,当截取阶数取合适值时,子结构势能将趋于收敛,即为最佳子结构截取阶数。
动态子结构法与势能判据截断准的建立则均基于振型叠加法基础,该类方法仅适合求解线性结构系统动力问题,使动态子结构法对非线性结构体系进一步应用受到限制。研究表明,大量实际工程中整体结构在外部荷载作用下并非全部构件都进入非线性阶段,而仅在某些区域才出现非线性特征,即结构存在局部非线性特点。同样土-结构相互作用体系在地震动激励下也存在局部非线性区域特点。在地震响应分析问题中,仅与上部结构邻近地基土区域会产生塑性应变,而远离上部结构的地基土区域在整个加载过程中始终处于线性阶段。故考虑利用线性-非线性混合约束模态综合法,将原不易进入非线性阶段区域划分成若干线性子结构,再利用势能判据截断准则缩减自由度,而不必在整体结构模型中反复迭代计算;而对非线性子结构通过改变其各单元本构关系方法将其等效为线性子结构,通过所有子结构合并计算求解整体非线性动力学方程,用较小计算成本获得非线性体系既满足工程应用且较精确的动力解。
2结构刚度矩阵提取方法
用商业软件进行各种结构动、静力分析可据不同目的提取刚度、质量、阻尼及荷载矩阵,以便利用各类矩阵做后期分析与处理。对线弹性结构可利用编程提取,方法较简单;但对非线性弹塑性结构各类矩阵提取较困难,大型商业软件一般无直接提取方法。致采用变化的结构特性矩阵研究结构某些阶段乃至整个阶段受力特点造成困难。本文利用ANSYS二次开发工具尝试进行特性矩阵提取编程,其中刚度矩阵提取为关注重点。
在ANSYS有限元程序中提取整体刚度矩阵方法主要是HBMAT命令法及超单元(Super-element)法。HBMAT命令为ANSYS提取整体刚度矩阵的直接内部提取方法,但其仅适用于线弹性分析,不适用非线性分析,且该命令采用索引存储方法的稀疏矩阵并以Harwell-Boeing格式存储刚度矩阵下三角非零数据,并需后期借用MATLAB等程序编写命令处理还原其矩阵形式。同时HBMAT命令法也有严重不足,即形成的刚度矩阵无序,对不同结构单元网格较推算出矩阵某行某列的值与哪个节点自由度相关,且不能说明整体刚度如何从单元刚度矩阵对号入座组装的,而此过程恰为关注内容。超单元法同样仅可提取线弹性整体刚度矩阵,基本步骤为,创建有限元模型并施加约束、定义分析类型为子结构、定义输入何种矩阵、选择并定义所有节点为主自由度、求解并列出矩阵。所列整体刚度矩阵为全部元素(全矩阵),按行顺序分别列出各列元素数值,但结构节点较多时,其数据量庞大,且后期提取数据需大量人工处理,非常繁琐导致不方便使用。
由于HBMAT命令法及超单元法在提取整体刚度矩阵的应用上均有不便之处,故本文基于FORTRAN语言的UPFs二次开发工具在ANSYS有限元程序中提取矩阵。其核心思想为通过编写外部用户程序从ANSYS子空间计算方法模态分析结果File.Full的二进制文件中提取特性矩阵各行、列非零值,编写MATLAB程序按节点编号由小到大顺序对号入座组装形成完整矩阵形式。ANSYS二次开发环境为Compaq Fortran 6.5,其中主文件为Matrix-extraction. For,其余Matrix-output.F90用于矩阵输出,Binlib.Lin为ANSYS提供库文件,Binlib.Dll为动态链接库文件。运行编译后形成可执行Matrix-output.Exe文件即获得质量矩阵(Mass.Matrix)、刚度矩阵(Stiffness.Matrix)文件。

3非线性等效刚度矩阵处理方法
考虑结构在非线性塑性阶段提取各时刻刚度矩阵,可近似认为该非线性塑性本构关系由分段逐步递减且在小段Δt时间内线性本构关系组合。对进入非线性阶段结构,在小段Δt时间内提取t及t+Δt时刻各单元节点应力应变。以2D平面应变问题为例进行推导,每个单元每个节点平面应变的物理方程为
t时刻
(1)
t+Δt时刻
(2)
则Δt时段应变差为
(3)
式(3)为各向同性的物理方程。若为提取刚度矩阵修改E,G则变成各项异性,物理增量方程应为
(4)
式(4)可简化为
(5)
(6)

ANSYS每时刻Step运行结束后调用MATLAB程序时须设置只有在该Step调用的MATLAB程序分析完成后才可继续运行ANSYS程序,即ANSYS在调用MATLAB程序未计算完毕时,须等待而不能继续进行运算。需两者同时运行并建立Flag文件,通过两者中读其内容判断对方是否运行。两者若运行完一个Step,改变Flag,告诉对方自己当前运行结束,对方可继续运行,否则必须等待。
4局部非线性SSI体系的CMS应用
为检验局部非线性下约束模态综合法及势能判据截断准则的有效性,拟对地基土-高层剪力墙结构相互作用体系进行动力分析。计算模型见图1。上部为10层剪力墙结构,层高3.6 m,宽24 m;支撑于2层箱型基础上。土体设为分层土,地质参数见表1。土体区域沿承台两侧宽度各取100 m,沿深度取30 m。框架剪力墙与箱型基础阻尼比为0.05,土阻尼比设为0.2。结构模型两端自由端,底端固定端。对整体结构进行Taft波、EL-centro波及天津人工波动力时程分析。篇幅所限,以天津人工波为例进行分析。图2为ANSYS直接计算法中地震波作用下其下部土体塑性区变形云图,表现出局部非线性特性。为比较约束模态综合法的优越性及精确度,将计算结果与ANSYS直接计算法进行对比分析。
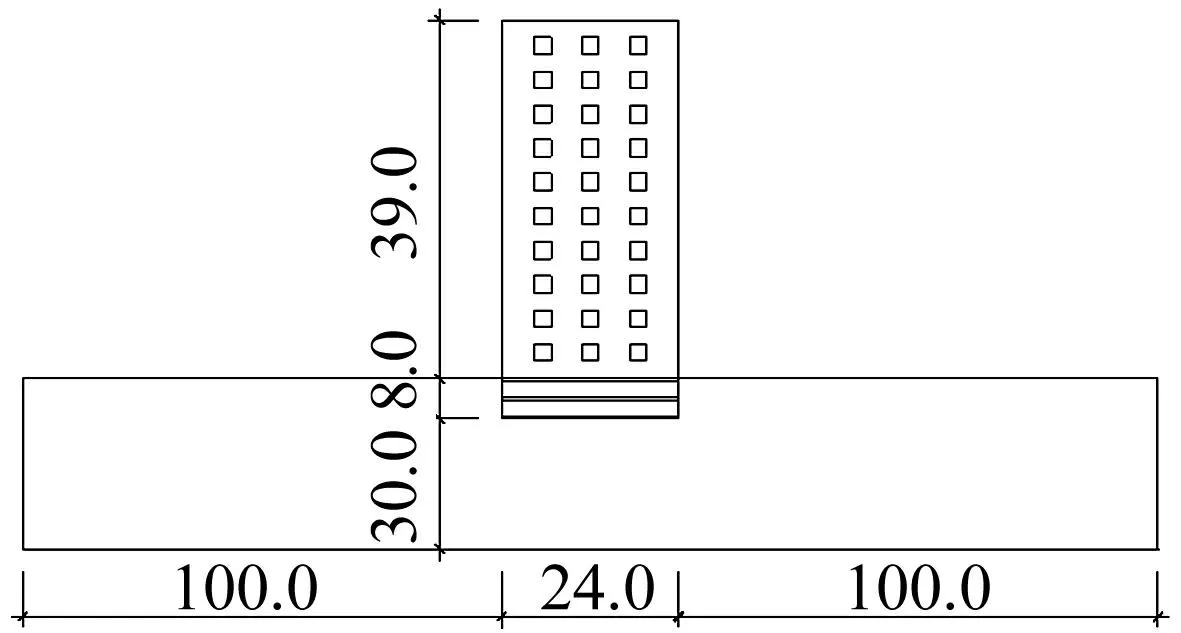
图1 地基土-高层剪力墙结构体系计算模型 Fig.1 Calculation model of soil-structure interaction system

编号厚度/m弹模/Pa泊松比μ粘聚力/Pa摩擦角Φ/(°)湿容重/(kg·m-3)17.12.00E70.21425014.51940212.03.48E70.21613917.31915310.95.00E70.21850023.92036

图2 地震波作用下整体模型塑性区变形云图 Fig.2 Von misis equivalent plastic strain contour
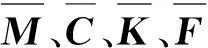

图3 子结构示意图 Fig.3 Substructure division

图4 子结构1截断参数判定 Fig.4 Substructure 1 truncation parameter determination
本文采用逐步提取刚度矩阵法可方便地通过不同时刻特征值方程求得结构频率变化趋势。图8为天津人工波作用下整体结构前5阶频率变化过程。由图8看出,结构在弹性阶段频率保持不变,进入塑性阶段时呈阶梯状降低。
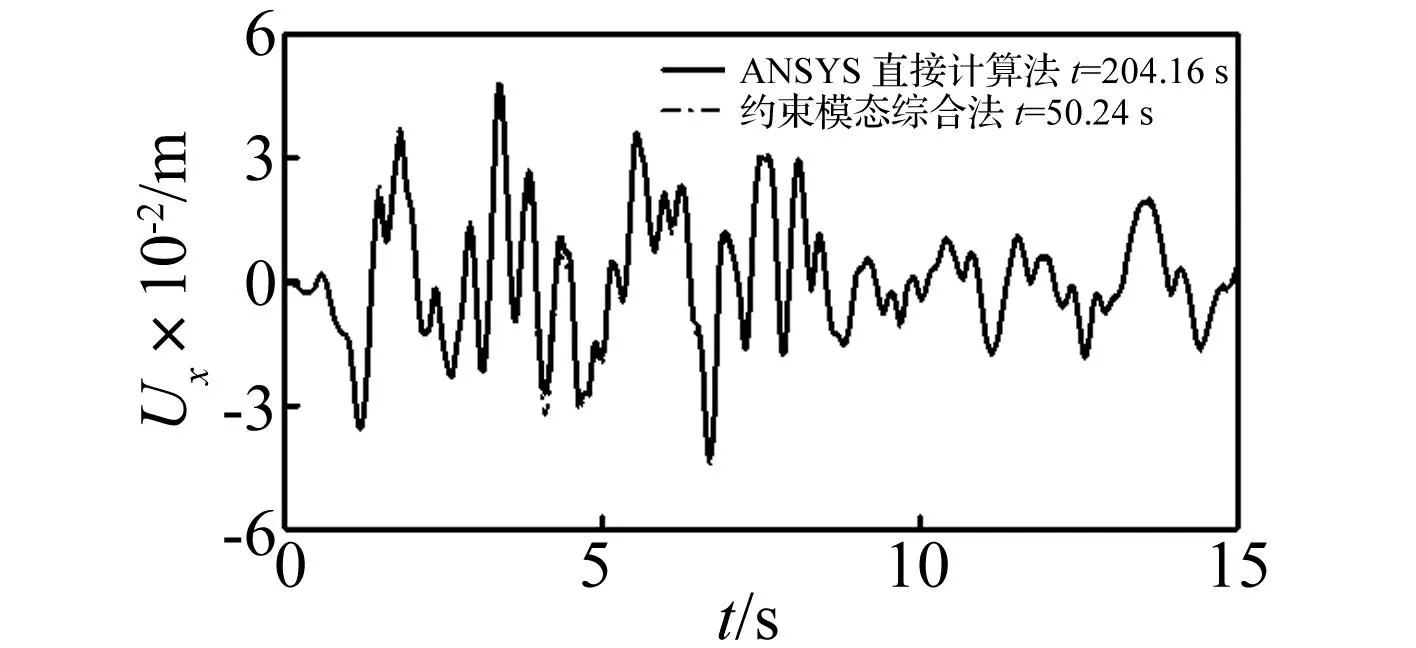
图5 位移时程曲线对比 Fig.5 Displacement curve comparison


图6 速度时程曲线对比Fig.6Velocitycurvecomparison图7 加速度时程曲线对比Fig.7Accelerationcurvecomparison图8 地震波作用下前3阶频率变化曲线Fig.8First3orderfrequencycurvesunderearthquakeaction
天津人工地震波动力非线性分析前3阶频率在整个过程的某些时间点变化见表2,可见当地震波达到峰值时基频降低程度最大,趋于平稳时各阶频率保持恒定。

表2 各阶频率变化情况 (Hz)
5结论
(1)本文据土-结构相互作用存在局部非线性特点用线性-非线性混合约束模态综合法进行分析。结果表明,用该方法与有限元直接法所得响应曲线基本吻合,验证了在弹塑性阶段利用分段等效线性化手段及ANSYS二次开发程序文件提取矩阵的正确性与可行性。与有限元直接法相比,其计算成本大幅度降低,是求解土-结构动力相互作用问题的有效方法。
(2)本文方法在分析过程中对局部非线性部分提取刚度、质量、阻尼矩阵为采用变化的特性矩阵对结构进入塑性阶段深层次分析研究提供有效方法。
参考文献
[1]王菲. 地基土-高层建筑相互作用的动态子结构法[D].天津:天津大学,2010.
[2]白建方, 楼梦麟. 基于动力子结构方法的场地地震反应分析方法[J]. 震灾防御技术, 2008,3(2):145-154.
BAI Jian-fang, LOU Meng-lin. The dynamic sub-structure method for seismic response of irregular topography[J]. Technology for Earth-quake Disaster Prevention, 2008, 3(2):145-154.
[3]曲哲, 叶列平. 计算结构非线性地震峰值响应的等价线性化模型[J]. 工程力学, 2011,28(10):93-100.
QU Zhe, YE Lie-ping. An equivalent linear model to estimate maximum inelastic seismic responses of structural systems[J]. Engineering Mechanics,2011, 28(10) :93-100.
[4]闫相桥, 杜善义, 王铎. 材料非线性有限元分析中组织结构刚度阵的子结构法[J]. 哈尔滨工业大学学报,1989,12(6): 100-103.
YAN Xiang-qiao, DU Shan-yi, WANG Duo. An effective method of assembling the structural stiffness matrix in material nonlinear finite element analyses[J]. Journal of Harbin Institute of Technology,1989,12(6):100-103.
[5]柳国环, 陆新征. 基岩地震谱与地震动位移输入的土-结构相互作用(SSI)计算模型改进[J]. 岩石力学与工程学报, 2011,30(5):84-89.
LIU Guo-huan, LU Xin-zheng. Spectra of bedrock earthquake motion and improvement of soil-structure interaction(SSI) calculation model for seismic displacement inputting[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(5):84-89.
[6]应祖光, 叶淑琴, 金林. 基于固定界面子结构模态的频响函数精确综合法[J]. 振动与冲击,2010,29(3):132-133.
YING Zu-guang, YE Shu-qin, JIN Lin. Exact frequency response function synthesis method using interface fixed substructure modes[J]. Journal of Vibration and Shock, 2010, 29(3):132-133.


