利用数学技巧处理斜面上的平抛运动

缪志兴

【中图分类号】G633.7 【文献标识码】A 【文章编号】2095-3089（2015）12-0162-01

高中物理是一门综合性比较高的学科，尤其是与数学学科的交叉应用比较多，大量应用到一些数学中的处理技巧与方法。应用数学处理物理问题的能力是高考考纲所列的五种能力之一，学生利用数学知识研究物理问题也是高考考查的重点内容。本文以斜面上的平抛运动为例，让学生体会数学在物理中的应用。

例：从倾角为θ的斜面上A点，以初速度V0沿水平方向抛出一个小球，落在斜面B上，求：从抛出到落到斜面上时，小球离斜面的最远距离。

【解法一】平抛运动的基本公式和推论

从抛出点开始计时，经过时间t小球与斜面的距离最在；如图1所示，当小球的速度V与斜面平行时，小球离斜面距离达到最远，即此时速度与水平面的夹角为θ。此时=tanθ=，则t=

作速度的反向延长线，交初速度方向的延长线交于M点，根据平抛运动的结论：M点为水平位移的中点，所以，小球距离斜面的最大距离：

MN=AMsinθ=sinθ=v0tsinθ=v0sinθ=

【解法二】运动的分解

如图2所示，将平抛运动的初速度v0和加速度g沿着斜面和垂直于斜面分解，在垂直于斜面方向vx=v0 sinθax=gcosθ小球做匀变速直线运动，平行于斜面方向vx=v0cosθ vy=v0sinθ小球做匀加速直线运动。

所以，当小球在垂直于斜面方向的速度减为0的时，小球距离斜面最远。

hmax==

【解法三】解析几何法

（1）切线方程法

由于做平抛运动的小球的数学解析式为：x=vot y=gt则做平抛运动的小球的解析式为： y0=同理可设斜面0A的解析式为y1=xtanθ

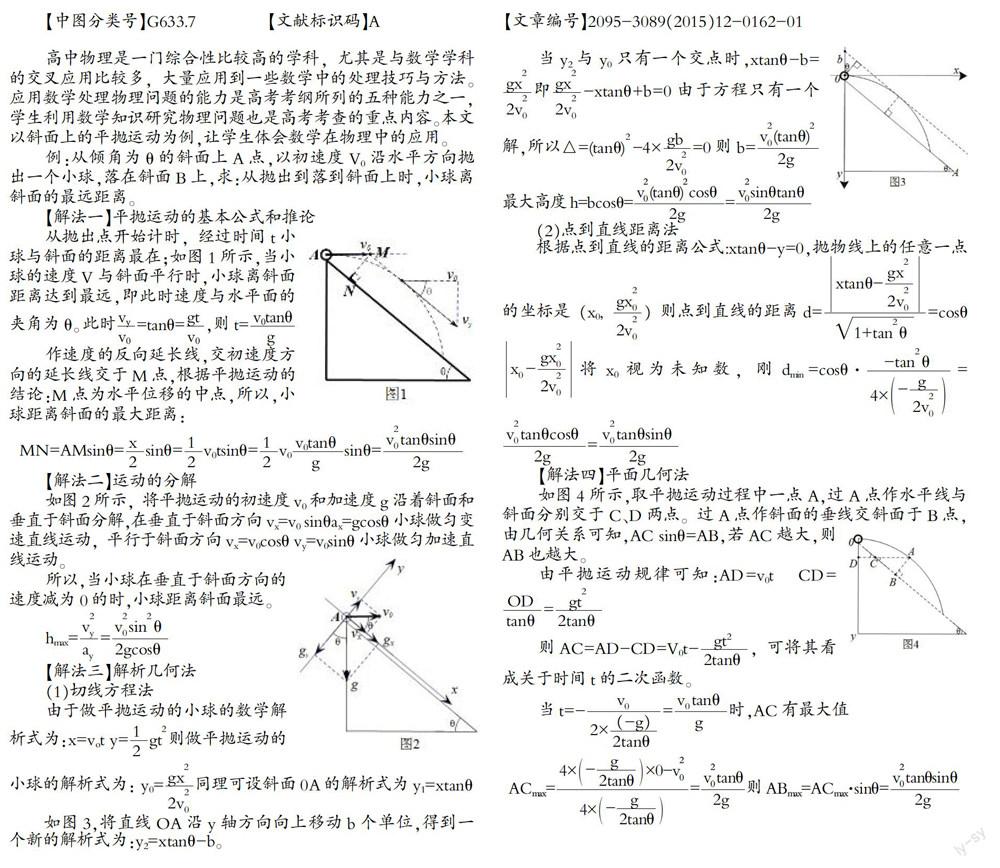
如图3，将直线OA沿y轴方向向上移动b个单位，得到一个新的解析式为：y2=xtanθ-b。

当y2与y0只有一个交点时，xtanθ-b=即-xtanθ+b=0由于方程只有一个解，所以△=（tanθ）-4×=0则b=最大高度h=bcosθ==

（2）点到直线距离法

根据点到直线的距离公式：xtanθ-y=0，抛物线上的任意一点的坐标是（x0，）则点到直线的距离d==cosθx-将x0视为未知数，刚dmin=cosθ·==

【解法四】平面几何法

如图4所示，取平抛运动过程中一点A，过A点作水平线与斜面分别交于C、D两点。过A点作斜面的垂线交斜面于B点，由几何关系可知，AC sinθ=AB，若AC越大，则AB也越大。

由平抛运动规律可知：AD=v0t CD==

则AC=AD-CD=V0t-，可将其看成关于时间t的二次函数。

当t=-=时，AC有最大值

ACmax==则ABmax=ACmax·sinθ=