分件供送变距螺杆的三维实体建模与性能分析

欧阳虎，黄运板

（广东工业大学 机电工程学院，广东 广州 510006）

0 引言

分件供送螺杆是现代包装机械行业常用的一种供送装置，可按照包装工艺的要求，将不同外形的包装容器逐个输送到相应包装工位，因此分件供送螺杆被称为整个设备的“咽喉”，其结构与性能直接影响到整个设备的作业质量、工作效率、总体布局和自动化水平。合理地设计分件供送螺杆的结构，可以减轻供送过程中的冲击、振动、卡滞等现象［1］，从而提高变距供送螺杆的输送稳定性，对实现供送件的可靠传送具有现实意义。现在普遍采用的螺杆螺旋线形式有三段组合式、代数多项式螺旋形、最小二乘法曲线拟合等［2－5］。但是这些螺旋线不仅设计过程繁琐，而且制造的螺杆往往在工作过程中运行不平稳。因此本文采用四段组合式螺旋形的数学模型，使用精确的解析作图法绘制螺旋槽，并利用CATIA强大的扫描混合功能建立其三维实体模型，最后基于Ansys Workbench对螺杆进行模态分析，以得出一些对现实设计有指导作用的结论。

1 螺杆螺旋线的数学模型

合理确定螺杆螺旋线的形式，是保障螺杆运行过程中物件平稳供送的关键。在螺杆起始段，为了使供件平稳进入螺杆，采用等螺距实现等速供送；在第二段，螺杆的供送加速度依照正弦函数由零增至最大，为正弦变加速度段；在第三段，供件在最大加速度状况下加速运动，以便快速增大供件的速度与间距，为等加速度段；在最后段，螺杆的供送加速度依余弦函数由最大减至零，以便减小供件出螺杆时的冲击，最终使供件与星轮同步，为余弦减加速度段。以上即为本文所采用的四段组合式螺旋线形式，如图1所示。

图1 四段组合式螺杆结构示意图

（1）等速段的运动规律方程为：

（2）正弦加速段的运动规律方程为：

（3）等加速段的运动规律方程为：

（4）余弦加速段的运动规律方程为：其中：ak、vk、Hk分别为螺杆各段曲线的加速度、速度和位移，k＝1、2、3、4，分别对应等速段、正弦加速段、等加速段和余弦加速段；s0为螺杆初始螺距值；n为螺杆转速；amax为螺杆的最大加速度；ik、ikm分别为螺杆各段曲线的圈数及最大圈数。

以上数学模型是变距螺杆设计的理论基础，将该数学模型导入CATIA中可生成螺杆的变距螺旋线。

2 螺旋槽的数学模型

螺杆工作时螺旋槽对供件起着隔挡、增减速推移和稳定供送的作用，准确的螺旋槽设计对螺杆工作性能的提升至关重要。本文通过分析圆柱形瓶与螺杆的相贯运动原理，建立了圆柱形瓶变距螺杆螺旋槽的数学模型。供件与螺杆的相贯运动分析简图如图2所示。

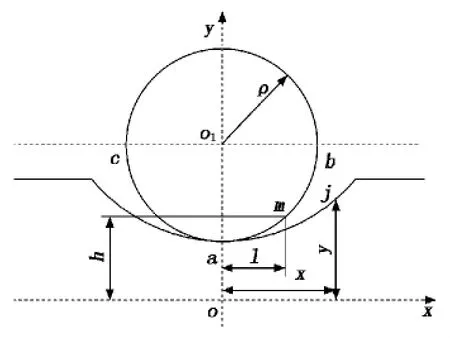
图2 供送件与螺杆相贯运动分析简图

根据图2设圆上ab段任一点m坐标为（l，h），其中0≤l≤ρ，ρ为圆形瓶半径。根据相贯运动原理可求得m点的相贯线轨迹j（x，y）的坐标为：

其中：s为各段螺旋的设计螺距值；r0为螺杆内半径。取螺杆外径D＝100mm，内半径r0＝30mm，瓶的半径ρ＝30mm，初始螺距s0＝65mm，则起始段的螺旋槽形状如图3所示。其他段的螺旋槽形状根据以上方法依次可以获得。

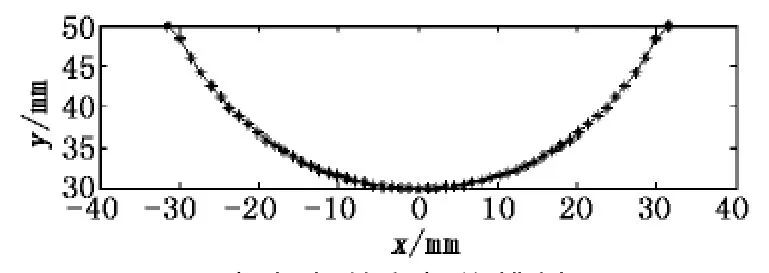
图3 螺杆起始段螺旋槽剖面图

3 变距螺杆的三维实体建模

在CATIA中变距螺杆的三维实体建模［6］步骤如下：

（1）创建实体旋转特征。

（2）建立参数并在fog中创建各段螺旋线的规则曲线。根据螺杆螺旋线数学模型，选取相应参数，最终生成曲线如图4所示。

（3）创建多截面实体。由式（5）可知，螺旋槽的截面随螺距s的变化而变化，因此螺旋槽的各个截面尺寸都是不同的。采用CATIA的多截面实体功能可以很方便地实现螺杆的三维实体建模。

（4）修剪及倒角，最后生成的四段式变距螺杆三维模型如图5所示。

图4 螺杆螺旋线

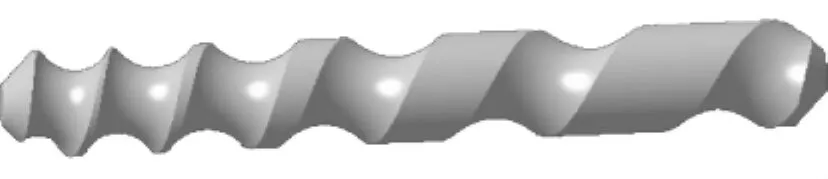
图5 四段式变距螺杆三维实体模型

在考虑一定约束条件的情况下设计三段式（等速段、正弦加速段、等加速段）变距螺杆，两种螺旋线螺杆的总长度一致，螺杆末段的螺距相等，被供送件出螺杆时速度相等。本文选取螺杆总长度L＝800mm，螺杆末段螺距s＝300mm，被供送件出螺杆时速度v＝0.8 m/s。最终生成的三段式变距螺杆三维实体模型如图6所示。

图6 三段式变距螺杆三维实体模型

4 在ANSYS Workbench中对两种螺旋线螺杆进行分析

分件供送螺杆材料选为Nylon，其密度为1 145 kg/m3，弹性模量为2.83GPa，泊松比为0.4。

4.1 不考虑预应力和挤压应力的作用时

将生成的CATIA实体模型导入的ANSYS Workbench的modal模块中［7］，此时不考虑螺杆在装配和工作时所受拉伸、挤压和弯矩的作用，仅在螺杆两端施加固定约束，并对螺杆进行网格划分。四段式螺杆网格划分如图7所示。

图7 四段式螺杆网格划分

对四段式螺杆进行分析，得到的前6阶模态分析［8］结果如图8所示。

用同样的方法对三段式螺杆进行模态分析，得到其前6阶振型结果，并将两种螺杆分析结果列在表1中。

根据表1中的数据可知，在不考虑预应力作用时三段螺旋线螺杆和四段螺旋线螺杆的各阶固有频率相差不大，四段螺旋线螺杆的各阶固有频率略高于三段螺旋线螺杆相应的各阶固有频率。

4.2 考虑预应力和挤压应力的作用时

先在ANSYS Workbench的静力分析模块中对螺杆施加一个5rad/s的自转转速，然后沿螺杆轴向施加一个大小为300N作用力，模拟螺杆所受外力。再将上述受力模型导入ANSYS Workbench的Modal模块中重新进行分析，得到的三段螺旋线螺杆和四段 螺旋线螺杆分析结果如表2所示。

图8 静态时四段螺旋线式螺杆模态分析结果

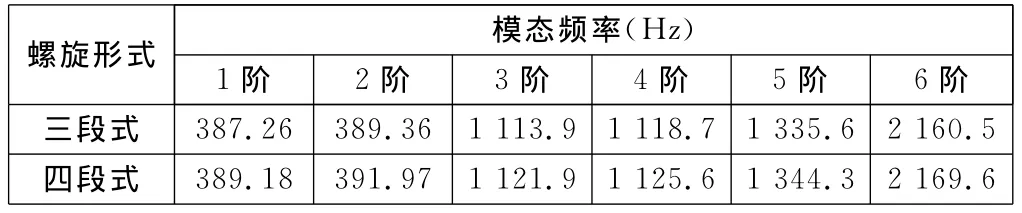
表1 不考虑预应力作用时两种螺杆的模态分析结果

表2 考虑预应力作用时两种螺杆的模态分析结果

由表2可知，在考虑预应力作用的情况时四段螺旋线式螺杆的各阶振型固有频率明显高于三段螺旋线式螺杆。

5 结论

将建立的两种螺杆导入分析软件ANSYS Workbench中进行模态分析，分析结果表明，螺旋线的分布形式对静态下螺杆的固有频率影响不大。相对于静止状态，工作状态下两种螺杆的各阶固有频率明显降低，但是四段螺旋线式螺杆的各阶固有频率明显高于三段螺旋线式螺杆相应的各阶固有频率，因此，四段螺旋线式螺杆在抗振方面的性能明显高于三段螺旋线式螺杆。

［1］吴其叶.高速分件供送螺杆动力特性的分析研究［J］.包装与食品机械，2003（6）：6－8.

［2］许林成.包装机械原理与设计［M］.上海：上海科学技术出版社，1988.

［3］周向新.高速分件供送螺杆全程单函数运动规律及特性分析［J］.包装与食品机械，1996（1）：4－9.

［4］余雷.最小二乘法拟合变导程螺杆螺旋曲线［J］.机电工程，1999（3）：5－6.

［5］孔伟时.输送圆柱形容器的变螺距螺杆加工问题探讨［J］.中国包装业，2003（5）：33－35.

［6］张磊，徐昌贵，仉毅.基于Pro/E的分件供送螺杆的造型设计［J］.包装工程，2008，28（5）：70－72.

［7］陈艳霞，陈磊.ANSYS Workbench工程应用案例精通［M］.北京：电子工业出版社，2012.

［8］蔡力钢，马仕明，赵永胜，等.多约束状态下重载机械式主轴有限元建模及模态分析［J］.机械工程学报，2012（3）：348－354.