水平井体积压裂缝网表征及流动耦合模型

贾 品, 程林松, 黄世军, 田虓丰（.中国石油大学（北京）石油工程学院,北京 049；.中海油研究总院,北京 0007）

水平井体积压裂缝网表征及流动耦合模型

贾 品1, 程林松1, 黄世军1, 田虓丰2
（1.中国石油大学（北京）石油工程学院,北京 102249；2.中海油研究总院,北京 100027）

针对岩石脆性系数高且发育天然裂缝的储层,提出表征水平井体积压裂形成裂缝网络的三种基本模式,并将渗流过程划分为油藏流动和缝网内部流动.在此基础上,利用势叠加原理导出油藏流动控制方程,利用有限差分方法建立缝网内部有限导流等式；其次,采用星三角变换法处理人工缝与天然缝的交汇流动；最后,耦合两部分流动矩阵方程得到水平井体积压裂缝网渗流数学模型.该模型表明：当水平井改造段长度一定时,压裂段数与段内分簇数是决定产能的最主要因素,其次是人工裂缝半长和人工缝导流能力,而天然裂缝密度和导流能力对产量影响较小.实例应用表明,实际产油量与模型计算值一致,误差较小.

体积压裂水平井；裂缝网络；定量表征；星三角变换法；耦合流动；产能

0 引言

目前,对于低孔隙度、低渗透、低压等因素所导致的低产储层,一般采取压裂措施产生多裂缝以提高产量[1].当储层岩性脆性较高并发育天然裂缝时,水平井经分段多簇体积压裂后,通常在近井地带形成复杂裂缝网络的改造区[2].改造区内的裂缝网络系统以主裂缝为主干,并与多级次生裂缝及天然裂缝纵横交错[3].其中,裂缝网络大小、裂缝密度以及导流能力都是影响压裂后产能的主控因素[4].本文基于国内外学者对水平井体积压裂缝网的研究,一方面尝试用较为简单的方法来表征缝网；另一方面对表征缝网的流动过程进行建模,并分析改造区内人工缝导流能力以及天然裂缝密度和导流能力对产能的影响.

1 水平井体积压裂缝网表征基本模式

目前,对水平井体积压裂后形成裂缝网络的表征以及渗流模型的建立主要有两类处理方法,即Brown[7],Ozkan[8],Imad[9]等国外学者将改造区内的裂缝网络（各压裂段之间）完全等效为双重孔隙介质,通过耦合线性流模型对其流动过程进行建模；国内学者苏玉亮引入体积压裂带宽的概念对缝网表征方法及渗流模型进行了扩展,认为在段间距较大时,各段之间的部分区域仍未被改造,即段间同时包含了改造区和未改造区[10].以上学者均是将缝网等效为双重孔隙介质,所建立的渗流模型对压裂优化设计和压后产能评价具有一定的指导意义.但当段间距、簇间距较大以及天然裂缝发育程度较低,即缝间距较大时,缝网可能达不到等效为双重孔隙介质的要求[11].虽然文献[12]认为改造区由储层基质、天然裂缝和人工裂缝三重孔隙介质组成,并假设天然缝与所有人工缝正交,但其流动模型未考虑地层流体从基质直接到人工缝的流动,因此,仍需对水平井体积压裂缝网渗流数学模型进行完善.

2 水平井体积压裂渗流的数学模型

假设在一个压裂段内,存在天然缝与人工缝,各段内人工缝条数对应分簇数,天然裂缝等间距分布在人工缝上,并与其正交,相邻段有以下三种基本模式：①压裂段相互独立,各缝网系统不相交,如图1（a）；②压裂段重叠,缝网系统通过天然缝沟通,如图1（b）；③压裂段既重叠又独立,重叠部分通过天然缝沟通,如图1（c）.地层流体从基质向生产井筒流动中,存在基质到天然裂缝、基质到人工裂缝、天然裂缝到人工裂缝和人工裂缝到井筒四个流动过程.前两种为油藏流动,后两者为缝网内部流动.该流动模式与国内外学者[7－10,12]的不同在于：缝网内存在如图2所示的人工缝与天然缝交汇流动.

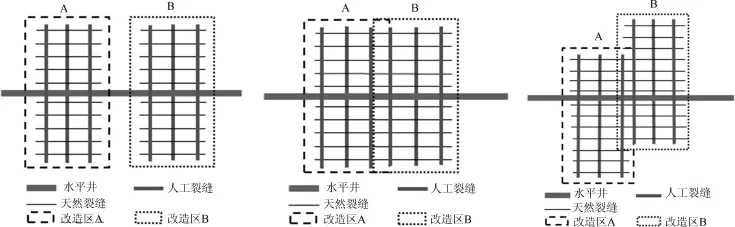
图1 缝网模型表征模式Fig.1 Basic models for fracture network characterization

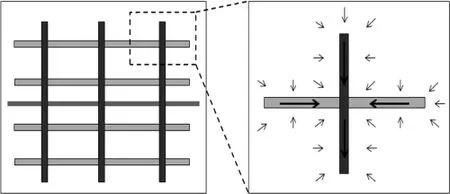
图2 体积压裂缝网内裂缝交汇流动Fig.2 Interplay flow between interconnected fractures in network

压裂基本参数：水平井共进行了MF段压裂,每段有SF簇,段间距为LD,簇间距为LS,每条压裂缝完全穿透储层,人工缝半长为LF,导流能力为kFwF；天然缝与人工缝正交,天然缝长度为Lf,导流能力为kfwf,以密度ρf等间距分布在人工缝上；油层为均质、等厚、上下封闭无界油藏；忽略油藏中流体、基质和裂缝的可压缩性,即地层流体流动为单相稳态渗流.

2.1 裂缝微元划分

首先,将人工缝和天然缝离散为若干微元,各裂缝微元有不同的压力和流量.每条人工裂缝半长等分为NF个长度ΔLF的微元；每条天然裂缝等分为Nf个长度ΔLf的微元,则缝网中共有微元NS个,NS＝MFSFNF＋ρfLFNf（图3）.

其次,将人工裂缝微元从下到上,从左到右依次编号,则第i人工裂缝中的第j微元编号为NF（i－1）＋j,其中,1≤i≤MFSF,1≤j≤NF.同理,将天然裂缝微元从左到右,从下到上依次编号,则第i天然裂缝中的第j微元编号为NFMFSF＋Nf（i－1）＋j,其中,1≤i≤ρfLF,1≤j≤Nf.

2.2 油藏流动方程

由势方程可知,第i裂缝微元在油层M（x,y）点产生的势为[13－14]

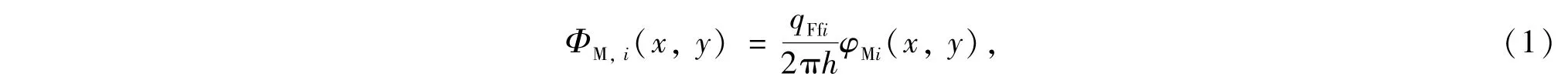
其中,1≤i≤NS,ΦM,i（x,y）为油层中M（x,y）点的势函数,m2·d－1；φMi（x,y）为势函数的几何部分,无因次；qFfi为油层流向裂缝微元的流量,m3·d－1；h为油层厚度,m.式（1）中的几何部分φM,i（x,y）为

图3 体积压裂缝网示意图Fig.3 Schematic of hydraulic fracture network

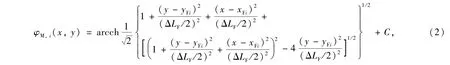
其中,（xFi,yFi）为微元的几何中心坐标,m.

设供给边界处的势为Φe,由叠加原理可得,体积压裂水平井正常生产时在点M（x,y）产生的势为

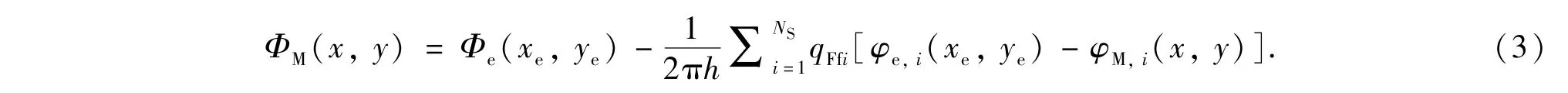
将等式（3）应用于裂缝网络中的全部微元,则每个裂缝微元压力与流量的关系矩阵为

式中,pe为供给边界处的压力,MPa；pFfi为第i裂缝微元的压力,MPa；km为油层渗透率,10－3μm2；μ为地层流体粘度,mPa·s；φi,j和φe,j分别表示第j裂缝微元在第i裂缝微元中心及供给边界处产生势的几何部分.给定裂缝微元压力pFfi,由等式（4）求得油层到裂缝微元的流量qFfi.

2.3 裂缝网络内部流动方程

先不考虑人工缝与天然缝正交所形成的交汇流动,通过组合两种缝的离散控制方程,形成包含人工缝和天然缝的拟缝网流动；再利用星三角变换法对相交的裂缝微元控制方程进行变换,进而修正之前得到的拟缝网流动方程来体现两种缝的交汇流动.

2.3.1 拟缝网流动

人工缝与天然缝内流动为一维稳态渗流.以人工缝为例,其稳态流动表达式为

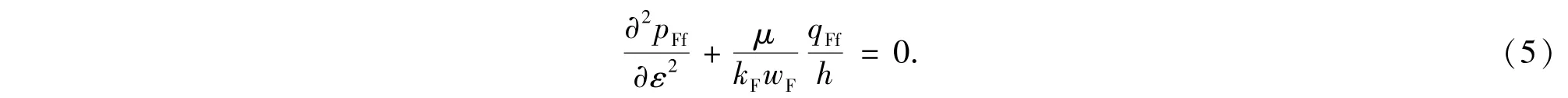
离散等式（5）为有限差分形式,则对于任意裂缝微元,其离散后的控制方程为

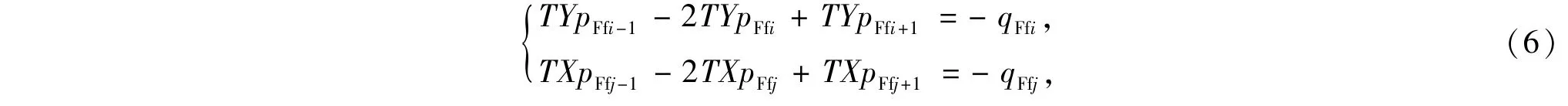
式中,TY＝kFwFh/（μΔLF）,TX＝kfwfh/（μΔLf）；kFwF为人工缝导流能力,μm2·cm；kfwf为天然缝导流能力,μm2·cm；ΔLF为人工裂缝微元长度,m；ΔLf为天然裂缝微元长度,m.

若定井底流压生产,人工缝内边界（与井筒相连部分）则为定压边界,外边界（裂缝端部）为封闭边界.对于天然缝,其两端均为封闭边界.利用等式（6）,并结合裂缝的内外边界条件,可得人工缝及天然缝流动的矩阵形式

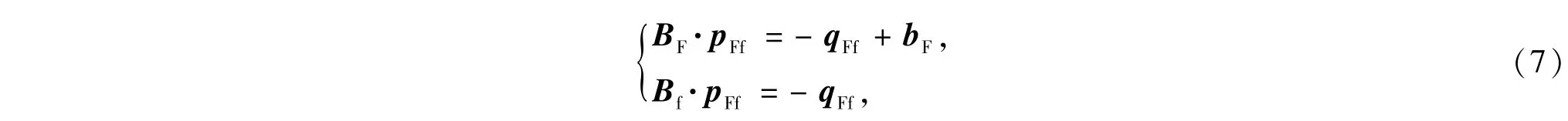
式中,

pw为井底流压,MPa.将包含所有MFSF条人工缝和ρfLF条天然缝,但没有考虑裂缝交汇流动的拟缝网流动方程写成矩阵形式,

2.3.2 人工缝与天然缝交汇流动

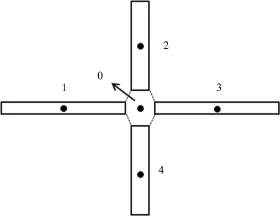
图4 人工裂缝与天然裂缝正交单元Fig.4 Intersection unit between hydraulic and natural fractures

以人工缝与天然缝的某一正交单元为研究对象,示意图如图4.图4中标号1、3表示天然缝微元,标号2、4表示人工缝微元,标号0为交汇单元.由于交汇点导流能力与裂缝微元相近,流动截面积相同,因此各裂缝微元与交汇单元之间的传导率

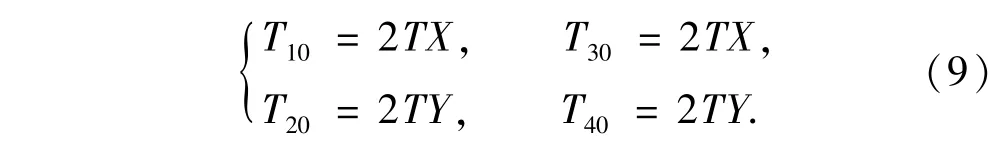
人工缝与天然缝交汇流动时,需知交汇单元0及裂缝微元的压力,才能确定缝网内流体在裂缝微元之间的流动方向及流量分配.但在油藏流动中,交汇单元相对于裂缝微元体积太小,不能作为源项来处理,即不能作为计算点.因此,交汇单元在油藏流动和缝网流动耦合时为奇异点.为消除交汇点,引入星三角变换法来等效处理[5－6]（图5）.经以上变换后,消除了交汇点,使得裂缝微元直接相邻,其相互之间的流体流向及流量大小由裂缝微元的压差和传导率决定.依据星三角变换法,两个裂缝微元间的传导率由下式计算

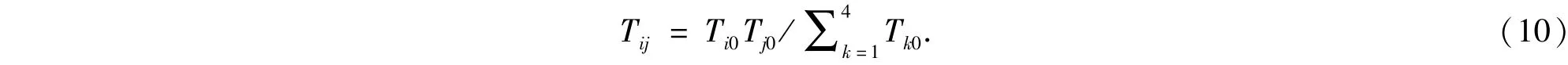
以图4中标号为4的人工缝微元为例,假设与其相邻的另一人工缝微元标号为5.在不考虑人工缝与天然缝交汇流动时,根据等式（6）,其流动方程

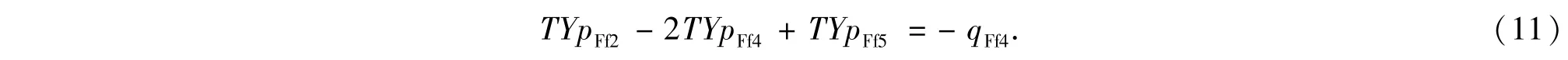
经过星三角变换后,流动方程变为

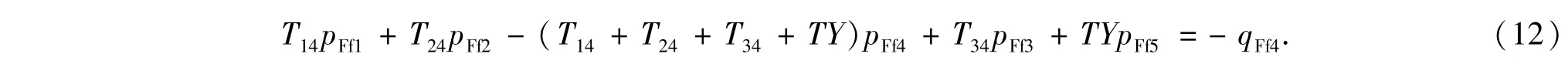
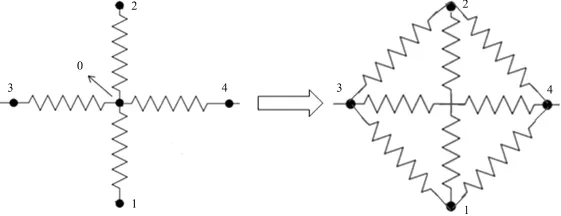
图5 星三角变换法Fig.5 Star-Delta transformation

相对于等式（11）,等式（12）增加的传导率为

对缝网中所有相交的人工缝微元和天然缝微元的控制方程按以上过程变换,即修正等式（8）系数矩阵中对应的行和列元素,便得到考虑裂缝交汇流动的真实缝网内部流动矩阵方程.此方程相对于拟缝网流动,只是等式左端的系数矩阵稍作了变化.为方便以下流动耦合,记修正后的等式（8）左端系数矩阵为CNS×NS,右端常数列向量为DNS×1.

2.4 油藏与缝网耦合流动

油藏流动中,要得到油层流向裂缝微元的流量qFf,必须已知裂缝微元的压力pFf；而在缝网内部流动中,要求解裂缝微元的压力,则须已知油层流向裂缝微元的流量.该两个流动方程的求解是相互耦合的过程.利用油藏流动等式（4）和经星三角变换法修正后的缝网内部流动等式（8）,消去qFf,得计算pFf等式

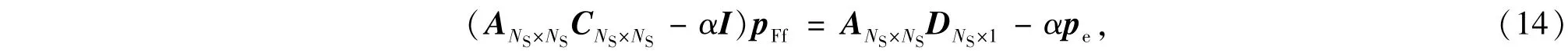
其中,I为NS×NS单位矩阵.将求解的pFf代回等式（4）,便求得qFf,进而得到缝网中每条裂缝的产量和体积压裂水平井总产量.

3 产能影响因素

在水平井长度一定的情况下,压裂段数、人工缝半长与人工缝导流能力及天然缝分布密度与天然缝导流能力都是影响水平井初期产能的重要因素.为分析以上参数对产能的影响规律,设基本参数为：油藏厚度40 m,油藏渗透率0.2×10－3μm2,流体黏度1.02 mPa·s,生产压差5 MPa,水平井改造段长度900 m.

3.1 压裂段数及段内分簇数对产能的影响

假设人工缝半长250m,人工缝导流能力50μm2·cm,天然缝密度70条/100m,天然缝导流能力5μm2·cm.各压裂段以及段内各簇均等间距分布在水平井改造段上.计算不同压裂段数及段内分簇数下的产能曲线.

从图6可以看出：压裂段数对产量影响较大,产量最大相差一倍多；随压裂段数的增加,人工缝与天然缝形成的裂缝网络变大,产量增加,但后期增幅减小,最佳压裂段数范围在10～12之间.如图7所示,段内分簇数对产量的影响规律与压裂段数相似,但影响程度较小,最大相差6.2 m3·d－1.

3.2 人工裂缝半长及导流能力对产能的影响

设水平井分10段压裂,段间距96 m,每段分3簇,簇间距10 m；天然缝密度70条/100 m,导流能力5μm2·cm.分析不同人工缝半长与人工缝导流能力对产能的影响,结果见图8.

人工裂缝导流能力对产量的影响主要体现在裂缝半长较大时,随人工缝导流能力的增加,产量逐渐增加,而后增幅变缓.人工缝半长变大,产量变大；裂缝导流能力越高时,裂缝半长的增加对产量的贡献越大.

图6 不同压裂段数下的产能曲线Fig.6 Productivity with different number of stages

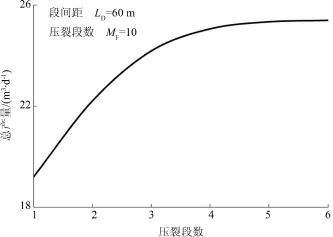
图7 不同段内分簇数下的产能曲线Fig.7 Productivity with different number of clusters

3.3 天然裂缝密度及导流能力对产能的影响

设水平井分10段压裂,段间距96 m,每段分3簇,簇间距10 m；人工裂缝半长250 m,导流能力30μm2· cm.计算天然裂缝密度及导流能力对产能的影响.结果见图9.

图8 不同人工缝半长及导流能力下的产能曲线Fig.8 Productivity with different half-length and conductivity of hydraulic fractures

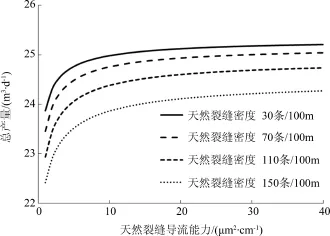
图9 不同天然缝密度及导流能力下的产量曲线Fig.9 Productivity with different density and conductivity of natural fractures

产量与天然缝导流能力并非线性关系,随着天然缝导流能力的增加,产量增幅减缓.天然裂缝密度越大,对产能影响越显著.相比较而言,天然缝密度对产能的影响要比天然缝导流能力的影响更显著；而天然缝对产量的影响要远小于人工缝的影响.因此,水平井改造段长度一定时,压裂段数与段内分簇数是决定产能的最主要因素,其次是人工裂缝半长和人工缝导流能力,天然裂缝密度和导流能力对产量影响较小.

4 实例应用

以我国长庆油田分段多簇压裂水平井W1井为例,采用缝网定量表征方法量化其改造体积,并利用耦合模型计算其生产指标.W1井设计压裂8段,每段分4～5簇进行射孔.现场实施中,第1段未成功压裂,有效压裂为第2～8段.其中,段间距LD为32 m,簇间距LS为11 m；第2、3、4、8段分4簇,第5、6、7段分5簇.微地震事件及估计压裂体积如图10（a）所示.其中,第2段压裂与第3段重叠并与其它段独立,对应图1（a）模式；第4～8压裂段相互重叠,利用天然缝沟通,但各段也有独立部分,是图1（b）和图1（c）模式的结合.通过三种模式的不同组合,将该改造区表征为两大缝网系统,同时将人工缝与天然缝显式地表示,表征结果见图10（b）.该井所处地层物性、压力系统及流体基本参数见表1.微地震监测结果以及定量化指标如表2.

图10 体积压裂水平井缝网表征示意图Fig.10 Schematic of fracture network characterization for horizontalwellW1

电成像测井分析储层天然裂缝平均密度为40条/100 m,且其走向与人工缝走向垂直.人工缝和天然缝的导流能力分别为20μm2·cm、4μm2·cm.该井在压后生产前4个月产液量稳定,平均28.92 m3·d－1.利用耦合流动模型计算得,理论稳定产量为25.47 m3·d－1,与实际值相差仅9％,吻合程度较高.如图11所示,压裂段的产量分布规律呈端部高,内部低的趋势,反映了由于每段改造情况的不同而形成的产量差异.如第3段和第4段改造情况较差,产量较低；虽然第5段压裂效果稍差于第6段,但由于第3、4段改造差所造成的产能损失使附近地层向第5压裂段供液增强,产量变大.对于两大改造区的产量,改造区②的产量（16.33 m3· d－1）较改造区①的产量高（9.14 m3·d－1）.

表1 地层及流体计算参数Table 1 Parameters of formation and reservoir fluid

表2 微地震监测及定量化结果Table 2 Results ofm icroseism ic im age and fracture characterization

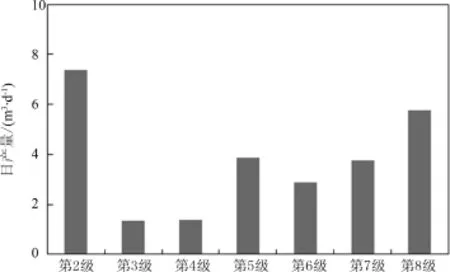
图11 段产量分布Fig.11 Productivity distribution of fracture segment

5 结论

1）针对岩石脆性系数高且天然裂缝发育的低渗透储层,提出了定量表征水平井体积压裂缝网的三种基本模式.

2）建立了水平井体积压裂缝网流动数学模型,并提出了相应的矩阵耦合求解方法.

3）以表征的缝网为基础,利用耦合流动模型预测了体积压裂水平井初期产能,理论计算值与实测值吻合较好.

4）水平井改造段长度一定时,压裂段数与段内分簇数是决定产能的最主要因素,其次是人工裂缝半长和人工缝导流能力,天然裂缝密度和导流能力对产量影响较小.

[1] Lei Qun,Xu Yun,Jiang Tingxue,etal.“Fracture network”fracturing technique for improving post-fracturing performance of low and ultra-low permeability reservoirs[J].Acta Petrolei Sinica,2009,30（2）：237－241.

[2] Wu Qi,Xu Yun,Liu Yuzhang,etal.The current situation of stimulated reservoir volume for shale in U.S.and its inspiration to China[J].Oil Drilling＆Production technology,2011,33（2）：1－7.

[3] Weng Dingwei,Lei Qun,Xu Yun,et al.Network fracturing techniques and its application in the field[J].Acta Petrolei Sinica,2011,32（2）：280－284.

[4] Wu Qi,Xu Yun,Wang Xiaoquan,etal.Volume fracturing technology of unconventional reservoirs：Connotation,optimization design and implementation[J].Petroleum Exploration and Development,2012,39（2）：352－355.

[5] King PR.The use of renormalization for calculating effective permeability[J].Transport in Porous Media,1999,4（1）：37－58.

[6] Karimi-Fard M,Durlofsky L J,Aziz K.An efficient discrete fracturemodel applicable for general purpose reservoir simulators [R].SPE 79699-MS,2003.

[7] Brown M,Ozkan E,Raghavan R,et al.Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs[R].SPE 125043-MS,2009.

[8] Ozkan E,Brown M,Raghavan R,etal.Comparison of fractured horizontalwell performance in tight sand and shale reservoirs [J].SPE Reservoir Evaluation＆Engineering,2011,14（2）：248－259.

[9] Imad B,Mehran PD,Roberto A.Modeling fractured horizontalwells as dual porosity composite reservoirs-application to tight gas,shale gas and tight oil cases[R].SPE 144057-MS,2011.

[10] Su Yuliang,WangWendong,Sheng Guanglong,et al.Compound flow model of volume fractured horizontal well[J].Acta Petrolei Sinica,2014,35（3）：504－510.

[11] Mayerhofer M J,Lolon E P,Youngblood J E,et al.Integration of microseismic fracture mapping results with numerical fracture network production modeling in the barnett shale[R].SPE 102103-MS,2006.

[12] Al-Ahmadi H A,Almarzooq A M,Wattenbarger R A.Application of linear flow analysis to shale gas wells-field cases[R].SPE 130370-MS,2010.

[13] Lang Zhaoxin,Zhang Lihua,Cheng Linsong.Investigation of productivity of fractured horizontal well[J].Journal of University of Petroleum,China（Edition of Natural Science）,1994,18（2）：43－46.

[14] Cheng Linsong,Pi Jian,Lian Peiqing,et al.A computationalmethod of productivity of horizontal well in naturally fractured reservoirs[J].Chinese JComput Phys,2011,28（2）：230－236.

Characterization of Fracture Network by Volume Fracturing in HorizontalW ells and Coupled Flow M odel

JIA Pin1, CHENG Linsong1, HUANG Shijun1, TIAN Xiaofeng2
（1.Faculty of Petroleum Engineering,China University ofPetroleum（Beijing）,Beijing 102249,China；
2.CNOOCResearch Institute,Beijing 100027,China）

For reservoirs with high rock brittleness coefficient and uniform development of natural fractures,three basic modes are developed to characterize fracture network created by volume fracturing in horizontalwells.Flow from reservoir towellbore is divided to two parts：reservoir flow and network flow.Principle of potential superposition is used to derive reservoir flow equation.Finitedifferencemethod is adopted to establish flow equation within finite conductivity network.Star-Delta transformation is used to tackle interplay of flow between hydraulic and natural fractures.A comprehensive flow model is presented by couplingmatrix equations of two flows.It indicates that as stimulated horizontal length is kept constant,effect of quantity of fracture stages and perforation clusters in each stage on production ismore significant than thatof half-length and flow conductivity of hydraulic fracture,which is,in turn,more dominant than that of density and flow conductivity of natural fractures.Finally,a field example shows that little difference exists betweenmeasured and calculated results.

volume fractured horizontal well；fracture network；quantitative characterization；Star-Delta transformation；coupled flow；productivity

1001-246X（2015）06-0685-08

TE312

A

2014－10－13；

2015－02－22

国家自然科学基金（51174215）资助项目

贾品（1990－）,男,博士生,从事油藏工程和渗流理论研究,E-mail：jiapin1990＠163.com