基于LM算法的相对测量相机非线性标定技术

田少雄，卢 山，刘宗明，孙 玥，刘付成，曹姝清

（1.上海航天控制技术研究所，上海 201109；2.上海市空间智能控制技术重点实验室，上海 201109）

0 引言

基于光学成像的视觉相对导航系统因其体积小、重量轻、寿命长和可靠性高等优点，已成为空间任务中获得航天器间相对位姿信息的重要手段［1］。计算机视觉系统用相机从空间获取图像信息，如欲通过三维重建得到空间物体的位置、姿态等信息，须知道三维空间点与图像像素间的对应关系，这就需要对相机进行标定。相机标定技术主要分为传统标定方法和自标定方法两类。自标定方法又称为弱标定，精度不高，鲁棒性不强［2－3］。传统的标定方法又分为线性标定和非线性标定两类。相机线性标定不考虑相机镜头的畸变，算法速度快，但精度较低，且对噪声敏感，适用一般场合［4］。相机非线性标定引入了相机的畸变参数，模型更精确，标定精度较高。在非线性模型中，虽然引入相机畸变因素可补偿镜头畸变的影响，但算法的迭代需选取良好的初值，且模型越精确，计算代价越高。文献［5］基于径向约束（RAC）的两步法标定，可保证较高的精度，但需对图像中心等参数进行预标定。文献［6］引入一阶径向畸变，用非线性迭代法优化摄像机相关参数，一定程度提高了标定精度。文献［7］采用基于神经网络的标定方法，可求解复杂的非线性问题，但训练网络需要有足够的样本，且泛化能力差。

Levenberg－Marquardt算法是一种性能优良的最优化算法，结合了梯度法和牛顿法的优点，且收敛性强。为此，本文对一种基于 Levenberg－Mar－quardt算法的相机非线性标定方法进行了研究。

1 相机非线性模型

相机的针孔模型又称为线性相机模型［8］。空间中任意一点P在图像中的投影点p可用针孔模型近似表示，如图1所示。

图1 相机模型Fig.1 Camera model

设（u，v）为投影点p的图像像素坐标；（Xc，Yc，Zc）为空间点P在相机坐标系中的坐标，两者关系可用齐次坐标表示为

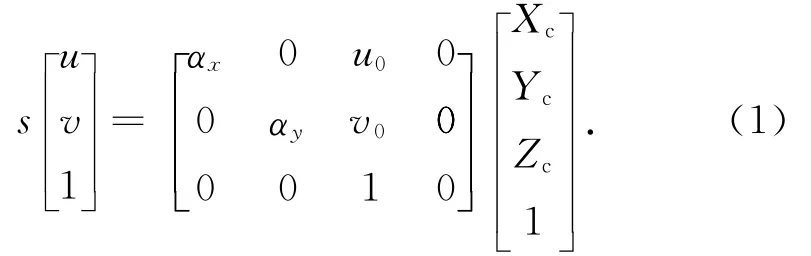
式中：s为比例因子；αx，αy分别为u、v轴上的尺度因子；（u0，v0）为像面主点位置。

设（Xw，Yw，Zw）为空间点P在世界坐标系中的坐标，点P在世界坐标系和相机坐标系中的关系可用齐次坐标表示为

式中：R为相机坐标系的旋转矩阵；t为世界坐标系和平移向量。

由式（1）、（2）可得，世界坐标系表示的空间点P与其投影点p坐标的关系为

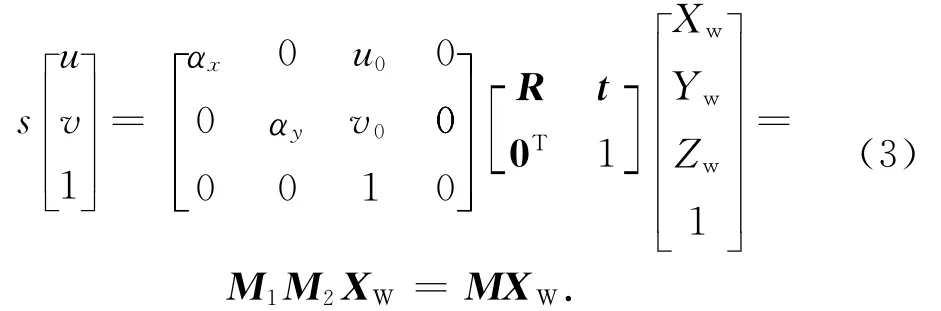
式中：M1为线性相机内部参数，取决于αx，αy，u0，v0；M2为相机外部参数，取决于相机坐标系相对世界坐标系的方位。

实际工程中，由于镜头的弯曲和安装误差等影响，镜头并非理想的透镜成像，而带有不同程度的畸变，使空间点所成的像不在线性模型描述的位置，而是在受到镜头失真后影响有一定偏移［9］。

在针孔模型中对Pc（Xc，Yc，Zc）作归一化投影，可得归一化的图像坐标为

式中：（x，y）为理想图像坐标值。

令（xd，yd）为在受镜头失真后影响而偏移的实际像平面坐标，且

式中：δx，δy为线性畸变值。畸变模型一般包括径向畸变和切向畸变。

a）径向畸变

径向畸变主要来自镜头形状，光学中心的径向畸变为0，随着向边缘移动，径向畸变越来越严重，其数学模型为

式中：r2＝x2＋y2；k1，k2，…为径向畸变系数。

b）切向畸变

切向畸变主要是由透镜制造中的缺陷使透镜本身与图像平面不平行产生的，其数学模型为

式中：p1，p2，…为切向畸变系数。

为保证精度和迭代速度，本文仅考虑径向畸变和切向畸变的前两项，这已能获得足够的精度，则（xd，yd），（x，y）满足关系

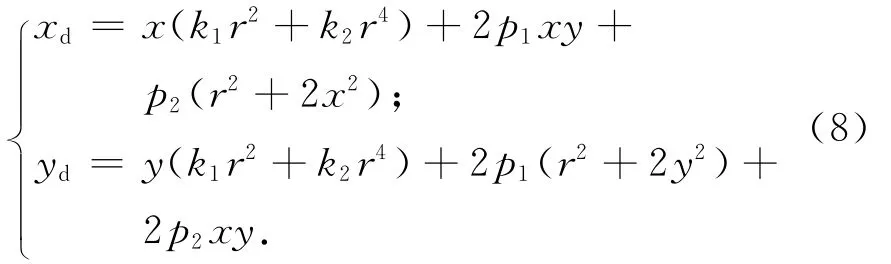
将归一化的实际图像坐标转换为在图像像素坐标系的坐标，由式（1）有

上述线性模型的参数αx，αy，u0，v0与非线性畸变参数k1，k2，p1，p2构成了非线性模型的相机内部参数。

2 初值求解

本文用直接线性变换法（DLT）计算相机内外参数的初值，通过求解线性方程可求得相机模型的参数。

由式（3）可得

式中：（Xwi，Ywi，Zwi，1）为3D 立体靶标第i个点的坐标；（ui，vi，1）为第i个点的图像坐标。式（10）消去si后可得两个关于mij的线性方程

对n个特征点，可得2n个关于M阵元素的线性方程。实际上，M阵乘以任意不为零的常数不会影响（Xw，Yw，Zw）与（u，v）间的关系，故可指定m34＝1，当2n＞11时，可用最小二乘法可求出M阵的所有元素。求出M后，可分解获得相机的线性内外参数。

3 Levenberg－Marquardt非线性优化

由直接线性变换法求得相机线性模型的内外参数初值后，对其进行非线性优化。对于n个标定点，可通过最小化目标函数

对内外参数进行优化。此处：（xdi，ydi），（ui，vi）分别为第i个点的模型和实际坐标。

本文用LM算法求解最优化问题，LM算法是求解非线性最优化问题的典型算法，结合了最速下降法和 Gauss－Newton法的优点［10］。

设xk为当前解，对式（12），Gauss－Newton法求解问题的试探步为）

式中：J（xk）为Jocobian矩阵。Gauss－Newton法要求Jocobian矩阵为行满秩，故无法用其求解非线性方程组奇异问题。

LM算法对Gauss－Newton法进行改进，将一个正定矩阵ukI加到（J（xk））TJ（xk）上，使之成为正定矩阵，LM算法步长

式中：I为单位矩阵；u为LM参数，当时u→0时，趋于Gauss－Newton法，当u→ ∞ 时，dk趋于最速下降法。

将直接线性变换求得的内外参数作为初值，取k1，k2，p1，p2初值为0，进行迭代计算，算法步骤为

a）输入初值x0，初始参数u＝0.01，设定精度ε＝1×10－7；

b）计算F（x），J（x）；

c）计算dk，则xk＋1＝xk＋dk；

d）若F（xk＋1）＜F（xk），且 ‖dk‖ ＜ε，停止迭代，输出结果；否则，令u＝u／10，转至步骤b）；

e）若F（xk＋1）≥F（xk），令u＝10u，重新计算dk，返回到步骤d）。

4 实验结果

实验相机分辨率2 048pixel×2 048pixel，镜头焦距f＝10mm，像元尺寸5.5μm×5.5μm。以精密三维坐标机为标定靶标，三维坐标机前后移动3个面，共采集世界坐标采样点196个。对采集的靶标点进行图像处理后，可得对应的图像像素坐标。由此获得世界坐标和图像坐标点对196组。

实验中，用直接线性变换法求出相机内外参数的初值，取k1，k2，p1，p2初值为0，用LM 法迭代计算精确解，结果见表1。

迭代优化完成后，分别用初始的内外参数和优化后的内外参数重新投影，计算实测图像坐标与由模型得到的图像坐标的像点坐标误差，初始参数重新投影的像点误差如图2所示，LM优化参数重新投影得到的像点误差如图3所示。

定义实测图像坐标（u，v）与根据模型投影的图像坐标（U，V）的距离平均值

表1 标定结果Tab.1 Calibration result

图2 初始参数反投误差Fig.2 Reprojection error of initial parameters

图3 LM优化参数反投误差Fig.3 Reprojection error of LM optimation parameters

用式（15）分别求得初始参数与LM优化参数反投得到的图像坐标与实测坐标的距离平均值分别为0.172 33，0.045 48。

由重新投影后的像点误差图和距离平均值可知：经非线性优化后，反投像点的误差更趋近于零，与实测坐标间的平均距离也减小很多，标定精度有一定提高。

为进一步验证算法有效性，将本文算法与相机标定的经典算法Tsai法进行比较。Tsai标定法标定结果为：k1＝－0.022 61；内参、外参分别为

Tsai法只考虑了一阶径向畸变，本文方法考虑了一阶和二阶的径向、切向畸变。Tsai重新投影的像点误差如图4所示。

图4 Tsai法标定参数反投误差Fig.4 Reprojection error of Tsai method calibration parameters

由式（15），可得Tsai法标定参数反投得到的图像坐标与实测坐标的距离平均值为0.112 99，略大于本文算法得到距离平均值。比较反投误差和距离平均值和距离平均值可知，本文算法精度较高。

5 结束语

在考虑相机径向畸变和切向畸变情况下，本文用立体坐标机获得标定所用特征点数据，由直接线性变换法求出了相机的线性模型内外参数，用LM算法迭代求解出非线性模型的内外参数。与初始标定结果和Tsai法标定结果比较表明：本文算法能有效提高相机标定精度。

［1］ PHILIP N K，ANANTHASAYANAM M R.Relative position and attitude estimation and control schemes for the final phase of an antonomous docing mission of spacecraft［J］.Acta Astronauica，2003，52：511－522.

［2］ FAUGERAS Q，LUONG T，MAYBANK S.Camera self－calibration：theory and experiments［C］／／In Proceeding of the 2nd European Conference on Computer Vision.Santa Margherita Ligure：Computer Vision－ECCV，1992：321－334.

［3］ MAYBANK S，FAUGERAS O.A theory of self－calibration of a moving camera［J］.International Journal of Computer Vision，1992，8（2）：123－151.

［4］ 高宏伟.计算机双目立体视觉［M］.北京：电子工业出版社，2012.

［5］ TSAI R Y.A versatile camera calibration technique for high－accuracy 3Dmachine vision metrology using off－the－shelf TV cameras and lenses［J］.IEEE journal of Robotics and Automation，1987，RA－3（4）：323－344.

［6］ 夏 艳，苏 中，吴细宝.双目视觉测量系统的标定及三维测量［J］.中国图像图形学报，2008，13（7）：1298－1302.

［7］ 秦庆兵.基于神经网络的摄像机畸变校正研究［D］.沈阳：东北大学，2010.

［8］ 张广军.视觉测量［M］.北京：科学出版社，2008.

［9］ 葛宝臻，李晓洁，邱 实.基于共面点直接线性变换的相机畸变校正［J］.中国激光，2010，37（2）：488－494.

［10］ 袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2001.