轴对称动力学问题的无网格自然邻接点Petrov-Galerkin法

第一作者陈莘莘男，博士，副教授，1975年生

轴对称动力学问题的无网格自然邻接点Petrov-Galerkin法

陈莘莘,李庆华,刘永胜

(华东交通大学土木建筑学院，南昌330013)

摘要：基于无网格自然邻接点Petrov-Galerkin法，提出了复杂轴对称动力学问题求解的一条新途径。几何形状和边界条件的轴对称特点，将原来的空间问题转化为平面问题求解。计算时仅仅需要横截面上离散节点的信息，无论积分还是插值都不需要网格。自然邻接点插值构造的试函数具有Kronecker delta函数性质，因此能够直接准确地施加本质边界条件。有限元三节点三角形单元的形函数作为权函数，可以减少域积分中被积函数的阶次，提高计算效率。数值算例结果表明，所提出的方法对求解轴对称动力学问题是行之有效的。

关键词：轴对称；无网格法；动力响应；自然邻接点插值

基金项目：国家自然科学基金资助项目(11002054, 51074076)

收稿日期：2013-11-08修改稿收到日期：2014-02-26

中图分类号:O241; O343文献标志码：A

Meshless natural neighbour Petrov-Galerkin method for axisymmetric dynamic problems

CHENShen-shen,LIQing-hua,LIUYong-sheng(School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China)

Abstract:A novel algorithm for solving complex axisymmetric dynamic problems was put forward on the basis of the meshless natural neighbour Petrov-Galerkin method. Due to axial symmetry of geometry and boundary conditions, an original three-dimensional (3D) problem was reduced into a two-dimensional (2D) problem. Only a set of discrete nodes on a cross section were needed and no meshes were required for either interpolation or integration. The natural neighbour interpolation shape functions had a Kronecker delta property and therefore the essential boundary conditions could be directly imposed. The three-node triangular finite element shape functions were taken as test functions, they reduced the orders of integrands involved in domain integrals and improved the computational efficiency. Numerical examples showed that the proposed method for solving axisymmetric dynamic problems is effective.

Key words:axisymmetric; meshless method; dynamic response; natural neighbour interpolation

作为一种新的数值计算方法，无网格法可以减少或消除网格划分给数值计算带来的困难，尤其在自适应分析、大变形和裂纹扩展等问题中体现出其独特的优越性，具有广阔的应用前景[1-4]。现有的无网格方法中，Atluri等[5]提出的无网格局部Petrov-Galerkin(MLPG)方法允许试函数和权函数选自不同的函数空间，所有积分都在基于节点的局部子域上进行，无需借助背景积分网格，被誉为是一种真正的无网格方法。但是以移动最小二乘近似为理论基础的MLPG方法，形函数不满足Kronecker delta函数性质，难以准确施加本质边界条件。近年来提出的无网格自然邻接点Petrov-Galerkin法[6-8]不仅充分发挥了局部Petrov-Galerkin法的优势，而且采用了自然邻接点插值构造试函数，从而可以直接准确地施加本质边界条件。目前，该方法在很多领域都得到了广泛的应用[9-12]。

在结构分析中常会遇到一些轴对称问题，它们的几何形状、约束条件及作用的荷载都对称于某一固定轴。轴对称问题是弹性空间问题的一个特殊问题，利用轴对称特性，可以将三维空间问题转换为二维问题，从而快速有效地求解。近年来，许多学者[13-15]都致力于无网格法求解复杂轴对称问题的研究，并相继取得了一些进展。本文对无网格自然邻接点Petrov-Galerkin法应用于轴对称动力学问题进行了研究，详细推导了离散方程，并编制了相应的计算程序。最后，通过数值算例验证了本文方法的有效性和合理性。

1轴对称动力学问题的控制方程

在分析轴对称问题时，通常采用圆柱坐标系(r,θ,z)。以z轴为对称轴，所有位移、应变和应力都与θ方向无关，只是r和z的函数。任一点的位移只有两个方向的分量，即沿r方向的径向位移ur和沿z方向的轴向位移uz。轴对称动力学问题的基本方程如下：

(1)平衡方程

(1)

(2)

式中:σr,σθ,σz和τrz表示应力向量分量，br和bz表示体力向量分量，ρ是质量密度，c是阻尼系数。

(2)几何方程

(3)

(3)本构方程

(4)

式中:

(5)

其中:E为弹性模量，v为泊松比。

应力和位移满足如下的边界条件

(6a)

(6b)

和初始条件

(7a)

(7b)

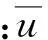
2轴对称动力学问题的离散方程

2.1自然邻接点插值[6-12]

TI={x∈R2:d(x,xI)<

d(x,xJ),∀J≠I}

(8)

式中:d(x,xI)为点x与结点xI的距离。可见，每个TI表示的实际上是以点xI为最近离散节点的空间点位置的集合。在此基础上，进一步可建立计算点x的二阶Voronoi结构，如图1所示。

图1　点x的一阶和二阶Voronoi结构 Fig.1 First-order and second-order Voronoi cells about x

计算点x对节点xI的形函数φI(x)定义为点x与节点xI的Voronoi结构重叠区域的面积AI(x)与点x的Voronoi结构的总面积之比，即

φI(x)=AI(x)/A(x)

(9)

以图1为例，节点1的插值形函数φ1(x)可表示为

φ1(x)=Aabfe/Aabcd

(10)

定义了各节点的插值函数后，点x的位移函数可以写为

(11)

式中:uI(I=1,2,…,n)是点x周围n个自然邻接点的节点位移向量，φI(x)为对应节点的形函数。

2.2控制方程的弱形式及其离散化

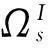
(12)

(13)

式中:vI为加权函数。

对方程(12)的左边项进行分部积分并利用散度定理后，可得

(14)

(15)

图2　局部多边形子域 Fig.2 The local polygonal sub-domains

(16)

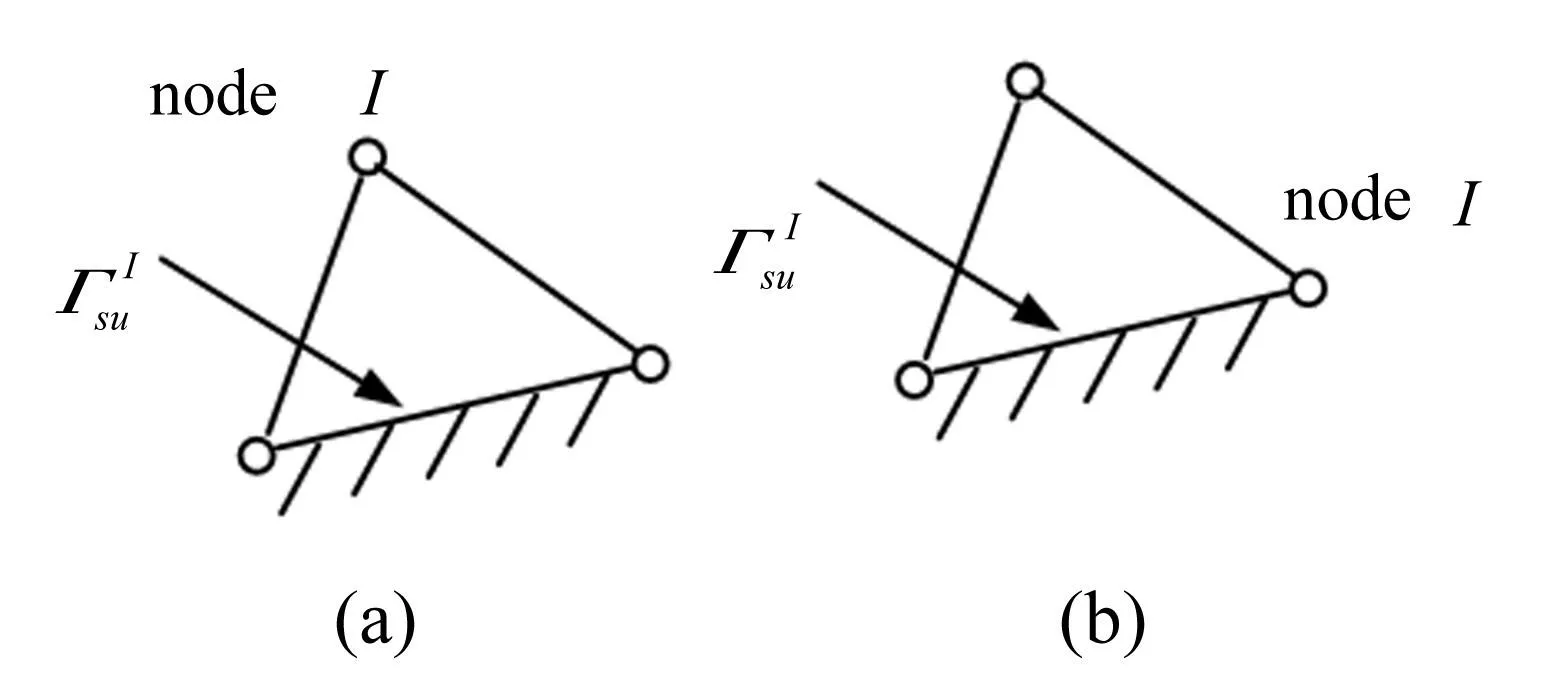
图3　子域Ω I s上的位移边界Γ I su Fig.3 Essential boundary condition Ω I s over sub-domain Γ I su

将式(16)代人式(14),并注意到vI=NI，有

(17)

同理，由方程(13)可得

(18)

联立方程(17)和方程(18)，可得

(19)

式中:

u={ur,uz}T,σ={σr,σθ,σz,τrz}T

(20a)

b={br,bz}T,t={tr,tz}T

(20b)

(20c)

由于只对空间域进行离散，求解域Ω内的试函数u(x,t)可由式(11)表示为

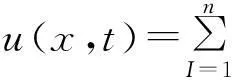
(21)

将空间离散后的位移表达式(21)代入式(19),可得到系统的运动方程如下：

(22)

式中:M,C,K和f(t)分别是系统的质量矩阵、阻尼矩阵、刚度矩阵和节点载荷向量，且它们各元素可具体表示为：

(23a)

(23b)

(23c)

(23d)

其中，

(24a)

(24b)

采用Newmark法对方程(22)进行积分即可以求得系统的动态响应。

图4　受内压的厚壁圆筒 Fig.4 A thick-walled cylinder subjected to internal pressure

3数值算例

3.1受突加载荷的厚壁圆筒

有一无限长厚壁圆筒，其内半径a=0.1 m,外半径b=0.2 m，受突加内压力p=75 MPa的作用，如图4所示。材料的弹性模量E=2.1×1011Pa，泊松比v=0.3，质量密度ρ=7.85×103kg/m3。

计算分析中，截取长L=0.1 m的厚壁圆筒作为计算结构，节点布置方案见图5，且z=0和z=L的节点施加轴向零位移约束。采用时间步长Δt=4.0×10-7s计算得到了不计阻尼情况下内表面的径向位移随时间的变化曲线，如图6所示。为了进行对比，图6还给出了有限元软件ABAQUS(采用6400个CAX4R单元)的计算结果。从图6可以看出，本文的计算结果与ABAQUS的计算结果都吻合很好，从而表明了本文方法的有效性。

图5　厚壁圆筒节点布置 Fig.5 Nodal distribution for a thick-walled cylinder

图6　厚壁圆筒内表面的径向位移 Fig.6 Radial displacement history at the inner surface of the thick-walled cylinder

3.2受突加载荷的厚壁球壳

有一厚壁球壳，其外壁半径R1=0.2 m，内壁半径R2=0.16 m，受突加内压力p=75 MPa的作用。材料参数为E=2.1×1011Pa，v=0.3，ρ=7.85×103kg/m3。

由于对称性，采用如图7所示的节点布置方案。计算时时间步长取为Δt=3.0×10-7s。为了检验方法的有效性，本文采用有限元软件ABAQUS使用12000个CAX4R单元得出的解来对比。图8给出了不计阻尼情况下圆球内壁的径向位移随时间的变化曲线，从图上可以看出本文方法和ABAQUS的结果非常吻合，从而进一步说明了本文方法的有效性。

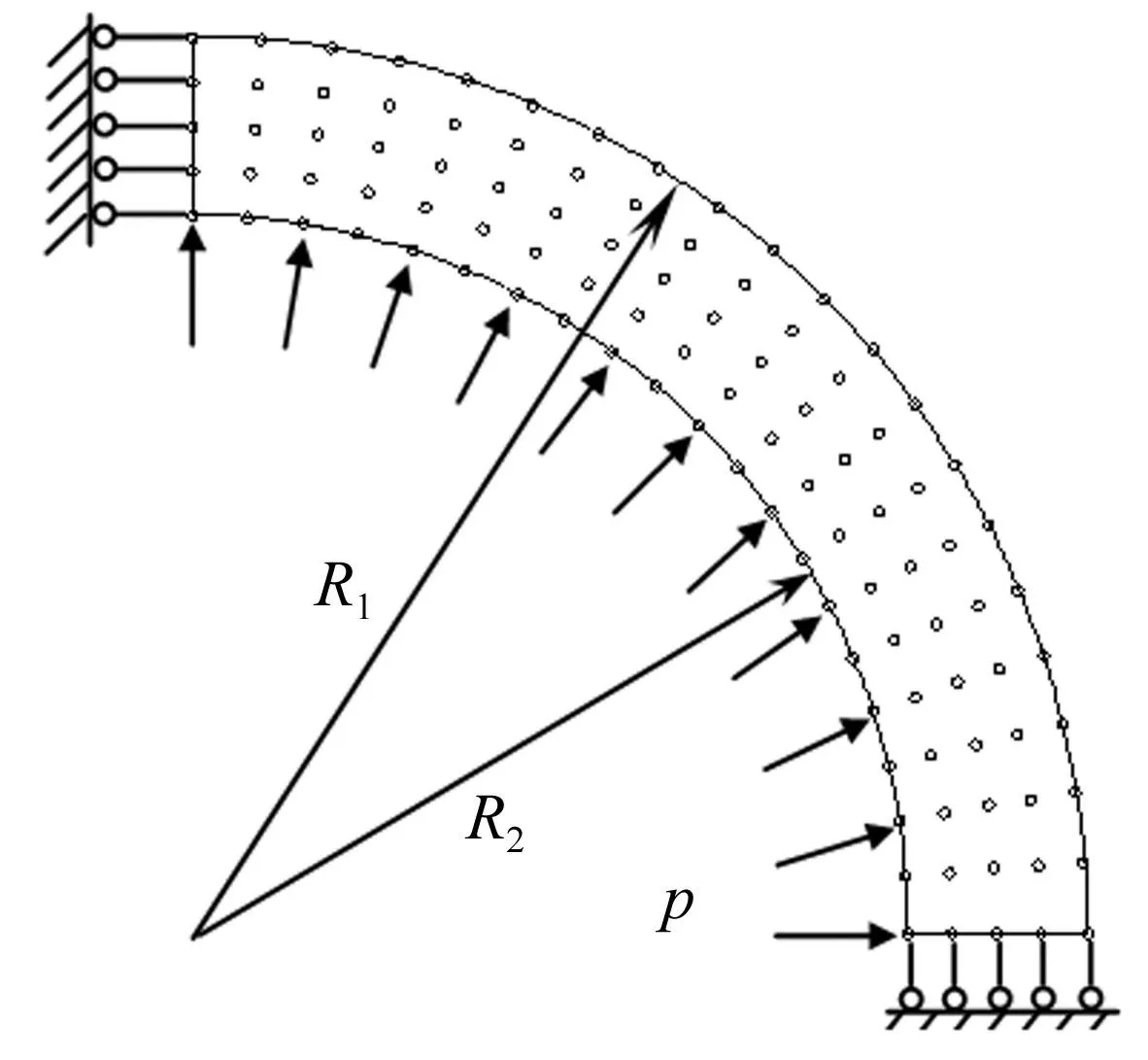
图7　厚壁球壳节点布置 Fig.7 Nodal distribution for a thick-walled spherical shell

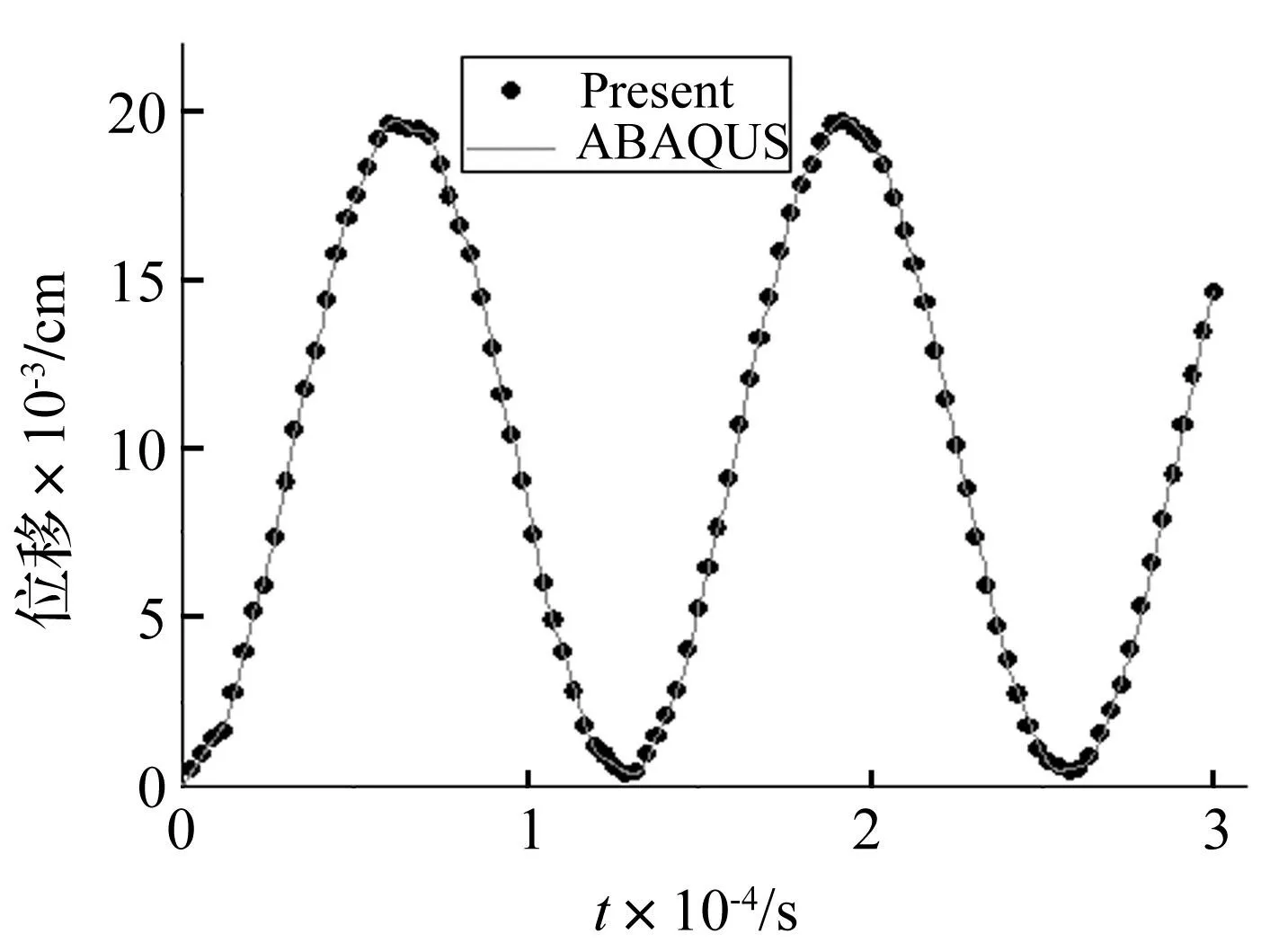
图8　厚壁球壳内表面的径向位移 Fig.8 Radial displacement history at the inner surface of the thick-walled spherical shell

4结论

无网格自然邻接点Petrov-Galerkin法只需要用到模型分布在域内和边界上的节点，并不需要任何单元和网格，因此是一种真正的无网格方法。在求解过程中，采用有限元三节点三角形单元的形函数作为权函数，减少了域积分中被积函数的阶次，提高了计算效率。基于自然邻接点插值构造的试函数，具有Kronecker delta函数性质，从而可以直接准确地施加本质边界条件。

本文借助无网格自然邻接点Petrov-Galerkin法的基本原理，详细推导了轴对称动力学问题的计算公式，并编制了相应的计算程序，最后通过数值算例论证了本文方法的有效性。本文方法还可容易地推广到轴对称裂纹问题的求解计算。

参考文献

[1]Belytschko T, Krongauz Y. Meshless methods: An overview and recent developments [J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(9): 3-47.

[2]刘欣. 无网格方法[M]. 北京：科学出版社，2011.

[3]张雄，刘岩，马上. 无网格法的理论及应用[J]. 力学进展, 2009, 39(1): 1-36.

ZHANG Xiong, LIU Yan, MA Shang. Meshfree methods and their applications [J]. Advances in Mechanics, 2009, 48(5): 1-36.

[4]王峰，林皋，郑保敬，等.基于滑动Kriging插值的无网格MLPG法求解结构动力问题[J]. 振动与冲击, 2014,33(4): 27-31.

WANG Feng, LIN Gao, ZHENG Bao-jing, et al. MLPG method based on moving Kriging interpolation for structural dynamic analysis[J].Journal of Vibration and Shock, 2014,33(4): 27-31.

[5]Atluri S N, Zhu T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics [J]. Computational Mechanics, 1998, 22: 117-127.

[6]蔡永昌，朱合华，王建华. 基于Voronoi结构的无网格局部Petrov-Galerkin方法[J]. 力学学报, 2002, 35(2): 187-193.

CAI Yong-chang, ZHU He-hua, WANG Jian-hua. The meshless local Petrov-Galerkin method based on the Voronoi cells [J]. Acta Mechanica Sinica, 2003, 35(2): 187-193.

[7]Cai Y C, Zhu H H. A meshless local natural neighbour interpolation method for stress analysis of solids [J]. Engineering Analysis with Boundary Elements, 2004, 28: 607-613.

[8]Wang K, Zhou S J, Shan G J. The natural neighbour Petrov-Galerkin method for elasto-statics [J]. International Journal for Numerical Methods in Engineering, 2005, 63: 1126-1145.

[9]李顺利，龙述尧，李光耀. 自然邻接点局部Petrov-Galerkin法求解中厚板弯曲问题[J]. 湖南大学学报, 2011, 38(1): 53-57.

LI Shun-li, LONG Shu-yao, LI Guang-yao. Natural neighbour Petrov-Galerkin method for moderately thick plates [J]. Journal of Hunan University, 2011, 38(1): 53-57.

[10]陈莘莘，刘应华，岑章志. 弹塑性结构安定下限分析的无网格局部Petrov-Galerkin法[J]. 力学学报, 2009, 41(5): 713-721.

CHEN Shen-shen, LIU Ying-hua, CEN Zhang-zhi. A meshless local Petrov-Galerkin method for static shakedown analysis of elasto-plastic structures [J]. Acta Mechanica Sinica, 2009, 41(5): 713-721.

[11]Chen S S, Li Q H, Liu Y H, et al. Dynamic elastoplastic analysis using the meshless local natural neighbour interpolation method [J]. International Journal of Computational Methods, 2011, 8(3): 463-481.

[12]王凯，周慎杰，聂志峰，等. 基于局部自然邻近无网格法的形状优化[J]. 机械工程学报, 2009, 45(10): 185-191.

WANG Kai, ZHOU Shen-jie, NIE Zhi-feng, et al. Shape optimization based on the local natural neighbour Petrov-Galerkin method[J]. Journal of Mechanical Engineering, 2009, 45(10): 185-191.

[13]何沛祥，李子然，吴长春. 轴对称问题中的无网格Galerkin法[J]. 中国科学技术大学学报, 2003, 33(3): 318-323.

HE Pei-xiang,LI Zi-ran, WU Chang-chun. Element free Galerkin method for axisymmetric solids[J]. Journal of University of Science and Technology of China, 2003, 33(3): 318-323.

[14]陈建桥，梁元博，丁亮. 无网格局部Petrov-Galerkin法求解轴对称问题[J]. 华中科技大学学报, 2007, 24(4): 9-12.

CHEN Jian-qiao, LIANG Yuan-bo, DING Liang. Numerical analysis of axisymmetric problems by MLPG [J]. Journal of Huazhong University of Science and Technology, 2007, 24(4): 9-12.

[15]杨建军，郑建龙. 无网格MLPG法求解轴对称弹性力学问题[J]. 工程力学, 2012, 29(8): 8-13.

YANG Jian-jun, ZHENG Jian-long. Analysis of axisymmetric elasticity problems using the meshless local Petrov-Galerkin method [J]. Engineering Mechanics, 2012, 29(8): 8-13.