内爆炸条件下特种圆柱壳结构动力响应研究
第一作者高康华男,博士,1983年生
通信作者王明洋男,博士,教授,1966年生
内爆炸条件下特种圆柱壳结构动力响应研究
高康华1,2,王明洋1,李杰1(1.解放军理工大学爆炸冲击防灾减灾国家重点实验室,南京210007; 2.海军92656部队,海南三亚572000)
摘要:针对有球形顶盖的圆型柱壳结构,基于弹性薄壳振动理论用相同边界梁振型函数近似柱壳振型轴向分布,提出内爆炸荷载作用下此类结构动力响应计算方法,分析长径比对柱壳振动影响,获得结构位移简化算法。通过算例与已有方法对比验证该方法的合理性,并研究顶盖对柱壳振动影响。结果表明,计算径向位移时由柱壳顶端侧向弹性铰支边界考虑顶盖约束,按内部静压条件确定的铰支系数对柱壳振动高阶振型计算时产生误差,在柱壳顶端加入顶盖等效集中质量可有效降低该误差,并使振动频率及顶端径向位移计算值较小;随长径比增大球形顶盖对柱壳振动影响逐渐减小。
关键词:动力响应;计算方法;梁振型函数;圆形柱壳;内爆炸
基金项目:国家自然科学基金青年
收稿日期:2014-03-23修改稿收到日期:2014-05-14
中图分类号:O383文献标志码:A
Dynamic response calculation method for special cylindrical shell structures under internal blast load
GAOKang-hua1,2,WANGMing-yang1,LIJie1(1. State Key Laboratory for Explosion & Impact and Disaster Prevention & Mitigation, PLA University of Science & Technology, Nanjing 210007, China; 2. 92656 Navy Troops, Sanya 572000, China)
Abstract:Based on the classical elastic thin shell theory, cylindrical shell’s modal shape functions were expressed approximately with beam’s modal shape functions under the same boundaries, and the dynamic response calculation methods for cylindrical shells with spherical dome under internal blast load were proposed. The simplified calculation method for the displacement of the shells was obtained by analyzing the influence of slenderness ratio on the cylindrical shells’ vibration. Through calculation examples, the calculated results of the proposed method were compared with those of the existing methods. The rationality of the proposed method was validated, and the influences of dome on the structure vibration were analyzed. The results showed that using the calculation model of cylindrical shell with equivalent concentrated mass of spherical dome, the computing error of shell radial displacements of higher order modes caused by elastic hinge stiffness coefficient obtained under cylindrical shell internal static pressure can be reduced effectively; the calculation results of cylindrical shell modal vibration frequencies and dome radial displacements are smaller than those of the existing methods; the influences of spherical dome on the cylindrical shells’ vibration decrease with increase in the slenderness ratio of the shells.
Key words:dynamic response; calculation method; beam’s modal shape function; cylindrical shell; internal blast
在局部战争及恐怖袭击情况下,核反应堆安全壳、储油罐等组合壳类地面建筑面临爆炸威胁。此类结构主要由底座、筒身及穹顶构成,可视为带球形顶盖的圆形柱壳。对其抗爆研究主要集中于端部带球形封头的圆柱型爆炸容器,常用实验或数值模拟手段分析结构内部压力流场演化[1-2],考虑封头对柱壳端部约束,据应变、位移连续条件确定柱壳两端附加内力[3]。研究重点多集中于容器爆心环面径向位移及环向应变,往往不考虑封头本身质量对柱壳振动影响。而对同类钢筋混凝土组合壳结构内部爆炸的研究则主要以数值模拟为主[4-5]。如内爆炸条件下此类结构动力响应的近似方法[6-7]分别按径向及轴向荷载单独作用时,将柱壳简化为等边界弯曲梁与轴向受力杆计算。本文在此基础上考虑圆形柱壳轴、径向振型耦合,分析球形顶盖对圆柱壳振动影响,研究内爆炸荷载作用下具有球形顶盖圆柱壳结构动力响应计算方法。
1圆形柱壳动力响应计算
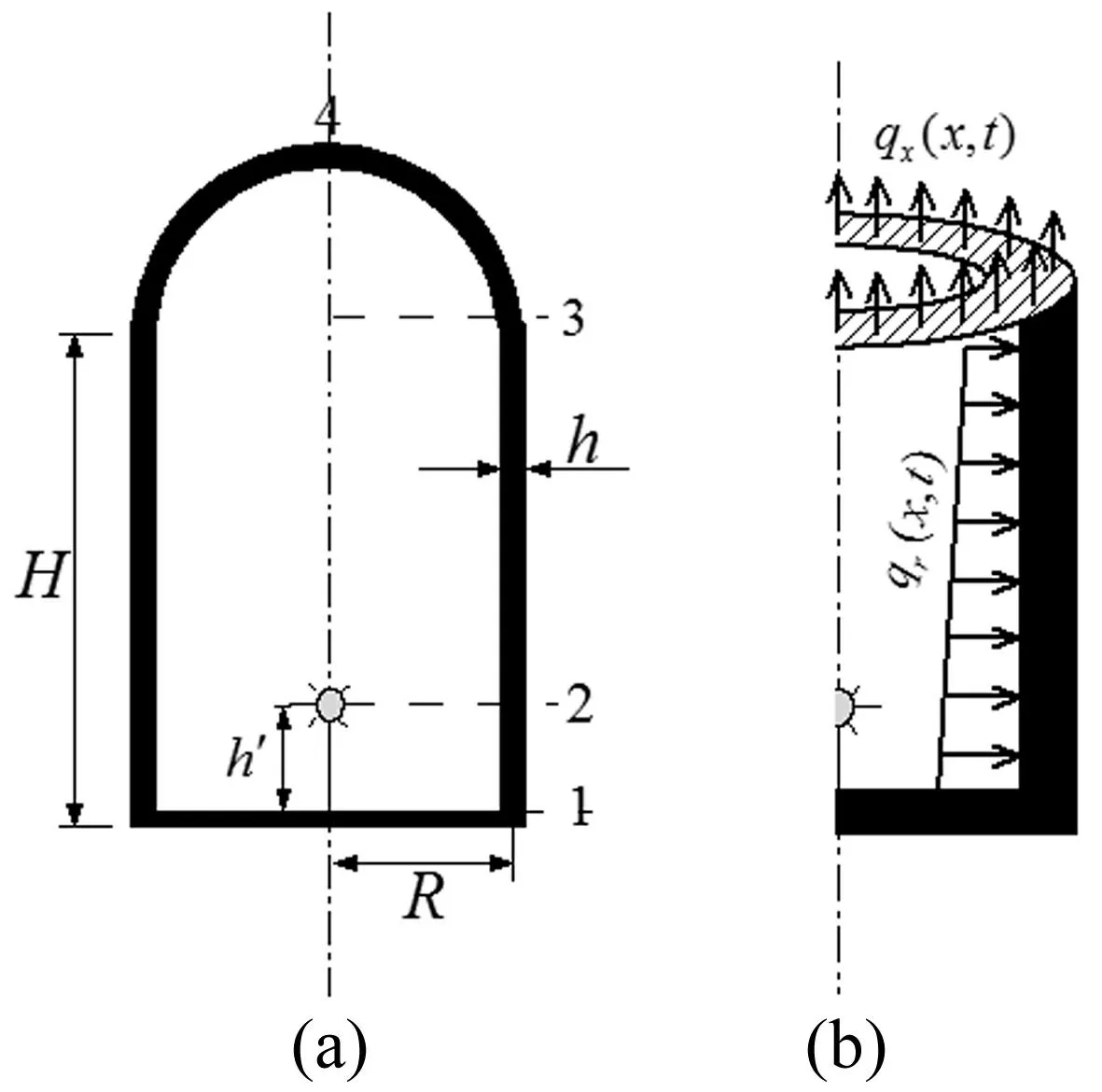
图1 带圆球顶盖圆柱壳内爆炸示意图 Fig.1 Diagram of cylindrical shells structure with spherical dome under internal blast load
带球形顶盖圆柱壳结构示意图见图1(a)。其中h为柱壳与顶盖厚度,H为柱壳高度,R为半径,h′为装药离地面高度。爆源位于结构中轴线,壳体材料视为正交各向异性。顶盖与柱壳连接处往往同时产生薄膜应力及局部弯曲应力,并沿圆周形成均匀分布的剪力、弯矩。当柱壳与球形顶盖厚度相同时剪力使连接处两部分边缘产生相等旋转,此时可认为弯矩为零[8],并通过将柱壳顶部视为弹性铰支边界等效连接处剪力。因顶盖受内部爆炸压力向上运动在柱壳顶端产生纵向拉力,为考虑顶盖惯性运动影响,计算时将顶盖作为集中质量加在柱壳顶部,并假设柱壳同时受径向荷载qr(x,t)与轴向荷载qx(x,t)作用,见图1(b),柱壳变形视为轴对称问题。
据弹性薄壳理论,内爆炸荷载作用下柱壳结构振动方程计算式[9]为
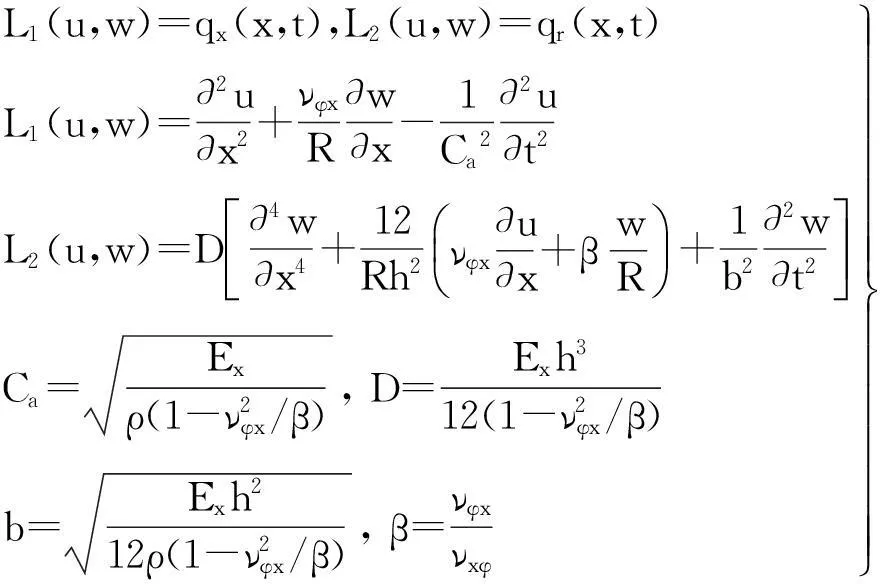
式中:u,w为壳体轴向、径向位移;Ca为正交各向异性材料中纵波波速;D为柱壳弯曲刚度; Ex为x方向弹性模量;vxφ,vφx为x,φ方向泊松比;ρ为壳体材料密度。
1.1内爆炸荷载确定
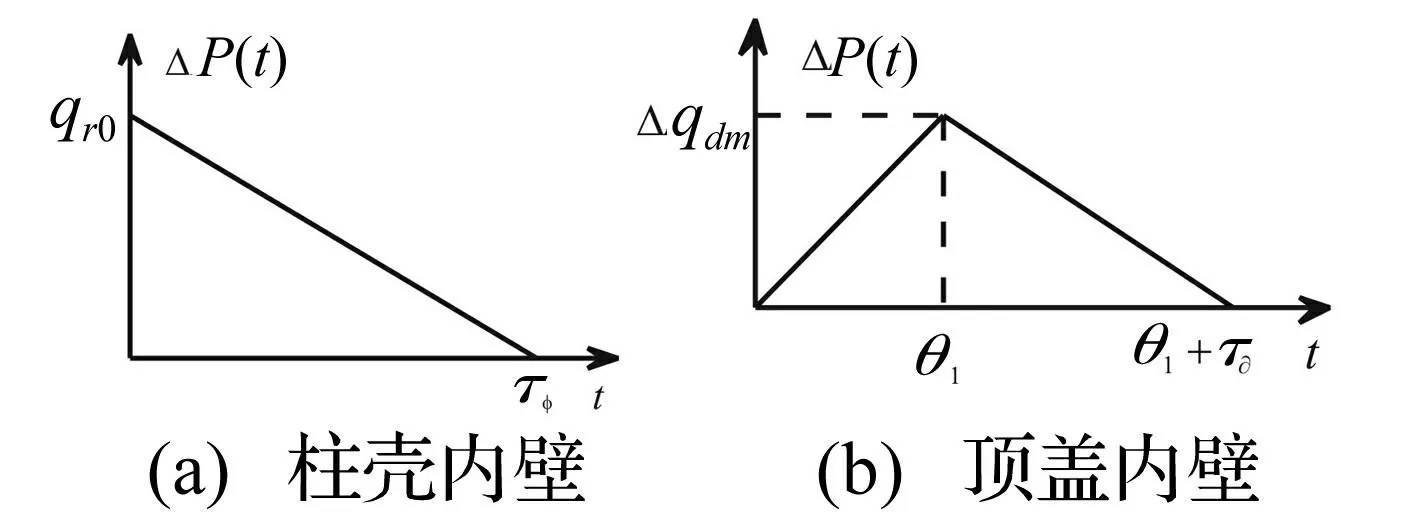
图2 结构内壁某点压力时程图 Fig.2 Load time-history graph of structure inner wall
柱壳内壁荷载可视为沿壳体高度线性分布(图1(b)),内壁某点压力时程见图2(a)。
qr(x,t)=qr0φ(x)f(t)=
(2)
式中:ΔPr1.max,ΔPr3.max分别为点1、3处冲击波峰值反射超压,计算式[10]为
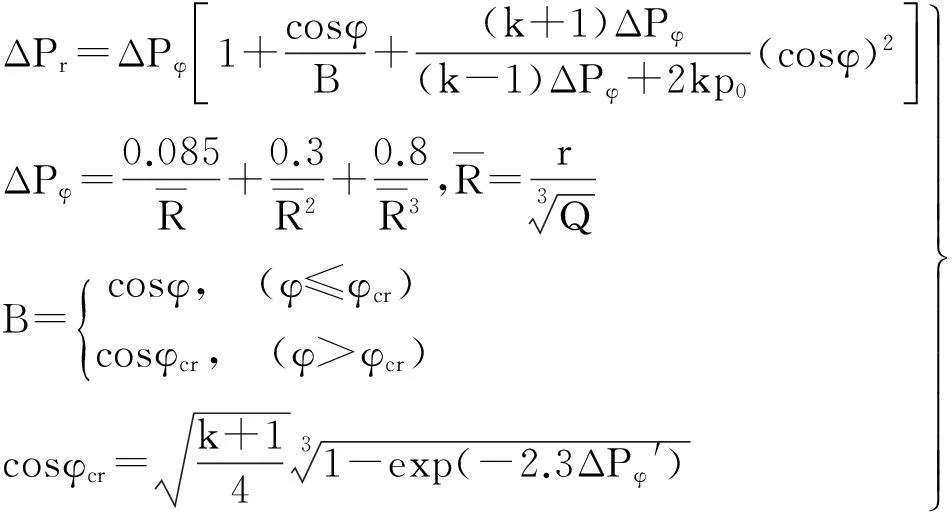
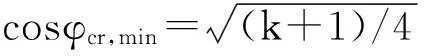
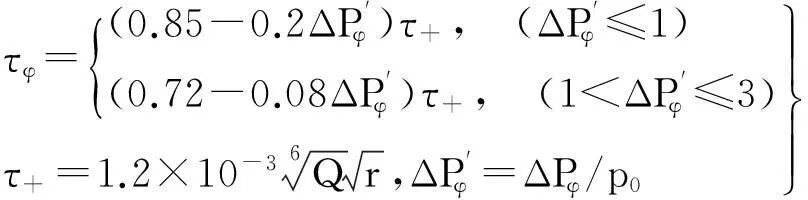
式中:τ+为柱壳内壁压力正相作用时间;τφ为等冲量时正相有效作用时间。
对球形顶盖内壁荷载,假设顶盖各点同时均匀受载,顶盖平均荷载计算见图2(b)。图中ΔPdm为顶盖承受的平均荷载最大值,θ1为顶盖内壁峰值上升时间,θ1+τ∂为荷载正相作用等效时间。将顶盖承受爆炸压力换算至柱壳周边单位长度,则柱壳顶部纵向力qx(x,t)计算式为
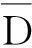
由于柱壳承受径向与轴向荷载形式不同,计算时应据τφ,θ1,θ1+τ∂大小将荷载分段,将每段荷载结束后壳体振动位移及速度作为下段荷载作用的初始条件依次计算。
1.2柱壳动力响应计算
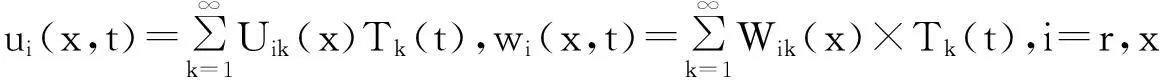
Tk(t)=akcos(ωkt)+bksin(ωkt)+
(6)
式中:ωk为柱壳固有频率;ak,bk由初始条件确定;Pk,Mk分别为广义力及广义质量。
振型Uk(x),Wk(x)计算式[9]为
(7)
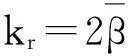
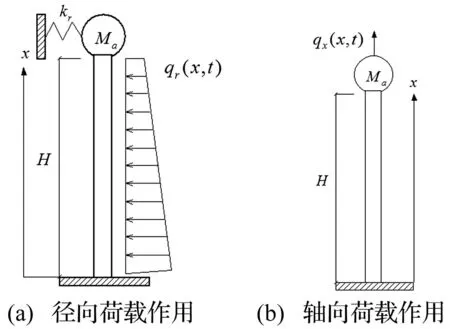
图3 柱壳结构振型计算简图 Fig.3 The vibration mode calculation diagram of cylindrical shell
用梁函数组合法分析径向荷载作用下柱壳结构振动时按弯曲梁假设振型函数(图3(a))。
(8)
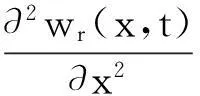
(9)
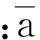
将式(8)、式(9)代入式(7),可得系数Ark,Crk满足的线性方程组;由Ark,Crk存在非零解令其系数行列式为零可得柱壳频率方程。对应每个k解得两个频率值,分别对应两方向位移振型间不同比值,某方向振动位移解均为考虑此两种频率振动叠加,将所得频率值及相应振型系数Ark,Crk代入式(8)即可得壳体振动振型解;联立式(6) 可得柱壳振动位移解。考虑球顶盖等效集中质量,据柱壳正交性,式(6)中Pk(x,t),Mk计算式为
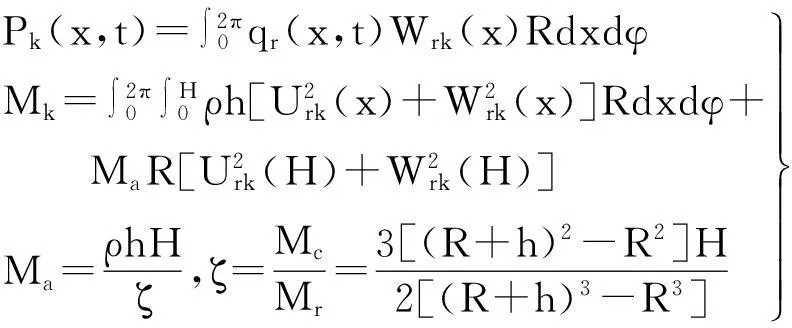
(10)
式中:Mc,Mr分别为壳体、顶盖质量。
端部仅承受轴向拉力的圆柱壳可按顶端带集中质量杆的假设振型函数[6-7](图3(b))。
(11)
ξktanξk=ζ
(12)
对给定ζ可求出ξk,即得系统自振频率。将Uxk(x)=Axksin(ξkx/H),Wxk(x)=Cxkcos(ξkx/H) 代入式(7)并联立式(6)可确定轴向荷载作用下位移ux,wx。考虑带集中质量杆纵向振动振型正交性及壳体顶端纵向受力,Mk(t),Pk(t)应化为
(13)
2简化计算方法
2.1振动频率分析
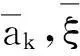
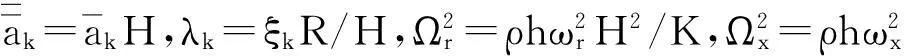
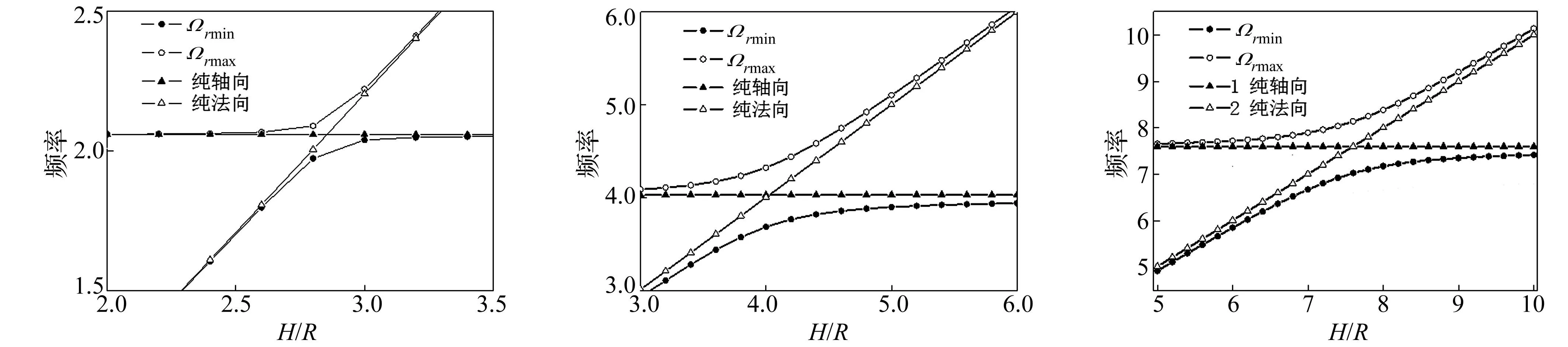
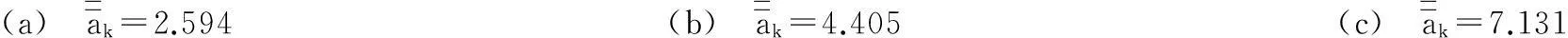
(a) ak=2.594(b) ak=4.405(c) ak=7.131
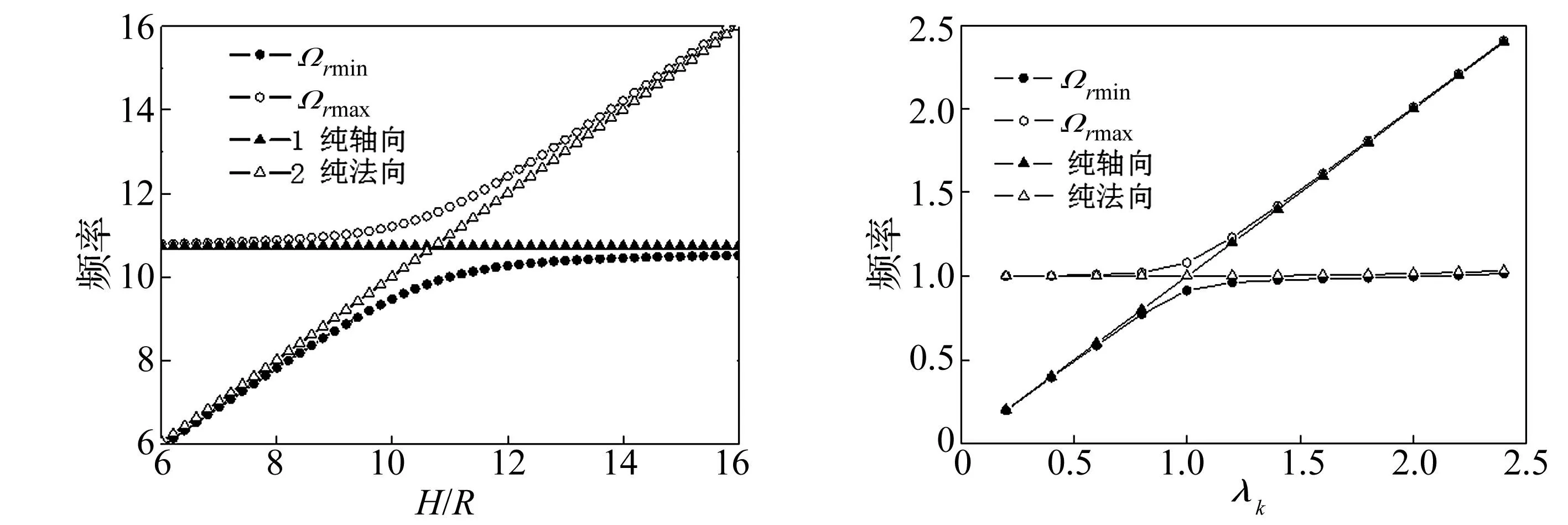

(d) ak=10.253(e) λk~Ωx图4 柱壳自由振动频率计算图Fig.4Graphofcylindricalshellfreevibrationfrequency
2.2柱壳振动的简化解
(14)
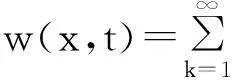
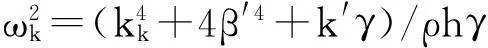
柱壳顶部轴向荷载单独作用时忽略径向振型影响,按(图3(b))单位宽度杆确定振动方程,即
(16)
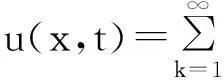
式中:ωk由频率方程(12)确定;对(式(5))分段荷载,Uk(t)计算式为
Uk(t)=
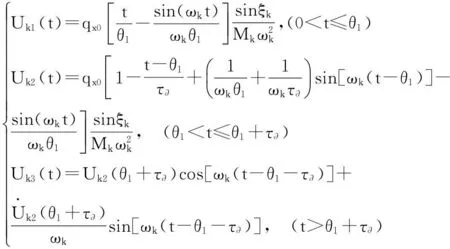
3算例分析
文献[6]的内爆炸条件下具有圆顶盖柱壳结构动力响应近似计算方法,不考虑径向、轴向振动相互影响,按第一振型解确定壳体位移。通过算例将本文方法与文献[6]方法进行对比,壳体材料视为各向同性,具体计算参数见表1。
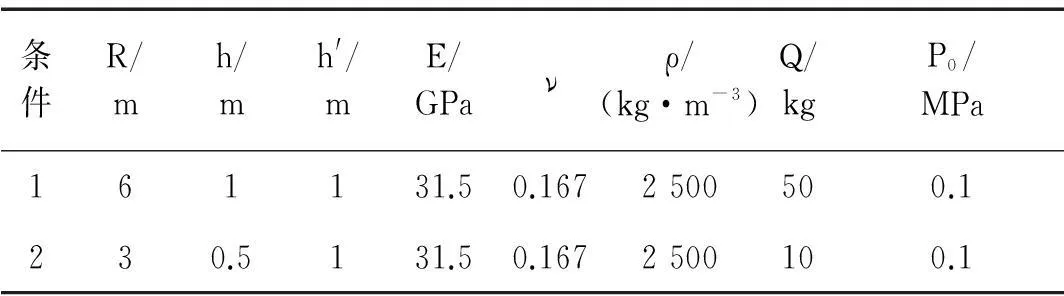
表1 计算参数

本文方法与文献[6]方法计算的柱壳轴向各点径向最大位移见图5。其中图5(a)~5(c)按简化及精确方法所得结果均为前五阶振型位移叠加解,图5(d)为按模型二简化计算的第一阶振型位移解。文献[6]方法由于只考虑第一振型,所得位移峰值偏小;模型一选
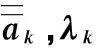
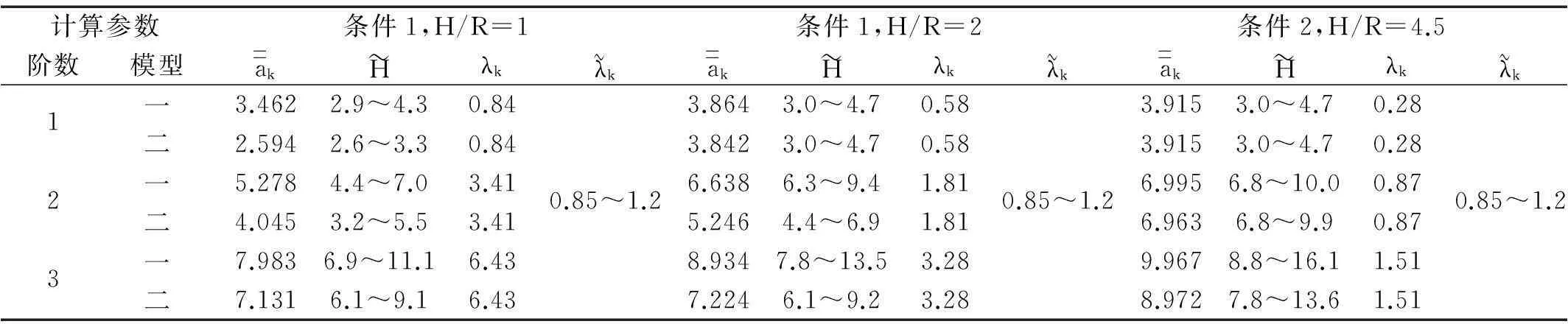
表2 频率参数 计算值
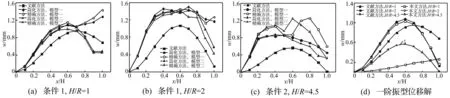
图5 沿柱壳轴向分布径向位移最大值 Fig.5 Graph of radial displacement maximum value along axial direction of cylindrical shell
图6为柱壳某点处径向位移时程图。由图6看出,H/R=1时两种模型与文献[6]结果较一致,均出现在振动第一个周期,模型一精确解与文献[6]方法解相差不大,表明结构振动以第一振型为主,模型二精确解在达峰值后开始衰减,表明顶端集中质量对径向振动影响;随H/R的增大,按两种模型计算的精确解逐渐大于文献[6]计算值,说明第一振型位移在总位移中所占比例减小,且由于轴向、径向振动频率耦合,峰值位移
达时间tr向后推迟,见图6(b)中tr=25 ms,图6(c)中tr=42 ms,图6(d)中tr=39 ms,此时采用文献[6]方法计算则会产生较大误差;图6(d)显示在接近柱壳顶部位置,模型二计算位移峰值小于模型一,体现出集中质量对壳体振动影响。
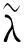

(a) H/R=1,x/H=0.7 (b) H/R=2,x/H=0.6 (c) H/R=4.5,x/H=0.6 (d) H/R=4.5,x/H=0.9 图6 圆柱壳内壁径向位移时程图 Fig.6 Time-history graph of radial displacement of cylindrical shell inner wall
计算参数条件1,H/R=1条件1,H/R=2条件2,H/R=4.5阶数模型akHλkλkakHλkλkakHλkλk1一3.4622.9~4.30.843.8643.0~4.70.583.9153.0~4.70.28二2.5942.6~3.30.843.8423.0~4.70.583.9153.0~4.70.282一5.2784.4~7.03.410.85~1.26.6386.3~9.41.810.85~1.26.9956.8~10.00.870.85~1.2二4.0453.2~5.53.415.2464.4~6.91.816.9636.8~9.90.873一7.9836.9~11.16.438.9347.8~13.53.289.9678.8~16.11.51二7.1316.1~9.16.437.2246.1~9.23.288.9727.8~13.61.51
图7为不同长径比时壳体中部x/H=0.5与近顶端x/H =0.9处的轴向位移时程图。其中简化解为前五阶位移解之和,精确解则为在简化解中加入按模型二计算的径向荷载产生的轴向位移ur。由图7(a)看出,H/R=1时简化解与精确解相差不大,表明由径向荷载产生的轴向位移ur对总轴向位移u贡献不大,轴向振动主要以振型式(11)为主,且u的最大值位移柱壳顶端;长径比增大时ux对u贡献减小,而ur在总位移u中所占份额逐渐增大,见图7(e)、(f),表明顶端作用力对柱壳振动影响随H/R的增大逐渐减弱。
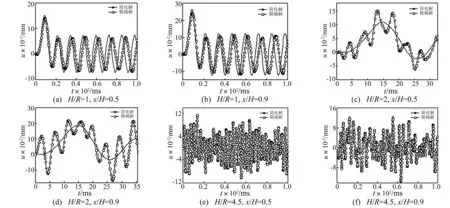
图7 壳体内壁轴向位移时程图 Fig.7 Time-history graph of axial displacement of cylindrical shell inner wall
4结论
(1)对具有球形顶盖的圆柱壳结构,内爆炸条件下柱壳同时承受径向及轴向荷载,径向动载作用时按底端固支、顶端铰支边界含集中质量的梁振型计算柱壳振动位移;轴向动载作用时按底端固支、顶端自由边界含集中质量的杆振型计算,两种荷载作用下结构位移叠加即获得总振动位移。



参考文献
[1]穆朝民,任辉启,李永池,等.爆室内爆炸流场演化与壳体动力响应研究[J].振动与冲击, 2009,28(10):106-111.
MU Chao-min, REN Hui-qi, LI Yong-chi, et al. Blast flow field evolution and dynamic response of a blast chamber [J]. Journal of Vibration and Shock, 2009,28(10):106-111.
[2]穆朝民,任辉启,李永池,等.爆室内爆炸流场演化与壳体动力响应的数值模拟[J].弹箭与制导学报,2010,30(2): 82-86.
MU Chao-min, REN Hui-qi, LI Yong-chi, et al. Numerical simulation on blast flow field evolution and dynamic response of blast chamber[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(2):82-86.
[3]年岗.内爆炸载荷作用下密闭爆炸容器振动特性研究[D].南京: 南京理工大学, 2011.
[4]王天运,任辉启,王玉岚.接触爆炸荷载作用下核电站安全壳的动力响应分析[J].核动力工程,2005,26(2): 187-195.
WANG Tian-yun, REN Hui-qi, WANG Yu-lan. Analysis of dynamical response of nuclear power plant concrete containment under contact blast load[J]. Nuclear Power Engineering, 2005, 26(2):187-195.
[5]刘云飞,王天运,贺锋,等.核反应堆预应力钢筋混凝土安全壳内爆炸数值分析[J].工程力学,2007,24(8): 168-172.
LIU Yun-fei, WANG Tian-yun, HE Feng, et al. Numerical simulation for pre-stressed concrete containment under internal explosive loading[J]. Engineering Mechanics, 2007, 24(8): 168-172.
[6]李杰.特种建筑物抗爆安全与防护评估[D].南京:解放军理工大学,2007.
[7]程志军,李杰,宋春明,等.特种结构物内爆炸动力响应分析[J].振动与冲击,2013,32(6):96-99.
CHENG Zhi-jun, LI Jie, SONG Chun-ming, et al. Dynamic response analysis of special structures under inner explosion[J]. Journal of Vibration and Shock,2013, 32(6): 96-99.
[8]Timoshenko S, Woinowsky-Krieger S. Theory of plates and shells[M]. New York: McGraw-Hill Book Company, Inc., 1959.
[9]曹志远.板壳振动理论[M].北京:中国铁道出版社,1986.
[10]奥尔连科,著.孙承纬,译.爆炸物理学[M].北京:科学出版社,2011.
[11]Котляревский В А, Ганушкин В И, Костин А А,et al. Убежища гражданской обороны. Конструкции и расчет [М]. Москва: Стройиздат, 1989.



