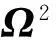智能柔性构件振动改进多模态正位置反馈控制
第一作者娄军强男,博士生,1986年生
通信作者魏燕定男,教授,博士生导师,1970年生
智能柔性构件振动改进多模态正位置反馈控制
娄军强1,魏燕定2,杨依领2,谢锋然2,赵晓伟2(1.宁波大学浙江省零件轧制成形技术研究重点实验室,浙江宁波315211; 2. 浙江大学现代制造工程研究所,杭州310027)
摘要:为实现较少致动器数目下柔性构件多个振动模态的主动控制,基于力学原理及模态理论建立智能柔性构件动力学方程。在研究单模态PPF控制器性能特点及稳定条件基础上,提出考虑不同模态权重的改进多模态PPF控制器。采用根轨迹法分析系统的闭环阻尼特性确立各阶PPF控制器最佳控制参数并进行数值仿真;搭建实验平台验证相关分析及控制策略的有效性。结果表明,所提考虑模态权重的改进多模态PPF控制器利用单组致动器能有效抑制柔性梁构件的多阶振动模态、显著缩短柔性构件振动的衰减时间。实验中柔性构件的衰减时间由6 s减少为2.5 s。实现较少数目致动器下柔性构件多阶弹性模态的振动主动控制。
关键词:智能柔性构件;改进正位置反馈;振动主动控制;压电致动器
基金项目:国家自然科学
收稿日期:2014-02-08修改稿收到日期:2014-04-30
中图分类号:TP24;TB32文献标志码:A
基金项目:国家863计划项目(2011AA11A265);国家自然科学基金(51205290);中央高校基本科研业务费专项资金项目(1700219118)
Modified multi-mode positive position feedback controller for active vibration controlof a smart flexible structure
LOUJun-qiang1,WEIYan-ding2,YANGYi-ling2,XIEFeng-ran2,ZHAOXiao-wei2(1. Zhejiang Provincial Key Lab of Part Rolling Technology, Ningbo University, Ningbo 315211, China; 2. Research Institute of Contemporary Manufacturing Engineering, Zhejiang University, Hangzhou 310027, China)
Abstract:To actively suppress multi-mode vibration of a structure with less actuators, the dynamic model of a smart flexible structure was derived based on the mechanical principle and modal theory. Characteristics and stability condition for a single-mode positive position feedback (PPF) controller were studied, and then a modified multi-mode PPF controller considering different weights of each mode was proposed. Damping characteristics of a close-loop system was acquired with the root locus method, the optimal parameters for each mode of the PPF controller were determined. After some numerical simulations, the test platform was set up. The validity and feasibility of the proposed controller were demonstrated with the simulation and test results. It was shown that the multi-mode vibration of the structure with the modified multi-mode PPF controller is significantly reduced using only a pair of piezoelectric actuators, and its damping decay time is shortened to 2.5 s from 6 s. So the multi-mode vibration of the flexible structure was well suppressed using less piezoelectric actuators.
Key words:smart flexible structure; modified positive position feedback; active vibration control; piezoelectric actuators
随工业技术与机器人技术水平提高,质量轻、功耗少、载荷/自重比高柔性构件在工业生产、土木工程、交通运输及航空航天等领域获得广泛应用[1]。柔性构件低刚度、低阻尼特性导致其在外界激励下较易激起自身的弹性振动,对柔性构件建模及振动控制技术研究成为动力学及控制学的研究热点[2]。近年来,压电材料、记忆合金及磁流变液等智能材料为柔性构件的振动控制技术提供了新途径,尤以频响宽、响应速度快、埋入粘贴均较方便的压电材料使用最多[3]。
基于压电材料的智能柔性构件振动控制技术研究中,速度负反馈及变结构控制等技术均应用较多,且取得较好控制效果[4]。柔性构件的弹性振动本质上由无穷模态叠加组成,而实际中为简化控制结构、节约控制成本,常采用模型降阶技术,仅对柔性构件几阶重要模态进行控制研究,导致控制/观测溢出现象发生,甚至系统失稳。Shan等[5]将具有高阶模态不敏感性及良好鲁棒性的正位置反馈控制技术(Positive Position Feedback, PPF)引入柔性构件控制中。邱志成等[6-7]利用PPF控制技术分别实现柔性梁构件及板构件的振动主动控制。如何确保PPF控制系统稳定性,尤其控制多个模态多个PPF控制器同时工作[8],尚需据实际系统特性深入研究。为节约控制成本,如何以较少数目致动器实现柔性构件多模态同时控制仍需深入探索。
1系统建模
实际中较多柔性构件均为细长均质的薄壁杆件,可视为Euler-Bernoulli梁模型。上下表面粘贴压电致动器及应变传感器的柔性梁构件模型见图1。一对尺寸为lp×bp×hp的压电陶瓷片作为致动器对称粘贴于长×宽×高为lb×bb×hb的柔性梁构件上下表面;在近致动器位置布设一对应变传感器组成桥接电路用于检测梁的振动。
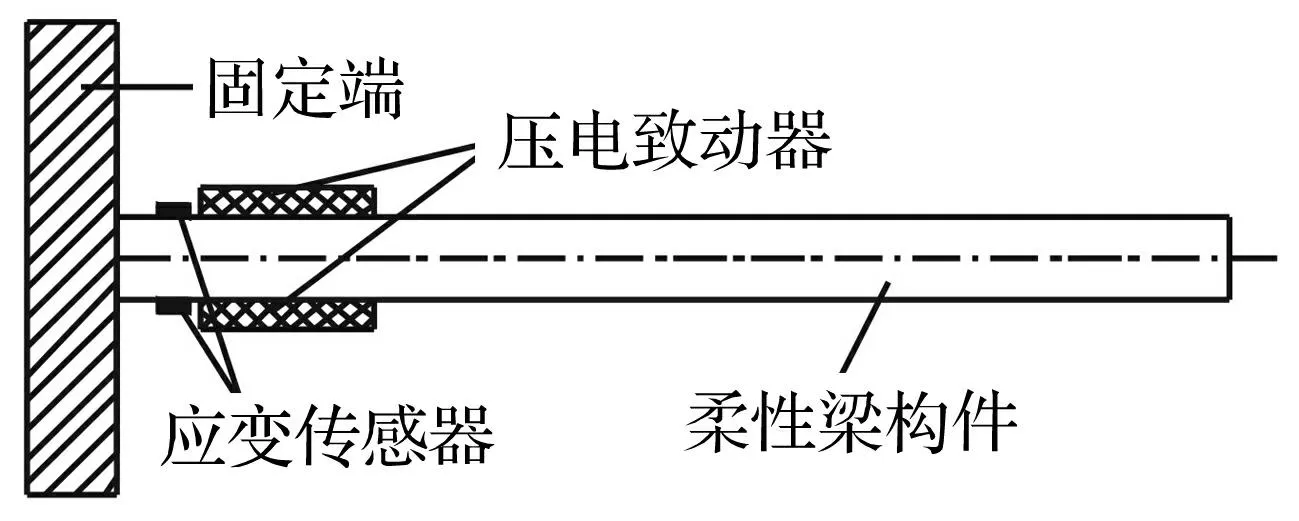
图1 贴有致动器/传感器的柔性梁构件模型 Fig.1 A flexible structure with actuators and sensors
据牛顿力平衡原理及欧拉梁变形假设,当控制电压施加于压电致动器时,智能柔性梁构件的横向振动动力学方程用偏微分方程(PDE)表示[9]为
(1)
式中:w(x,t)为梁构件横向振动位移;ρb, Ab, Eb, Ib分别为梁构件体密度、横截面积、弹性模量及惯性矩;M(x,t)为压电致动器控制力矩。
为获得梁的模态函数,设其处于自由振动状态,采用变量分离法得
w(x,t)=φ(x)q(t)
(2)
式中:φ(x)为关于位移变量x的模态振型函数;q(t)为关于时间变量t的横向位移函数。
对图1的梁构件模型,采用一端固定一端自由的边界条件,得第i阶固有频率为
(3)
式中:βilb为梁构件的第i阶特征频率。
若将所有阶次模态叠加,可得柔性梁构件的自由振动响应为
(4)
致动器与构件理想粘贴情况下,控制力矩为
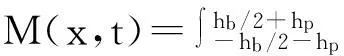
d31bpEp(hb+2hp)V(x,t)=kpV(x,t)
(5)
式中:d31为压电陶瓷材料的压电应变常数;kp为压电致动器的等效电压系数;H(·)为关于空间坐标x的Heaviside函数;xs, xe为致动器起始及终止位置;V(t)为驱动电压,具体表达式为
V(x,t)=V(t)[H(x-xe)-H(x-xs)]
(6)
将式(4)~式(6)结果代入式(1),据模态正交性及Heaviside函数特性,加入结构阻尼影响,得梁构件解耦形式的常微分模态方程为
(7)
式中:ξi为梁构件第i阶模态阻尼比;Ψi为与压电致动器位置相关函数,可表示为
(8)
按图1方式粘贴传感器,采用半桥接法获得应变传感器的电压即系统输出为
(9)
式中:ε为传感器灵敏度系数;U0为传感器桥接电路的供桥电压;ks为传感器输出系数。
2控制器设计
2.1单模态PPF控制器特性及稳定性
实际中柔性构件的弹性振动往往以低阶模态为主,故仅需重点关注一定频带范围内的振动模态。在设计多模态PPF控制器之前,先描述单模态PPF控制器行为的动力学方程[10]为
(10)
式中:q, ζ, ω分别为被控结构的广义模态坐标、阻尼比及固有频率;η, ζc, ωc分别为PPF控制器广义坐标、阻尼比及固有频率;g为PPF控制器控制增益。此时系统稳定的充分必要条件为0 通过Laplace变换得式(10) 的PPF传递函数为 (11) 由式(11)看出,PPF控制器实际为二阶低通滤波器,亦称PPF滤波器[12],具有高频剪切特性。此即PPF控制器对特定频率具有主动阻尼控制效果原因。 2.2考虑模态权重的改进多模态PPF控制器 即使采用模态截断技术,柔性构件的弹性振动仍由一定数目振动模态组成,且有时会出现多个主模态。为同时抑制多模态振动,需对每个振动模态分别设计PPF控制器,多个PPF控制器并行工作;而随之产生系统稳定条件更复杂、更难达到较好控制效果等问题。 对式(7)保留n阶模态的柔性构件模型,采用相同数目PPF控制器,结合传感器输出式(9)及致动器电压输入式(5),得柔性构件及PPF控制器方程为 (12) 式中:Kc为致动器控制电压模态系数矩阵;Ks为传感器输出电压模态系数矩阵;Q=[q1, q2, …, qn]T为结构模态向量;E=[η1, η2, …, ηn]T为PPF控制器状态向量;Zs=diag[ζ1, ζ2, …, ζn]为结构阻尼矩阵;G=[g1, g2, …, gn]为控制增益向量;Zc=diag[ζc1, ζc2, …, ζcn]为PPF控制器阻尼矩阵;Ωs=diag[ω1, ω2, …, ωn]为结构频率矩阵;Ωc=diag[ωc1, ωc2, …, ωcn]为PPF控制器频率矩阵。 定理:针对式(12)的闭环控制系统结构,系统稳定的充分必要条件为 (13) 虽然式(12)表明柔性构件多模态闭环控制系统在广义模态坐标上是解耦的,但致动器的实际控制电压通过模态控制力计算获得,实际控制系统为内在解耦外在耦合。尤其考虑压电致动器数目及控制力矩有限,往往希望将致动器的控制力主要作用于占比重较大的主模态。因此利用PPF控制器对多个模态并行控制,此处以反映各阶模态衰减速度的振动频率及阻尼乘积作为衡量各阶PPF控制器输出的权衡指标,提出权重系数 (14) 确定的改进多模态PPF控制器结构见图2。为防止致动器驱动电压过大,加入电压饱和模块。需指出的是,虽通过系统稳定性条件(式(12))可确定控制增益G的取值,但由于实际中致动器输入及传感器输出的模态系数精确值较难获得,故仍需具体数值分析及实验验证才能得到较好的控制效果。 图2 考虑模态权重的改进PPF控制器结构图 Fig.2 Structure of a modified PPF controller 2.3PPF控制器参数设计及计算 本文所用柔性梁构件及压电致动器尺寸、特性参数见表1。此处仅对柔性构件的前两阶振动模态进行研究。理论计算得前两阶固有频率分别为24.5 rad/s (3.9 Hz)及153.5 rad/s (24.4 Hz)。设模态阻尼比为0.02及0.008。由式(12)看出,控制各阶模态的PPF控制器由ωc, ζc及g决定。为实现较少数目致动器下柔性构件多模态振动控制,重点考察一组致动器的振动控制效果,从控制效果、控制鲁棒性两方面考虑[13],选对应的两阶PPF控制器阻尼ζc分别为0.6及0.4。 表1 柔性梁构件及压电致动器基本参数 为确定对应两阶振动模态的两个PPF控制器其它参数,采用独立设计方法。 (15) 对控制柔性构件一阶模态的PPF控制器,其频率及结构模态频率满足表达式(15)时,控制增益g1从0变化到无穷大过程中,对应的闭环系统根轨迹曲线见图3。 图3 闭环系统的根轨迹图 Fig.3 Root locus diagram of close-loop system 由图3看出,当g在一段特定范围内取值时,根轨迹曲线与虚轴平行,系统的闭环极点具有相同实部,且所有根轨迹曲线交汇于一点,该点与系统闭环衰减特性密切相关。当控制增益g取不同值时,系统一阶模态闭环极点的负实部随系统结构频率ω1变换关系见图4。由图4看出,对每个固定增益g,系统的衰减特性均由上、下两支组成。当增益大于某一值时(g≥0.36),所有曲线均相交于一点,即根轨迹交点,此时系统具有最大的闭环阻尼。因此可设定一阶PPF控制器频率稍大于柔性结构一阶固有频率,从而保证以最小的控制增益实现最大闭环阻尼,使系统振幅最小、控制效果最优[14]。 图4 一阶PPF控制下系统闭环衰减特性 Fig.4 Damping characteristics with 1st PPF controller 对控制柔性构件二阶模态振动的二阶PPF控制器采用同样设计方法,所得系统二阶模态的闭环衰减特性见图5,显然g取最小值0.16时系统闭环增益最大。由图4、图5看出,当g大于1时闭环衰减特征曲线无交点,系统处于不稳定状态。 图5 二阶PPF控制下系统闭环衰减特性 Fig.5 Damping characteristics with 2nd PPF controller 确定的两阶PPF控制器基本参数见表2。 表2 各阶PPF控制器的基本参数 3数值仿真 仿真分析中,设系统初始状态q0=[0.01 0.006]。为对比不同控制增益下各阶PPF控制器的控制效果,不同控制增益的一阶PPF控制器对柔性构件一阶振动模态控制效果见图6。由图6看出,当g取值(g=0.2)小于最优增益(g=0.36)时,PPF控制器的控制作用随之减弱;而当g取值(g=0.5)大于最优控制增益时,控制器的控制效果基本无变化。由此证明g取0.36时系统一阶振动模态具有最大闭环阻尼,控制效果最佳。 图6 一阶PPF控制器单独作用下的模态位移曲线 Fig.6 Modal displacement with 1st PPF Controller 不同控制增益二阶PPF控制器对柔性构件二阶振动模态的控制效果见图7,同样可得g取0.16时系统二阶振动模态具有最大的闭环阻尼,控制效果最佳之结论,与理论推导结果一致。 图7 二阶PPF控制器单独作用下模态位移曲线Fig.7ModaldisplacementwitpndPPFController图8 多模态PPF控制器作用下模态位移曲线Fig.8Modaldisplacementwithmuliti-modePPFControllers 考虑不同模态权重的改进多模态PPF控制下柔性构件模态位移曲线及与相同权重多模态PPF控制器控制效果对比见图8。仿真结果表明,改进的多模态PPF控制器由于给予系统一阶模态更高权重,致动器控制力更多用于对一阶模态控制,因而柔性梁构件一阶振动模态抑制效果更好。虽二阶振动衰减效果稍有下降,但仍得到有效控制,柔性构件多模态振动在改进的多模态PPF控制下衰减较快。 4实验验证 为验证所提控制方法的可行性及控制效果,搭建智能柔性构件实验测控系统见图9。实验中利用粘贴在构件根部的应变传感器检测柔性梁构件振动信息,传感器输出电压信号经信号放大器(自制,放大增益5 000)放大为-10~+10的电压信号,通过截止频率为35 Hz的巴特沃斯低通滤波器滤波后,经多路数据采集卡(研华 PCI-1742U)输送至工控机;利用NI-LabVIEW编写测控软件采用改进的多模态PPF控制器计算获得致动器的控制信号,通过采集卡的D/A模块输出并经功率放大器(自制,放大倍数15)放大为-150~+150V的电压信号,作用于压电致动器,驱动压电致动器按所设控制律实现柔性构件多模态振动的主动控制。贴有压电致动器/传感器的柔性梁构件实物见图10。 图9 智能柔性构件实验测控系统结构图 Fig.9 Schematic diagram of the experimental system 图10 贴有致动器/传感器的柔性梁构件实物图 Fig.10 Photo of the flexible structure with actuators and sensors 利用冲击锤敲击激起柔性构件的弹性振动以测定其模态特性,传感器输出信号经放大后见图11(a),将该信号进行FFT变换所得频域信号见图11(b)。经计算获得梁构件前两阶模态频率为17.2 rad/s(2.73 Hz)及110.0 rad/s(17.5 Hz),与理论计算结果有一定差异,主因在理论分析中未考虑粘贴的压电片及引出导线对柔性梁构件质量、刚度影响所致,且梁构件的实际参数特性与标称值亦存差异,因此对两PPF控制器参数进行适当修正调整。 图11 应变传感器的输出信号Fig.11Outputsignalsofthestrainsensors图12 相同权重多模态PPF控制下传感器输出信号Fig.12Comparedoutputsignalsofthesensorswiththestandardmulti-modePPFcontroller图13 改进多模态PPF控制下传感器输出信号Fig.13Comparedoutputsignalsofthesensorswiththemodifiedmulti-modePPFcontroller 为检验设计的多模态PPF控制器控制效果,采用相同权重的多模态PPF控制器对柔性梁构件(图10)进行抑振控制研究。应变传感器输出的时、频域信号见图12。与自由衰减状态相比,柔性构件振动在设计的多模态PPF控制器下得到快速衰减,一、二阶振动模态均得到有效抑制(图12(b)),且振动衰减时间从6 s缩短为3.5 s(图12(a))。 由图11(b)及图12(b)看出,柔性梁一阶振动模态在实验冲击信号激励下占主导地位。为得到更好的控制效果,进行柔性梁构件在设计的改进多模态PPF控制器下的实际抑振控制实验,结果见图13。由图13知,较相同权重的多模态PPF控制实验结果,改进多模态PPF控制器因通过设置不同模态控制权重将更多控制力用于控制占主导地位的一阶振动模态,振动抑制效果更好,进一步缩短柔性构件的振动抑制时间约为2.5。因此本文考虑模态权重的多模态PPF控制器符合实际且合理有效,利用单组压电致动器能实现柔性构件多模态的有效控制。 5结论 (1)通过建立智能柔性梁构件系统动力学模型,在分析单模态PPF控制器特点及稳定条件基础上,提出考虑不同模态权重的改进多模态PPF控制器。利用轨迹法分析整个控制系统的闭环阻尼特性,确立各阶PPF控制器最佳控制参数,通过数值仿真及实验验证了相关分析及控制策略的有效性。 (2)仿真及实验结果表明,本文考虑模态权重的改进多模态PPF控制器能有效抑制柔性梁构件的多阶振动模态、显著缩短构件振动衰减时间(6 s缩短为2.5 s)。为解决较少数目致动器下柔性构件多阶振动模态的控制提供了有益的借鉴及尝试。 参考文献 [1]贾鹏霄, 李恩, 梁自泽, 等. PD自适应控制结合输入整形抑制单模态弹性机构振动研究[J].振动与冲击,2013,32(17):189-193. JIA Peng-xiao, LI En, LIANG Zi-ze, et al. Adaptive PD control combined with input-shaping for suppressing vibration of a single-mode flexible mechanism [J]. Journal of Vibration and Shock, 2013, 32(17):189-193. [2]Jovanovic M M, Simonovic A M, Zoric N D, et al. Experimental studies on active vibration control of a smartcomposite beam using a PID controller[J]. Smart Materials and Structures, 2013, 22:1-8. [3]李磊, 魏燕定, 陈子辰, 等. 机敏杆压电扭转驱动器/传感器优化布置[J]. 振动与冲击, 2008,27(10):148-151. LI Lei, WEI Yan-ding, CHEN Zi-chen, et al. Optimal placement of piezoelectric torsional actuator/sensor based on smart bar[J]. Journal of Vibration and Shock, 2008,27(10):148-151. [4]Fisco N R, Adeli H. Smart structures:part I-active and semi-ctive control[J]. Scientia Iranica, 2011, 18(3): 275-284. [5]Shan J J, Liu H T, Sun D. Slewing and vibration control of a single-link flexible manipulator by positive position feedback (PPF)[J]. Mechatronics, 2005, 15(4): 487-503. [6]邱志成. 刚柔耦合系统的振动主动控制[J]. 机械工程学报, 2006,42(11): 26-33. QIU Zhi-cheng. Activevibration control for coupling system of flexible structures and rigid body[J]. Chinese Journal of Mechanical Engineering, 2006, 42(11): 26-33. [7]Mahmoodi S N, Ahmadian M, Inman D J. Adaptivemodified positive position feedback for active vibration control of structures[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(6): 571-580. [8]Fanson J L, Caughey T K. Positive position feedback control for large space structures[J]. AIAA Journal, 1990, 28(4): 717-724. [9]Spier C, Jr Bruch J C, Sloss J M, et al. Effect of vibration control on the frequencies of a cantilever beam with non-ollocated piezo sensor and actuator[J]. Intelligent Control Theory and Applications, 2011, 5(15): 1740-1747. [10]Reis J C P, Da Costa J S. Motion planning and actuator specialization in the control of active-flexible link robots[J]. Journal of Sound and Vibration, 2012, 331(14): 3255-3270. [11]杨拥民, 张华, 胡政. 正位置反馈的多模态振动主动控制实验[J]. 振动工程学报, 2005, 18(3): 355-359. YANG Yong-min, ZHANG Hua, HU Zheng. Positive position feedback based active vibration control of multiple modes[J]. Journal of Vibration Engineering, 2005, 18(3): 355-359. [12]Kwak M K, Heo S. Active vibration control of smart grid structure by multi-input and multi-output positive position feedback controller[J]. Journal of Sound and Vibration, 2007, 304(1/2): 230-245. [13]Goh C J, Caughey T K. On the stability problem caused by finite actuator dynamics in the collocated control of large space structures[J]. International Journal of Control, 1985, 41(3): 787-802. [14]Mahmoodi S N, Ahmadian M. Active vibration control with modified positive position feedback[J]. Journal of Dynamic Systems Measurement and Control, 2009, 131:1-8.