中央开槽箱梁涡激共振特性及抑振措施机理研究
第一作者杨婷女,硕士生,1989年生
通信作者周志勇男,博士,研究员,博士生导师,1972年生
邮箱:z.zhou@tongji.edu.cn
中央开槽箱梁涡激共振特性及抑振措施机理研究
杨婷,周志勇(同济大学土木工程防灾国家重点实验室,桥梁结构抗风技术交通行业重点实验室,上海200092)
摘要:基于大比例节段模型风洞测振、测压试验及计算流体力学(Computational Fluid Dynamic,CFD)方法进行中央开槽箱梁涡激共振特性及抑振措施机理研究。以芜湖长江公路二桥为例进行大比例节段模型风洞试验。结果显示,位于气动敏感位置内侧检修车轨道是诱发涡激共振原因。CFD数值模拟表明,流过上游断面底板的气流遭遇内侧检修车轨道阻挡,会加大上游断面尾流死水区宽度,开槽区域产生连续旋涡脱落现象,主导主梁断面涡振发生。提出将内侧检修车轨道向主梁中心线偏移一定距离方案,使上游断面流过梁底的高速气流在底板内侧转角处不受检修车轨道影响,气流分离点延后,开槽区域连续旋涡脱落现象消失。主梁断面表面静态测压试验结果显示,此时气流沿梁体外形能平稳过渡,无明显流动分离现象,上游断面底板内侧转角处负压值不会产生剧烈突变。上、下游断面整个内腹板的脉动压力减小、能量分散,无一致的卓越频率。对改进断面进行大比例节段模型涡振风洞试验,并与原型断面结果对比,证实其为有效的抑振措施。
关键词:涡振;机理研究;CFD;中央开槽箱梁;检修车轨道;大比例节段模型试验
收稿日期:2014-01-28修改稿收到日期:2014-05-16
中图分类号:U448.27文献标志码:A
Vortex-induced resonance characteristics and anti-vibration measures’ mechanism of central-slotted box girders
YANGTing,ZHOUZhi-yong(State Key Laboratory for Disaster Reduction in Civil Engineering, Transport Industry Key Laboratory for Wind ResistanceTechnique in Bridge Engineering, Tongji University, Shanghai 200092, China)
Abstract:To study vortex-induced resonance characteristics and anti-vibration measures’ mechanism of central- slotted box girders, the large-scale sectional model vibration measurement, pressure measurement and CFD were employed. A long-span cable-stayed bridge over Yangtze River was taken as an example to conduct wind tunnel tests of large-scale sectional model. The test results indicated that it is the maintenance rails located inside aerodynamic susceptible sites that cause the vortex-induced vibration of the bridge. CFD numerical simulation results showed that the upwind flow passing through the curved soffit plate is hindered by the inside maintenance rails to cause an increased width of dead water region in the wake of upwind box section, a continuous and intensive vortex shedding phenomenon occurs due to velocity gradient and the VIV of the bridge main beam section takes place; accordingly, the inside maintenance rails are proposed to offset the center line of the main beam with a certain distance, they are not an obstacle to the high-speed upwind flow; thus the flow separates at the location far away from the knuckle line and the size of dead water region in the upwind box wake is reduced to prevent the vortex shedding. The static pressure test results showed that when shifting the inside maintenance rails, the negative mean pressure at the soffit plate knuckle line, does not change dramatically, the fluctuating pressures on the upwind and downwind inclined panels can be reduced, and the fluctuating energy is dispersed without a consistent predominant frequency. Wind tunnel tests for the modified section were conducted and the results showed that the VIV of the bridge can be suppressed completely.
Key words:vortex-induced vibration (VIV); mechanism research; CFD; central-slotted box girders; maintenance rails; large-scale sectional model test
大跨度桥梁中央常采用开槽形式,如西堠门大桥(B/H≈10)、香港昂船洲大桥(B/H≈13.5)、南京右汊大桥(B/H≈13.5)、杭州湾嘉绍大桥(B/H≈14)、青岛海湾大桥大沽河航道桥(B/H≈13)、港珠澳大桥江海直达船航道桥(B/H≈10)等。据已有工程及研究经验,开槽有助于提高颤振临界风速,但会使上游断面尾部变钝,常诱发涡振。因此需对该类桥梁的涡振特性进行风洞试验及数值模拟研究。
Larose等[1]在对昂船洲大桥分体钢箱梁进行一系列涡振试验认为,梁底气流经导流板后可形成速度压缩,能干扰中央开槽处形成能量较大旋涡,抑制规律性旋涡对结构的驱动,达到制振目的。Matsuda等[2]用1∶10中央开槽断面节段模型对不同雷诺数下进行定常与非定常气动力系数分析表明,80°风嘴及有无格栅两种开槽断面均发生雷诺数效应,表现为St数及压力分布不同;低雷诺数下风洞试验结果偏保守。李玲瑶等[3]采用大比例节段模型试验方法对两种导流板设置方案的涡振控制效果对比结果表明,中央开槽断面的涡振性能较差,导流板涡振控制效果除与原断面气动外形及槽宽有关外,与导流板高度、长度、倾角密切相关。欧阳克俭等[4]通过1:50节段模型试验,对中央开口断面悬索桥进行涡振控制风洞试验表明,在人行道板下加底板使桥梁断面在人行道处形成光滑过渡,能有效抑制涡振。廖海黎等[5]通过1:60与1:20两种比例节段模型试验,研究分体式钢箱梁斜拉桥的涡激振动特性和相应制振措施表明,背风侧底板内侧转角区为主梁的气动敏感区,在此处安装导流板能干扰旋涡形成,起到制振作用。汪正华等[6]采用大比例节段模型风洞试验,研究中央开槽主梁的涡激振动特性,分析不同格栅板样式及空隙率对随风速变化的涡振振幅影响知,格栅板空隙率越小抑制涡振效果越好。孟晓亮等[7]通过1:80节段模型风洞试验比较检修车轨道位置改变引起半封闭分离双箱梁涡激共振特性表明,检修车轨道位置变化因改变主梁断面气动外形而影响主梁的涡振性能。王骑等[8]采用1:60与1:20两种比例节段模型试验,分析分体式钢箱梁的涡振特性、验证导流板与抑振板的制振效果。Larson等[9]通过1:20节段模型测压试验,对昂船洲大桥进行导流板制振机理分析表明,上游断面的压力脉动源于底板内侧转角处形成的旋涡脱落,下游断面的压力脉动源于上游产生的旋涡对其造成的冲击力。下游断面压力脉动值远大于上游断面脉动值,约为3~4倍。Li等[10]运用POD方法对现场实测的分离双箱悬索桥平均压力及脉动压力进行分析,观察断面周围流体的时间-空间变化特性知,规律的涡脱现象一开始只发生在开槽区域及下游断面尾流区域;进入锁定区间后随主梁振动涡脱现象随之剧烈,区域扩展到整个下游断面底表面与上游断面的尾流区域,开槽区域及梁底表面区域涡区聚在一起。Kwok等[11]对5种带不同槽宽的分离双箱梁进行表面测压风洞试验,所得不同风攻角下梁体表面平均压力值与压力脉动值分布表明,槽宽大小会极大影响梁体表面压力分布及St数,揭示出涡振机理。Watanabe等[12]运用LES湍流模型对中央开槽断面进行三维非定常静力计算,实现流场可视化,结果表明,主梁迎风侧风嘴下缘产生的流动分离与再附现象导致升力系数、升力矩系数增大;若主梁断面在大风攻角下能使迎风侧风嘴处流动分离不易产生,则能保证其在大部分风攻角下的气动稳定性。Laima等[13]对分离双箱梁节段模型进行静、动态测试风场试验,观察旋涡脱落现象,并结合数值模拟方法分析涡振发生时表面压力分布、流体与模型间动能传递、流态演变。结果显示,涡结构主要聚集于下游主梁的迎风腹板位置。何晗欣等[14]通过1∶45节段模型试验及CFD分析,研究中央开槽箱型断面的三种气动措施(增设不同开孔率底板、改变腹板角度、增设导流板)的有效性。
本文以在建安徽芜湖长江公路二桥为研究背景,采用大比例节段模型风洞试验、表面压力同步测量及CFD数值模拟方法,从宏观、微观两方面对中央开槽箱梁断面涡振机理进行分析,提出具体气动措施,以涡振试验结果、主梁断面表面压力分布特性及CFD计算所得流场形态,共同验证气动措施的有效性。
1工程背景与试验概况
1.1桥梁概况
芜湖长江公路二桥为双塔四索面斜拉桥,桥跨布置为100+308+806+308+100(m),主桥全长1 622 m,整体布置见图1。斜拉桥采用密索半漂浮结构体系,斜拉索采用平行钢丝索扇形空间索面布置形式,两主塔桥面以上高度210.4 m。加劲梁为全宽53 m、槽宽17 m、梁高3.5 m的中央开槽式的双闭口流线型钢箱梁,由每隔32 m的横梁连接成整体。主梁宽高比B/H=15.1,槽宽与梁宽比b/B=0.32。主梁外侧底板采用弧形的鱼腹型曲线,避免梁体出现明显的气动分离点。中央开槽主梁标准断面见图2。
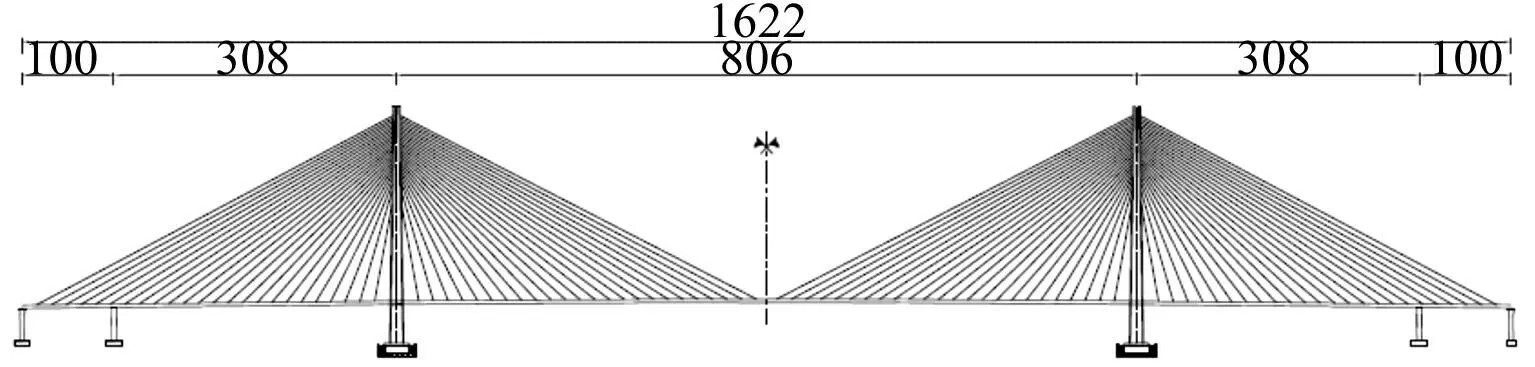
图1 桥梁立面图(单位:m) Fig.1 General layout of the cable-stayed bridge (unit:m)
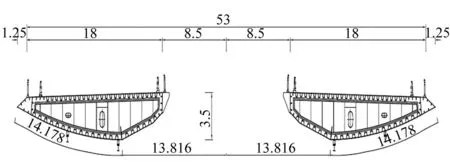
图2 中央开槽主梁横断面图(单位:m) Fig.2 Cross section of the bridge deck (unit:m)
1.2大比例节段模型试验

图3 节段模型试验装置图 Fig.3 Sketch of the testing device
试验在同济大学TJ-3风洞中进行。该风洞试验段长15 m,宽14 m,高2 m,试验风速范围为0~17 m/s连续可调,均匀流场紊流度≤0.3%。为使试验雷诺数较大、精确模拟箱梁构造细节及试验结果接近实际,设计制作几何缩尺比为1∶22,长度为7.3 m的大比例节段模型(长宽比>3),见图3。
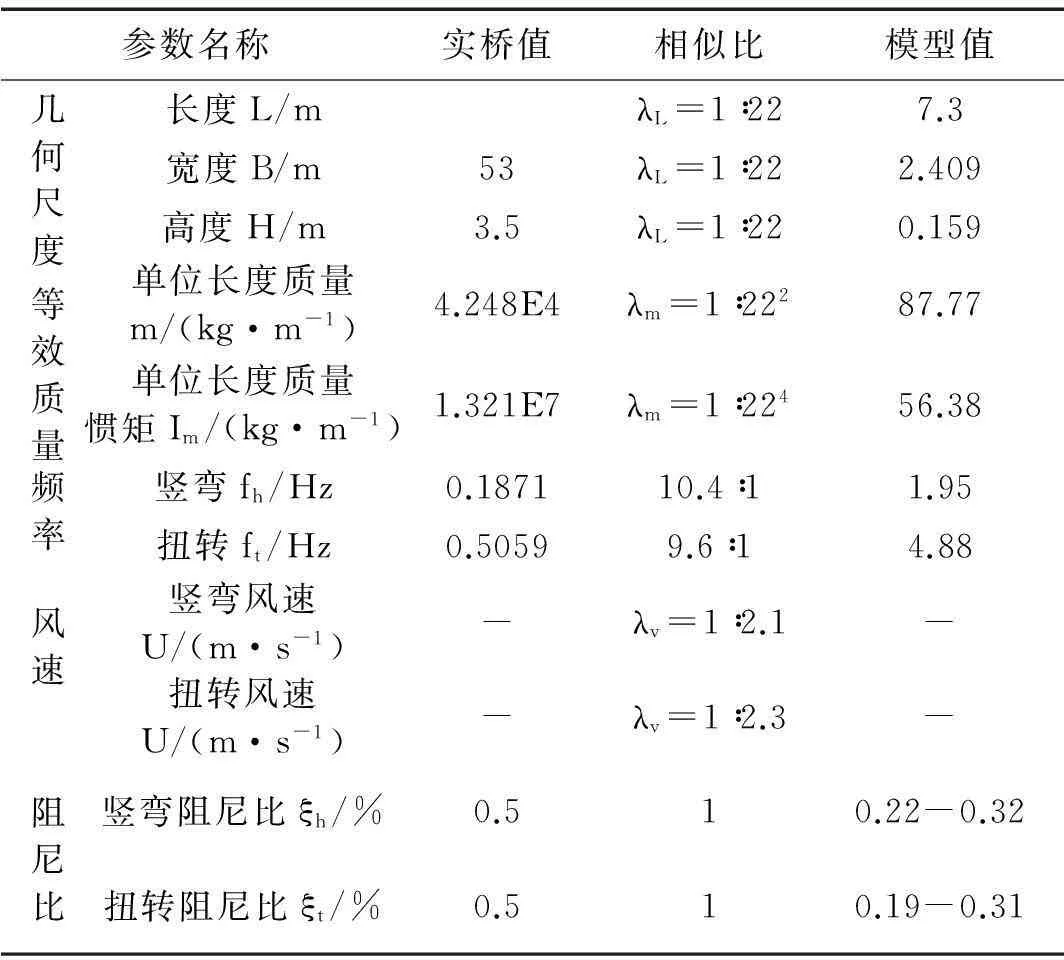
表1 大比例节段模型试验主要参数
试验模型采用两根工字钢芯棒,用5道工字钢横梁焊接形成骨架,保证模型有足够的刚度不发生局部变形,并外覆3 mm航空板以模拟桥梁的气动外形。桥面护栏及检修车轨道等附属结构采用有机玻璃雕刻而成。刚体模型由8根弹簧弹性悬挂于洞壁中支架上,通过调节整个系统质量及质量惯矩并配以适当刚度、间距弹簧准确模拟对应实桥的一阶竖弯、扭转运动质量—刚度系统。据节段模型设计相似性要求及模型与实桥频率比确定试验风速比,获得实桥主要参数与节段模型主要参数间对应关系,见表1。位移信号用日本Matsushita公司MLS LM10-130 ANR1215型激光位移传感器测量,试验共安装4个激光位移传感器,分别对称布置于两根吊臂的4个测点(图3)。
1.3试验结果
原型断面成桥状态3°、0°及-3°攻角三种工况均在均匀流场中进行,见图4。原型断面竖弯及扭转涡振响应见图5。由图5看出,在风攻角3°、0°及-3°工况下,主梁原型断面均出现明显的竖弯及扭转涡振现象。其中3°风攻角工况的竖向涡振风速锁定区间为2~3 m/s,最大竖向涡振振幅约达18 mm;扭转涡振区间共两个,第一个为5.9~6.4 m/s,最大扭转涡振振幅约达0.06°,第二个为12~13.4 m/s,最大扭转涡振振幅约达0.25°。在0°攻角工况下,竖向涡振风速锁定区间为2~3 m/s,最大竖向涡振振幅约达15 mm,无扭转涡振。 在-3°攻角工况下,竖向涡振风速锁定区间为1.8~2.8 m/s,最大竖向涡振振幅约达12 mm;扭转涡振风速锁定区间为5.2~5.8 m/s,最大涡振振幅约达0.07°。

图4 风洞中大比例节段模型 Fig.4 Large-scale sectional model in the wind tunnel
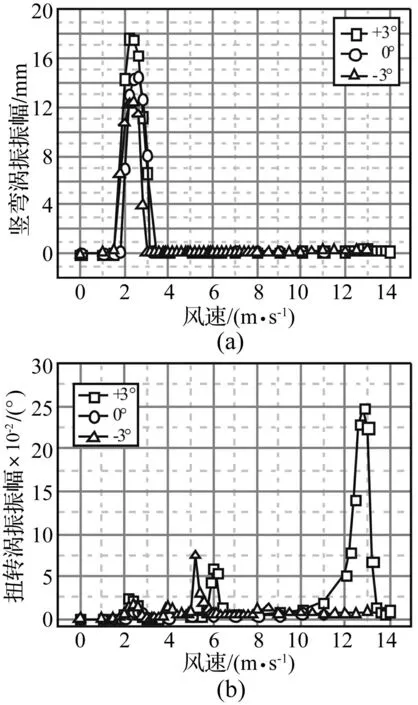
图5 原型断面竖弯及扭转涡振响应 Fig.5 The responses of vertical and torsional VIV
为寻找涡振发生原因,在3°攻角下利用三种措施进行风洞试验。措施1:去除主梁底板外侧检修车轨道,见图6(a);措施2:去除主梁底板内侧检修车轨道,见图6(b);措施3:去除主梁底板内、外侧检修车轨道,见图6(c)。
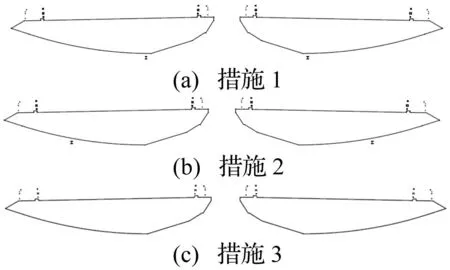
图6 针对检修轨道布置的三种措施方案 Fig.6 Three arrangements of maintenance rails
风洞试验结果显示,用措施1并不能消减竖弯及扭转涡激共振振幅;用措施2、3时竖弯及扭转涡振现象均消失,见图7。由试验结果可初步确定,该主梁断面涡振现象由内侧检修车轨道所致,而实际桥梁需要检修车轨道不能去除,因此须找到对内侧检修车轨道的优化方案。
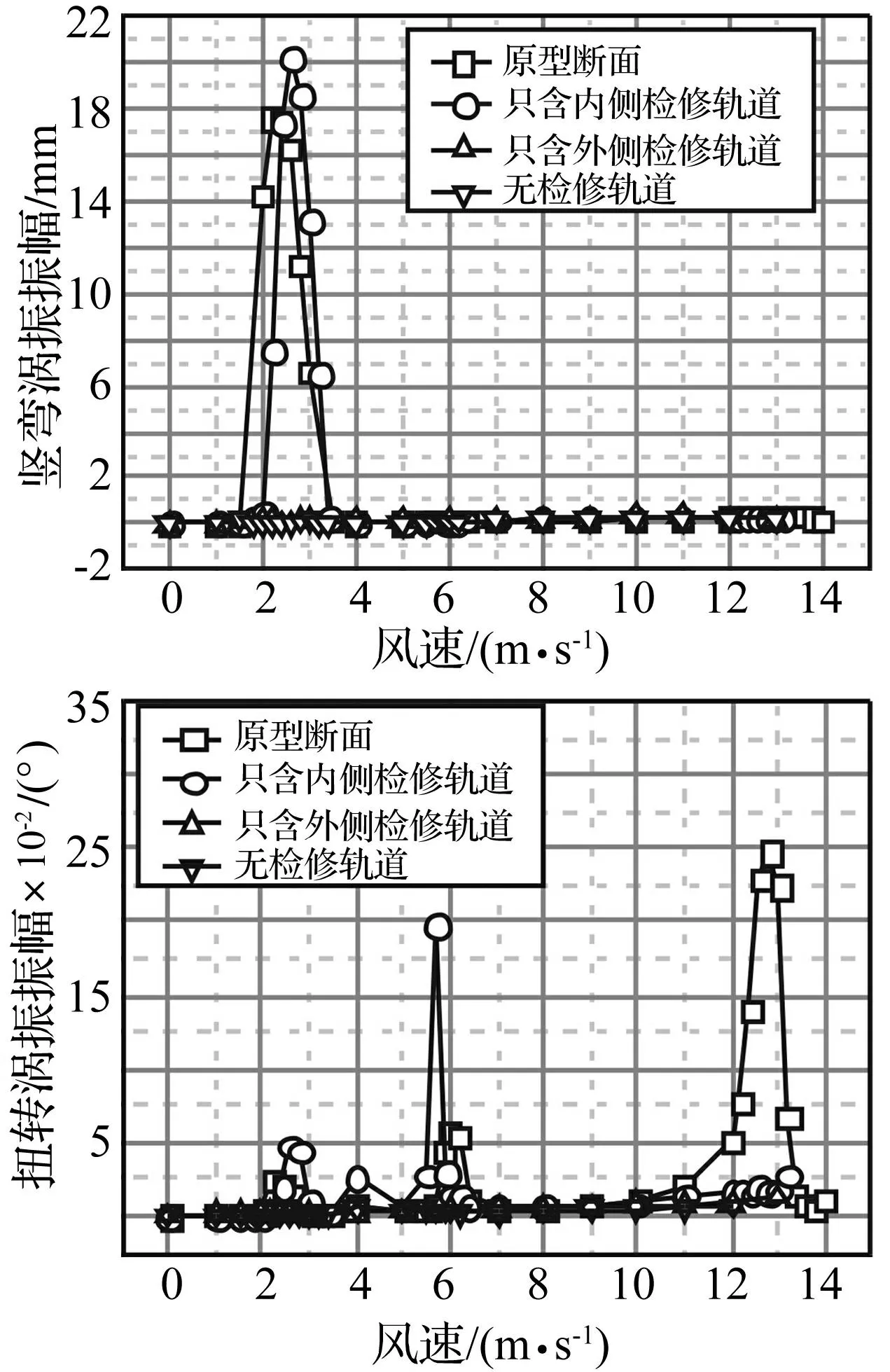
图7 竖弯及扭转涡振响应对比结果(α=3°) Fig.7 Comparison results of vertical and torsional VIV (α=3°)
2涡振产生原因及对策
2.1主梁断面绕流流场形态
本文采用主梁断面周围绕流流态特征理解涡振发生原因。用ANSYS的FLUENT有限体积法求解器进行数值计算。
几何计算域设置见图8,其与风洞试验类似,入口为均匀流,出口为固定压力,其它运输量的梯度变化为零,上下为对称性边界,主梁壁面为无滑移边界条件。计算域为124D×56D,其中D为主梁断面高度。在主梁壁面10D×3D附近局部加密,见图9。该种设置旨在保证结果可靠性情况下提高计算效率。
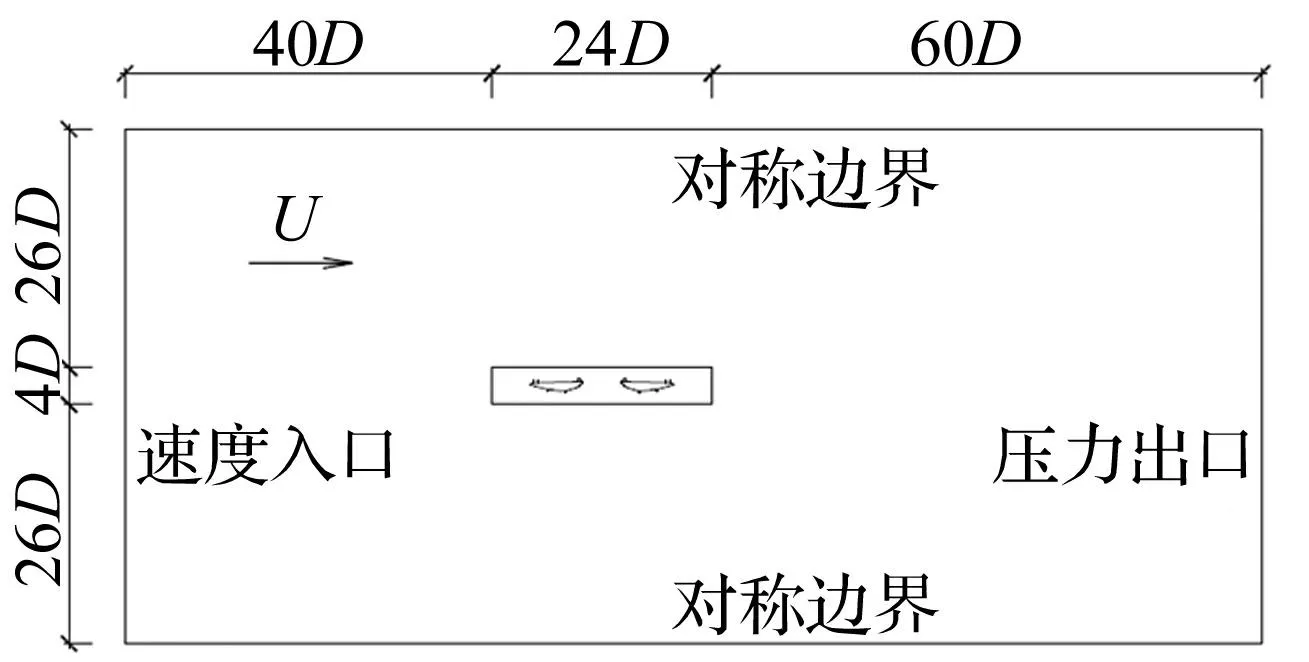
图8 计算域划分及边界条件处理 Fig.8 Overview of computational domain and boundary conditions

图9 计算域网格划分 Fig.9 Mesh of the computational domain
FLUENT求解器中计算参数见表2,其中雷诺数Re设为28300(针对梁高定义),与大比例节段模型试验竖弯涡振区雷诺数保持一致。雷诺数计算式为
(1)
式中:ρ=1.225 kg/m3为空气密度;v=2.6 m/s为来流风速;D=3.5/22=0.159 m为特征宽度;μ=1.789 4E-5m2/s为空气粘度系数。

表2 计算方法及参数列表
α=0°、α=+3°、α=-3°风攻角下原型断面及去掉检修车轨道断面周围速度场见图10、图11。由图10看出,三个攻角下,原型断面开槽区域均存在连续的旋涡脱落现象; 流过上游断面底板的气流遭遇内侧检修车轨道阻挡,因而加大上游断面尾流死水区宽度;由于速度梯度作用,开槽区域产生强烈且连续的旋涡脱落现象,主导主梁断面涡振发生。由图11看出,去除检修车轨道后绕流流场上游断面流过梁底的高速气流在转角处逆压梯度较小,气流在该区域分离基本未分离(类似流线型机翼),沿结构外形向上流动,使上甲板尾流形成较大死水区面积急剧减小,开槽区域连续旋涡脱落现象消失。
三种风攻角下风轴阻力系数Cd对比结果见图12。
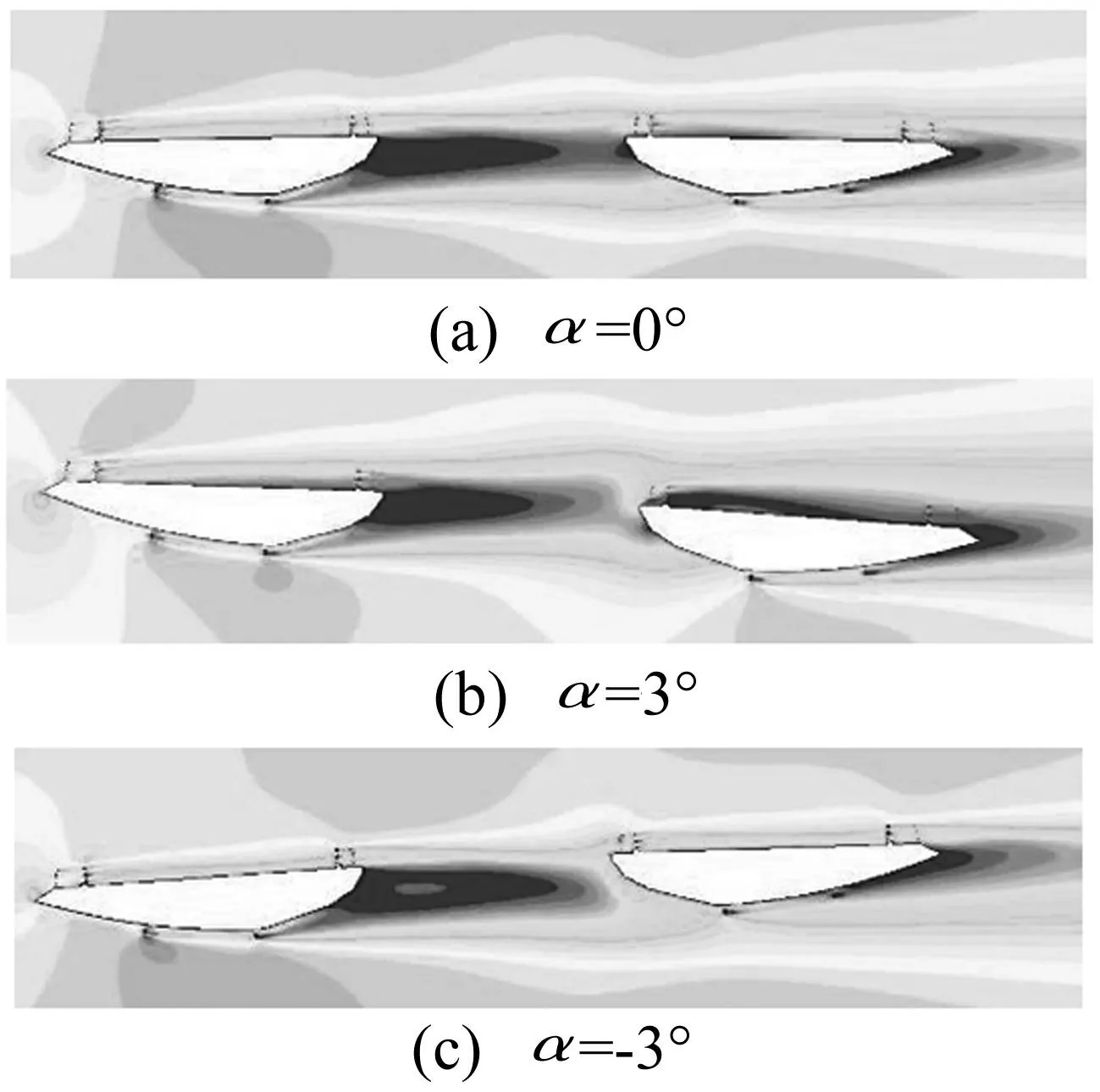
图10 原型断面速度场图 Fig.10 Velocity field around original section
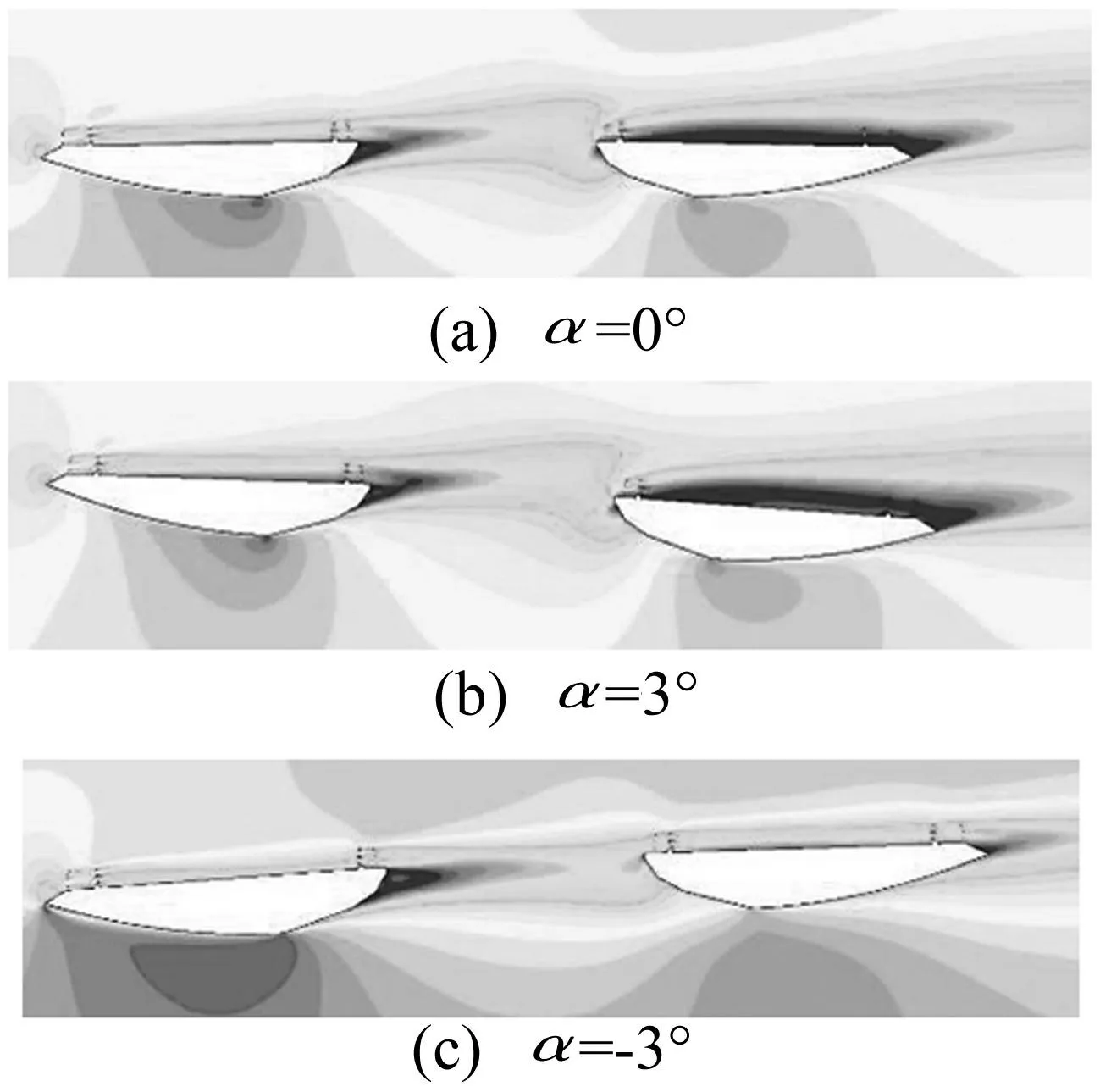
图11 去掉检修车轨道断面速度场图 Fig.10 Velocity field around section without maintenance rails
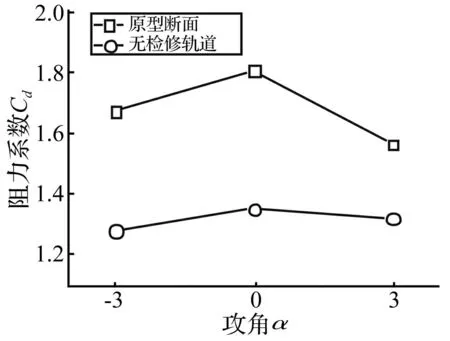
图12 三风攻角下风轴阻力系数C d对比结果 Fig.12 Comparison results of C d under three angles of wind incidence
2.2抑制涡振的气动措施
为尽量减小内侧检修车轨道的阻挡作用,提出抑振措施,即将内侧检修车轨道向主梁中心线平移一定距离(内侧斜腹板中点下方,与原位置相距100 mm),远离梁底转角敏感位置,见图13。
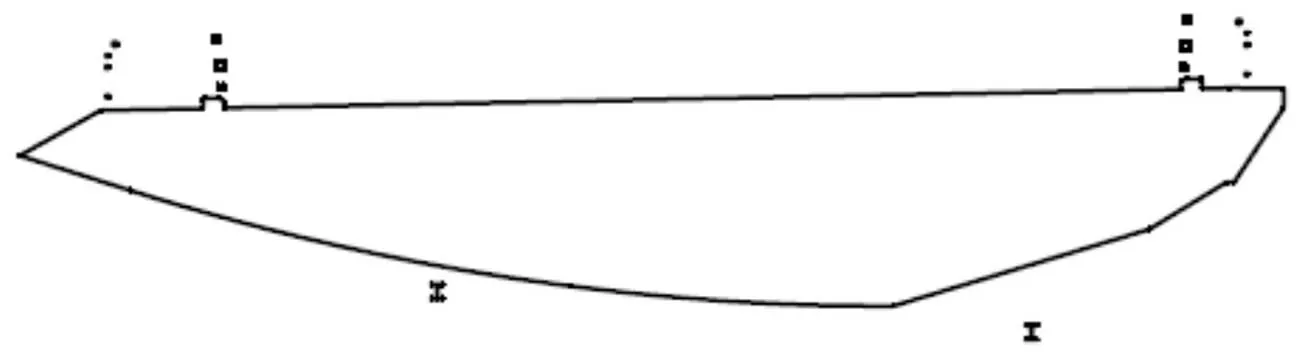
图13 改进断面示意图 Fig.13 Sketch of modified section
改进断面在三个风攻角下的周围速度场见图14。由图14看出,内侧检修车轨道向主梁中心线移动一定距离后,上游断面流过梁底的高速气流在转角处不受内侧检修车轨道影响,气流在该区域分离较小,沿结构外形向上流动,使上甲板尾流形成的较大死水区面积减小,连续旋涡脱落现象消失。
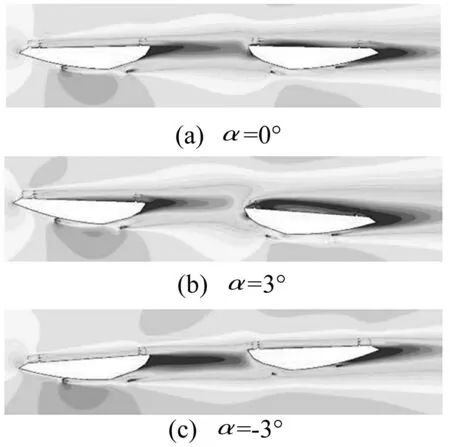
图14 改进断面速度场图 Fig.14 Velocity field around modified section
3表面静态压力测量
为更好揭示三种气动措施抑制涡振机理,试验中通过固定节段模型的弹簧系统,令节段模型保持静止不动,测量3°攻角时原型断面最大涡振振幅对应的风速2.6 m/s下节段模型表面压力分布。在7.3 m节段模型上近跨中一开槽段中间位置(图3)布置一排测压点。每排测压点布置见图15,在分离的两梁体对称、均匀布置77个同步测量压力点。
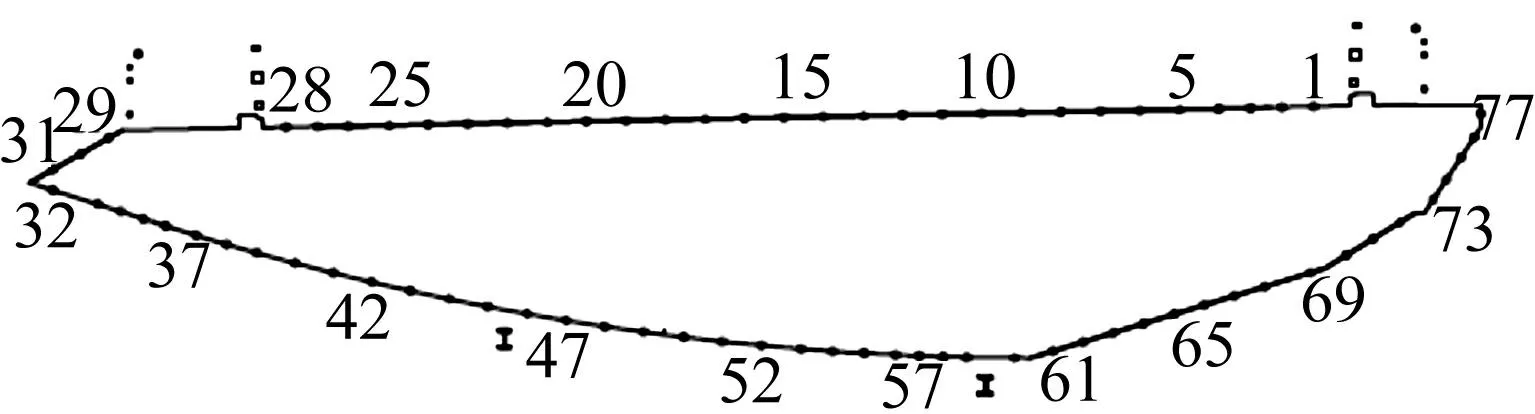
图15 横断面测压点位置示意图 Fig.15 Layout of the pressure taps
表面压力测量用美国Pressure System Inc扫描阀公司的ESP-64HD型电子压力扫描阀与DTC Initium处理器。本试验用1个DTC Initium处理器与4个ESP压力扫描阀模块,计256个测点。采样频率300 Hz,采样时长60 s。
3.1平均压力系数分布
浸没在流体中的钝体表面会受流体压力作用,钝体表面压力分布会随外形不同而不同。由平均压力分布状况可判断气流在主梁断面的分离及再附情况。
本文采用无量纲压力系数表征表面压力分布规律。压力系数定义为局部风压与来流动压之比,即
(2)
式中:p为某点处局部风压;ps为扫描阀静压;pd为来流动压;pt为扫描阀总压。当p分别为一个时间样本下平均风压与脉动风压时,其压力系数即为平均压力系数与脉动压力系数。
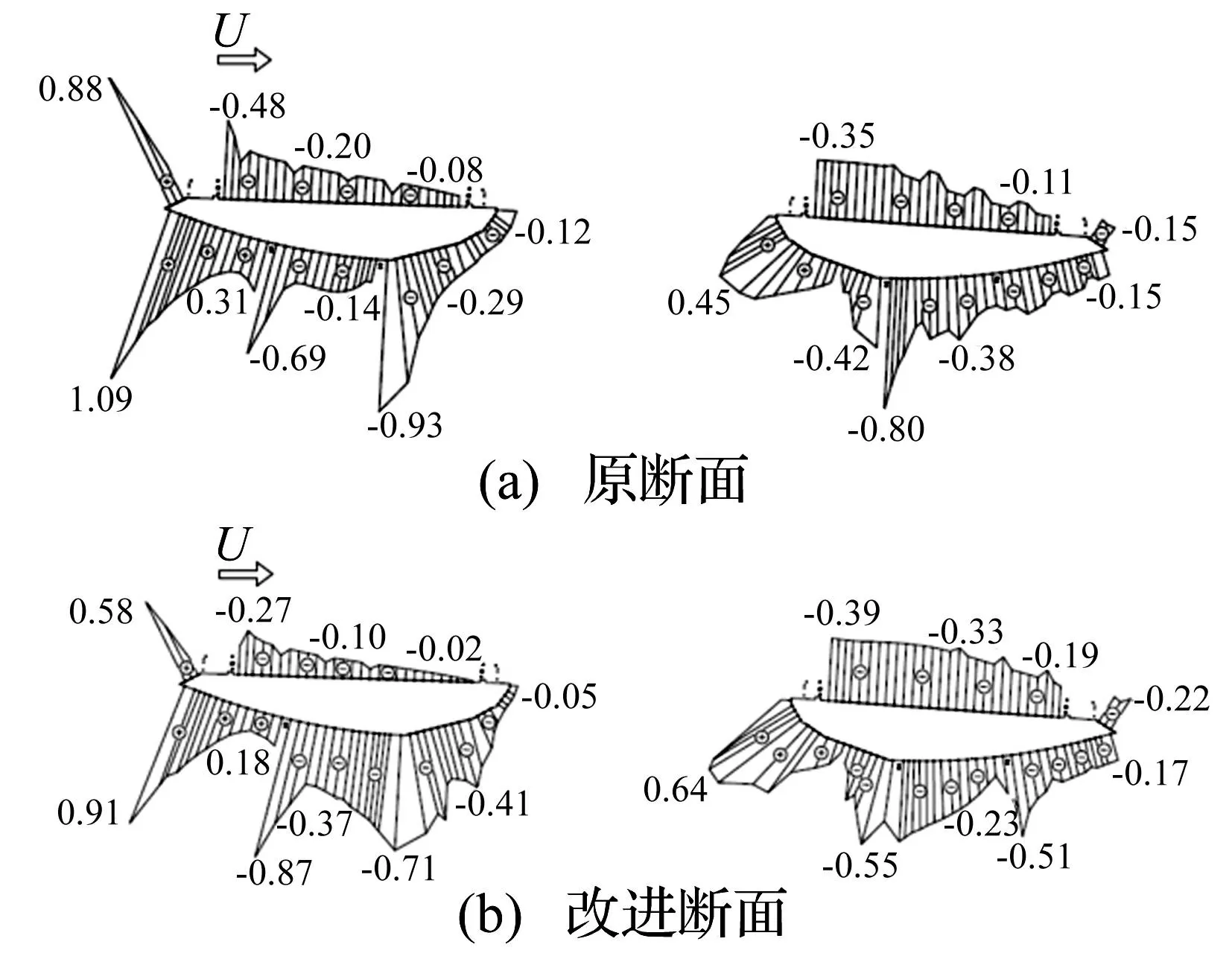
图16 平均压力系数分布对比图(α=3°) Fig.16 Comparison of mean pressure coefficients (α=3°)
原型断面与改进断面在3°攻角时主梁表面平均压力系数分布见图16,并在特征位置标注压力系数数值。由图16看出,①上游断面迎风侧风嘴上下斜腹板的压力均为正压,表现出由风嘴前缘向后迅速衰减趋势;流向上甲板的气流遭遇防撞栏阻挡产生分离,分离区旋涡使上甲板受吸力作用(负压),且负压绝对值呈由上游向下游衰减趋势;而在上游断面底板上,气流流经检修车轨道后在其下游附近局部区域产生死水区,导致检修车轨道下游局部位置处突变产生较大负压值后向下游减小,直至再次遭遇检修车轨道阻挡,产生强烈的流动分离,负压值突增,向下游减小;上游断面整个内侧斜腹板为尾流区域,即旋涡聚集地,故作用于此的平均压力均为负压。②与上游断面平均压力分布规律一致,气流除在下游断面迎风侧斜腹板处产生正压,其余区域(包括流动分离区、尾流区)均为负压作用区,且气流遭遇检修轨道会产生负压绝对值突增。③改进断面与原型断面的平均压力系数分布不同之处在于,因内侧检修车轨道向主梁中心线偏移一段距离,气流沿梁体外形平稳过渡,无明显的流动分离现象。故上游断面底板内侧转角处负压值无有产生剧烈突变,向下游平稳减小。下游断面亦同。
3.2脉动压力系数分布
气流流经浸没的钝体时会在钝体表面棱角处产生流动分离形成旋涡,且随气流向下游运动过程中可能再附在钝体下游表面形成再附,而旋涡分离、再附必会产生作用于钝体表面的脉动压力。
原型断面及改进断面在3°攻角时主梁表面脉动压力系数分布见图17,并在特征位置标注压力系数数值。由图17看出,① 3°风攻角时作用于下游断面的脉动压力系数值明显大于上游断面,此因下游断面整体浸没在上游断面产生的紊流中,造成下游断面产生的整体脉动压力能量大于上游断面。②脉动压力沿上下游断面各自表面分布呈一定特征。下游断面整个桥面板区域由于栏杆阻挡处于强烈的气流分离与再附区使脉动压力非常显著,且越往下游脉动压力系数值越小;近开槽区域内侧斜腹板由于受上游来的旋涡脱落作用力,压力脉动强烈;在内侧检修车轨道局部位置,由于受该轨道阻挡使流动分离十分强烈在局部产生较大脉动压力。对上游断面,除在上甲板区域、检修车轨道位置及箱梁棱角处受较大脉动压力,其余断面所受脉动压力较均匀。③将检修车轨道向主梁中心线偏移后流经梁底的高速气流在底板内侧转角处无阻挡,可继续沿梁体外形向上流动,移动后的检修车轨道距上游断面较远阻挡效应大大减小。此时整个开槽区域只剩因桥面板棱角造成的流动分离及再附,因而脉动压力大大减小。
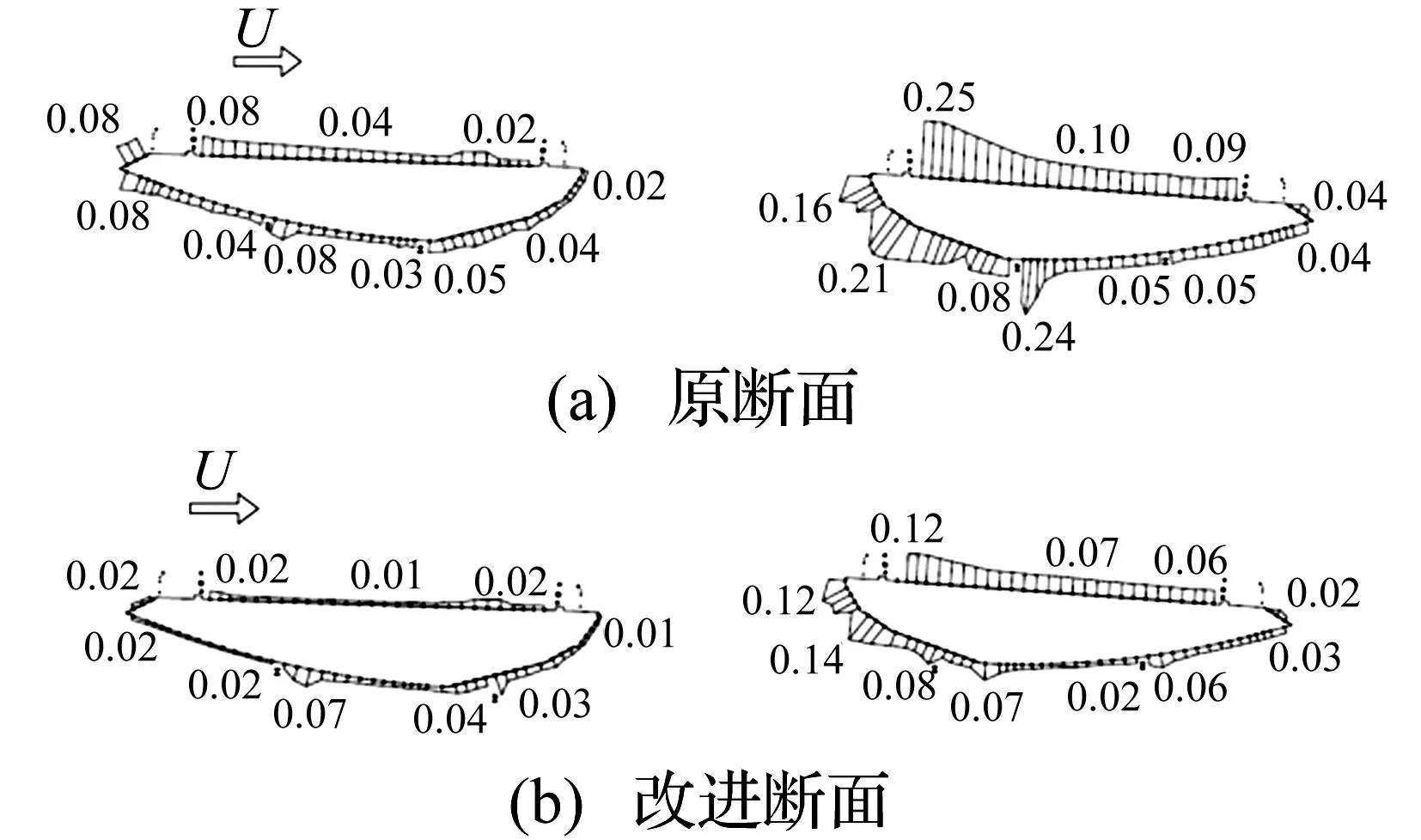
图17 脉动压力系数分布对比图(α=3°) Fig.17 Comparison of fluctuating pressure coefficients (α=3°)
3.3特征测点脉动压力功率谱
在3°风攻角下选主梁上下游两断面的两特征测点进行压力功率谱分析,见图18。71#测点位于两主梁断面近开槽区域内侧斜腹板中间,即涡结构聚集地中两特征点。

图18 用于功率谱分析的特征测点 Fig.18 Midpoint of upwind and downwind inward inclined panels used for pressure PSD analysis
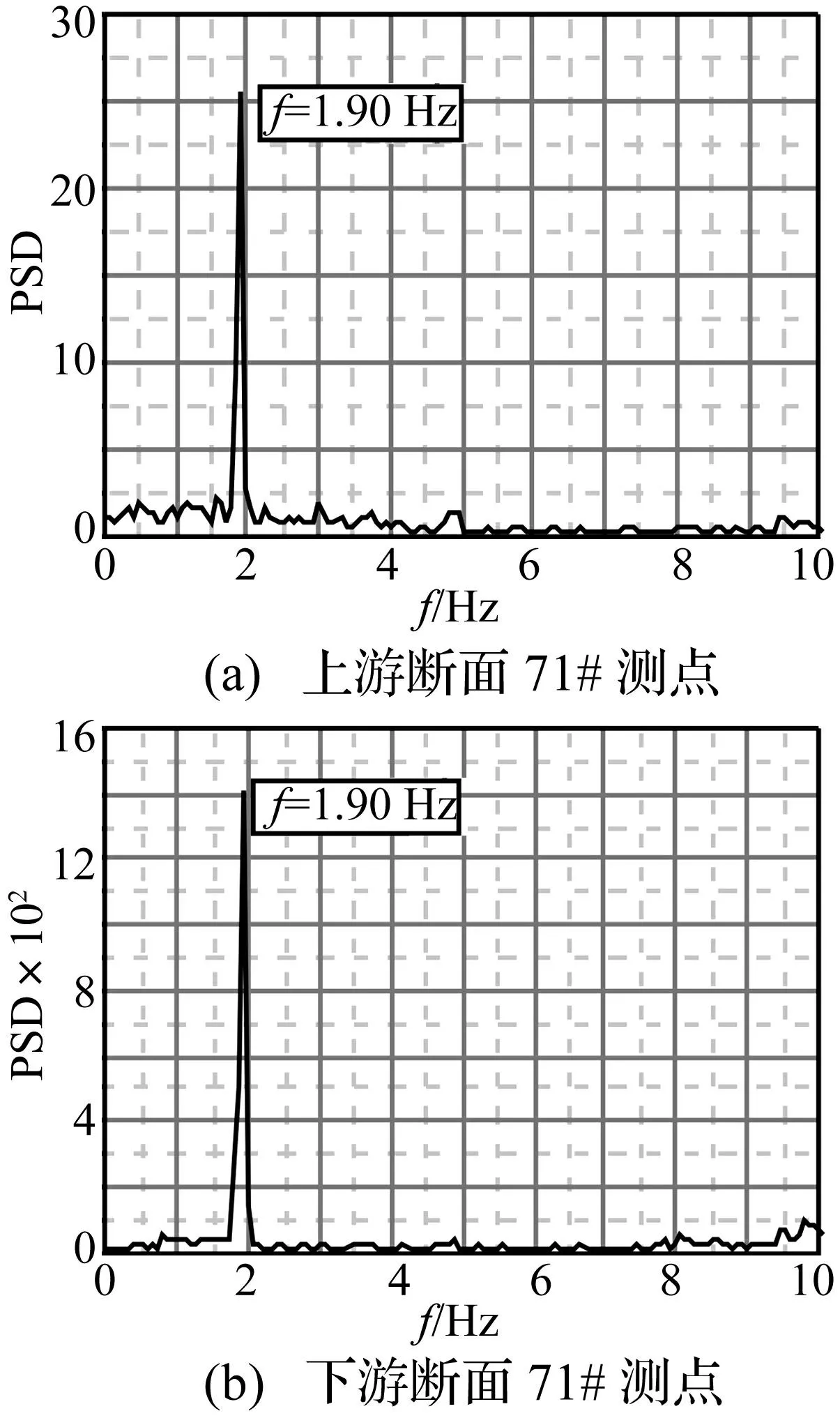
图19 原型断面特征测点压力功率谱图 Fig.19 Pressure PSD on point 71 of original section
原型断面与改进断面特征测点压力脉动的功率谱见图19、图20。由图19看出,原型断面静止时上下游71#特征测点压力脉动的卓越频率均为1.90 Hz(接近主梁竖弯涡振频率),说明2.6 m/s风速下,作用于结构的强迫力频率恰与其自身频率吻合,从而引起涡激共振。下游断面71#测点的脉动压力在1.90 Hz的能量远高于上游断面特征测点,说明在上游断面内侧斜
腹板处形成的旋涡在向下游流动过程中不断发展扩大,在下游内侧斜腹板上脱落,对下游内侧斜腹板造成巨大冲击作用,作用力远大于上游断面。由图20看出,采用改进断面后因内侧检修车轨道偏离,流经梁底的高速气流无阻挡顺利向上流动,对原开槽区域产生的规律旋涡区产生冲击作用,打碎原规律旋涡,破坏上下游内侧斜腹板上各点压力脉动的周期性,表现在特征测点压力脉动的卓越频率较分散,无相同值,从而能成功抑制涡振的产生。
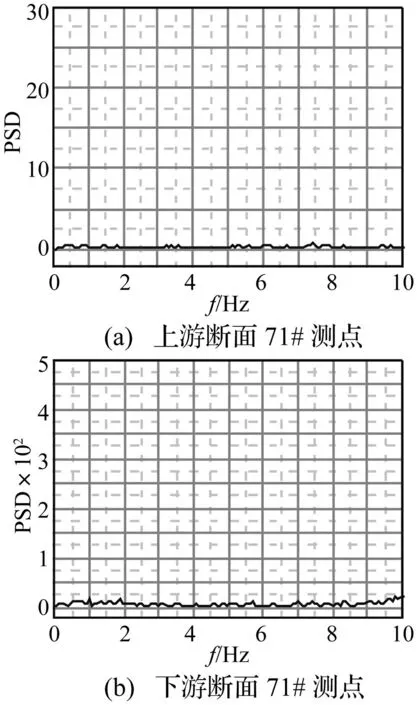
图20 改进断面特征测点压力功率谱图 Fig.20 Pressure PSD on point 71 of modified section
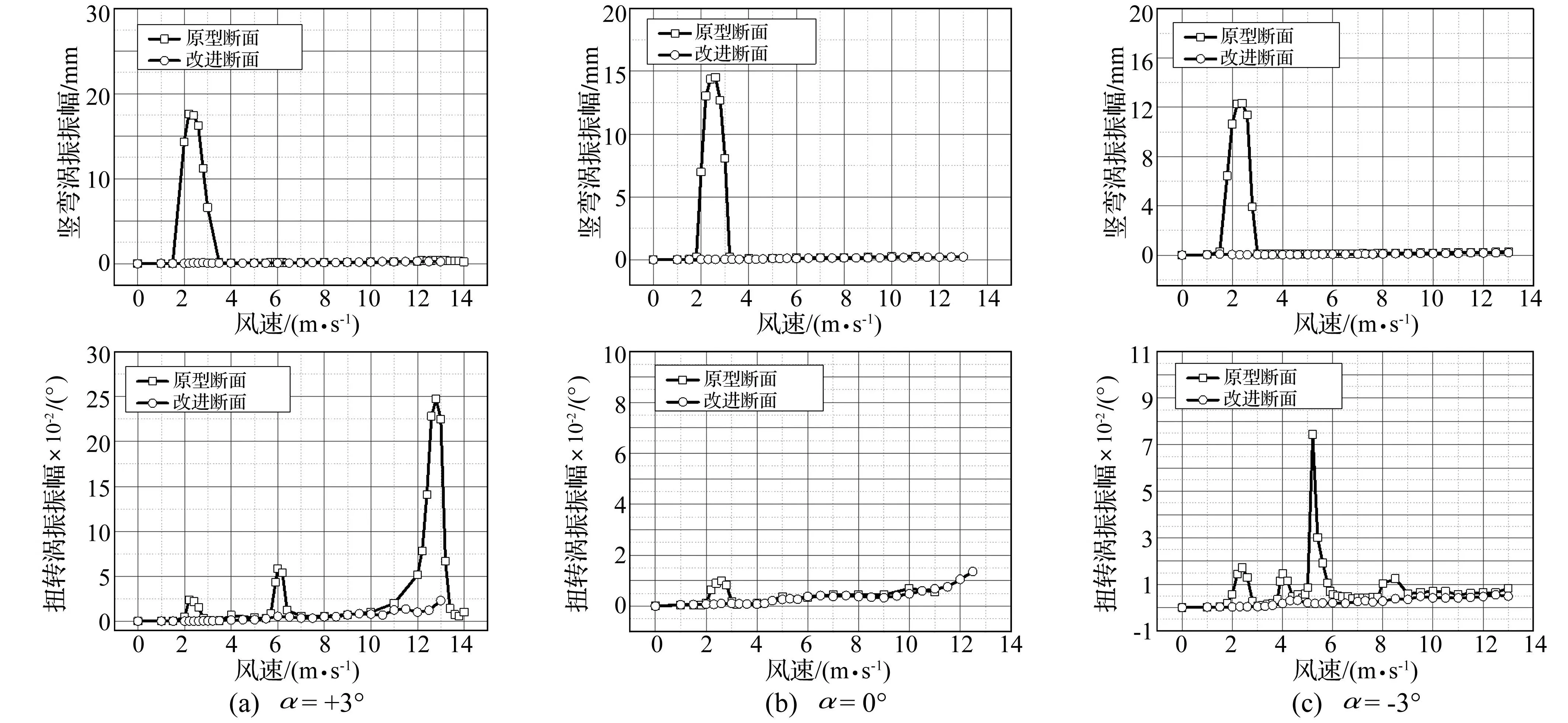
图21 改进断面试验结果 Fig.21 Test results of modified section
4抑振措施试验结果
针对气动措施进行大比例节段模型涡振试验,并与原型断面结果对比,见图21,图中未发现明显的竖向、扭转涡振现象。由此看出,所提改进断面可有效抑制涡振。与通过CFD计算所得流场形态特征及通过测压试验所得平均压力分布、脉动压力分布、脉动压力功率谱结果规律一致。
5结论
本文基于大比例节段模型风洞测振、测压试验及计算流体力学CFD方法进行中央开槽箱梁涡激共振特性及抑振措施机理研究,结论如下:
(1)由风洞试验结果显示,位于气动敏感位置的内侧检修车轨道是诱发涡激共振原因。
(2)CFD数值模拟表明,流经上游断面底板的气流遭遇内侧检修车轨道阻挡时会加大上游断面尾流死水区宽度,因速度梯度作用开槽区域产生强烈且连续的旋涡脱落现象,主导主梁断面涡振发生。
(3)本文内侧检修车轨道向主梁中心线偏移一定距离方案,可使上游断面流经梁底的高速气流在底板内侧转角处不受该轨道影响,气流分离点延后,开槽区域连续旋涡脱落现象消失。
(4)通过主梁断面表面静态测压试验知,用本文方案可使气流沿梁体外形平稳过渡,不会产生明显的流动分离现象,上游断面底板内侧转角处负压值不会产生剧烈突变。且上、下游断面整个内腹板的脉动压力减小、能量分散,无一致的卓越频率。
(5)通过对改进断面进行大比例节段模型涡振风洞试验知,原有竖弯涡振与扭转涡振现象消失,表明该抑振措施有效。
参考文献
[1]Larose G L, Larsen S V, Larsen A, et al. Sectional model experiments at high reynolds number for the deck of a 1018m span cable-stayed bridge[C].//Proceedings of 11thInternational Conference on Wind Engineering,USA: Lubbock, TX, 2003:373-380.
[2]Matsuda K, Cooper K R, Tanaka H, et al. An investigation of reynolds number effects on the steady and unsteady aerodynamic forces on a 1:10 scale bridge deck section model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011(89):619-632.
[3]李玲瑶,葛耀君.大跨度桥梁中央开槽断面的涡振控制试验[J]. 华中科技大学学报(自然科学版),2008,36(12):112-115.
LI Ling-yao, GE Yao-jun. Experiments of vortex control for central-slotting on long-span bridge[J]. Journal of Huazhong University of Science and Technology (Nature Science), 2008, 36(12): 112-115.
[4]欧阳克俭,陈政清,韩艳,等. 桥面中央开口悬索桥涡激共振与制涡试验研究[J]. 振动与冲击, 2009, 28(7):199-202.
OUYANG Ke-jian, CHEN Zheng-qing, HAN Yan,et al. Vortex-induced resonance of a suspension bridge with central-slotted deck and its control test study.[J]. Journal of Vibration and Shock, 2009, 28(7):199-202.
[5]廖海黎,王骑,李明水. 嘉绍大桥分体式钢箱梁涡激振动特性风洞试验研究[C].//第十四届全国结构风工程学术会议论文集[A]. 北京: 中国土木工程学会, 2009:580-584.
[6]汪正华,杨詠昕,葛耀君. 分体式钢箱梁涡激振动控制试验[J]. 沈阳建筑大学学报(自然科学版),2010,26(3):433-438.
WANG Zheng-hua, YANG Yong-xin, GE Yao-jun. Investigation on the vortex-induced vibration of a twin box bridge section[J]. Journal of Shenyang Jianzhu University (Natural Science), 2010,26(3):433-438.
[7]孟晓亮,郭震山,丁泉顺,等. 风嘴角度对封闭和半封闭箱梁涡振及颤振性能的影响[J]. 工程力学, 2011 (A01):184-188.
MENG Xiao-liang, GUO Zhen-shan, DING Quan-shun, et al. Influence of wind fairing angle on vortex-induced vibrations and flutter performances of closed and semi-closed box decks[J]. Engineering Mechanics, 2011 (A01):184-188.
[8]王骑,林道锦,廖海黎,等. 分体式钢箱梁涡激振动特性及制振措施风洞试验研究[J]. 公路,2013(7):294-299.
WANG Qi, LIN Dao-jin, LIAO Hai-li,et al. Investigation on the vortex-induced vibration and aerodynamic countermeasures of twin box bridge by wind tunnel tests[J]. Highway, 2013(7): 294-299.
[9]Larson A, Savage M, Lafrenière A,et al. Investigation of vortex response of a twin box bridge section at high and low reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008(96):934-944.
[10]Li Hui, Shujin Laima, Ou Jin-ping, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J]. Engineering Structures, 2011(33):1894-1907.
[11]Kwok K C S, Qin X R, Fok C H,et al. Wind-induced pressures around a sectional twin-deck bridge model: effects of gap-width on the aerodynamic forces and vortex shedding mechanisms[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012(110):50-61.
[12]Watanabe S, Fumoto K. Aerodynamic study of slotted box girder using computational fluid dynamics[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008(96): 1885-1894.
[13]Laima Shujin, Li hui, Chen Wen-li,et al. Investigation and control of vortex-induced vibration of twin box girders[J]. Journal of Fluids and Structures, 2013, 39:205-221.
[14]何晗欣,李加武,周建龙. 中央开槽箱形断面斜拉桥的涡激振动试验与分析[J]. 桥梁建设,2012,42(2):34-40.
HE Han-xin, LI Jia-wu, ZHOU Jian-long. Testing andanalysis of vortex-excited vibration of central slotted box section cable-stayed bridge[J]. Bridge Construction, 2012,42 (2) :34-40.


