基于EEMD和能量法的谐振接地配网故障选线方法

褚福亮，金涛

(福州大学电气工程与自动化学院，福建福州 350116)

0 引言

随着城市的发展和电力系统容量的不断增加，当配网发生单相短路故障时，故障电流也较以前大很多倍，严重时系统中会产生弧光过电压，其值为相电压的2．5～3倍，严重威胁着系统的绝缘，而且极易使故障范围扩大．为了限制短路点电流的大小，防止上述危害的发生，配电网广泛采用中性点谐振接地运行方式．适用于此类配电网的故障线路的选择方法主要有小波分析法、首半波法、能量法、注入信号跟踪法、拉路法、谐波分量法、人工智能法等．其中对于小波分析法，选线准确度较高［1－2］，但是小波变换的分解结果由预先确定的基函数所决定，因而小波变换不能够根据信号的特征进行自适应分解;首半波法易受过渡电阻的影响而引起误判;注入信号跟踪法也易受过渡电阻的影响，当过渡电阻较大时，信号非常微弱，同时注入的信号易受干扰;拉路法虽已改进，但仍需要人工操作，判别故障的时间仍较长．EEMD能根据信号本身的特点对信号进行分解．EEMD适用于分析瞬时出现的信号，利用EEMD可把任何信号分解成若干个固有模态函数(IMF)分量和一个剩余分量r．也就是说，原始信号中不同频率的交流分量被分解成不同尺度的固有模态函数IMF，直流分量被包含在剩余分量中．

在中性点经消弧线圈接地的配电网中，若某一出线发生单相短路故障，则暂态过程中，感性电流的频率主要集中在0～50 Hz，而容性电流的频率为300～3 000 Hz，由于频率相差很大，二者不能相互抵消，又由于所有健全相的电容电流都通过接地点流入故障线路的故障相中，因而故障线路比健全线路含有的高频分量丰富．本研究首先取故障起始时刻附近的各线路零序电流进行EEMD分解，再取出各电流的较高频率的分量和剩余分量，然后分别求取各线路的频率较高分量和剩余分量的能量和，再求出各线路的能量权重系数，通过分析比较能量权重系数的大小可以确定出故障元件，该方法不易受过渡电阻的影响，抗干扰能力强，判别故障时无需人工操作．通过编程和Matlab/Simulink仿真，验证了该方法在不同单相短路故障情况下都能可靠、准确地判别出哪一条出线或母线发生了故障．

1 暂态特征分析

图1描述了暂态电流的流通路径，设配电网有2条出线，在线路L2上发生A相短路故障，由于L1、L2的A相电压突然下降，使得L1、L2的A相对地电容储能迅速被释放，放电电流以表示;而B相、C相的电压突然升高，使得B相、C相的对地电容迅速充电，充电电流以→表示;暂态电感性电流以表示．其中放电电流的流通路径:从L1、L2的A相对地电容开始，经过故障点，有一电流直接回到L2的A相对地电容．另一电流经L2的A相线路和母线后，流回L1的A相对地电容中;而充电电流的流通路径:从L1、L2的B相和C相对地电容开始，经故障点、故障点所在的支路和电源后流回L1、L2的B相和C相对地电容中．

可知，频率较高的容性电流包含在故障点的电流ik中，同时感性电流也包含在内，其表达式为:

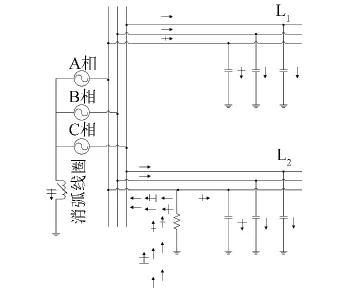
图1 暂态电流分布图Fig．1 Distribution of transient current

式中:ik．s、ik．t为稳态分量和暂态分量;ICm为故障点流过的容性电流的幅值;ILm为故障点流过的感性电流的幅值;φ为故障瞬间的电压相角;τL、τC为时间常数．

当故障过渡到稳定状态时，故障线路故障相的电流只含有工频分量，其特性随着补偿度的不同而不同，对于稳定状态时的电流来说，可以通过图2看出故障线路与健全线路两者的电流相位几乎相同，大小也相差不大;在过渡到稳定状态的过程中，接地点的电流包含频率较高的容性电流和衰减的直流感性电流，而且当φ=π/2时发生故障，暂态电流主要为容性电流，当在φ=0时发生故障，暂态电流主要为感性电流．由图3可见两者的特征有明显差异．

从故障发生到稳定状态的过渡过程中零序电流的分布规律为:

1)当某一出线发生故障时，该条线路将流经全系统健全线路的频率较高的容性电流和消弧线圈产生的衰减性感性电流，由于感性电流频率主要集中在0～50 Hz，容性电流的频率主要集中在300～3 000 Hz，因此二者不能相互补偿;而非故障线路中只流经本身的对地电容的充、放电电流．

2)当母线发生故障时，暂态过程中所有出线只流经自身的暂态容性电流，其大小相差不大．

图2 稳态时的零序电流Fig．2 The zero sequence current of steady state

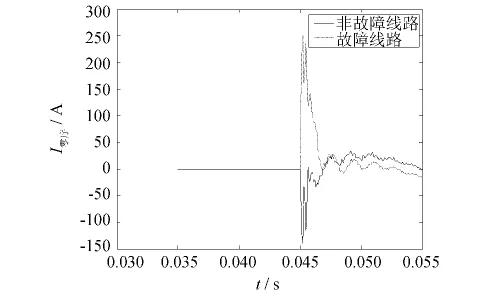
图3 暂态时的零序电流Fig．3 The zero sequence current of transient state

2 EEMD原理

1998年，美籍华人黄锷(Norden E．Huang)［3］提出了希尔伯特 －黄算法(Hilbert－Huang transform，HHT)．该算法能将复杂信号分解成一组频率不相同的分量即IMF，它无需选择基函数，而是根据信号的特性依次剥离各个模态［3－6］．

2．1 固有模态函数

N E Huang提出IMF必须满足如下两个条件:第一，在IMF的整个数据列中，所有极大值点和极小值点的总数应与零点的个数相等，或者相差一个;第二，必须符合下面的等式条件:

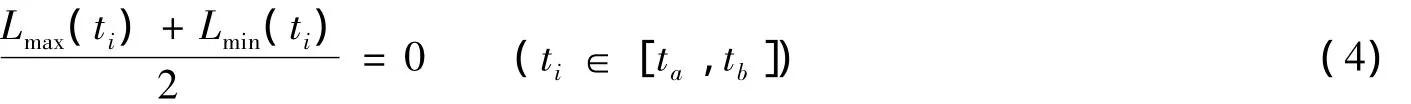
式中:Lmax(ti)、Lmin(ti)为上、下包络线的数学表达式．

2．2 EMD 原理

对于一个原始时间序列x(t)，其EMD分解步骤为:

1)确定原始时间序列x(t)的所有极小值点、极大值点;

2)利用所有极大值点和极小值点并采用插值法求取原始信号的上、下包络线，本算例采用三次样条插值，并计算两条包络线的均值m(t);

3)信号x(t)减去均值m(t)，可得:

4)判断h(t)是否满足IMF条件，若满足条件，则h(t)就是x(t)的一个IMF分量，接着转到第5)步．若不满足，把h(t)作为原始数据转到第1)步;

5)令c(t)=h(t)，c(t)即为IMF分量，然后作差

得到剩余分量r(t);

6)判断r(t)是否满足终止条件

式中:g(t)为单调函数或常量．若满足条件则EMD分解过程结束，不能提取的分量为剩余分量，若不满足将r(t)作为新的输入信号转到第1)步．

经以上步骤，原始时间序列x(t)被拆分成若干固有模态函数分量ci(t)和剩余分量r(t)，即:

设原始信号x(t)的表达式如下:

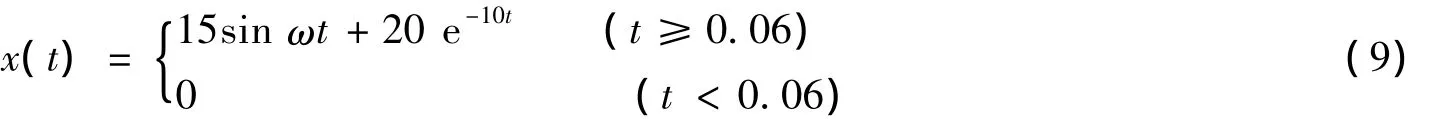
采样频率取12．8 kHz，图4展示了EMD的分解结果，可知IMF1中含有工频分量，而直流分量被包含在剩余分量r中，但EMD的结果中出现了虚假成分和频率交叠现象．对于瞬时性出现的信号．EMD的分析能力较弱，据此Huang等人在2009年提出了集合经验模态分解(ensemble empirical mode decomposition，EEMD)．

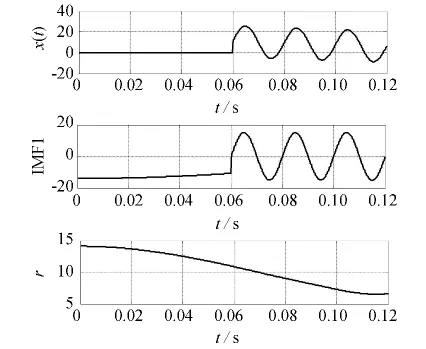
图4 EMD分解结果Fig．4 Results of EMD

2．3 集合经验模态分解

集合经验模态分解的原理为给信号叠加上均匀分布的白噪声后对信号进行经验模态分解，则不同频率的信号分量将被分解到与白噪声有关的适当频率域上．然而，每一次分解的结果中都可能会有噪声出现．但是，每进行一次分解时噪声都会不相同，当进行足够多次的经验模态分解时，然后求取相应频率的所有分量的均值，这样将会消除噪声，最后求取的均值即为分解结果．

EEMD 步骤如下［7－9］:

1)把一组白噪声信号sj(t)叠加在信号x(t)中，得:

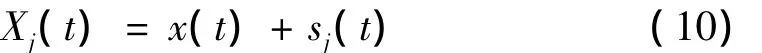
2)对Xj(t)进行EMD分解，得

式中:N为所设定的循环次数．

3)重复步骤1)和步骤2)，当重复次数满足N时转到第4)步;

4)分别求各个频率IMF分量的平均值．得到ci(t)和r(t)，可表示为:

则原始信号x(t)可表示为:

在一定的噪声幅度下，循环次数越多，最终分解得到的结果越接近真实值，但循环次数太多会延长算法的运算时间．如果加入幅度较小、信噪比较高的白噪声，EEMD分解将出现错误．

3 能量法

设谐振接地配电网有N条出现，第i条线路的尺度为j的IMF分量和剩余分量r的能量分别为:

式中:n为时间序列的长度;k为采样点;Eij为线路Li的信号在尺度j的能量;Eir为时间序列信号剩余分量的能量;m为IMF分量的个数．

线路Li的模态能量为:

所有出线的总能量为:

第i条线路的能量权重系数为:

当谐振接地配电网的某一出线发生故障时，该线路的能量权重系数与非故障线路相比大很多;当故障发生在母线上时，所有出线的能量权重系数相差无几．因此故障线路可通过比较各线路能量权重系数被选择出来．

4 接地选线方法

在分析故障时的暂态特征和能量法的选线原理的基础上，提出故障选线算法，图5为该算法的流程图．

第一步，判断系统是否发生了永久性单相接地故障，首先判断母线零序电压是否超过0．15倍的额定电压;若超过，则进行细判:判断某两相相电压是否高于额定电压，同时另一相的相电压是否低于额定电压;并且零序电流不为零［10］．若满足以上条件，则执行第二步．

第二步，读取母线零序电压，利用EEMD找出信号的突变点，然后确定故障的起始时刻［11］．

第三步，提取各线路的故障起始时刻前后各半个工频周期的零序电流，进行EEMD分解，提取各线路的高频分量和剩余分量，本文取前3个高频分量．

第四步，求各线路的能量权重系数Pi，并设定阈值Pset．若所有线路的Pi＜Pset，则母线发生了故障，若某一条线路的Pi＞Pset，则此条线路发生了故障．

图5 选线算法流程图Fig．5 Flowchart of fault line－ selection algorithm

5 仿真算例分析

为验证以上方法的正确性，利用Maltab/Simulink建立仿真模型，其示意图如图6所示，谐振接地配电网为具有6条出线的缆－线混合线路系统．其中设架空线J1为17 km，架空线J2为12 km，架空线J31为7 km，电缆线L32为9 km，电缆线L4为8 km，电缆线L51为10 km，架空线J52为8 km，电缆线L6为12 km．而线路参数如表1所示［1］．消弧线圈电感值计算公式为［1，12］:

图6 谐振接地系统模型Fig．6 The model of resonant earthed system

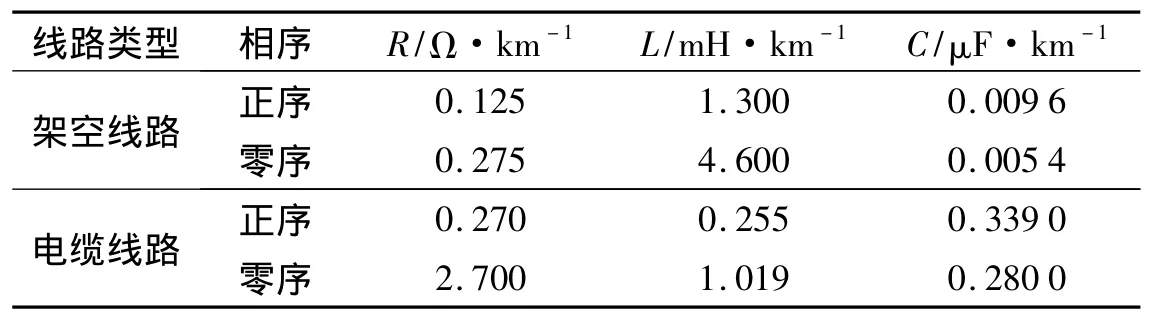
表1 线路参数Tab．1 Parameters of line

其中:

式中:lL为电缆线路总长度;lJ为架空线路总长度;CL为单位长度零序电容值;CJ为单位长度零序电感值;p为消弧线圈的补偿度，一般为5%～10%．

对消弧线圈而言，其发热损耗大约为感性损耗的2．5% ～5．0%，取3．0%［1］，可得消弧线圈的电阻值为:

整个仿真过程中采样频率均为100 kHz，所加白噪声信号的标准差为0．02，EEMD中的循环次数为100．当补偿度p为10%，即其电感值为0．275 2 H，电阻值2．594Ω时，线路4末端在相电压φ=π/2时发生单相金属性接地故障时，对于线路4的零序电流，图7展示了其波形，图8展示了通过EEMD提取出的前3个高频分量和剩余分量．

图7 线路4故障时的自身的零序电流波形Fig．7 The zero sequence current of line 4 while single phase ground fault occurring in line 4

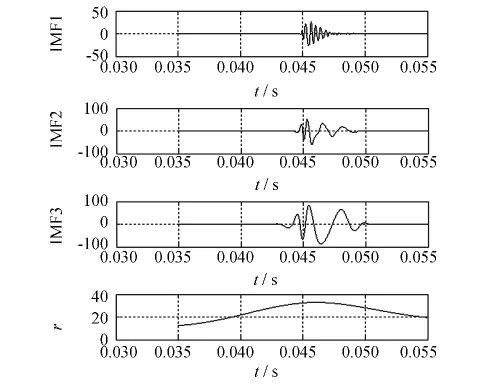
图8 EEMD分解结果Fig．8 Results of EEMD

而当相电压达到峰值，即φ=π/2时，线路1在距母线2 km处发生故障，故障点电阻为200Ω时，各线路能量权重系数如图9所示;当相电压的相角φ=π/6，母线发生故障，故障点电阻为20Ω时，各线路能量权重系数如图10所示．

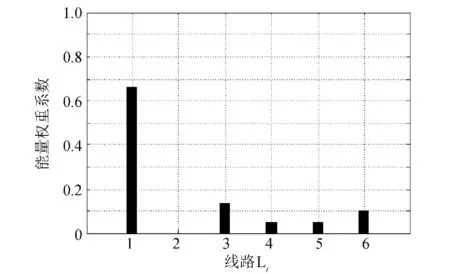
图9 线路1发生故障时各出线的能量权重系数Fig．9 The energy weighting coefficient of each line while single phase ground fault occurring in line 1

图10 母线发生故障时各出线的能量权重系数Fig．10 The energy weighting coefficient of each line while single phase ground fault occurring in bus bar

由于短路故障特征受故障点的位置、消弧线圈的补偿度、接地电阻、故障时相电压的大小等因素的影响，表2分情况讨论了该算法的选线结果，表中:p为消弧线圈的补偿度;φ为故障发生时相电压的相角;Rf为故障点电阻的大小;l为故障点到母线的距离;*代表空数据．设阈值Pset为0．5．

表2 故障选线结果Tab．2 Results of fault line－selection

6 结语

中性点经消弧线圈接地的配电网发生单相接地短路时，过渡过程中的容性电流的频率次数与感性电流的频率次数相差很大，因而二者不能相互补偿，而且所有线路的对地电容的充、放电电流都通过接地点流入故障点所在的线路中．据此，利用EEMD提出各个线路零序电流的高频分量和剩余分量，然后求取线路的能量权重系数，若所有线路能量权重系数都小于所设定的阈值，则母线发生了故障;否则能量权重系数大于阈值的线路为发生故障的线路．通过理论分析和大量仿真实验可得出如下结论:

1)与小波变换相比，EEMD具有根据信号的特征进行自适应分解的特点，克服了选取基函数的困难，而且EEMD比EMD能较好地分析瞬时性出现的信号．

2)该算法能准确、可靠地选出发生不同类型短路故障时的故障线路．

3)由于EEMD存在模态混叠和能量泄露等问题，虽然能够确保准确选出故障线路，但在求取线路的能量时存在误差，对EEMD算法的改进是今后研究的方向．