生产商提供价格折扣的供应链合作广告模型
陶 胜,刘慧琴
(闽南理工学院信息管理系,福建石狮362700)
Newsvendor型产品供应链协调问题是当今学界研究的热点问题,以往研究者在建模过程中均没有考虑广告费用,或者考虑了广告费用只是一方投入而另一方不愿投入的方式,这不满足市场竞争的需求,现实社会中广告费用都是由双方共同承担的,因此应对合作广告费用问题进行研究.谢金星等人(2006)[1]不仅考虑了制造商与销售商之间的Stackelberg合作广告博弈而且还考虑了制造商与销售商之间的垂直Nash博弈.Jin Feng Yue等人(2006)[2]将上述学者的工作推广到允许制造商提供价格折扣以刺激需求的情形,其假设了需求函数不仅与制造商和销售商各自的广告投入有关,而且还与制造商给予顾客的直接价格折扣有关.孙衍林(2007)[3]考虑在随机需求条件下,供应链上下游无合作时,需求方承担全部库存风险,其个体理性决策无法实现供应链的整体优化.Berk(2007)[4]根据缺货需求概率密度函数服从贝叶斯分布研究Newsvendor型产品,Lau A H和Lau H S(2007)[5]讨论的是价格折扣方面问题;Weng Z K(2004)[6]就制造商与销售商之间订货量的协调问题作了相关研究;王圣东(2008)[8]首次将直营店的模式引入到Newsvendor型产品合作广告问题中,给出了一种协调策略,使得制造商和销售商都愿意达成广告合作.
1 模型的建立与求解
本文考虑了由单一生产商与单一销售商组成的两层供应链,生产商生产某种Newsvendor型产品给销售商.在主从博弈假定下,生产商一方面要分摊销售商的一部分地方广告费用,另一方面要直接提供价格折扣给顾客,分析得出生产商最优地方广告费用的分摊比例以及最优价格折扣率的范围,并通过算法算出最优价格折扣率以及双方的最优利润.
关于Newsvendor型产品需求率,可从以下两方面来考虑:第一,需求率的不确定性;第二,广告宣传的影响,即与生产商的品牌广告投入和销售商的地方促销广告支出大小有关.此外,根据市场调查可知,若这两家的广告费用投入的越多,则消费者对该产品品牌的了解就越多,从而促使潜在消费者来购买该产品.但潜在消费者也是有限的,所以靠广告投入来影响需求不可能是无限增加的,最终会逼近于某个上界值.因此,假设Newsvendor型物品的期望需求是关于m和r增加的凹函数,其他研究者均采用了如下需求函数.
D(m,r)= α-βr-um-v.(1)
这里D(m,r)是关于r和m的不减函数,当地方促销广告费或品牌广告费用逼近零时或者两者同时逼近零时,则需求量D逼近常数α.
上述这种需求形式能全面地反映广告效应对需求的影响.但生产商为了提高利润,就会将品牌广告费用、地方促销费用、价格折扣三者联系起来加以考虑.本模型考虑生产商是直接提供价格折扣给消费者以刺激需求,设需求函数为
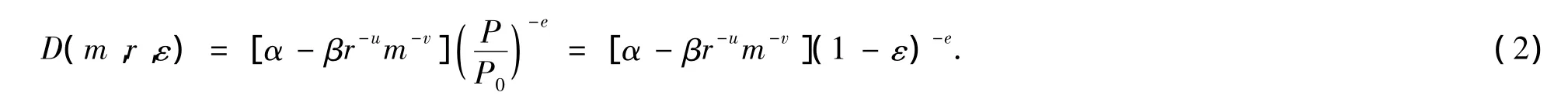
即需求的概率密度函数可表示为

则销售商的期望利润为
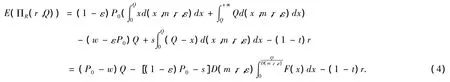
生产商的期望利润为

整个供应链的期望利润为

在独立决策下,生产商与销售商将遵从以生产商为主的Stackelberg博弈.因此生产商要先告知销售商,他所承担的品牌广告费用m以及地方促销广告费比例t;而销售商则要根据生产商的决策来确定使利润最大化的最优地方广告投入r以及最优订货量Q*.
当Q∈(0,+∞)时,有

即E(ΠR(r,Q))是关于变量Q是上凸函数,则存在唯一的最优订货量Q*,满足方程E(ΠR(r,Q))Q=0.
则有

于是

Q*=D(m,r,ε)Φ,其中

将(10)代入(4),可得

又因为
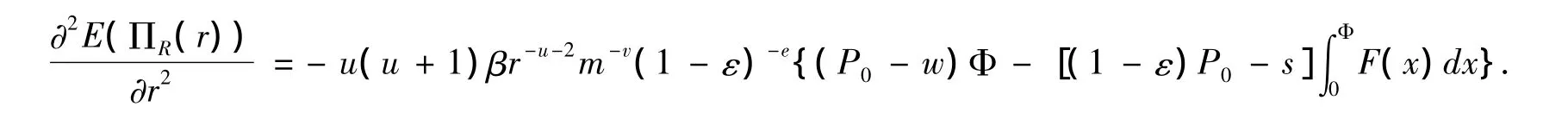
令

即E(ΠR(r))是关于地方促销广告费用r的凹函数.

而

接下来将给出生产商的最优策略.先将(2)和(10)代入(5),有

可得

又由

将(14)代入(15),则有

令


将(17)、(18)代入(10)、(12),则有

Q*=S(m*(ε),r*(ε),ε)Φ.则有

若 m*(ε),r*(ε)都是关于 ε 的增函数,则令h(ε)=(1-ε)-e[(w-εP0- c)Φ-Au],有即 e[(w -c)Φ -Au]-P0Φ -P0Φε(1 -e)> 0.
则若e<1时,有

若e>1时,有
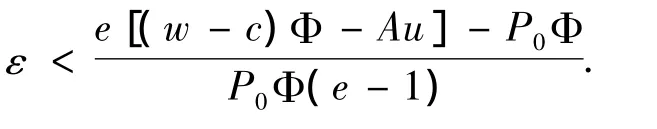
当0≤t*<1时,有
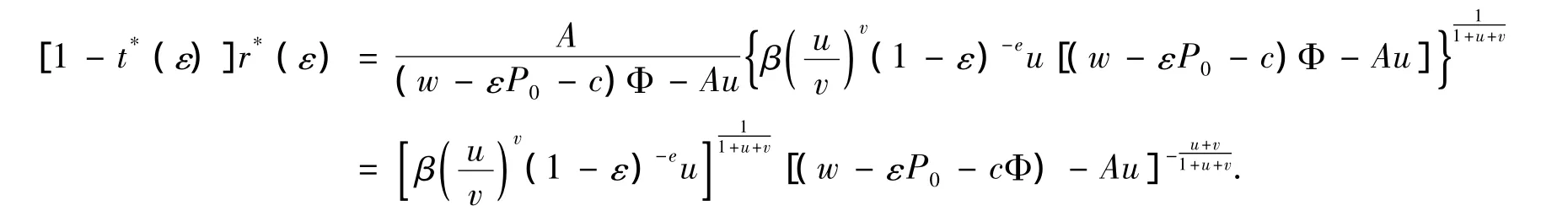
生产商分摊地方促销广告费用[1-t*(ε)]r*(ε)是关于ε的单调递增函数.因此,当生产商向消费者提供价格折扣时,销售商就会增加地方促销广告费用.
生产商愿意向消费者提供价格折扣主要基于以下因素:扩大市场占有份额;迫于同行业的竞争压力等.接下来,我们将研究生产商取得最大利润的价格折扣率ε*,为接近现实情况,下面只考虑在0≤t*<1的情形.
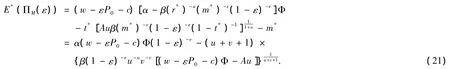
证明 因为

而函数E*(ΠM(ε))在ε=0的导数为
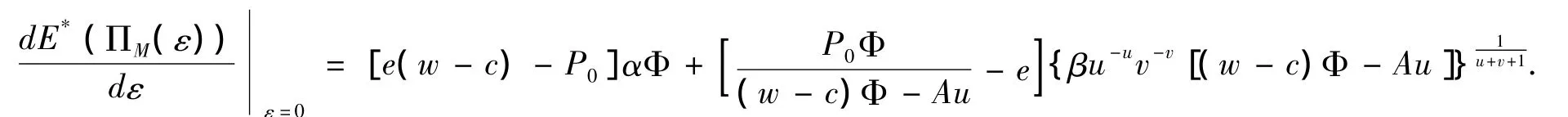
又因为0<ε<1,则有

因此,存在唯一的价格折扣率ε*使得制造商的利润达到最大.
在满足定理1的条件下,生产商需要决定当价格折扣率ε是多少时自己能获得最大利润,可由方程求出ε*.但由于计算比较复杂,这里我们仅能得到ε*的一个取值范围.
定理2 在定理1的条件下,ε*可被限制在ε1≤ε*≤ε2,其中
证明 因为

下面给出求解ε*的算法:
步骤1 在定理1的条件下,如果价格折扣能够使得制造商的利润增加,进入下一步,否则,ε*=0;
步骤2 定义θ为任意小的正常数,令ε=ε1;
步骤3 通过(21)计算E*(ΠM(ε));
步骤4 如果ε+θ>ε2,令ε*=ε停止.否则,通过(21)计算E*(ΠM(ε+θ));
步骤5 如果E*(ΠM(ε+θ))≤E*(ΠM(ε)),令ε*=ε停止.否则,令ε =ε+θ,进入步骤4.
上述算法将会得到一个价格折扣率,它通过θ的值得到最优的价格折扣率ε*.然后将ε*代替ε代入(17)、(18)、(19),得到生产商的最优品牌广告投入、地方促销广告费用、生产商的地方促销费用的投入比例.类似地,将ε*代替ε代入(4)和(21),我们能分别得到生产商和销售商的最优利润,以及整个供应链的利润.
2 应用举例
为说明本模型的现实性,现设模型中的参数值如下:c=40,w=60,P0=105,s=10,α =5000,β =4*107,u=0.4,v=0.55,e=2,且 X 是期望为 1.
利用本模型提供的算法可得,在制造商与销售商的独立决策下的最优策略及有关的期望利润值是:ε*=0.15760,t*=0.17912,r*=18837.65,m*=25901.78,Q*=1578.71,E*(ΠM)=2371.52,E*(ΠR)=3789.73,E*(Πs)=6161.25.
3 结语
本文提出生产商分担销售商的地方促销广告费用,且生产商直接让利于消费者,并证明了生产商的利润存在唯一最大值,由数值计算能够得出最优价格折扣率和该模型问题中的其他最优值,对解决实际问题有一定的参考价值.
[1]Xie J,Ai S.A note on“Cooperative advertising,game theory and manufacturer- retailer supply chains”[J].Omega,2006,34(5):501-504.
[2]Yue J,Austin J,Wang M C,et al.Coordination of cooperative advertising in a two-level supply chain when manufacturer offers discount[J].European Journal of Operational Research,2006,168(1):65 -85.
[3]孙衍林,徐学军.单周期随机需求下供应链库存协调机制设计[J].工业工程,2007,10(3):15-19.
[4]Berk,et al.Bayesian demand updating in the lost sales newsvendor problem:A two moment approximation[J].European of Operational Research,2007,182(1):256 -277.
[5]Lau A H,Lau H S,Wang J C.Designing a quantity discount scheme for a newsvendor type product with numerous heterogeneous retailers[J].European of Operational Research,2007,180(2):585 -600.
[6]Weng Z K.Coordinating order quantities between the manufacturer and the buyer:A generalized newsvendor model[J].European of Operational Research,2004,156(1):148 -161.
[7]王圣东,周永务.带有两种营销模式的供应链合作广告协调模型[J].系统工程学报,2008,23(6):674-682.

