具有左中心幂等元的完美l-ample半群

·数理科学·

具有左中心幂等元的完美l-ample半群

孙燕,王旭东,任学明

(西安建筑科技大学 理学院, 陕西 西安710055)

摘要：定义完美l-ample半群,并研究具有左中心幂等元的完美l-ample半群的半格分解。利用半格分解,证明了半群S为具有左中心幂等元的完美l-ample半群,当且仅当S为直积Mα×Λα的强半格,其中Mα是右可消幂幺半群,Λα是右零带。这一结果为具有左中心幂等元的完美l-ample半群结构的建立奠定了基础。

关键词：完美l-ample半群;左中心幂等元;强半格;[*,～]-格林关系

收稿日期：2014-01-13

基金项目：国家自然科学基金资助项目(11471255，11326204)； 陕西省教育厅专项科研计划基金资助项目 (14JK1412)；校青年基金资助项目(QN1134)

作者简介：孙燕, 女, 山东平度人, 从事半群代数理论研究。

中图分类号：O152.7

Perfect l-ample semigroups with left central idempotents

SUN Yan, WANY Xu-dong, REN Xue-ming

(School of Science, Xi′an University of Architecture and Technology, Xi′an 710055， China)

Abstract:The concept of perfect l-ample semigroups is introduced and the semilattice decomposition of perfect l-ample semigroups with left central idempotents is studied. By using this semilattice decomposition, it is proved that a semigroup S is a perfect l-ample semigroup with left central idempotents if and only if it is a strong semilattice of a direct product Mα×Λα, where Mα is a right cancellative unipotent monoid and Λα is a right zero band.This result is the basis that the structure theorem of perfect l-ample semigroups with left central idempotents can be established.

Key words: perfect l-ample semigroup;left central idempotent;strong semilattice;[*,～]-Green′s relation

含有单位元的半群称为幺半群。只含有一个幂等元的幺半群称为幂幺半群。半群S称为富足半群,如果S的每一个L*-类和每一个R*-类均含有幂等元[2]。半群S称为l-ample半群,如果S的每一个L[*,～]-类和每一个R[*,～]-类均含有幂等元。我们易证L⊆L*⊆L[*,～],R⊆R*=R[*,～]。从这一结果不难看出,富足半群一定是l-ample半群,但l-ample半群不一定是富足半群。从而l-ample半群是富足半群在广义正则半群类中的一个推广。

在正则半群的研究方面,众所周知,Clifford半群是群的强半格[3]。而在富足半群的研究方面,Fountain深入研究了具有中心幂等元的适当半群[4]。K.P.Shum和任学明又给出了具有左中心幂等元的富足半群的相关定理[5]。

在这一背景下,自然地,人们会寻求l-ample半群关于富足半群的类似物。为此,本文受Shum的启发引入了完美l-ample半群的概念,借助[*,～]-格林关系,证明了半群S是一个具有左中心幂等元的完美l-ample半群,当且仅当S是直积Mα×Λα的强半格,其中Mα为右可消幂幺半群,Λα为右零带。将文献[3],[4]和[5]的结论推广到具有左中心幂等元的完美l-ample半群中。从而Clifford,Fountain和Shum的结论都可类似地应用于此。

文中未给出的术语和记号见文献[1],[2]和[6]。

1若干准备

本文首先给出具有左中心幂等元的完美l-ample半群的基本概念和若干性质。

定义1[6]半群S的幂等元e称为左中心的,如果关于任意x,y∈S1,且y≠1,有xey=exy。

定义2l-ample半群S称为完美l-ample半群,如果L[*,～]满足右同余条件,即L[*,～]是S上的右同余。

命题1 令S为一半群,且a,b∈S。则下列两款成立:

(i) (a,b)∈L[*,～],当且仅当关于任意e∈E, ae=a⟺be=b;

(ii) (a,b)∈R[*,～],当且仅当关于任意x,y∈S1, xa=ya⟺xb=yb。

命题2[2]令S为一半群,且a,b∈S。则下列两款成立:

(i) (a,b)∈R[*,～],当且仅当关于任意x,y∈S1,xa=ya⟺xb=yb;

(ii) 关于任意幂等元e∈S,(e,a)∈R[*,～],当且仅当ea=a,且关于任意x,y∈S1,xa=ya⟹xe=ye。

特别地,若a,b为半群S的正则元,则(a,b)∈L[*,～],当且仅当(a,b)∈L,这里L表示通常的格林关系[7]。对偶地,关于R[*,～]的相应结论亦成立。

引理1S的每个L[*,～]-类都含有唯一幂等元。

证 明假设e,f∈E,且(e,f)∈L[*,～],则(e,f)∈L。故结论易证。

引理2 格林关系L[*,～]为S上的同余。

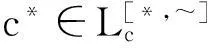
引理3关于任意a,b∈S,恒有(ab)*=a*b*。

证 明事实上,关于任意b∈S,存在唯一幂等元b*∈S∩E使得(b,b*)∈L[*,～]。因为L[*,～]是具有左中心幂等元的完美l-ample半群S上的同余,所以关于任意a∈S,有(ab,ab*)∈L[*,～]。从而据引理1,知(ab)*=(ab*)*。类似可证,(ab*,a*b*)∈L[*,～]。又据引理1,知(ab*)*=(a*b*)*=a*b*。因此,(ab)*=(ab*)*=a*b*。这样就完成了引理3的证明。

引理4在具有左中心幂等元的完美l-ample半群S上定义关系σ如下:

aσb,当且仅当a*b*=b*和b*a*=a*。

证 明易验证σ为S上的等价关系。设a,b∈S,且a,b∈σ,则有a*b*=b*和b*a*=a*。据引理3和幂等元b*是左中心的,知关于任意c∈S,有(ac)*(bc)*=a*c*b*c*=a*b*c*=b*c*=(bc)*。类似地,可证(bc)*(ac)*=(ac)*。这验证了(ac,bc)∈σ。同理,可得(ca,cb)∈σ。因此,σ为S上的同余。现在,据引理3和幂等元a*是左中心的,知 (ab)*(ba)*=a*b*a*=b*a*a*=(ba)*和(ba)*(ab)*=(ab)*。从而据上述σ的定义,不难知(ab,ba)∈σ。此外,关于任意a∈S,我们显然有(a,a*)∈σ和(a,a2)∈σ。这样,σ确实是具有左中心幂等元的完美l-ample半群S上的半格同余。故结论得证。

引理5令S为具有左中心幂等元的完美l-ample半群。则下列两款成立:

(i) L[*,～]=H[*,～]且σ=R[*,～]=D[*,～];

(ii) H[*,～],R[*,～]和D[*,～]都是S上的同余。

证 明(i) 因为S是l-ample半群。所以,关于任意a∈S,存在e∈E使得(a,e)∈R[*,～]。这说明了ea=a。于是,据引理3,知ea*=a*。另外,因为(a,a*)∈L[*,～]和a*是左中心幂等元,所以a=aa*=aa*a*=a*aa*=a*a,即a*a=a。从而据(a,e)∈R[*,～]和命题2(ii),知a*e=e。由此,再结合前述ea*=a*,知(a*,e)∈R,这导致了(a*,e)∈R[*,～]。因此,(a,a*)∈R[*,～]。又据(a,a*)∈L[*,～],立即有(a,a*)∈H[*,～]。现在,令a,b∈S,且(a,b)∈L[*,～]。则(a,a*)∈H[*,～],(b,b*)∈H[*,～]。据引理1知a*=b*。因此,(a,b)∈H[*,～]。这导致了L[*,～]⊆H[*,～]。从而不难知道,L[*,～]=H[*,～]。至此,这证明了L[*,～]=H[*,～]⊆R[*,～]。

设a,b∈S,且(a,b)∈R[*,～]。则据L[*,～]⊆R[*,～],知(a*,b*)∈R[*,～]。从而有a*b*=b*和b*a*=a*。因此,据关系σ的定义,可知(a,b)∈σ。这证明了R[*,～]⊆σ。另一方面,设a,b∈S,且(a,b)∈σ,则有a*b*=b*和b*a*=a*。由R关系[6]的定义,知(a*,b*)∈R。这导致了(a*,b*)∈R[*,～]。而且据(a,a*)∈L[*,～]和L[*,～]⊆R[*,～],知(a,a*)∈R[*,～]。类似地,(b,b*)∈R[*,～]。从而(a,b)∈R[*,～]。这证明了σ⊆R[*,～]。因此,可得σ=R[*,～]。容易验证D[*,～]=L[*,～]∨R[*,～]=H[*,～]∨R[*,～]=R[*,～]。这样,可以断定σ=R[*,～]=D[*,～]。

(ii) 据引理2和引理4,易知H[*,～],R[*,～]和D[*,～]都是S上的同余。这样就完成了引理5的证明。

2主要结论

现在,我们将给出具有左中心幂等元的完美l-ample半群的重要定理。

定理1令S为一半群。则下列各款等价:

(i) S为具有左中心幂等元的完美l-ample半群;

(ii) S为直积Mα×Λα的半格,其中Mα是右可消幂幺半群,Λα是右零带。而且半群S的幂等元集E形成右正规带;

(iii) S为直积Mα×Λα的强半格,其中Mα是右可消幂幺半群,Λα是右零带。

证 明(i)⟹(ii)显然,S=∪α∈YSα, 其中Sα为半群S关于半格Y的一个σ-类。因为S是U-富足半群且σ=R[*,～],所以Sα∩E≠∅。由此,关于某个固定eα∈Sα∩E,令Mα=Sαeα。显然，Mα为含有恒等元eα的幺半群, 记eα=1α。 接着，证明Mα为右可消的。关于a,b,c∈Mα,令ab=cb。则由(eα,b)∈R[*,～]和命题1(ii),有aeα=ceα。据eα为Mα的恒等元,知a=c。因此,Mα为右可消的幺半群。事实上,Mα=L[*,～]=H[*,～]。于是,Mα中只含有一个幂等元。因此,Mα为右可消幂幺半群。现在,令Λα为Sα的幂等元集,即Λα=Sα∩E。则关于任意e,f∈Λα,显然有(e,f)∈R[*,～]。这意味着Λα是右零带。关于任意(x,f)∈Mα×Λα,我们定义映射φ:Mα×Λα→Sα,且满足φ(x,f)=xf，则关于任意(x,f),(y,g)∈Mα×Λα,有

φ(x,f)φ(y,g)=xfyg=

xyfg=xyg=φ[(x,f)(y,g)]。

于是,φ为一同态。

另外,若φ(x,f)=φ(y,g),则xf=yg，从而xfeα=ygeα。又因为Λα是右零带且eα为Mα的恒等元,所以x=y。与此同时,可得xf=xg。从而由引理3,有x*f=x*g。再据Λα是右零带,知f=g。这证明了φ也是一个单同态。

下面证明映射φ是满射。关于任意a∈Sα,存在唯一幂等元a*使得(a,a*)∈L[*,～]。据引理5,知L[*,～]⊆R[*,～]且σ=R[*,～]。从而(a,a*)∈σ。这导致了a*∈Sα。因此,a*∈Λα=Sα∩E。另外,由Sα∩E≠∅,知关于某个固定eα∈Sα∩E,有aeα∈Mα。在这种情形下,因为Λα为右零带且(a,a*)∈L[*,～]。所以，总有

(aeα,a*)φ=aeαa*=aa*=a。

这证明了映射φ是满射。

综上,Sα≅Mα×Λα。

最后,因为任意e∈E是左中心幂等元,所以关于任意e,f,g∈E,都有efg=feg。这证明了E是右正规带。

(ii)⟹(iii)为证S是直积Mα×Λα的强半格,我们选择任意α,β∈Y,且α≥β。首先,令a∈Sα,eβ∈Sβ∩E。则eβa∈Sβ。基于这一事实,关于任意a∈Sα和某个固定eβ∈Sβ∩E，建立映射θα,β:Sα→Sβ,且满足aθα,β=eβa,其中α≥β。令eβa=(u,i)∈Sβ,eβ=(1β,j)∈Sβ∩E,g=(1β,i)∈Sβ∩E,其中1β是Mβ中的恒等元。则

eβag=(u,i)(1β,i)=(u,i)=eβa,

(1)

g=(1β,i)=(1β,j)(1β,i)=eβg。

(2)

类似地,令b=(v,l)∈Sα,h=(1α,l)∈Sα∩E。则

hb=b。

(3)

而且由E为右正则带,有

geβh=eβgh。

(4)

据式(1),(2),(3)和(4),知

eβaeβb=eβageβhb=

eβaeβghb=eβaghb=eβab，

从而aθα,βbθα,β=(ab)θα,β。这证明了θα,β为一同态。

另一方面,关于任意α∈Y,不难看出θα,α=1Sα。

现在,令a=(w,k)∈Sα,p=(1α,k)∈Sα∩E,其中α∈Y。则有pa=a。若α≥β≥γ,则关于某个固定eβ∈Sβ∩E和某个固定eγ∈Sγ∩E,据E为右正则带,知eγeβp=eβeγp=eβeγ·eγp=eγp。从而

aθα,βθβ,γ=eγ(eβa)=

eγeβpa=eγpa=eγa=aθα,γ。

因此,θα,γ=θα,βθβ,γ。

最后,关于任意α,β∈Y,令a∈Sα,b∈Sβ，则关于某个固定eαβ∈Sαβ∩E,有ab=eαβ(ab)。因为eαβa∈Sαβ,利用式(1),知存在f2=f∈Sαβ使得eαβaf=eαβa。而且关于b∈Sβ,利用式(3),知存在e2=e∈Sβ使得eb=b。再根据E的右正规性,有

eαβaeαβb=eαβafeαβeb=eαβaeαβfeb=

eαβa(eαβf)eb=eαβafeb=eαβab=ab。

这证明了ab=aθα,αβ·bθβ,αβ。因此,S为直积Mα×Λα的强半格。记为S=[Y;Sα,θα,β],其中Sα=Mα×Λα。

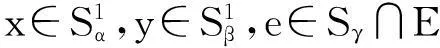
xey=(m,t)θα,δ·(1γ,q)θγ,δ·(v,l)θβ,δ=

(mθα,δ·vθβ,δ,lθβ,δ)。

类似地,exy=(mθα,δ·vθβ,δ,lθβ,δ)。从而xey=exy。这样,证明了关于任意e∈E,都有幂等元e是左中心的。换句话说,半群S是具有左中心幂等元的半群。

进一步,证明半群S的每个L[*,～]-类中含有幂等元。关于任意α∈Y,令a=(u,i)∈Sα,f=(1α,i)=Sα∩E。为证明(a,f)∈L[*,～],关于任意e∈E,假设ae=a,则存在某个γ∈Y使得e∈Sγ∩E。而且因为S是Sα的半格,所以关于α,γ∈Y,有γ≥α。并且令e=(1γ,k)∈Sγ∩E。据ae=a,有

(u,i)(1γ,k)=(u,i)θα,α·(1γ,k)θγ,α=

(u,kθγ,α)=(u,i)。

这意味着kθγ,α=i。因此,

fe=(1α,i)(1γ,k)=

(1α,i)θα,α·(1γ,k)θγ,α=

(1α,kθγ,α)=(1α,i)=f。

同理,关于任意e∈E,若fe=f,则ae=a。从而据命题1(i),知(a,f)∈L[*,～]。这样,半群的每个L[*,～]-类中含有幂等元。

另一方面,证明半群S的每个R[*,～]-类中含有幂等元。令b=(w,h)∈Sα,g=(1α,h)∈Sα∩E。则gb=b。为了证明(b,g)∈R[*,～]。关于任意x,y∈S1,假设xb=yb,则存在某个β,γ∈Y使得x∈Sβ,y∈Sγ,而且知αβ=αγ。又令x=(m,t)∈Sβ,y=(v,l)∈Sγ，则由半群S是半群Sα的强半格,知

xb=(m,t)θβ,αβ·(w,h)θα,αβ=(mθβ,αβ·wθα,αβ,hθα,αβ),

yb=(v,l)θγ,αγ·(w,h)θα,αγ=(vθγ,αγ·wθα,αγ,hθα,αγ)=(vθγ,αβ·wθα,αβ,hθα,αβ)。

据xb=yb,知mθβ,αβ·wθα,αβ=vθγ,αβ·wθα,αβ。又因为Mαβ是右可消幺半群。所以,mθβ,αβ=vθγ,αβ。从而

xg=(m,t)θβ,αβ·(1α,h)θα,αβ=(mθβ,αβ,hθα,αβ)=(vθγ,αβ,hθα,αβ)=(vθγ,αγ,hθα,αγ)=yg。

再据命题2(ii),知(b,g)∈R[*,～]。因此,半群S的每个R[*,～]也含有幂等元。至此,证明了半群S确实是l-ample半群。

最后,我们来证明L[*,～]是半群S上的右同余。关于a,b∈S,若(a,b)∈L[*,～], 则元素a,b在同一个Sα里,其中α∈Y。因为如果a,b∈L[*,～],但a∈Sα,b∈Sβ的话,则据S为l-ample半群,知存在f2=f∈Sα∩E和g2=g∈Sβ∩E，使得(a,f)∈L[*,～]和(b,g)∈L[*,～]。这意味着(f,g)∈L[*,～]，从而fg=f,gf=g,其中fg,gf∈Sαβ,f∈Sα和g∈Sβ。因此,α=β。基于此事实，假设(a,b)∈L[*,～],则存在某个α∈Y使得a,b∈Sα。又令a=(u,i)∈Sα,b=(w,h)∈Sα。则为了证明关于任意c∈S,都有(ac,bc)∈L[*,～]成立。于是,关于任意e∈E，假设ace=ac,则存在某个β,γ∈Y使得c∈Sβ,e∈Sγ∩E。而且由S是半群Sα的强半格,知α,β≤γ。令c=(n,j)∈Sβ,e=(1γ,k)∈Sγ∩E，则由假设ace=ac,知

(u,i)(n,j)(1γ,k)=

(u,i)θα,αβ·(n,j)θβ,αβ·(1γ,k)θγ,αβ=

(uθα,αβ·nθβ,αβ,kθγ,αβ)=

(uθα,αβ·nθβ,αβ,jθβ,αβ)。

这导致了kθγ,αβ=jθβ,αβ。因此,

bce=(w,h)θα,αβ·(n,j)θβ,αβ·(1γ,k)θγ,αβ=

(wθα,αβ·nθβ,αβ,kθγ,αβ)=

(wθα,αβ·nθβ,αβ,jθβ,αβ)=bc。

类似可得,关于任意e∈E,若bce=bc,则ace=ac。从而据命题1(i),知(ac,bc)∈L[*,～]。这样,L[*,～]是S上的右同余。因此,半群S为完美l-ample半群。

综上所述,半群S为具有左中心幂等元的完美l-ample半群。这样就完成了定理1的证明。

注1上述定理推广了K.P.Shum和任学明的相关结论(见文献[5], 定理3.1)。

下面主要结果的证明类似于定理1的证明方法。

推论1令S为一半群。则下列各款等价:

(i) S为具有左中心幂等元的正则半群;

(ii) S为右群的强半格;

(iii) S为右Clifford半群,且E形成右正规带。

证 明首先注意到在正则半群上L[*,～]=L,R[*,～]=R。因此,类似于定理1的证明,有(i)⟹(ii)。详细证明略。关于(ii)⟹(iii)和(iii)⟹(i)直接由文献[8]中定理4.1可知。故结论可得。

注上述定理推广了著名的Clifford 定理(见文献[6],定理2.1)。

参考文献：

[1]LAWSON M V.Rees matrix semigroups [J].Proc Edinburgh Math Soc,1990,33:23-37.

[2]FOUNTAIN J B.Abundant semigroups [J].Proc London Math Soc,1982,44 (3):103-129.

[3]CLIFFORD A H.Semigroups admitting relatives inverse [J].Ann of Math,1941,42:1037-1049.

[4]FOUNTAIN J B.Adequate semigroups [J].Proc Edinburgh Math Soc,1979,22:113-125.

[5]SHUM K P,REN Xue-ming.Abundant semigroups with left central idempotents [J].Pure Mathematics and Applications,1999,10 (1):109-113.

[6]HOWIE J M.An introduction to semigroup theory [M].London:Academic Press,1976.

[7]GUO Yu-qi,SHUM K P,GONG Chun-mei.On (*,～)-Green′s relations and ortho-lc-monoids [J].Communications in Algebra,2011,39:5-31.

[8]ZHU Pin-yu,GUO Yu-qi,SHUM K P.Structure and characterizations of left C-semigroups [J].Science in China(Series A),1992,6:791-805.

(编辑亢小玉)