机动飞行器多终端约束反演滑模末端导引方法
洪功名,陈万春
(北京航空航天大学 宇航学院,北京100191)
0 引言
机动飞行器在攻击目标时,不但需要考虑减小脱靶量,而且某些特殊的战斗部期望以一定的角度命中目标,从而获得更好的毁伤效果。如某些再入机动弹头在其末制导段,需要飞行的速度方向基本与地面垂直,这样可以使得末制导系统正常工作。另外,弹头为获得最大的侵彻深度,需要最终以一定碰撞角命中目标。因此,终端角度的控制已成为精确打击武器的一项重要性能。
文献[1]在1973年首先给出一种带落角约束形式的末制导律。经过多年的发展,国内外对有关带角度约束的制导律设计已经有许多比较成熟的研究,部分成果已经在实际中开始应用。在设计带角度约束的制导律时,常用的设计思想是基于比例导引律并附加偏置项[2]、基于最优控制理论[3],或基于变结构控制。
变结构控制中的反演设计(Backstepping)[4]是将Lyapunov函数的选取与控制器的设计相结合的一种回归设计方法。它通过从系统最低阶次微分方程开始,逐层镇定设计最终达到全局镇定,从而给出整个系统的控制律。滑模变结构控制对参数不确定性和外界干扰具有较强的鲁棒性,国内外近些年来将反演滑模设计方法运用到带角度约束的制导律设计上也取得了一些进展。贾庆忠等[5]运用反演递推设计方法,得到适用于仅有角度测量的航空侵彻炸弹的带末端落角约束的制导律。文献[6]运用反演设计方法,通过设计合适的Lyapunov函数,给出能满足终端角度约束的巡航导弹和可重复使用飞行器RLV着陆段的末制导律,不同初始条件以及气动条件下的仿真结果显示,该制导律具有很好的制导精度以及一定的鲁棒性。但是这些都没有考虑终端法向过载约束,仿真结果显示末端可能出现较大的法向加速度,在环境及相关参数不确定性情况下容易出现明显的脱靶量。
许多文献在求解带角度约束末制导律时,依赖对运动方程的线性化,得出解析形式的制导律。当需要考虑的终端约束较多时,制导律的结果较为复杂。众所周知,高阶滑模的滑动变量及其一定阶导数具有在有限时间内收敛的特点,本文利用反演滑模设计方法,不依赖运动方程的线性化,通过设计合适的滑动面,使滑动变量及其各阶导数渐进收敛于零来逐阶满足各个终端约束,最终给出整个系统的制导方法。在推导末制导律时考虑了终端法向过载约束,仿真结果显示飞行器在接近目标时法向加速度很小,这样可以近似保证弹头在弹体轴方向与速度方向近似重合的情况下命中目标,从而提高弹头的作战效能。
1 数学模型
1.1 机动飞行器末制导段数学模型
为了简化问题,以固定目标和飞行器质心为基准,将飞行器运动分解为俯仰平面和转弯平面[3]。研究飞行器在质心M、目标T和地心所确定的俯仰平面内运动。将飞行器和目标都看作质点,弹-目关系示意图如图1所示。

图1 弹-目关系示意图Fig.1 Geometry of vehicle-target positions
图中:T为目标的位置;xB为弹体轴;H为高度;x为纵向射程;LOS为视线;λ为视线角;V为飞行器的速度;γ为弹道倾角,以速度方向绕水平方向逆时针转动为正;α为迎角,以弹体轴方向绕速度方向逆时针转动为正;θ为俯仰角,以弹体轴方向绕水平方向逆时针转动为正;am为法向加速度。运动学方程为:

式中:D为阻力;m为质量;g为重力加速度;L为升力。
1.2 终端约束
为提高弹头的作战效能,一般要求机动飞行器能以一定落角或弹道倾角命中目标,即终端弹道倾角要求满足约束γend=γF,γF为需求的终端弹道倾角。除此之外,终端法向过载较大,容易在环境及相关参数不确定性下出现较明显的脱靶量。另一个需要考虑的终端约束是法向加速度,即am,end=0。弹头一般为轴对称,终端法向加速度为零,可以使得迎角较小,由于θ≈α+γ,这样弹头(即弹体轴)能够近似与速度方向一致。
1.3 反演设计
对于一个高阶系统,其n-1阶导数已知,并有:

设计高阶滑模变结构控制u,使得f(x)及其n-1阶导数:

在有限时间内实现。可以运用如下反演设计方法[4],在此考虑最常用的二阶系统,有:

令滑动面为:

可设候补Lyapunov函数为:

求导得:

为保证滑动面s1在有限的时间内趋近于零,必须选择合适的使得负定。文献[6]给出一种的选择方法:
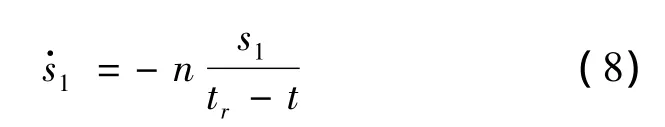
式中:n为大于1的正常系数;tr为趋近零的时刻。这样选择可以保证滑动面s1在tr时刻趋近零,在运用制导律时可将tr-t用剩余飞行时间Tgo代替。
由于系统相对阶为2,再设滑动面

考虑候补Lyapunov函数

求导得:

在此,可令趋近律为:

式中:η,K为正数,其大小影响收敛速度。对s2求导得:

式中出现了控制项,联立式(12)和式(13),可得控制u表达式为:

为削弱符号函数引起的颤振,最常用的方法是用饱和函数sat(s)[4]代替理想滑动模态中的符号函数sign(s)。
2 设计末制导律
末制导律的设计分为俯仰平面和转弯平面,转弯平面的最优制导律为比例导引律[3],不需要再设计,所以本文只设计俯仰平面内的制导律。
需要考虑的终端约束有弹道倾角和法向加速度约束,而飞行器最终需要命中目标,加上射程约束,共有3个约束。因此,末制导律的设计是一个三阶滑模控制问题,关键是滑动面f(x)的选取。
第一个约束是射程,f→0可以保证飞行器命中目标。而位移的一阶导数为速度,考虑到飞行器的纵向速度与弹道倾角直接相关,因此设计第二个约束为纵向速度,f'→0可以保证终端弹道倾角满足约束要求;位移的二阶导数为加速度,射程的二阶导数即弹道倾角的一阶导数为法向加速度,f″→0可以保证终端法向加速度满足约束要求。另外,垂直方向上命中目标是由剩余飞行时间趋向于零来保证的。有了以上的分析,构造滑动面如下:

式中:T为目标位置;x为当前飞行器纵向位置;V为速度;γF为终端约束要求的最终弹道倾角。s→0可以使得最终脱靶量为零,满足射程要求,从而命中目标。假设速度项不变(实际中变化较小),对式(15)求导可得:


式中:am为法向加速度。由于大落角再入时sinγ不为零,因此s¨→0可以保证最终的法向加速度为零,从而间接使得最终的迎角很小。在此可以将飞行控制系统用一阶延迟环节表示,指令加速度与实际加速度之间有如下关系:

式中:Tα为飞行控制系统时间常数;acmd为指令加速度。继续对式(18)求导可得:

式中出现了控制项指令加速度u(acmd),因此根据反演设计方法,可求得控制u(acmd)为:

其中:

根据上述制导律得出指令加速度u(acmd)后,即可求得相应的指令迎角αcmd。
3 制导方案
典型再入机动飞行器,如美国的潘兴-2导弹[7]的机动弹头,当弹头到达目标区上空45 km左右高度,开始将弹道拉起。考虑到热防护,弹头在这一阶段近似保持最大迎角飞行。弹道拉起后有一段近似平飞段,在惯性制导系统控制下进行减速控制。最后进行下拉导引控制,控制弹道倾角满足相关约束,同时命中目标。根据再入机动弹头弹道的特点,设计如下制导方案:
(1)弹道拉起段
此段由空气舵产生弹头最大的可用迎角。转弯平面内利用的比例导引律产生侧滑角指令控制弹头方向近似指向目标,这样可以使得弹头在飞行到下拉导引段时,近似为俯仰平面的控制。
(2)平飞减速段
此段弹头可以进行减速控制,如锥形减速。即弹头用于控制弹道倾角的配平迎角为零,并以一定的总迎角绕弹头速度方向以一定的角速率旋转。
(3)下拉导引段
此段弹头俯仰平面内控制由本文给出的末制导律来控制,转弯平面内由比例导引律控制。这样可以使得弹头准确命中目标,同时满足各终端角度约束。
4 仿真结果及分析
再入机动弹头再入初始点运动参数为:速度V0=2 000 m/s,弹道倾角 γ0= - 45 °,高度 H0=45 km。终端约束为:目标位置x=70 km,终端法向过载约束 am,end=0。另外,最大迎角约束 αmax=25°,最大侧滑角βmax=15°。分别考虑终端弹道倾角约束 γF= -90°,-80°,-70°,-60°的情况,仿真结果如图2~图4所示。

图2 弹道曲线Fig.2 Trajectory profile
图2 为射程高度曲线,可以看出不同终端弹道倾角约束下,本文制导方法都能导引弹头准确命中目标,机动弹道明显的特点为先拉起,近似平飞,最后下拉以一定角度命中目标。

图3 弹道倾角曲线Fig.3 Flight path angle profile

图4 法向过载曲线Fig.4 Normal overload profile
图3 为相应的弹道倾角曲线,仿真结果显示弹道倾角最终都能满足约束要求。图4为相应的法向过载曲线,显示本文方法最终法向过载非常小,理想情况下的仿真结果终端法向过载小于0.02。
图5给出了终端倾角约束为-90°情况下,末制导段的滑动变量及其一、二阶导数随时间变化情况。可以看出,滑动变量及其一、二阶导数都能渐进收敛到零,满足相应的终端约束。

图5 末制导段滑动变量s,s',s″曲线Fig.5 Sliding surface profile in terminal guidance
为了更加清楚地显示本文制导律在末制导段的特点,对比分析下拉导引段的仿真结果。将本文提出的制导方案(BDTG)与经典的弹道整形制导律(TSGL)在相同条件下进行仿真对比。经典的TSGL[8]为:

式中:nc为指令加速度;Vc为相对速度为视线角速率。设计下拉导引段仿真初始高度H0=10 km,初始弹道倾角γ0=-10°,迎角为0°,分两种情形进行仿真,分别距离目标纵向剩余射程Rgo=6 km和Rgo=10 km,图6和图7给出了仿真结果对比。

图6 纵向射程6 km时弹道曲线、法向过载曲线Fig.6 Contrast trajectory and normal overload profile for 6 km downrange case

图7 纵向射程10 km时弹道曲线、法向过载曲线Fig.7 Contrast trajectory and normal overload profile for 10 km downrange case
图7 的法向过载曲线中,BDTG法仿真结果最开始法向过载为零,是由于末制导律在靠近目标一定距离才开始导引而导致的。从法向过载曲线对比图可以看出,为了使得最终的法向过载近似为零,本文的制导方法能够使飞行器在距离目标一定距离时维持一段较长时间大过载的下拉导引,使得弹道迅速下压,之后法向过载平缓降低到接近零。从弹道曲线可以看出,本文制导方法使得弹道更加快速下压,转向垂直状态。TSGL法的仿真结果显示,飞行器在靠近目标时,剩余飞行时间较小造成指令加速度较大,最终法向过载容易出现跳动,如果存在气动、环境等不确定性,则容易造成明显的脱靶。
在仿真时考虑存在多种扰动情况,进一步验证本文制导方法的鲁棒性。扰动主要有参数不确定性、外界的干扰和测量误差。参数不确定性主要考虑气动力系数拉偏和大气参数不确定性:由于与法向加速度直接相关的是升力系数,在此将升力系数拉偏±20%,大气密度拉偏±20%。外界的干扰主要考虑纵向风的影响,风向考虑与飞行器飞行方向同向、反向两种方向,风场数据参考CIRA-86,图8给出了风速随高度变化曲线,横坐标Vwind表示风速。

图8 风场模型Fig.8 Wind field model
仿真时运用制导律给出指令,需要当前弹道倾角、剩余飞行时间等信息,实际中有测量误差,可加入高斯白噪声来模拟。上述三种扰动(气动力系数、大气密度正负拉偏和风向)组合,共8种情形,加上理想情形,总共9次仿真结果的终端误差数据如表1所示(射程脱靶量均较小,小于0.1 m,故表中没有列举)。
表中,第1列为仿真的扰动:“同”指风向与飞行器飞行方向一致,“反”则相反;中间的数字代表大气密度拉偏量,第3个数字代表气动力系数拉偏量。

表1 多扰动下的终端误差对比Table 1 Terminal errors of flight path angle and normal overload under multiple disturbances
从仿真结果可以看出,运用本文的制导方法,终端弹道倾角误差非常小,在10-4量级,最终法向过载小于0.3。由于扰动的存在,运用弹道整形制导律仿真结果的最终法向过载存在较大不确定性,而且弹道倾角误差相比也大许多。
仿真结果还显示,弹头末速度约为900~1 100 m/s,机动弹头要求撞击地面的速度为410~1 070 m/s[7],可以进行适当的附加减速控制。本文设计的制导方案中,预留了一段平飞减速段,从图3中可以看出有一段10~15 s的近似平飞段,可以用于减速控制,初步仿真表明,平飞段锥形减速可以有最大300 m/s的最终附加减速效果。
5 结束语
针对机动飞行器带终端约束的末制导问题,本文基于反演设计方法,通过设计合适的滑动面,将高阶滑模的滑动变量及其一定阶导数在有限时间内渐进收敛的特点与各个终端约束相结合,得到能够满足终端弹道倾角和法向过载约束要求的末制导律。本文制导律的设计不需要线性化,对多个终端约束逐阶设计来满足要求。在存在多扰动情况下的仿真结果显示制导律有很好的制导精度,具有一定的鲁棒性。同时本文给出的制导方案预留一段近似平飞段,该段可以用于减速控制。
[1] Kim M,Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1973,9(6):852-859.
[2] Kim B S,Lee J G,Han H S.Biased PND law for impact with angular constraint[J].Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
[3] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科学技术大学出版社,1997:214-230.
[4] Slotine J E,Li W.应用非线性控制[M].程代展,译.北京:机械工业出版社,2006:173-176.
[5] 贾庆忠,刘永善,刘藻珍.电视制导侵彻炸弹落角约束变结构反演制导律设计[J].宇航学报,2008,29(1):208-214.
[6] Harl N,Balakrishnan SN.Reentry terminal guidance through sliding mode control[J].AIAA Journal of Guidance,Control,and Dynamics,2010,33(1):186-199.
[7] 康佳仁.潘兴-2精确末制导技术分析[J].导弹与航天运载技术,1991(12):45-61.
[8] Zarchan P.Tactical and strategic missile guidance[M].Progress in Aeronautics and Astronautics,AIAA,Reston,VA,2012:569-601.

