基于Matlab和Solidworks的水轮机叶片设计和三维建模*

宋文龙 刘湘晨 周 晓 董俊杰 张馨玉

(1. 北京化工大学机电工程学院；2. 北京石油化工学院机械工程学院)

基于Matlab和Solidworks的水轮机叶片设计和三维建模*

宋文龙**1刘湘晨2周 晓2董俊杰2张馨玉2

(1. 北京化工大学机电工程学院；2. 北京石油化工学院机械工程学院)

以100kW水轮机为例，依据Wilson叶片设计原理，运用Matlab编程实现其算法；然后利用函数拟合对算法运行结果进行线性修正，并对修正前后的结果作了对比；最后根据点的坐标理论将翼型剖面二维坐标转化为空间实际坐标，并利用Solidworks进行叶片的三维实体建模，为后期的数值模拟和强度校核奠定基础。

水轮机 叶片 Wilson设计法 三维建模

能源短缺是制约我国经济发展的重要因素，寻求新能源和合理开发利用现有能源已成为目前的研究热点。近年来，海洋资源也因其丰富的能源蕴藏得到了广泛的关注，越来越多的专家学者将目光转向了海洋能源的开发利用[1]。其中，利用水平轴海流能发电的水轮机作为新型可再生能源的载体，已得到许多专家和学者的认可。

叶片是水轮机将海流能转化为机械能的核心部件，叶片参数直接影响水轮机整个发电机组的效率，因此叶片设计是水轮机设计的首要部分。笔者以100kW水轮机为例，依据Wilson叶片设计原理。基于Matlab和Solidworks对水轮机叶片进行设计和三维建模。

1 水轮机叶片的设计

1.1叶片设计参数

水轮机叶片设计主要是根据水轮机的已知设计参数来完成叶片半径R的确定、叶片剖面翼型的选取和各叶素弦长L、安装角β的确定。水轮机的已知设计参数如下：

额定功率P100kW

能量系数Cp0.35

水流速度V1.2m/s

水轮机传动效率η0.85

海水密度ρ1 025kg/m3

尖速比λ8

叶片数B3片

1.2叶片半径R的确定

水轮机叶片半径R的计算式为：

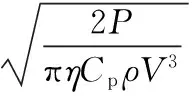
(1)

经计算得水轮机叶片半径R为10.42m，近似取为10.5m。

1.3叶片剖面翼型的选取

水轮机获能的主要结构是叶片，而叶片设计的关键在于翼型的选择。为了满足水轮机特性，笔者参考英国南安普顿大学水轮机翼型，选取 NACA63-8XX系列翼型。NACA63-8XX系列翼型具有较宽的升力系数运行空间，能够有效延迟失速分离，具有良好的变工况特性，且其具有较大的翼剖面弯度，在特定的攻角范围内可以具有较大的升力系数，增加周期输出功率[2]。

1.4叶素弦长L和安装角β的确定

风力机设计普遍采用Glauelt 设计法和Wilson设计法。Glauelt 设计法忽略了翼型阻力和叶尖损失的影响，但由于叶尖处的叶素受力对整个风机性能影响很大，因此叶尖损失不可忽视；而Wilson设计法对Glauelt设计法作了改进，综合考虑了叶尖损失和升阻比对叶片最佳性能的影响，以使每个叶素的能量系数达到最大，从而使整个叶轮的能量系数最大化，这一改进使得Wilson设计法应用范围更加广泛。笔者就是基于Wilson设计法的进行水轮机叶片设计，同时考虑到升阻比对轴向和周向诱导因子的影响较小，故在外形设计时不计阻力影响，使设计简化。

2 Matlab 编程实现Wilson设计法

2.1Wilson设计法

Wilson设计法的数学模型为：

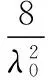
(2)

a(1-aF)=b(1+b)λ2

(3)

(4)

(5)

(6)

(7)

β=φ-α

(8)

式中a——轴向诱导因子；

b——周向诱导因子；

CL——升力系数；

F——普朗特修正因子；

r——叶素剖面到风轮中心的距离；

α——叶素攻角；

φ——叶素倾角。

Wilson设计法的具体实现步骤为：

a. 设定常量和相关设计参数；

b. 计算叶轮半径R，根据叶素动量理论，将叶片沿展向平均分成15等份，把每个叶素截面当作计算单元；

c. 以式(2)为目标函数，式(3)为约束函数，求解最优化问题得到每个叶素截面处的轴向诱导因子a、周向诱导因子b和普朗特修正系数F；

d. 求解实际工作条件下的雷诺数Re，从而求得最佳升阻比对应的攻角α和相对应的升力系数CL；

e. 计算每个叶素截面处的倾角φ，并根据式(8)得出相对应叶素截面处的安装角β；

f. 计算每个叶素截面的弦长L；

g. 对得到的叶片各叶素弦长L和安装角β进行线性修正，以满足加工及结构等方面的要求；

h. 查阅翼型手册确定翼型数据，并计算各叶素截面的翼型坐标。

2.2利用Matlab软件编程来实现Wilson设计法

根据Wilson设计法编制叶片的设计程序，将筛选出的各翼型分别输入程序，得到各翼型设计的叶片各叶素弦长L和安装角β，具体框图如图1所示。

图1 Wilson算法流程框图

Matlab实现该过程的难点在于诱导因子a和b的求解。运用Matlab最优化工具箱中的Fmincon函数可以有效求解非线性等式或不等式的约束问题。本问题是求解水轮机叶片能量系数Cp的最大值，但Fmincon函数只能求解最小值，故在式(2)等号右边加上负号，即：

(9)

将求解a及b等参数的主函数程序放入M文件中，命名为main.m，同时再创建两个命名为myjob.m和mycon.m的M文件，分别存放目标函数和约束函数。在迭代求解a、b时需要对a、b赋初值，a、b的初值经验公式为：

(10)

b=10/(λ0e12r/R)

(11)

在实际运算中，发现对a、b赋初值0完全可以满足运算要求。

2.3程序运行结果的修正

通过迭代计算得出的叶素弦长L和安装角β保证了每个叶素的捕能效率最大化，使每个叶素截面都能按照近似理想状态运行。但在这种思路下设计的叶片，在轮毂附近导致弦长L和安装角β较大，增大生产和加工难度。为解决此问题，需要对计算所得的弦长L和安装角β进行线性修正。根据文献，水轮机捕获能效的75%是由叶片前半部分产生，因此对叶片翼展方向0.6R～0.9R进行线性拟合，运用Matlab中ploy函数对弦长L和安装角β进行4次拟合，拟合多项式为：

L(r)=q1r4+q2r3+q3r2+q4r+q5

(12)

β(r)=q1r4+q2r3+q3r2+q4r+q5

(13)

求出对应的q1～q5代入式(12)、(13)，形成以r为自变量，L和β为因变量的函数。将0.1R～1.0R截面各叶素的r带入式(12)、(13)，分别求出修正后的叶素弦长L和安装角β(表1)。对比修正前、后的叶素弦长L和安装角β，发现叶根处的叶素弦长L和安装角β明显降低，这样既节省了材料，也更易于加工。

表1 各叶素参数修正前、后对比

3 叶片各截面空间坐标变换

通过空间坐标变换可以将翼型的二维坐标转化为实际建模所用的三维坐标[3]。具体步骤为：

a. 从profili或naca翼型库获得原始翼型数据(x0，y0)。

b. 求解以翼型气动中心为原点，翼弦方向为理想轴的二维坐标(x1，y1)。通常气动中心至翼型前缘的距离取 0.25L～0.35L，取 0.3L为气动中心的x轴坐标，y轴坐标为0，设气动中心坐标为(x3，y3)，故(x1，y1)=(x0，y0)-(x3，y3)。

c. 求解翼型空间三维坐标。

翼型空间三维坐标为：

(14)

使用Excel软件根据式(14)求得各叶素的空间三维坐标(x，y，z)，并保存为文本文档，以便后续三维建模使用。

4 叶片的三维实体建模

根据计算得出的叶素截面空间三维坐标(x，y，z)，通过CAD/CAM软件进行建模。笔者采用Solidworks软件来完成叶片的三维建模，具体步骤为：

a. 绘制叶素轮廓线。利用 Solidworks的“通过xyz曲线”命令输入各叶素的空间坐标，绘制每个叶素翼型的上、下弦，即可得叶素轮廓线。

b. 生成叶素平面。利用“平面区域”命令将叶素轮廓线填充为平面。

c. 结合叶柄数据，生成叶片实体。利用“曲面放样”命令实现在各叶素面间放样生成立体图(图2)。

a. 修正前

b. 修正后

5 结束语

笔者以100kW水轮机为例，结合Matlab编程软件，运用Wilson设计法对水轮机叶片进行了外形设计；然后根据空间坐标变换理论，运用Excel软件将翼型的二维坐标转化为实际空间三维坐标；最后应用Solidworks软件对叶片进行三维实体建模。笔者所使用的一整套水轮机叶片建模方法极大地缩短了复杂曲面的建模时间，易于操作，实用性强，为进一步对叶片进行数值模拟和强度校核奠定基础。

[1] 戴军，单忠德，王西峰，等.潮流发电技术的发展现状及趋势[J].能源技术，2010，31(1)：37～41.

[2] Bahaj A S, Molland A F, Chaplin J R, et al. Power and Thrust Measurements of Marine Current Turbines under Various Hydrodynamic Flow Conditions in a Cavitation Tunnel and a Towing Tank[J].Renewable Energy, 2007, 32(3): 407～426.

[3] 张礼达，任腊春，陈荣盛，等. 风力机叶片外形设计及三维实体建模研究[J].太阳能学报，2008，29(9)：1177～1180.

TurbineBladeDesignand3DModelingBasedonMatlabandSolidworks

SONG Wen-long1, LIU Xiang-chen2, ZHOU Xiao2, DONG Jun-jie2, ZHANG Xin-yu2

(1.CollegeofMechanicalandElectricalEngineering,BeijingUniversityofChemicalTechnology,Beijing100029,China;2.CollegeofMechanicalEngineering,BeijingInstitudeofPetrochemicalTechnology,Beijing102617,China)

Taking a 100kW water turbine as an example,the Wilson design method-based mathematical model for the blade shape parameters were obtained and the blade’s design program were written with Matlab. Having the results corrected through function fitting and compared with that before corrected, and then basing on the space coordinate transform theory, having airfoil-type two-dimensional geometry coordinate transformed into the space three-dimensional coordinates and making use of Solidworks software establish a 3D model for the blades.

water turbine, blade, Wilson design method, 3D modeling

*北京市教委科技计划项目资助(KM201310017003)。

**宋文龙，男，1988年10月生，硕士研究生。北京市，102607。

TQ051.21

A

0254-6094(2015)01-0093-04

2014-04-25，

2015-01-15)