感应式磁悬浮球形主动关节的模糊神经网络控制研究

曾　励，陈秋月，张小红

(扬州大学 机械工程学院，江苏 扬州　225127)

感应式磁悬浮球形主动关节的模糊神经网络控制研究

曾励，陈秋月，张小红

(扬州大学 机械工程学院，江苏 扬州225127)

摘要：磁悬浮球形主动关节机械集成度高，在控制和轨迹规划方面占有优势.文章提出基于模糊神经网络控制的感应式磁悬浮球形主动关节系统，建立了三维电机电磁功率平衡关系的电磁转矩和电磁悬浮力模型；基于模糊神经网络逆系统对电机进行多变量耦合关系解耦控制，建立关节系统的ANFIS模型，并对关节控制系统进行了系统仿真分析和实验研究.

关键词：感应式球形主动关节；电磁转矩；电磁悬浮力；模糊神经网络

传统多自由度旋转机械系统由多台单自由度电机及复杂的机械传动机构组成，以实现空间的多自由度运动.该类系统存在结构复杂、体积大、各关节摩擦面磨损严重、效率低，精度不够、响应缓慢、动态性能较差等问题[1-2].作为一个研究的切入点，本文提出并设计制造了感应式磁悬浮球形主动关节系统来代替传统的多自由度旋转机械系统，不仅能简化机构的复杂度、缩小机构体积，而且能够实现关节转子与定子之间无摩擦、无磨损的悬浮支承，提高关节的定位精度和响应速度，达到快速响应的目的.

感应磁悬浮球形主动关节是强耦合非线性系统，若采用传统的PID控制策略，当系统受到较大扰动时，由于整定参数固定不变，容易出现积分饱和而不能达到控制需求[3-4].采用模型参考自适应控制、平滑模型控制等方法，可以提高系统的性能，但必须依赖已知数学模型及模型的固定参数和结构.本文基于模糊神经网络逆对系统进行智能控制，利用神经网络的优点，将其与模糊逻辑有机结合产生自适应模糊神经网络，对系统进行模糊控制.内容包括对感应式磁悬浮球形主动关节进行机制研究[5]，建立关节的电磁悬浮力及电磁转矩模型[6-7]，以及关节球形转子的三维动力学非线性耦合模型，并构造了原关节系统的模糊神经网络逆系统，对关节悬浮和旋转特性进行控制和研究.

1感应式磁悬浮球形主动关节运行机制

图1　感应式球形主动关节三维造型

感应式磁悬浮球形主动关节的总体三维结构如图1所示.磁悬浮球形关节主要由正方体的壳体、6个结构上两两对称的定子、1个转子、5个电磁铁以及若干辅助零件组成.电磁铁与尼龙缓冲圈连接，尼龙缓冲圈的球面与转子球面的距离靠电磁铁螺纹连接进行调节，尼龙缓冲圈的动作取决于电磁铁的得电与失电.当球形关节未启动时，电磁铁处于得电状态，电磁铁的推杆伸长驱动尼龙缓冲圈夹持住球形转子，使转子处于悬浮中心，当球形关节得电启动时，电磁铁失电，电磁铁推杆收缩，此时转子被松开，转子处于工作时的悬浮状态.

图2是关节定子和转子的结构图.定子为4极12槽，如图2(a)所示.定子材料选用硅钢DW465-50.转子如图2(c)所示，类似单自由度感应电机的鼠笼转子，称为球笼转子.即转子表面均匀分布有类似球状鸟笼结构且相互短接的圆弧状电枢导条，从转子中心(球心)到球面的圆弧状电枢导条，均匀分布着放射状的短路电枢导条，以构成感应式关节转子的电枢绕组.

图2　定子和转子结构

当关节的某方向一组定子的线圈通入三相交流电时，类似普通单自由度电动机，关节定子绕组为球形转子提供绕该定子绕组中心线方向的旋转磁场，球形转子的电枢绕组在旋转磁场内做切割磁力线运动，产生感应电动势，进而在转子绕组中形成感应电流，在定子旋转磁场和转子感应磁场的相互作用下，产生感应式磁悬浮球形主动关节的电磁转矩，驱动关节转子沿定子电枢绕组中心线旋转；在控制系统作用下，通过调节关节某径向方向球形转子两侧对称的定子绕组电流大小，使球形转子在该方向上受到的径向电磁力随之变化，以保持磁悬浮球形主动关节的径向稳定悬浮.

2感应式磁悬浮球形主动关节的数学模型

2.1　关节悬浮力和电磁转矩模型

模糊神经网络逆系统解耦，是基于感应式磁悬浮球形主动关节电磁悬浮力和电磁转矩的数学模型，求解输出和输入的关系，为模糊神经网络逆系统的训练提供合理的输入和输出训练数据.

2.1.1磁悬浮球形感应电动机的电磁模型

图3　绕组空间分布

根据感应式球形主动关节的结构，定子内球面上分布有6个正弦绕组，分别为wx1、wx2、wy1、wy2、wz1、wz2.其中，wx1和wx2的轴线与空间静止坐标系的x轴重合；wy1和wy2的轴线与y轴重合；wz1,wz2的轴线与z轴重合，见图3.

在定子静止坐标系x、y、z下，建立磁悬浮球形关节定子和转子绕组的电压平衡方程：

(1)

式中:rxs1、rxs2、rys1、rys2、rzs1、rzs2分别是6个定子绕组的电阻，ψxs1、ψxs2、ψys1、ψys2、ψzs1、ψzs2分别是各个绕组的磁链，d为微分算子d/dt.

在转子坐标系d、q、p下，建立转子电压方程：

(2)

式中：转子绕组导条呈对称分布并且电阻相等，用rr表示；ψdr、ψqr、ψpr分别为转子磁链.

将式(2)经过坐标变换后可得到转子在静止坐标系中的电压平衡方程：

(3)

式中：ωx、ωy、ωz是转子角速度在x、y、z轴线上的分量，ψxr、ψyr、ψzr是转子等效绕组的磁链.

在坐标系x、y、z下定子和转子绕组的磁链方程为

(4)

式中：Lx1、Lx2、Ly1、Ly2、Lz1、Lz2为6个定子绕组与转子绕组的互感；Lx为Lx1、Lx2的叠加，Ly是Ly1、Ly2的叠加，Lz为Lz1、Lz2的叠加；Lxs1、Lxs2、Lys1、Lys2、Lzs1、Lzs2为定子绕组的自感；Lxr、Lyr、Lzr为转子绕组自感.

电感均为常数，假定Lx=Ly=Lz，Lxr=Lyr=Lzr，Lxs=Lys=Lzs，将式(4)代入式(1)和式(3)，可以得到以定子电流和转子角速度为变量的电压平衡方程，其矢量表示为

,

(5)

2.1.2关节电磁转矩方程

(6)

式中:i1、i2、i3、i4、i5、i6分别为磁悬浮球形关节6个定子上的电流.

由式(6)可以看出，感应式磁悬浮球形主动关节的电磁转矩不仅含有3个坐标轴转矩分量，而且3个转矩分量与定子和转子电流之间存在复杂的耦合关系.

2.1.3关节电磁悬浮力方程

根据磁能的定义得感应式磁悬浮球形主动关节磁能为

,

(7)

根据机电能量转换原理，可得到感应式球形主动关节的电磁悬浮力模型为

,

(8)

式中ρ为转子对于定子的径向位移.

计算感应式磁悬浮球形关节的6个定子磁能，并将其进行叠加，可得到感应式磁悬浮球形主动关节的总磁能方程：

(9)

由此可得在静止坐标系下x、y、z3个坐标轴方向的电磁悬浮力为

(10)

由式(10)可知，感应式磁悬浮球形主动关节的电磁悬浮力，不仅含有3个坐标轴悬浮力分量，而且3个悬浮力分量与定子和转子电流之间也存在复杂的耦合关系.

2.2　关节的动力学方程和状态方程

感应式磁悬浮球形主动关节的球形转子在旋转和悬浮时，是具有6个自由度的自由刚体.参考文献[8]已给出感应式磁悬浮球形主动关节的动力学方程和状态方程.假设转子坐标系3个轴的转动惯量相等并且没有外加负载.则按照拉格朗日动力学原理，推导出转子旋转和悬浮的动力学方程为

(11)

将式(11)转换为磁悬浮球形主动关节的状态方程为

(12)

其输出方程为

Y=X1,

(13)

式中

.

根据逆系统解耦原理[10]分析可知，磁悬浮球形主动关节存在逆系统.根据上述的模型式(12)、(13)，只需要利用模糊神经网络构造出感应式球形主动关节的逆系统模型便可实现关节的线性化解耦.由输出方程Y=X1得

,

(14)

逆系统可表示为

,

(15)

基于式(14)、(15)两方程可对其进行闭环鲁棒控制.

3磁悬浮球形主动关节的模糊神经网络系统

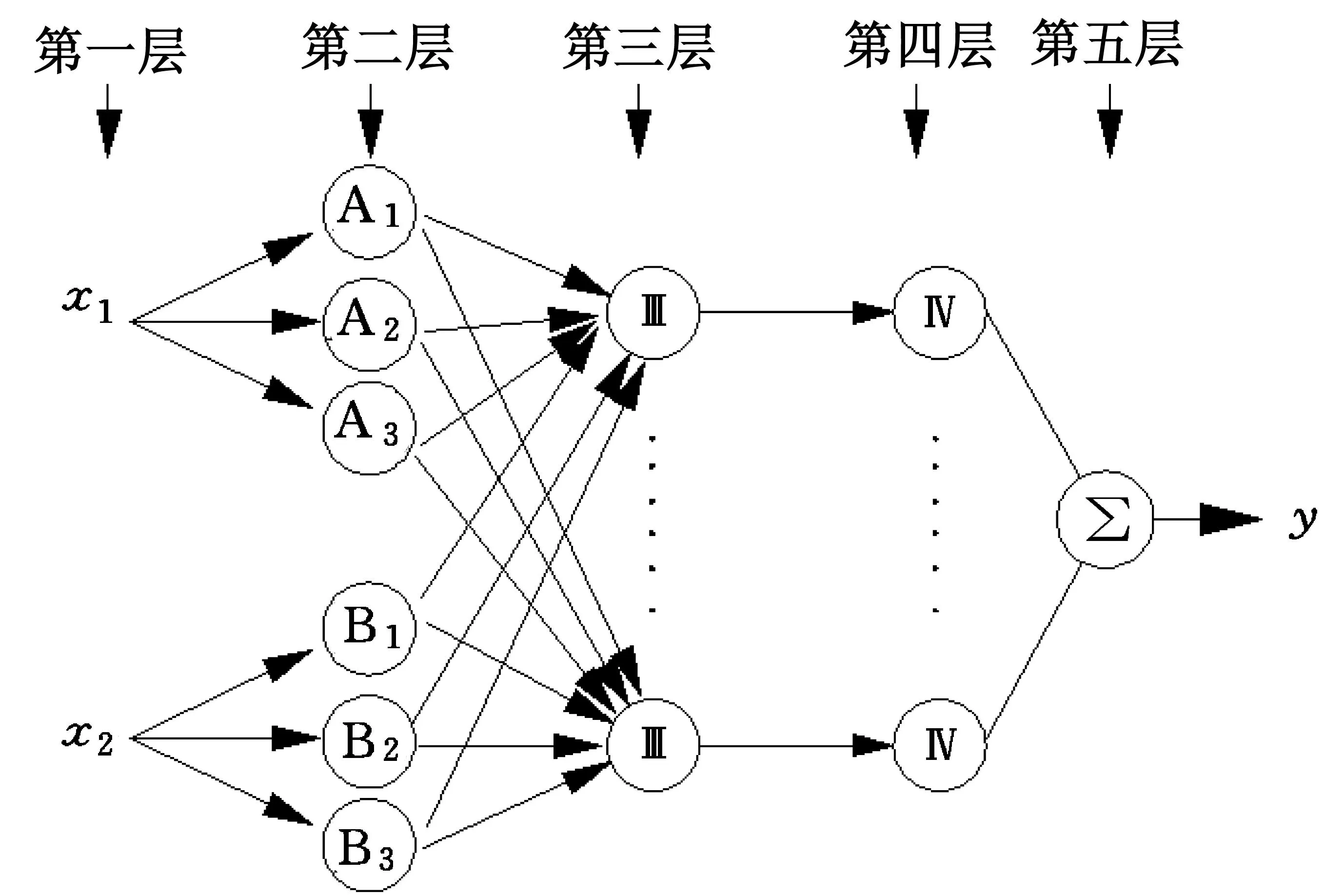
图4　基于一阶Sugeno模型的ANFIS结构

为便于对感应式磁悬浮球形主动关节系统进行解耦、闭环控制，建立自适应神经模糊推理系统(ANFIS)，通过给定的输入输出数据集，构建FIS模糊推理系统，与隶属度函数相关的参数将通过学习过程来改变，ANFIS或者单独使用反向传播算法，或者结合最小二乘法一起进行隶属度函数参数的预测和优化.

基于一阶Sugeno模型的ANFIS结构如图4所示.

图中，x1和x2是网络的输入，y为网络的输出.每层功能相似，其模糊规则库的组成如下：

ifx1isA1andx2isB1theny=p1x1+q1x2+r1,

2x1+q2x2+r2.

网络由5层构成，第1层为网络的输入层，输入结点是线性的，由2个神经元组成，将网络的输入信号x=[x1,x2]T传送到下一层中.

第2层为网络的隐含层，即该层各输入分量属于语言变量值模糊集的隶属度函数可选择高斯型函数，即：

,

(16)

式中：cij和σij分别表示隶属度函数的中心和宽度；i=1,2,…,n;j=1,2,…,mi;n是输入量维数2，即向量[x1,x2]T的维数为2；mi为输入量的模糊分割数3，即图4中的A1-A3或B1-B3.

第3层为模糊规则层，该层的结点总数为N3=m.每一个结点代表一条模糊规则，用来匹配模糊规则的前件，计算出每条规则的适用度,即

,

(17)

对于给定的输入变量，在输入点附近的语言变量值存在最大隶属度值，而远离输入点的语言变量值的隶属度很小甚至为0，当隶属度小于0.05时可近似取为0.

第4层为归一层.进行各条规则适用度的归一化计算，其节点数与第3层的节点数相同，即N4=N3=m，归一化计算可由下式计算：

/(j=1,2,…,m).

(18)

第5层是后件网络，用于计算每一条规则后件，即

,

(19)

式中j=1,2,…,m.

系统的输出为

.

(20)

可见，系统输出v是各规则后件加权和，其加权系数就是各模糊规则归一化的适用度，亦前件网络的输出用作后件网络的连接权值.

如果各输入分量的模糊分割数是预先确定的，则需要学习的参数主要是后件网络的连接权pji(j=1,2,…,m;i=1,2,…,n)，以及前件网络各结点隶属度函数中心值Cji(j=1,2,…,m;i=1,2,…,n)和宽度σji(j=1,2,…,m;i=1,2,…,n).

自适应模糊神经网络推理系统不仅具有模糊系统中无需知道被控对象精确模型和抗干扰性强的优点，又具有神经网络自学习和较高控制精度的优点，用它来构造复杂非线性耦合关节系统的逆系统，将构造出高性能并精确的逆系统.

由于感应式磁悬浮球形主动关节的3个自由度为独立控制，即可建立3个独立的控制子系统.本文只构造并分析关节系统在1个自由度方向的ANFIS逆系统.以x方向位移控制为例，则输入量为位移误差Δx和位移误差的变化率Δx′，选择模糊子集为7，隶属函数为高斯型函数，允许误差为10-3，训练次数为1500，输入数据包括定子输入电流和电流的变化率，输出数据包括定子绕组在静止坐标系u，q轴上的电流分量.输入、输出数据在磁悬浮球形主动关节的仿真实验中获得.

针对系统的不可预测性，选取功能较强的二型二阶滤波器为

(21)

λ可以在实验和仿真的条件下选取，以达到理想的鲁棒性能.其系统的鲁棒控制器可以表示为

,

(22)

式中a2、a1、a0为常数，同样可以在实验和仿真的条件下选取，以达到理想的鲁棒性能.

4仿真结果及实验研究

感应式磁悬浮球形主动关节样机的参数为：f=50 Hz,Rs=2.3 Ω,Rr=1.2 Ω,J=5.8×10-4kg·m2,Lxs=Lys=Lzs=0.573 H,Lxr=Lyr=Lzr=0.58 H,Lx=Ly=Lz=0.55 H,U=380 V.基于以上数据对感应式磁悬浮球形关节系统进行PID闭环控制仿真，进行6次数据采集，其中3次是在系统的3个转速输入端施加幅值在区间[0,50]rad/s的随机转速信号，另外3次是在系统的位移输入端施加幅值在区间[-0.2,0.2]mm的随机位移信号.由此得到模糊神经网络ANFIS逆模型的6组训练样本，每组仿真时间为200 s,获取仿真数据2000组，然后选择范围内的200个输入和输出数据对，将6组数据对规范化后作为ANFIS的训练样本，随机选择采样周期为2 ms时输入输出数据中的50个作为校验样本，用于检验ANFIS的泛化性能和判断是否出现过拟合.图5为ANFIS模糊神经网络与关节系统复合的伪线性子系统结构图.

图5　模糊神经网络复合伪线性系统

感应式球形主动关节在空载状态下，转子在静止坐标系下x、y方向的初始位置分别为0、0，而由于转子静止时是停靠在z轴负方向的定子上，故z方向的初始位置为-200 μm，仿真时间设定为1.2 s，负载转矩为T=0.

为了看出本文控制系统设计的优越性，分别用PID控制与模糊神经网络逆鲁棒控制两种方法，比较它们的转速响应和z方向位移响应.图6中比较可以看出，采用模糊神经网络逆鲁棒控制时，超调量很小，而且响应更快,0.3 s就能达到给定转速.

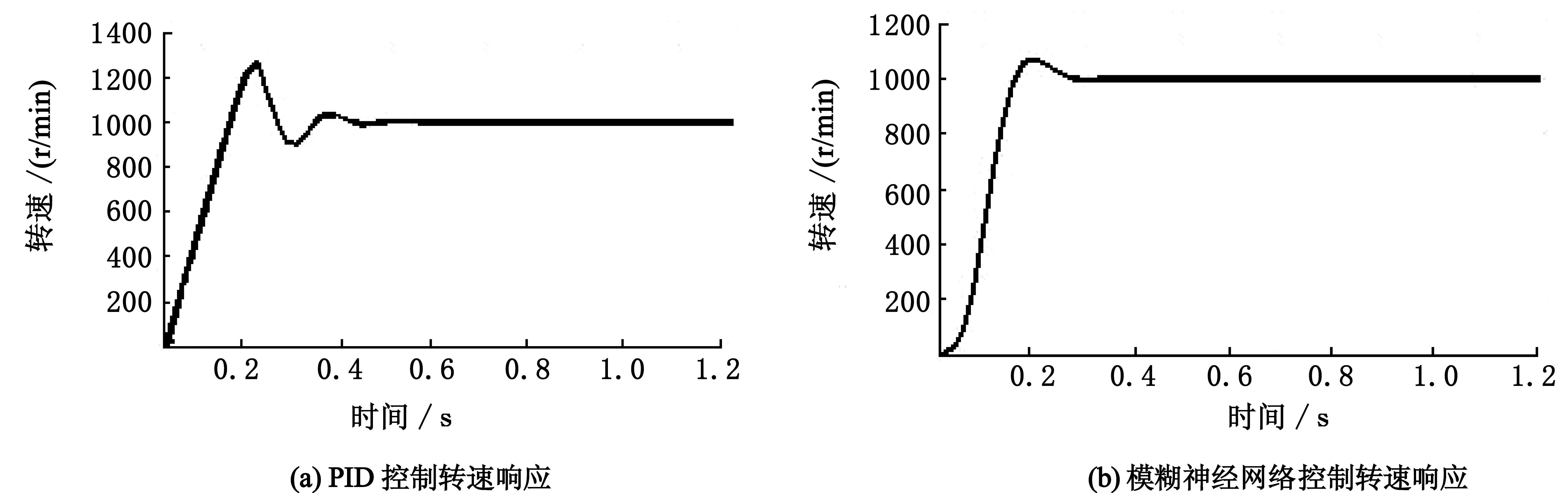
图6　转速响应曲线

从图7中的位移响应的比较可以看出，在关节稳定运转后，模糊神经网络逆鲁棒控制方法，转子在径向位置的偏移很小，响应过程中最大超调量小于50 μm，大概0.5 s时转子稳定到z轴方向的平衡位置.

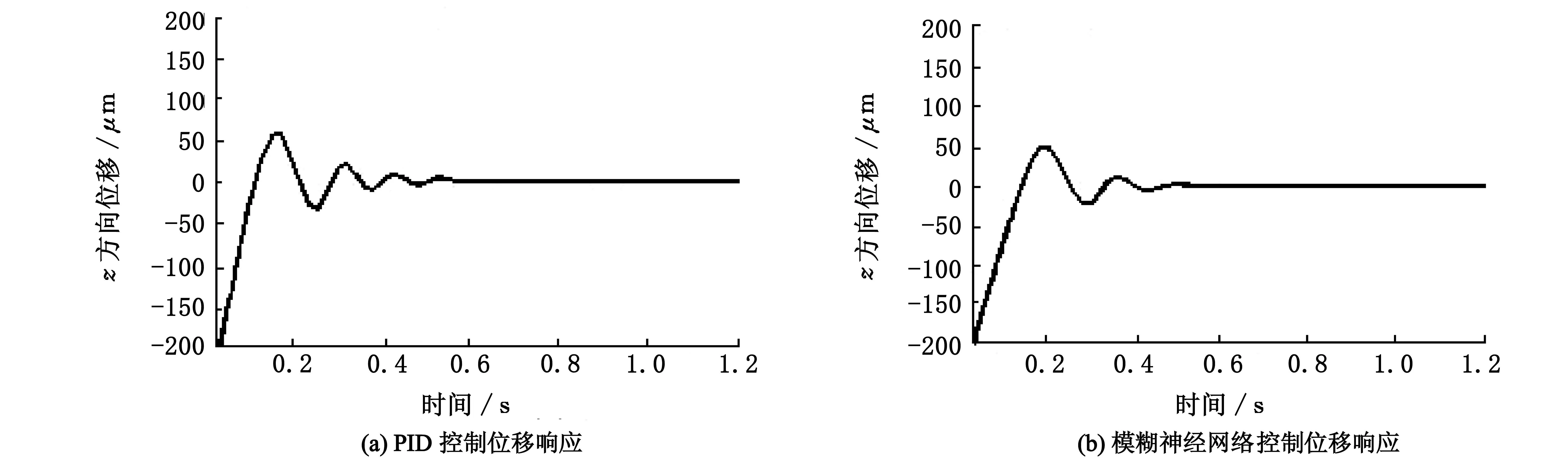
图7　z方向位移响应

图8为在t=0.6 s时，转速n突变为500 r/min时，模糊神经网络逆鲁棒控制方法转速跟踪曲线.可见转速突变后，模糊神经网络逆鲁棒控制能够很好地跟踪给定转速的变化，稳定误差小.转速响应快，0.3 s即可达到稳定转速，稳定运行后转速超调小于10 r/min，自适应能力强.而且稳定后转子的径向偏移小于2 μm,稳态误差很小，具有更强的鲁棒性稳定性.

基于本文所研究的模糊神经网络逆系统控制的结构，构建感应式磁悬浮球形主动关节的控制实验装置如图9所示.

图9　关节样机控制系统

图10为当给定转速为1000 r/min时球形关节的转速响应，在0.3 s时即可以达到稳定转速，超调量小于12%.图11为电磁转矩随转速的变化规律，随着转速的增大，转矩的波动慢慢变小，转速达到1000 r/min时，转矩变为0，但还有较小的波动.

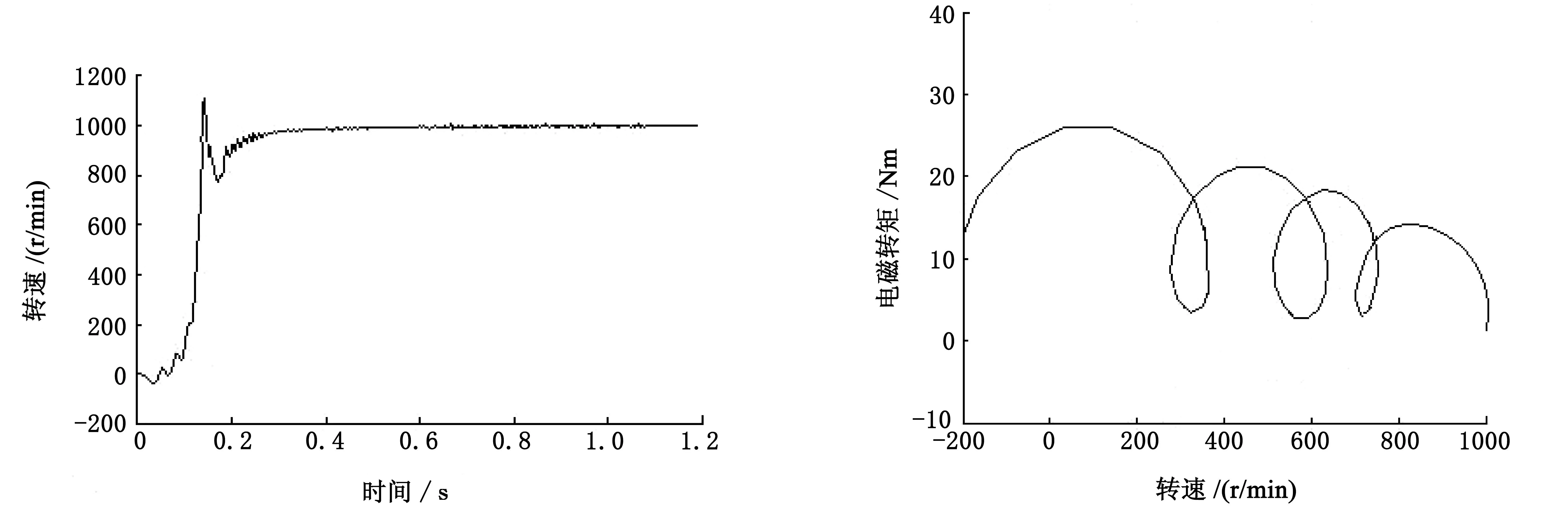
图10　给定转速1000 r/min时球形关节的转速响应　　　　　图11　电磁转矩随转速变化规律

图12为转子的位移响应，转子向下偏移的初始间隙为0.2 mm.在悬浮控制作用下，球形转子将移动到定子的中心位置，实现稳定悬浮.稳定悬浮时转子波动很微小.图13为球形转子上下启浮时加速度变化规律，可见在转子开始悬浮的0.4 s内，伴随着不停的微小振动，之后振动逐渐变为0.

图12　转子位移变化规律　　　　　　　　　　图13　位移加速度变化

5结论

1)利用ANFIS构造感应式球形主动关节系统的逆系统，其参数可以在学习的过程中获得，不需要原系统有明确的数学模型，只需要给出关节的输入和输出数据对其训练即可.

2)模糊神经网络逆系统在与原系统串联之后，即可将复杂非线性系统线性化，是一种非常方便快捷的线性化方法.

3)通过对比PID控制与模糊神经网络逆鲁棒控制两种方法，比较它们的转速响应和位移响应，本文提出的控制方法比PID方法响应快，稳定性高，适合在控制要求较高的场合使用.

4)基于控制结构建立了关节的实验装置，对感应式磁悬浮球形主动关节进行了转子位移特性和转速特性研究.

参考文献：

[1] 毛新涛,包钢,杨庆俊.3自由度气动串联机械手的关节控制[J].机械工程学报,2008.44(12):254-260.

[2] 李健,李剑锋,武祯.冗余度机器人多关节故障的运动学容错性及其优化[J].机械工程学报,2002,38(7):111-115.

[3] Hsu C F,Lee B K.FPGA-based adaptive PID control of a DC motor driver via sliding-mode approach[J].Expert Systems with Applications,2011,38(9):11866-11872.

[4] Hou B J,Gao J S,Li X Q,et al.Study on repetitive PID control of linear motor in wafer stage of lithography[J]. Procedia Engineering,2012,29(1):3863-3867.

[5] 曾励,王军,张丹.磁悬浮球形磁阻关节产生悬浮力和电磁转矩的机理分析[J].中国机械工程,2011,2(1):208-211.

[6] Zeng Li,Zhang Fan,Zhang Dan.Force and torque study of magnetic levitation spherical driving joint with magnetic field segmentation method[J].Przeglad Elektrotechniczny,2012,88(7B):235-238.

[7] Zhang Fan,Zeng Li,Chen Fang.Study of magnetic levitation spherical joint with decoupling control[J].Przeglad Elektrotechniczny,2012,88(7B):239-242.

[8] 曾励,张帆,徐媛媛.磁悬浮球形关节三维动力学模型与控制特性[J].中国机械工程,2011,47(21):69-74.

[9] 王军,曾励,张丹.多自由度磁悬浮球形主动关节机理及悬浮控制[J].机械设计与研究,2010(4):49-53.

[10] 李春文,苗原,冯元琨,等.非线性系统控制的逆系统方法(Ⅱ):多变量控制理论[J].控制与决策,1997,12(6):625-630.

[11] 陈庆伟,吕朝霞,胡维礼,等.基于逆系统方法的非线性内模控制[J].自动化学报,2002,28(5):715-721.

[12] 何丹,戴先中,王勤.神经网络广义逆系统控制[J].控制理论与应用,2002,19(1):34-40.

(编辑武峰)

中图分类号：TM352

文献标志码：A

文章编号：1674-358X(2015)03-0015-08

收稿日期：2015-03-13

基金项目：国家科技支撑计划项目(2013BAEL3B00)

作者简介：王庆良(1966-),男,江苏徐州人,教授,博士,硕士生导师，主要从事材料设计及摩擦学研究.

Internal Model Control of Inductive Magnetic Suspension Spherical Active Joints Based on Fuzzy Neural Network Inverse System ZENG Li,CHEN Qiuyue,ZHANG Xiaohong

(College of Mechanical Engineering, Yangzhou University, Yangzhou 225127, China)

Abstract:Maglev spherical initiative joints with high mechanical integrity are dominant in the control and trajectory planning.The article established the three dimensional electromagnetic model of electromagnetic torque and levitation force based on the inductive maglev spherical initiative joints system controlled by the fuzzy neural network and the ANFIS model of joints to decouple the multivariable coupling relationship based on the inverse system to the fuzzy neural network.The simulation analysis and experimental verification on the joint control system are also operated.

Key words:inductive spherical initiative joints; electromagnetic torque; electromagnetic levitation force; fuzzy neural network