天然气水合物分解动力学模型研究
雷昊 米洪刚 马勇新 戚志林 严文德
(1.中海石油(中国)有限公司湛江分公司,广东 湛江 524057;
(2.重庆科技学院复杂油气田勘探开发重庆市重点实验室,重庆 401331)
天然气水合物是21世纪的新能源,主要分布在深海沉积物或陆域永久冻土中,由天然气客体分子与水分子笼形晶格在高压低温条件下形成的类冰状的结晶物质。分子笼形晶格使用比各自笼子直径更小的弱极性客体分子来填充[1-3]。“本征动力学”主要是对天然气水合物分解动力学系统的“反应”进行系统研究[4-5],且参数变化由分解期间的搅拌速率、温度和压力共同影响。在超出一定搅拌速率的情况下对2种不同的动力学机制之间的变化进行观察,即天然气水合物的分解动力学。近些年,研究者对实验过程提出了改进,采用改进的模型对数据进行验证[6-10]。针对以上问题,研究者进行了分子动力学(MD)的甲烷水合物溶解过程模拟。结果发现,水合物的分解是一个非平衡的过程,故无法使用平衡热力学进行描述。
1 天然气水合物分解动力学模型
1.1 气体水合物模型
模型中涉及变量包括:气体水合物平衡压力p*,分解吸收的焓热量Δhβ-LOW,水和客体分子化学势μ[11-12]。在液态水存在的状态下,平衡条件如下:

文中,各变量的上标H表示水合物,上标L表示液态水,下标G表示客体分子,下标W表示水分子,下标O表示纯物质,上标β表示空水合物晶格,空水合物晶格的水化学位之差为ΔμβOW-L,客体分子晶体的水化学位之差为
通过以下方程组计算水在不同结构中变相的热质特性:
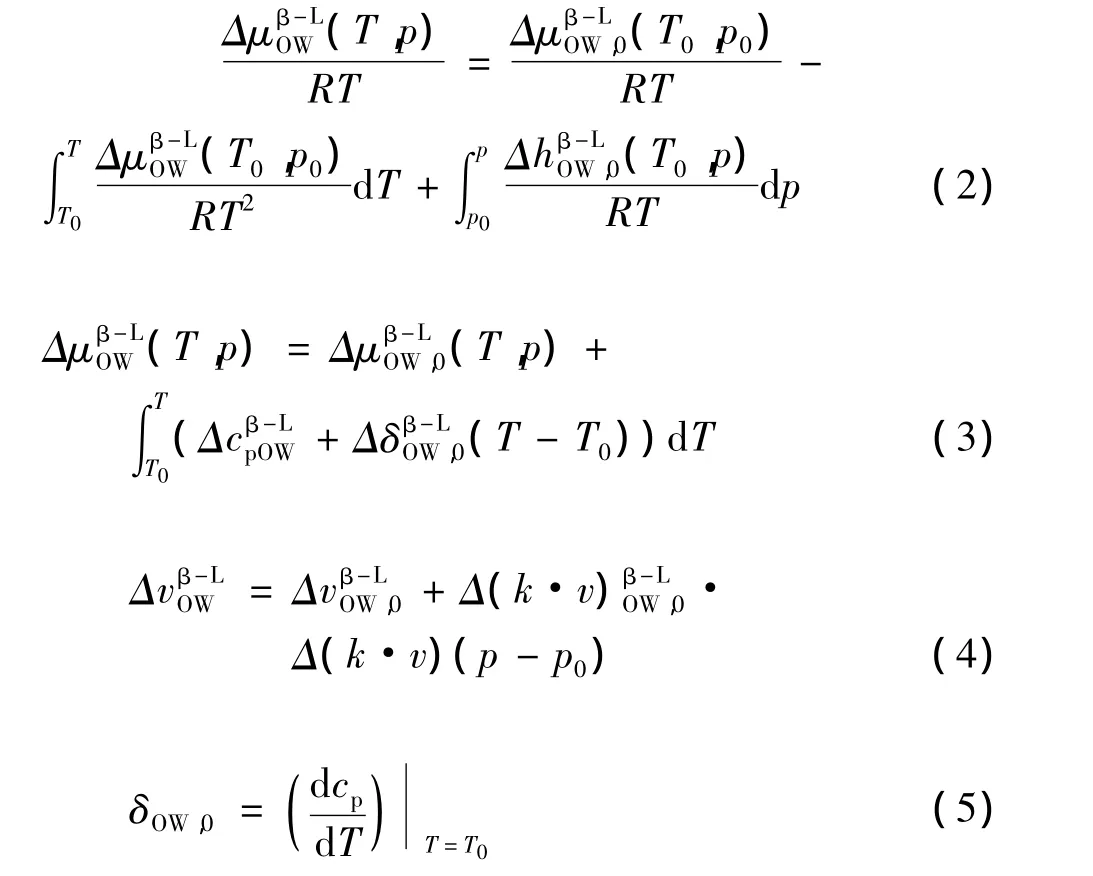
式中:h— 焓热量,J/mol;
cp— 等压热容,MPa-1;
δ—与温度相关的线性导数;
v— 容度,m3;
k—空水合物晶格的等温可压缩性,s-1。
T— 温度,K。
关于水合物相的化学势客体分子的贡献ΔμH-βW定义为:

式中:vi—不同孔穴类型的容度;θi—分子i的笼形空间占有率。
使用朗格缪尔系数Ci以及在平衡态下相应的气相逸度fG计算笼形空间占有率:

相对于径向坐标r,有式(8):


客体参数εi和笼格参数r0i的物理意义是中央井电位的饱和深度以及零交叉点的径向位置。根据依赖朗格缪尔系数理想的范特霍夫行为,确定了一个精确温度系数Ci:

式中Ci为水合物孔穴的朗格缪尔系数,MPa-1。
对温度的朗格缪尔系数的对数求导来计算客体分子的解吸焓热值,利用CWP,获得式(11):

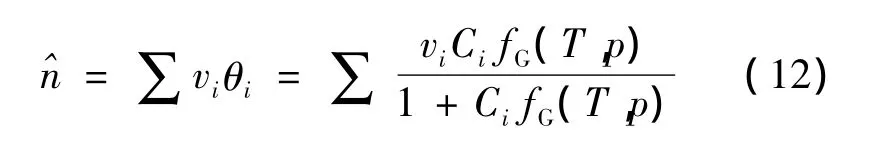
1.2 水合物相的几何特性
应用统计速率理论(statistial rate theory of interfacial transport,简称SRT)时需要用到客体分子的平均接触面积σG,其估计如下:

σi为第i类型孔穴内部的客体分子平均接触面积,根据分子i的笼形空间占有率θi及格子的化学计算系数vi,得到式(14):
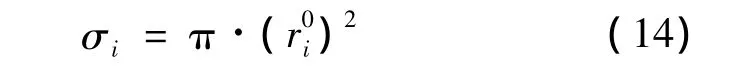
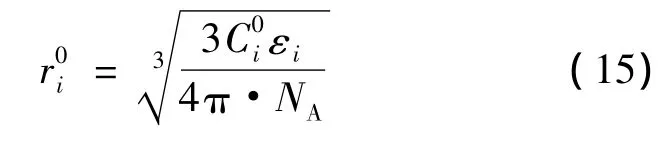
利用气水合物单元晶体内部水分子的数值~NUCW以及单元分子和格子体积vUCW(单元尺寸aUC孔穴直径 ri),得到 σW的表达式[14]。

1.3 状态方程式
根据使用马蒂亚斯和科普曼修正的能量参数的Redlich-Kwong-Soave状态方程,对yW是在假定理想的Raoult-Dalton行为下进行直接估计:
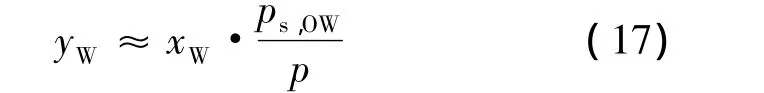
1.4 溶解度
假设vLG,∞为无限稀释的偏摩尔体积,水分子的客体溶解度xG的表达式如下:

要求使用状态方程计算气相逸度fvG,亨利系数HLG及参数 A,B,C:
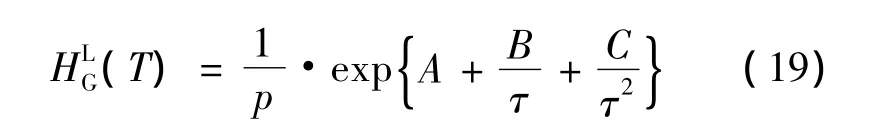
由于连续解析和溶解模型(consecutive desorption and melting model,简称CDM)在当前公式中是二元系统(水+1个客体分子),以下的表述是有效的:

1.5 扩散系数
为了得到依赖温度的扩散系数DL的正确描述,使用了来自于实验数据参数的阿列纽斯相关性。
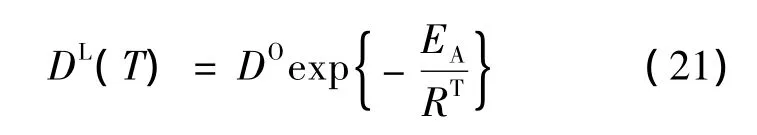
2 改进的天然气水合物分解动力学模型
2.1 模型基本思想和边界条件
CDM的基本思想是假设天然气水合物的分解局部连续,且是重复“反应”的分解过程,即:(1)一部分水笼客体分子在固体—流体界面解析;(2)空水笼是局部溶解。在固体—流体界面暴露出一个新的客体分子,并且过程将持续直到不稳定因素不存在或水合物完全分解。
模型理论推导的边界条件定义如下:(1)单个客体水合物(SI和SII);(2)没有外部热传质的限制;(3)等温分解过程。
CDM模型内采用上述分解过程的基本假设来估计分解动力学,同时使用碰撞频率模型描述和溶解动力学解吸来估计2个过程的动力学常数,对界面传递解吸过程的统计速率理论(SRT)[15]进行描述。
2.2 改进的模型
公式(22)阐述了固体水合物变为液态水和水分子客体的气水合物本征动力学,公式(23)阐述了固体水合物变为液态水以及在欠饱和环境溶解中的客体分子气水合物本征动力学。
分解(DC)方程

溶解(DL)方程为:

式中:σW—水的平均接触面积,m2;
σG— 客体分子平均接触面积,m2;
n˙ — 摩尔通量,mol/(s·m2);
DLW来估计;
DLG—水相内部客体分子的自扩散系数,m2/s;
ρW— 液体密度,mol/m3;
R— 通用气体常数,8.314 J/(mol·K);
x—液相质量分数,%,下标G、W分别代表客体分子和水分子;
y—气相质量分数,%,下标G、W分别代表客体分子和水分子;
ΔhβOW-L— 空晶体格焓热量变化,J/mol;
θG—气体分子的笼形空间占有率,%;
fG— 客体分子的液相逸度,Pa。
上式中,上标“*”表示对应的等温三相(水合物-液体-气体)平衡条件。
在条件限制下,˙NG为本征动力学的客体分子分解的总速率,可以利用整体几何水合物-流体界面AH-F乘法计算[16]:
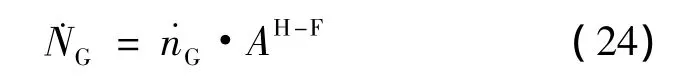
式(22)、(23)、(24)是关于动力学理论问题的一般描述。
3 CDM模型讨论
3.1 CDM模型的边界条件
在开始讨论CDM结果之前,先定义几个边界条件:(1)假设流体的压力和相应的组合物在分解过程中连续;(2)液体中具有游离流体;(3)水合物-流体边界层无传热和传质限制的理想搅拌釜式反应器特性。由于气水合物分解包含整个宏观驱动在气水合物-液态界面局部穿过分解边界层,进而产生了一个等温分解过程。
3.2 时间常数
通过特征时间常数给出了客体分子分解的单个速率常数,其值取自式(22)和(23)的反应常数和的倒数值:
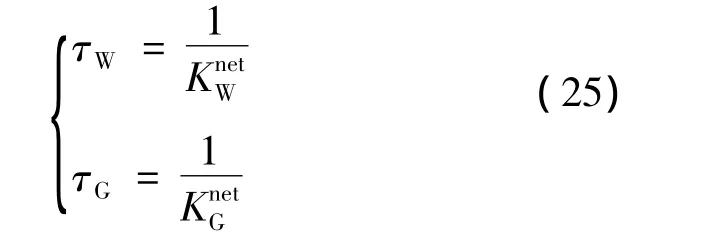
式中,τ是水分子从水合物到液态的时间改变测量值,通过观察得出利用解吸过程进入液态比各自解吸进入液态慢3个数量级;同样,空晶体格的溶解发生比解吸过程快几个数量级。
根据以上观点,认为水合物溶解过程比分解的过程更慢,即客体分子的解吸过程具有速率限制。
3.3 分子驱动势能ΔΘ
基于依赖温度的本征动力学分解,根据客体分子集聚逸度和平衡逸度fG、f*G来定义客体分子驱动势能ΔΘ理论。

不同温度的驱动势函数定义依赖于具体的气体释放速率。首先,随着温度的升高分解率出现升高趋势;其次,在溶解的过程中,线性趋势很明显,且随着驱动的增加,气体释放速率将会变慢。
3.4 分子反应速率常数kΘD
进一步讨论,分子反应速率常数kΘD用式(27)来定义:


使用客体分子在分解过程中的最大可能分解速率极限的测量值来解释速率常数,进一步讨论依赖于温度的分解反应。

式中,EA表示分解过程中活化能,ΔhH-βG是客体分子从满晶格笼到液相的分解焓热量值。
根据热力学观点,活化能是关于系统跨越化学势阻碍ΔμA-S>0的能量需求。自发反应进行的条件要求为ΔμF-A<0。对于ΔμA-S>0的热平衡叫做活化能,这里的热平衡是指反应热。
3.5 势函数
在实际应用中,通过直接引用驱动函数的手段来阐述实验性气水合物分解动力学,公式(31)阐述了2个随机的势函数ψ1和ψ2之间的关系:
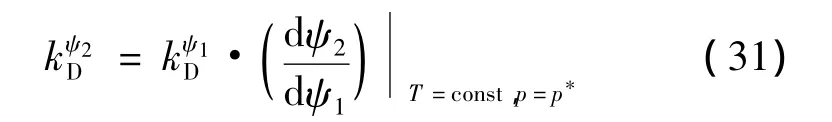
式中,微分项是关于ψ2— ψ1平面的 HLV平衡曲线的斜率。为了证明在动力学相变应用过程中,本征动力学是否起了重要作用,在实验过程中,它是通过全程观察记录固体被液体层润湿而成为游离气体水合物的过程。因此,物理过程在水合物-流体界面发生更类似于客体分子直接水合物-液态解吸的情况。
为了获得更接近本征动力学的实验数据,长度d采用液态水相DWG附近的内部分解速率常数KCG,以及客体分子扩散系数来定义:

在水合物-液态界面下,这个值等于本征动力学在限速情况下扩散边界层的厚度,d相当于本征动力学在限速情况下晶体直径。
4 CDM预测与MD模拟对比实例
对CDM预测与MD模拟结果进行对比,在290 K时,应用公式(23)与公式(24)进行CDM的预测。
在图1右边区域,当溶解客体的xG在接近饱和值290 K和15.96 MPa,即HLV的等温平衡点时,CDM模型的分解速率急剧降低。从图中可以看出,这是一种客体吸附控制的转变方法:(1)超过了转变范围;(2)水合物晶格熔化方法;(3)客体分子溶化随摩尔分数递减。
从结果看,在客体溶解的低摩尔分数下,CDM与MD模型的分解速率有很好的一致性,且2个模型的边界条件相似。
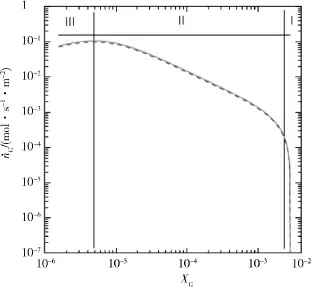
图1 CDM预测与MD模拟结果对比
5 结语
本次研究应用本征气体水合物分解动力学改进模型对天然气水合物成分的分解过程进行预测,结论如下:
(1)在相同驱动梯度条件下,天然气水合物的分解速度比各成分单独分解的速度相对更慢。
(2)用客体解吸驱动梯度和气水合物分解速率的上极限表示的水合物晶格熔解过程具有独立性,应用分子分解速率流标准化公式能得到不同水合物形式的分解速率常数。
(3)对客体分子的低浓度分解速率进行模型预测与MD模拟,结果显示出2个模型良好的一致性。
[1]Windmeier C,Oellrich L R.Theoretical Study of Gas Hydrate Decomposition Kinetics-Model Development[J].J.Phys.Chem.,2013,117:10151-10161.
[2]VysniauskusA,Bishnoi P R.A Kinetic Study of Methane Hydrate Formation[J].Chem.Eng.Sci.,1983,38(7):1061-1072.
[3]GuptaA.Methane Hydrate Dissociation Measurements and Modelling:the Role of Heat Transfer and Reaction Kinetics[G].Colorado School of Mines,2007:101-108.
[4]Kim H C.A Kinetic Study of Gas Hydrate Decomposition[D].Canada:University of Calgary,1985:1-25.
[5]Kim H C,Bishnoi P R,Heidemann R A,et al.Kinetics of Methane Hydrate Decomposition[J].Chem.Eng.Sci.,1987,42(7):1645-1653.
[6]Clarke M.Determination of the Intrinsic Kinetics of Gas Hydrate Decomposition by Particle-Size Analysis[D].Canada:University of Calgary,2000:1-50.
[7]Clarke M,BishnoiP R.Determination of the Intrinsic Rate of Ethane Gas Hydrate Decomposition[J].Chem.Eng.Sci.,2000,55(21):4869-4883.
[8]Clarke M,Bishnoi P R.Determination of the Activation Energy and Intrinsic Rate Constant of Methane Gas Hydrate Decomposition[J].Can.J.Chem.Eng.,2001,79(1):143-147.
[9]Clarke M,Bishnoi P R.Measuring and Modeling the Rate of Decomposition of Gas Hydrates Formed from Mixtures of Methane and Ethane[J].Chem.Eng.Sci.,2001,56(16):4715-4724.
[10]Clarke M,Bishnoi P R.Determination of the Intrinsic Rate Constant and Activation Energy of CO2Gas Hydrate Decomposition Using In-Situ Particle Size Analysis[J].Chem.Eng.Sci.,2004,59(14):2983-2993.
[11]Sloan E D,KohC A.Clathrate Hydrates of Natural Gases[M].3rd.CRC Press:Boca Raton,FL,2007:95-105.
[12]Makogon Y F,Dunlap W.Hydrates of Hydrocarbons[M].Tulsa:Pennwell Publishers,1997:1-30.
[13]Holder G D,Zetts S P,Pradhan N.Phase Behaviour in Systems Containing Clathrate Hydrates[J].Rev.Chem.Eng.,1988,5(1):1-70.
[14]BazantM Z,Trout B L.A Method to Extract Potentials from the Temperature Dependence of Langmuir Constants for Clathrate-Hydrates[J].Physica A,2001,300(1/2):139-173.
[15]Ward C A,Findlay R D,Rizk M.Statistical Rate Theory of Interfacial Transport.I.Theoretical Development[J].J.Chem.Phys.,1982,76(11):5599-5605.
[16]周锡堂,陶鲜花,庞重军.天然气水合物分解动力学研究进展[J].天然气化工,2006,31(5):70-73.

