风电场中基于核密度估计法的储能系统容量配置
宋志惠,许 玥
中国葛洲坝集团国际工程有限公司
风电场中基于核密度估计法的储能系统容量配置
宋志惠,许 玥
中国葛洲坝集团国际工程有限公司
前言
储能系统具有动态吸收能量并适时释放的特点,能有效弥补风电的间歇性、波动性缺点,改善风电场输出功率的可控性,提升稳定水平。在并网风电场中配置适量的储能系统,对风电场的输出功率进行调节,可提高风电场出力的可控性,使得风电场成为灵活可控的电源。
1 储能系统实时调节风电场输出功率以跟踪功率预测值
根据风电场的实际输出功率和电网给风电场下达的发电指令目标(功率预测值),储能系统通过充电或放电实现缩减或消除前两者偏差的目的。通过控制储能系统快速、精确的功率吞吐能力,可以调节风电场的实时出力平稳跟随发电指令目标,使得风电场像常规电场一样具有按照发电曲线运行的能力。
2 非参数核密度估计方法
参数估计是假定数据总体的分布类型已知的情况下对参数的估计,参数确定则概率密度完全确定,但实际中很多数据的分布类型是无法事先假定的。
核密度估计是非参数估计类型的一种,它可以很好的描述连续的密度函数。其定义:对于数据x1,…,xn,核密度估计有如下形式:
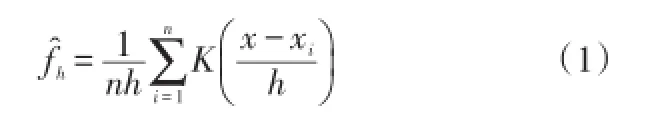
这是一个加权平均,而核函数K(·)是一个权函数。核函数的形状和值域控制着用来估计f(x)在点x的值时所用数据点的个数和利用的程度。
带宽的大小对估计量有很大的影响,小的带宽会将密度分配得太局限于观测数据附近,导致估计密度函数有很多错误的峰值;而大的带宽会将密度贡献分布得太开,从而会因光滑而遗失掉的一些特征。选择合适的带宽需要相应的评价标准,渐进积分均方误差(AMISE)计算公式如下:
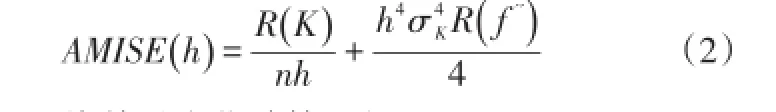
将其最小化计算可得:
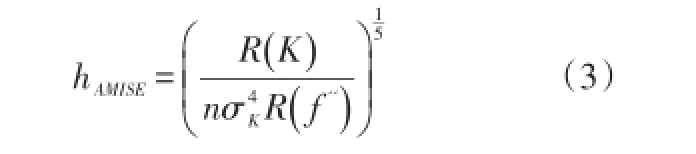
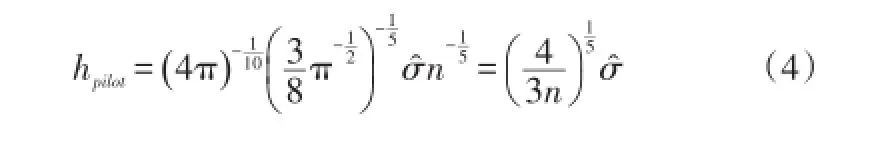
3 储能系统容量的确定
在一段时间内,储能系统功率在时间上的积分即可得到储能系统能量的变化。为了确定储能系统的容量,取一天内能量的最大值的绝对值,记作||Emax,记录250天的数据曲线。对其进行概率统计,并用核密度估计法估计概率密度函数,具体为图1所示。
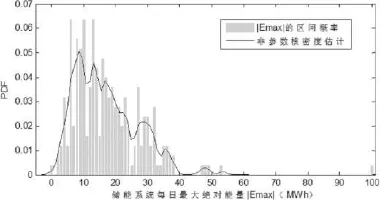
图1 ||Emax的概率密度函数
上图中核密度函数为高斯核函数,n取值100,按照式(3)和(4)计算得出高斯核函数的带宽h为1.0595。对图1中的概率密度求其累计分布函数,其结果如图2所示。
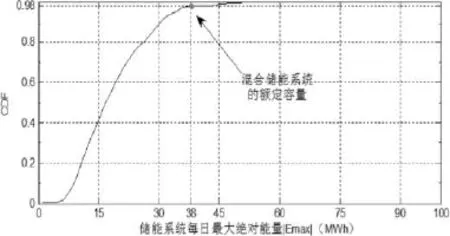
图2||Emax的累积分布函数
图2 为||Emax的累积分布函数,为满足98%储能容量的日需求,图中标出红点所对应的横坐标值即为储能系统的容量,其额定容量为38MWh。
4 结论
本文提出了一种基于核密度估计法的储能系统容量配置的方法。该方法是建立在统计风电功率的预测误差分布的基础之上得出的储能容量配置的方法。它是一种针对某一特定的预测方法,不需要知道分布类型,直接对其统计,可以很好地解决风电功率的预测误差的分布模型受外界扰动因素较多的问题,具有很强的实用性。在此方法统计下得出了混合储能系统的容量和额定功率,实现了储能容量配置的目的。

