Banister模型研究进展及其在训练实践中的应用
Banister模型研究进展及其在训练实践中的应用
田中
(北京市体育科学研究所, 北京100075)
摘要:Banister模型是对训练负荷和成绩关系的数学描述,通过对相关研究文献的梳理,综述了Banister模型的原理、研究进展、局限性、生理学基础及其在训练实践中的应用,旨在促进该模型在我国训练监控中的应用。
关键词:Banister模型;进展;应用
中图分类号:G808.1
收稿日期:2014-11-20
基金项目:北京市体育局科研课题(编号:2014BTP004)。
作者简介:田中(1971-),男,山东费县人,副研究员,博士,研究方向训练监控和高原训练。
Progress of Banister model and its application in training practice
TIAN Zhong
(BeijingInstituteofSportsScience,Beijing100075,China)
Abstract:Banister model is a mathematical model describing the relationship between training load and performance. By summarizing the related researches, the article attempts to review Banister model's underlying mechanism, progress, limitation, physiological base and application in training practice, and to prompt its application in training monitoring.
Key words:Banister model; progress; application
数学模型的运用为解决竞技体育的问题提供了量化工具和理论支撑,美国学者Keller最早把数学模型运用到竞技体育科研领域,他根据运动员的生理学特性,设计出完成特定距离跑步时的最佳跑速[1]。随着现代竞技体育的发展,在训练负荷的控制方面出现了越来越精细化的趋势,训练负荷和成绩的数学建模实现了对训练负荷的精细控制,是训练实践中对训练负荷控制的重要进展。在训练负荷和成绩关系的数学建模方面,Banister以游泳运动员为研究对象,于1975年首次对训练负荷和成绩关系进行了数学描述,并通过对训练负荷和成绩关系的建模研究,建立了较为准确的训练负荷-成绩量化系统[2],即“Banister模型”。之后,出现了大量关于该模型及其改良模型的研究,研究表明“Banister模型”具有良好的建模效果,尽管还存在其他关于训练负荷-成绩关系的模型,“Banister模型”仍是目前研究最多和广为接受的模型。
1Banister模型的原理及演变
1.1Banister模型的原理
解析法和黑箱法是研究机体系统常用的两种方法,解析法是把系统分解为不同的组成部分,然后利用物理和化学原理对每一部分进行描述;与此相反,黑箱法不考虑系统的组成部分,仅考察系统的“输入变量-输出变量”的关系,在这种情况下,输出变量是输入变量通过系统功能转换的结果。基于黑箱法,Banister通过对耐力、力量、技术和心理四个影响运动能力的因素进行分析,并从中抽取训练负荷这一主要因素,对其与成绩的相互关系进行抽象的数学描述,提出了冲量-响应模型(impulse-response,IR),IR模型认为一次急性运动可以刺激机体产生适应,对于提高机体能力具有正向作用,一次急性运动也同样产生短暂的疲劳,对机体能力具有短暂的负面影响,这些急性效应的累积决定了训练成绩[2,3],训练负荷和成绩关系的模型示意图见图1。
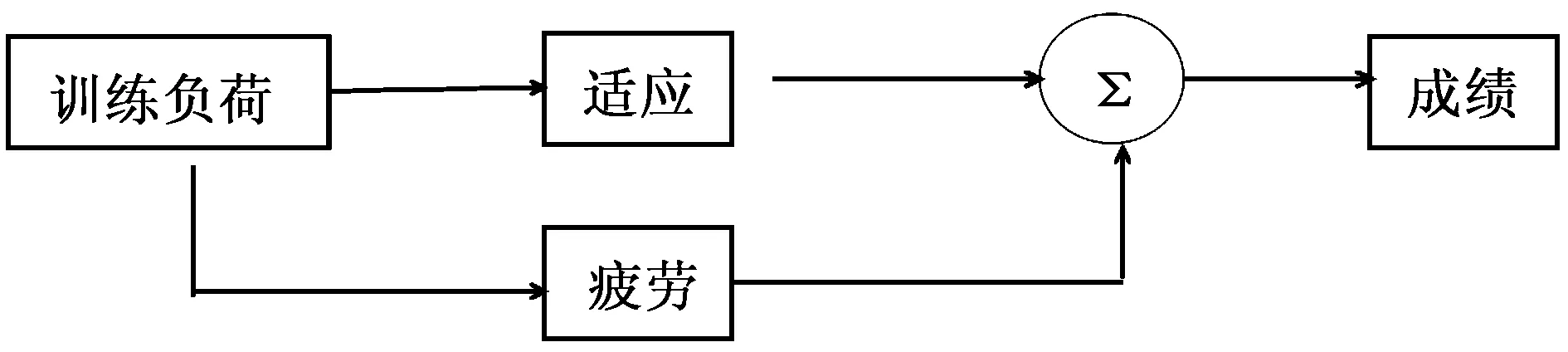
图1 训练负荷和成绩关系模型图
在模型中,输入变量是训练“剂量”(量和强度),输出变量是成绩,成绩是适应和疲劳共同作用的结果,以适应和疲劳两种相互拮抗的函数描述训练负荷的效应,即模型成绩=(适应量)-K*(疲劳量),上述成绩变化的时程可以用一阶微分方程(1)来表达和计算:
(1)
pt代表第t天时的模型成绩,p0代表初始成绩,k1和k2分别为适应和疲劳系数,τ1和τ2代表适应和疲劳时间常数,wi代表第i天的训练负荷量。Banister认为训练后疲劳的积累要大于适应,但适应消退的时间要长于疲劳消退的时间,建议在起始条件下的权重因子k1=1,k2=2,τ1为45天,τ2为15天,这些参数因项目和个体的不同而不同,是设计个体化训练负荷的重要依据[3,4]。利用该公式,可以对适应(正向)和疲劳(负向)效应进行量化,从而检验训练的冲量-响应特性,为设计周期化的训练计划提供参考。
1.2Banister模型的演变
Banister 是最早研究训练负荷和成绩关系的学者,他于1975 年首次尝试用数学建模的方法来量化训练负荷与成绩之间的关系,原始的模型包括技术、心理、耐力和力量四个组成部分,不过该模型很难把影响成绩的技术、心理、耐力和力量四个因素有效的结合在一起分析成绩,也很难准确预测成绩,但该模型为训练负荷和成绩关系的研究奠定了基础,一般称该模型为Banister模型[2,3]。
为弥补Banister模型的不足,Calvert于1976年对该模型进行了改进,排除了缺乏可靠测量手段的心理、力量和技术因素,Calvert在研究中假设训练能够产生两个适应反应(提高成绩)和一个疲劳反应(降低成绩),通过对适应量和疲劳量的数学分析,得到一个简单的一阶微分方程,最终形式是:
p(t)=|(e-t/τ1-e-t/τ2)-Ke-t/τ3|*w(t)
(2)
pt代表第t天时的模型成绩,K代表疲劳幅度系数,τ1和τ2代表适应时间常数,τ3代表疲劳时间常数,wt代表第t天的训练负荷量,该模型默认起始训练负荷为零[3]。Calvert的研究取得了很好的预测效果,尽管有多个模型成绩和实际成绩存在差异,但二者在成绩的变化趋势上是一致的,Calvert认为虽然较为简单的数学模型和训练负荷的量化是造成误差的部分原因,而无法控制的和没有记录的活动是影响成绩误差的主要原因。
然而直到1990年,才由Morton等对模型作了改进[5],他们把Calvert模型中的两个适应因子和一个疲劳因子简化为一个适应因子和一个疲劳因子,分别用下式表达:
适应量:g(t)=g(t-i)e-i/τ1+w(t)
(3)
疲劳量:h(t)=h(t-i)e-i/τ2+w(t)
(4)
适应和疲劳的共同效应以一个简单的线性微分方程来表示,公式为:
p(t)=k1g(t)-k2h(t)
(5)
在Morton改进后的模型中,两名跑步运动员模型成绩和实际成绩的相关系数分别为0.71和0.96,建模效果良好。Busso在Morton研究基础上采用了另一个变形公式来对训练负荷和成绩的关系进行建模研究,Busso的模型更为简单,只有一个适应因素组成模型,数学公式为:
p(t)=w(t)kle-t/τ1
(6)
他们发现估计成绩和实际成绩较为相似,可以解释实际成绩和估计成绩差异的61-87%,认为两元素模型(适应和疲劳)与一元素(适应)模型模拟的情况一样好。但他们也指出模型可能低估了疲劳的作用,其原因可能是训练没有足够的强度,以至于疲劳效果不明显,同时该研究的标准差过大[6]。
Fitz-Clarke等在Calvert的公式基础上应用影响曲线的方法,研究了一个训练周期结束后运动适应与疲劳的变化情况[7],概念性解释了每一个连续的训练日对其后的成绩影响。影响曲线采用的模型和Banister模型相同,但能够更为清晰的描述任何时间的训练对未来某特定时间成绩的影响。此外,Busso也对影响曲线进行了研究,他于1994年对一个链球运动员长达37周的完整训练阶段进行了详细的研究,发现同适应和疲劳模型的计算结果比较,影响曲线的变化和实际成绩更为接近[8]。
Busso等在研究中发现,在一个训练期间,τ和K可能会发生变化,即为时变参数,尤其是当训练强度大时,τ2、K1和K2的变化较大,用线性的固定参数可能不适于描述多样性训练计划的训练应答,需在每次收集数据时都利用以往和目前数据重新计算参数[9]。同固定参数比较,采用时变参数计算获得的结果能更准确反映长期的适应和疲劳,在比较了两种参数估计的方法后,Busso 认为τ1变化对成绩影响不大,而τ2、K1和K2对计算结果影响较大[9]。然而当训练强度不变,训练频度增加时,上述参数无明显变化,但K2增加幅度大于K1增加幅度,预示着过大的训练频度会引起成绩下降[10],在比较了两因素、单因素和递推最小二乘法三个模型后发现K2随着训练负荷的增加而增加[11]。
Mujika等对Banister模型也进行了改良,在研究游泳运动员的赛前减量时,引入了附加项初始成绩P0来计算模型成绩,P0在公式中为固定值(见公式1),也取得了良好的建模效果[12]。此后Gouba等以蹼泳队员为研究对象,也引入了初始成绩P0,但与Mujika不同的是他假设模型成绩都是以前一天的成绩为基础,即采用了动态的P0,而非固定值,结果表明改良模型实际成绩和模型成绩的残差平方和(residual sum of squares,RSS)小于传统Banister模型[13]。
自Banister提出训练负荷-成绩关系的数学模型后,众多学者利用该模型进行了大量研究,其建模研究范围涵盖了跑步、游泳、自行车、举重、链球、蹼泳和体操等众多运动项目,表1总结了其中的代表性研究。

表1 Banister模型的代表性研究
注:k1和k2为适应和疲劳幅度系数,τ1和τ2为适应和疲劳时间常数,r2为模型成绩和实际成绩的相关系数,多名研究对象的结果以平均值±标准差表示。
2Banister模型在训练实践中的应用
2.1在赛前减量训练中的应用
赛前减量训练是训练计划的重要组成部分,是在预期时间里为减低运动员心理上和生理上的压力,以达到最佳竞技状态进行的非线性、渐进式的减少训练负荷的过程,它是一种为了既能够保持训练适应又能够消除训练诱发的疲劳设计的特殊的训练方法,目的是在比赛中保证运动员展现出最好的竞技水平。赛前减量训练包括训练强度、频率等方面的控制,其中何时减量或减量持续的时间是减量训练最难把握的因素。Banister模型在训练实践中的一个重要应用就是赛前减量训练的设计,主要体现为以下三个方面:
第一,训练年限不同时,赛前减量训练的模式不同[3]。Calvert对一名大学游泳运动员长达4年的研究发现,在前2个赛季中,适应和疲劳对成绩的影响程度类似,但在第4个赛季中随着训练年限的增加,运动员适应能力逐渐接近遗传学的最高值,适应能力对成绩的影响逐渐下降,其对成绩的贡献率仅为第一个赛季的1/4,而疲劳对成绩的影响却增加。因此不同训练年限的运动员,其赛前减量训练的模式可能不同,训练年限短的运动员赛前注重训练适应的保持,而训练年限长的运动员偏重于疲劳的消除。
第二,不同类型的运动员,赛前减量的模式不同。不同类型的运动员赛前减量训练的持续时间应不同,Avalos发现同年轻的女子中跑运动员比较,年龄大的男子短跑运动员需要更长的恢复时间[16]。尽管在Banister模型中,适应系数和疲劳系数没有直接的生理学意义,但却为区分不同类型的运动员提供了参考,Morton认为拥有较大疲劳系数的个体,成绩受疲劳的影响大,为疲劳主导型;同样,拥有较大适应系数的个体,成绩受适应的影响大,为适应主导型。在赛前减量训练阶段,疲劳主导型运动员需要更长的时间才能恢复,而适应主导型个体恢复速度相对会更快[5]。
第三,赛前减量训练的量化设计。教练员一般根据经验设计赛前减量的时间,往往带有很大的主观性和不确定性,Banister模型的运用为准确把握赛前减量训练提供了量化工具,Fitz-Clarke根据Banister模型利用影响曲线研究赛前减量训练[7],根据影响曲线的概念赛前减量训练是影响曲线的纵坐标值开始为负值的时间点,此时间点后的训练更多地是引起疲劳效应而非适应效应,计算公式为:
τ1和τ2分别为适应和疲劳时间常数,k1和k2分别为适应和疲劳系数,从公式可以看出赛前减量训练的时间是由四个个体化的模型参数决定的。利用影响曲线可以识别达到最好状态所需的时间,这为赛前减量训练提供了参考,Fitz-Clarke认为最佳减量期为赛前的15.8±6.5天,其他学者通过参数估计得出各种赛前减量训练的时间应为2~4周[17],Banister通过对三项全能运动员的赛前减量建模研究,认为指数减量比线性减量更为有效[18]。在Morton利用Banister模型对跑步运动员的赛前减量训练研究中,完全停止训练会带来更好的效果,但在实践中几乎没有运动员使用这种极端的减量模式,与实践不符的原因可能和负荷计算及影响成绩的无法控制的和未记录的因素[5]有关。影响曲线为设计最佳训练计划提供了理论模型,作为研究赛前减量训练的新方法,该方法尽管有较多的研究支持,但还需要实际的实验干预来确定其准确与否[19]。
2.2赛前最佳训练期的量化设计
在赛前减量训练前,为获得成绩更大幅度的提高,通常安排2~4周的超负荷训练,该阶段对成绩的贡献最大,称为最佳训练期,同赛前减量训练不同,该阶段往往保持较高的训练负荷,而训练负荷的增加容易导致运动员生理和心理方面的失调,因此该阶段成绩又往往表现为下降。根据Fitz-Clarke影响曲线的概念[7],赛前最佳训练期是影响曲线在纵坐标上达到最高值的时间,计算公式为:
τ1和τ2分别为适应和疲劳时间常数,k1和k2分别为适应和疲劳系数。同减量训练一样,赛前最佳训练期也是由四个个体化的模型参数决定的。虽然计算所得的tg为某个训练日,但最佳训练期可以围绕tg向前、后扩展为一时间区段,从而形成一个在影响曲线上以tg为中心的高值平台时段,但向后(比赛日方向)扩展的最大期限不应超过影响曲线纵坐标为0的点(即赛前减量的第一天)。影响曲线上对成绩贡献最大的阶段一般为赛前的12至4周,其中第6周为最高值,该阶段的训练负荷宜大,而向左外推影响曲线发现距离比赛5个月之前的训练对成绩几乎没有影响[20]。多项利用Banister模型的研究表明在减量训练前,提高训练量和/或强度能够更大幅度的提高成绩,但减量训练期相对需要更长,如Thomas使用Banister模型发现游泳运动员在赛前减量开始前安排为期28天的超负荷期(负荷提高20%)能够更大幅度的提高成绩[21,22],这与Hellard等的研究是类似的[23]。
2.3模拟训练设计
科学的训练计划对于运动员在比赛中取得好成绩具有重要的意义,训练计划包含质和量两个方面,即需要采取哪种训练和练多少?训练的质是指训练周期的设计,在训练周期的设计方面,Bompa等学者进行了详细的探讨[24],但关于训练的量方面的研究却较少。Banister模型的出现为赛季训练负荷量分布及其对成绩影响的研究提供了理论工具, Banister模型模拟训练的基本原理是利用前述的方法求得模型参数,建立数学模型,再利用该模型预测假定的输入变量(训练负荷量)的输出变量(成绩),从而计算要达到期望的成绩所需的训练负荷量[25]。利用该模型进行模拟训练负荷设计,主要的目的是既能够在比赛日期最大化成绩,又能够尽可能避免过度训练。尽管在训练实践中,最大化成绩和预防过度训练在属性上是拮抗的,但由于这些因素是相互影响的,因此存在同时达到这两个目的的可能性[20]。Morton最早基于Banister模型进行了模拟训练,通过分析影响最大化成绩和过度训练的主要因素后发现:三角形的训练负荷分布结构、隔日高强度训练和短周期(150天)比其他训练模式更能够最大化成绩并减少过度训练发生的风险[17]。同样,Thomas借助影响曲线的概念,以非运动员和优秀游泳运动员为研究对象,利用计算机模拟训练发现在减量训练的最后3天训练负荷增加20~30%能够取得更好的成绩,并且不影响疲劳的消除[26]。
2.4过度训练的预防
过度训练的发生不仅导致成绩下降,同时对运动员的健康也带来了不良影响,运动员在最大化成绩的过程中,需尽量避免过度训练的发生,因此如何诊断和预防过度训练对于运动员具有重要的意义。除使用激素、血清酶等常用指标诊断和预防过度训练外,Banister模型在预防过度训练方面也具有一定的参考价值。Morton以Banister提出的TRIMP来计算疲劳量,认为在可承受的训练和过度训练之间存在一个阈值,该阈值为1000训练单位的疲劳量,并以过度训练应激指数(index of overtraining stress)来评估发生过度训练的风险,过度训练应激指数是指超过该阈值的所有训练日的超阈值疲劳量的总和与日均超阈值疲劳量的乘积。根据过度训练应激指数概念,当超过阈值后,疲劳累积量相同时,日均超阈值量大的队员易出现过度训练,而相同日均超阈值量时,训练周期更长的队员过度训练的风险更高。过度训练量的阈值一般确定为1000训练单位,但该值并非是不变的,对于年轻和高水平的运动员来讲阈值会更高,日均负荷量125训练单位的队员疲劳阈值可以达到1500训练单位[17]。虽然Lucia等通过对自行运动员的研究提出了其安全的Trimp阈值以预防过度训练[27,28,29],但在使用Banister模型预防过度训练方面,之后并没有出现研究,还需要更多的证据来支持。
3Banister模型的生理学基础和局限性分析
3.1Banister模型的生理基础
尽管Banister模型关于适应、疲劳和成绩的建模概念存在某种程度的主观性,但研究表明模型关于疲劳和适应的计算结果与一些生化指标的变化存在一定的一致性,这为利用Banister模型进行训练监控提供了生理学证据。
Banister在铁代谢、血清酶的变化与模型适应量、疲劳量方面进行了研究,首先于1985年对5名女子长跑运动员进行了为期300天的研究,测量了红细胞总数、血红蛋白、血清铁、铁蛋白、总铁结合力和转铁蛋白饱和度等血液指标,以TRIMP计算训练负荷量,按照模型计算疲劳量和适应量,该研究发现当疲劳量增加时,转铁蛋白饱和度也增加,而直到减量时转铁蛋白饱和度才下降,反映了疲劳量增加时铁的吸收和运输能力下降,易导致贫血的发生,而疲劳量下降时伴随铁吸收的增加,血红蛋白浓度也升高[30]。在血清酶方面,Banister通过测量血清CK、LDH和AST等的变化和计算模型适应量、疲劳量,发现其变化模式同铁代谢类似,但在时程上稍延迟于适应量和疲劳量的变化[31,32]。其后Busso研究了举重运动员血清激素与疲劳量、适应量的相关性,发现促黄体素和睾酮的变化与适应量显著相关,相关系数达到0.90和0.73[33,34]。Wood的研究为Banister模型的生理基础提供了最有力的证据,该研究的主要目的是确定公式适应、疲劳系数与生理学指标的关系,研究发现通气无氧阈跑速、跑步经济性和模型适应系数的相关系数分别为0.94和0.61,而反映疲劳的POMS分值和疲劳系数的相关系数为0.75[35]。
3.2Banister模型的局限性分析
目前Banister模型多限于实验性研究,尽管模型能够模拟人体疲劳、适应和成绩的一般变化,但一些因素限制了在实践中的应用,主要有以下几个方面[14,36]:
首先是预测未来成绩的精确性尚受到怀疑,这也限制了模型在最佳化训练负荷规划中的利用。其次,是估计成绩和实际成绩之间的差异,Busso的改良模型能够更好拟合实际成绩,但却增加了数学上的复杂性和难度,并需要更多的数据。而且模型假设没有成绩的上限,增加训练负荷就能够产生更好的成绩,但在实践中存在即使增加负荷量也无法进一步提高成绩的平台。生理学机制方面的证据不够充分也是其局限性之一,尽管模型能够准确描述成绩的动态变化,且时间常数具有一定的生理学意义,但模型和训练诱导的疲劳、适应的特异性生理适应如肌糖原的再合成、线粒体的再生等的关联性还缺乏令人信服的证据。另外,需要记录大量的训练数据和频繁的成绩测试也限制了模型的广泛应用。
4研究展望
自Banister提出训练负荷与成绩关系的数学模型后,众多学者在模型的处理过程方面进行了大量改进工作,生物能学(bioenergetics)等新的训练负荷量化方法[37]以及多种便携式实时训练监控设备的不断出现,对模型的输入即训练负荷的量化将更为精确,但找出能够表达运动员承受真实负荷的计算方法,尤其是如何计算大强度、极量强度训练所产生的应激以及如何计算不同项目运动员承受的真实负荷还有待于研究[38];另外,基于“Banister模型”专项性的模拟训练负荷设计系统,将进一步推动该模型越来越多地应用于训练实践和提升制定个体化训练计划的科学性。国外关于训练负荷与成绩数学模型的研究已经较为成熟,而国内仅有何勇等在该领域开展了研究[39], 尽管“Banister” 模型存在局限性,但开展该模型的研究无疑是是对训练监控理论和手段的重要补充。
参考文献:
[1]Keller J B. A theory of competitive running [J]. Physics Today,1973,26(9):43-47.
[2]Banister E W, Calvert T W, Savage M V,etal. A systems model of training for athletic performance [J]. Aust J Sports Med, 1975,7(5):57-61.
[3]Calvert T W, Banister E W, Savage M V,etal.A systems model of the effects of training on physical performance [J].IEEE Transactions Systems, Man and Cybernetics,1976, 6(2): 94-102.
[4]Taha T, Thomas SG. Systems modelling of the relationship between training and performance[J].Sports Med,2003,33(14):1061-1073.
[5]Morton RH, Fitz-clarke JR, Banister EW. Modeling human performance in running[J]. J Appl Physiol,1990,69(3):1171-1177.
[6]Busso T, Carasso C, Lacour J R. Adequacy of a systems structure in the modeling of training effects on performance[J]. J Appl Physiol, 1991, 71(5): 2044-2049.
[7]Fitz-clarke J R, Morton R H, Banister E W. Optimizing athletic performance by influence curves[J]. J Appl Physiol, 1991, 71(3): 1151-1158.
[8]Busso T, Candau R, Lacour J R. Fatigue and fitness modelled from the effects of training on performance[J]. European Journal of Applied Physiology and Occupational Physiology, 1994, 69(1): 50-54.
[9]Busso T, Denis C, Bonnefoy R,etal.Modeling of adaptations to physical training by using a recursive least squares algorithm[J]. Journal of Applied Physiology, 1997, 82(5): 1685-1693.
[10]Busso T, Benoit H, Bonnefoy R,etal.Effects of training frequency on the dynamics of performance response to a single training bout[J]. J Appl Physiol,2002, 92 (2): 572-580.
[11]Busso, T. Variable dose-response relationship between exercise training and performance[J]. Medicine & Science in Sports & Exercise, 2003,35(7), 1188-1195.
[12]Mujika I,Busso T,Lacoste L.Modeled responses to training and taper in competitive swimmers[J]. Medicine & Science in Sports & Exercise,1996,28(2):251-258.
[13]Gouba E, Konfe B O, Nakoulima O,etal.Applying a Mathematical Model to the Performance of a Female Monofin Swimmer[J]. Applied Mathematics, 2013, 4(12): 1673-1681.
[14]Hellard P, Avalos M, Lacoste L, Barale F, Chatard JC, Millet GP.Assessing the limitations of the Banister model in monitoring training[J]. J.Sports Sci,2006, 24(5): 509-520.
[15]Sanchez AM, Galbès O, Fabre-Guery F.etal.Modelling training response in elite female gymnasts and optimal strategies of overload training and taper[J], J.Sports Sci, 2013, 31(14): 1510-1519.
[16]Avalos M, Hellard P, Chatard J C. Modeling the training-performance relationship using a mixed model in elite swimmers[J]. Medicine & Science in Sports & Exercise,2003, 35(5): 838-846.
[17]Morton R. H. The quantitative periodization of athletic training:model study[J].Sports Medicine, Training and Rehabilitation: An International Journal, 1991,3(1),19-28.
[18]Banister, E. W., Carter, J. B.,Zarkadas, P. C.Training theory and taper: Validation in triathlon athletes l[J]. Eur J Appl Physiol Occup Physiol,1999,79(2),182 -191.
[19]Pyne D B, Mujika I, Reilly T. Peaking for optimal performance: Research limitations and future directions [J].J.Sports Sci, 2009, 27(3): 195-202.
[20]Morton R. H. Modelling training and overtraining [J]. J.Sports Sci, 1997, 15(3):335-340.
[21]Thomas L., Mujika I,Busso T. A model study of optimal training reduction during pre-event taper in elite swimmers [J]. J.Sports Sci,,2008, 26(6), 643-652.
[22]Thomas L. and Busso T. A theoretical study of taper characteristics to optimize performance[J].Medicine and Sciences in Sports and Exercise, 2005,37(9): 1615-1621.
[23]Hellard P, Avalos M, Hausswirth C,etal.Identifying Optimal Overload and Taper in Elite Swimmers over Time[J]. Journal of sports science & medicine, 2013, 12(4): 668-678.
[24]Bompa T O. Periodisation as a key element of planning[J]. Sports Coach, 1987, 11(1): 20-23.
[25]Thierry Busso,Luc Thomas. Using Mathematical Modeling in Training Planning[J]. Int J Sports Physiol Perform,2006,1(4):400-405.
[26]Thomas L, Mujika i, Busso T. Computer simulations assessing the potential performance benefit of a final increase in training during pre-event taper[J]. J Strength Cond Res, 2009, 23(6): 1729-1736.
[27]Lucia A, Hoyos J, Santalla A,etal.Tour de France versus Vuelta a Espa?a: which is harder[J].Med Sci & Sports Exerc,2003,35(5):872-878.
[28]Luciá A, Hoyos J, Carvajal A,etal.Heart rate response to professional road cycling: the Tour de France[J]. Int J Sports Med,1999,20(3):167-172.
[29]Lucía A, Hoyos J, Chicharro JL. Preferred pedalling cadence in professional cycling[J].Med Sci Sports Exerc,2001,33(8):1361-1366.
[30]Banister E. W. Hamilton C. L..Variations in iron status with fatigue modelled from training in female distance runners[J].Eur J Appl physiol,1985,54(1):16-23.
[31]Banister EW, Fitz-Clarke JR. Plasticity of response to equal quantities of endurance training separated by non-training in humans [J]. J Thermal Biol,1993, 18(5-6): 587-597.
[32]Banister EW, Morton RH, Fitz-Clarke J. Dose/response effects of exercise modeled from training: physical and biochemical measures[J]. Ann Physiol Anthropol,1992,11(3): 345-356.
[33]Busso T, Hakkinen K, Pakarinen A, Carasso C, Lacour JR, Komi PV, Kauhanen H. A systems model of training responses and its relationship to hormonal responses in elite weight-lifters[J]. Eur J ApplPhysiol Occup Physiol,1990,61(1-2): 48-54.
[34]Busso T, Hakkinen K, Pakarinen A, Kauhanen H, Komi PV, Lacour JR. Hormonal adaptations and modelled responses in elite weightlifters during 6 weeks of training[J]. Eur J Appl Physiol Occup Physiol,1992,64(4):381-386.
[35]Wood RE, Hayter S, Rowbottom D, Stewart I. Applying a mathematical model to training adaptation in a distance runner[J]. Eur J Appl Physiol, 2005,94(3): 310-316.
[36]Clarke DC, Skiba PF. Rationale and resources for teaching the mathematical modeling of athletic training and performance[J]. Adv Physiol Educ,2013,37(2): 134-152.
[37]Hayes PR1, Quinn MD.A mathematical model for quantifying training[J]. Eur J Appl Physiol,2009,106(6):839-847.
[38]朱那,盛蕾,曹佩江.Trimp 在竞技体育训练监控中的应用[J].体育与科学,2011,32(2):81-87.
[39]何勇,虞丽娟,吴卫兵.训练负荷—体能状态关系的数学建模[J].上海体育学院学报, 2011,35(2):57-60.

