时标上的二阶变时滞中立型动力方程的振动性

林文贤

（韩山师范学院数学与统计学院，广东潮州 521041）

时标上的二阶变时滞中立型动力方程的振动性

林文贤

（韩山师范学院数学与统计学院，广东潮州 521041）

利用广义Riccati变换和完全平方技巧，研究了一类时标上的二阶变时滞中立型动力方程的振动性质，获得了这类方程在一定条件下所有解振动的若干振动准则，其结果不仅推广和包含了已知的一些结果，而且在时标上统一了二阶中立型微分方程和差分方程解的振动性质.

时标；动力方程；振动性；广义Riccati变换

1 引言

为了统一微分和差分，1988年德国学者Stefan Hilger在他的博士论文[1,2]中首次提出了测度链微积分（The calculus of measure chains）.他的博士导师Bernd Aulbach教授指出，这种新的微积分有三个主要目的：统一、推广和离散化（Unification-Extension-Discretization）.而对于许多情况，我们只需考虑测度链（measure chains）的一种情形——时标（Time Scale）.一个时标指的是实数集ℝ的任一非空闭子集，它具有由ℝ诱导的拓扑以及ℝ中的顺序关系，通常用记号T表示.对于定义在T上的函数y，我们考虑其上的所谓Δ-导数yΔ和n阶时标动力方程（Dynamic Equations on Time Scale）f(t,y,yΔ,yΔΔ,…,yΔn)=0.当T=ℝ为实数集时，这种导数yΔ是通常的导数y′，这些动力方程即是微分方程；而当T=ℤ为整数集时，这种导数yΔ是通常的前差分Δy（the forward difference），这些动力方程则是差分方程.特别重要的是，除了T=ℝT=ℤ外，还有许多十分有趣的其它形式的时标，如T=qℤ:={qk|k∈ℤ}⋃{0}，其中q＞1；T=hℤ:={hk|k∈ℤ}，其中h＞0；，其中a,b＞0；T={tk|k∈ℤ}，其中对所有k∈ℤ有tk∈R且tk＜tk+1.

这些时标给我们提供广泛的应用空间.需要强调的是：尽管微分方程和差分方程有许多类似的结果，但仍然存在大量本质上完全不同的性质和结论.

对时标理论（The theory of time scale）的研究，既是数学理论自身发展的需要，也是实际问题的需要.时标理论的研究不仅能把微分方程理论和差分方程理论很好地结合在一起，而且所有结果比微分方程和差分方程理论的更为广泛，它能够把这些古典情形扩充到“两者之间”，例如扩充到所谓的q-差分方程（在量子理论方面有重要的应用）.由于实际模型所对应的时标动力方程可解决把停止一一开始行为和连续行为结合在一起的问题，因此计算机网络、生态、工程技术、物理等领域的许多现象用时标动力方程来描述，更能揭示其本质属性.譬如，利用这一理论建立的昆虫种群模型和电网模型更符合实际[3-4].

文献[5]中称“这种时标动力方程是更能反映现实世界的方程式”.

近十几年来，对时标上动力方程的振动性和非振动性理论的研究已经得到国内外许多学者的极大关注，发展迅速，取得了大量的成果[6-28].

本文将考虑如下的一类二阶非线性变时滞中立型时标动力方程

其中自变量t在时标T上变化.这里supT=∞且h(t)→∞(t→∞).

在T上本文定义了前跳算子σ(t):=inf{s∈T:s＞t}和后跳算子ρ(t):=inf{s∈T:s＜t}.对于函数f:T→ℝ，我们说fΔ(t)是f在t∈T处的Δ-微分，如果

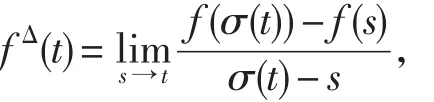
存在（此处fΔ(t)要求t∈Tk:=T{m}，如果m存在，其中m是指T的最大孤立点），并且对任意的ε＞0，存在U=(t-δ,t+δ)⋂T使得

对所有t∈T成立.f的Δ-微分与其步差算子μ(t)≐σ(t)-t之间存在着重要关系fσ=f+μfΔ，其中fσ=f∘σ.对任意的两个Δ-微分的函数f和g，其乘积与商的Δ-微分分别为

不妨设Crd(T,S)是表示T上的所有右稠连续函数f:T→S⊆ℝ的一个集合.称f在t∈T上是右稠连续的，如果f在所有右稠密点连续（所谓右稠密点是指满足σ(t)=t的点）且在所有的左稠密点（ρ(t)=t）和右发散点（σ(t)＞t）的左极限存在.文献[3]表明右稠密点连续函数一定有原函数.其Cauchy积分由定义，其中t∈T.如果a∈T,supT=∞且f是[a,∞)上的右稠连续函数，则可定义广义积分如下，如果极限存在，称广义积分是收敛的，如果极限不存在，则称广义积分是发散的.当a,b∈T,f,g∈Crd时，有[3]

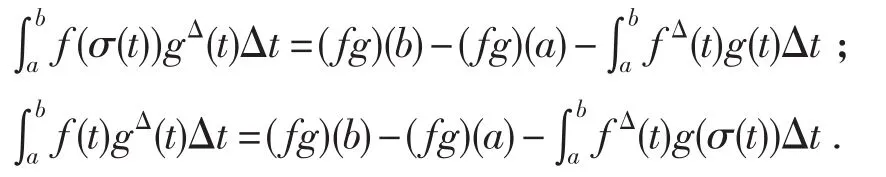
方程（1）的一个解是指定义在T的区间[b,∞)上的一个实值函数x，且在[c,∞)上满足（1），其中c＞b足够大使得h(t)≥b,t≥c，称（1）的一个解x:T→ℝ是（1）的一个最终正解，若存在t0∈T使得x在[t0,∞)是正的.考虑到时标或许是不连续的，我们说函数x:T→ℝ在h∈T有一个一般的零点，如果x(h)=0或者h左发散的（ρ(h)＜h）且x(h)x(ρ(h))＜0.我们说方程（1）的一个解是振动的，如果对任何r∈T存在一个t∈T满足t＞r使得x在t有一个一般的零点.

本文的目的是利用广义Riccati变换、完全平方技巧和参数函数而得到时标动力方程（1）的新的振动准则，推广和包含了文献[17-19]的结果，并且在时标上统一了二阶中立型微分方程和差分方程解的振动性质.

2 主要结果

[1]HILGERS.EinMabkettenkalkulMitAnwendungaufZentrumsmannigfaltigkeiten[D].Wurzburg：UniversityWurzburg,1988.

[2]HILGER S.Analysis on measure chains-a unified approach to continous and discrete calculus[J].Results Math,1990,18（1）:18-56.

[3]MARYTIN B,ALLEN P.Dynamic Equations on Time Scales:An Introduction and Applications[M].Birkhäuser,Boston,2001.

[4]AGARWAL R,BOHNER M.O’regan D,Peterson A.Dynamic equations on time scales:a survey[J].J Comput Appl Math, 2002,141（1/2）:1-26.

[5]瓦妮萨-斯佩丁.征服自然界的数字[N].参考消息，2003-08-13[7].

[6]KAYMAKCALAN B,LAKSHMIKANTHAN V,SIVASUNDRAM S.Dynamic Systems on Measure Chains,Mathematics and its Applications[M].Dordrecht：Kluwer Academic Publishers,1996：370.

[7]AGRWAL R,BOHNER M.Basic calculus on time scales and some of its applications[J].Results Math,1999,35:3-22.

[8]ERBE L,MATHSEN R,PETERSON A.Factorng linear differential operators on measure chains[J].Journal of Inequalities and Applications,2001,6（2）:287-303.

[9]LIN Wenxian.A note on oscillation for systems of high order quasilinear partial differential eqations of neutral type[J].Applied Mathematics and Computation,2004,156（3）:563-576.

[10]林文贤.一类非线性偶数阶中立型方程的振动准则[J].工程数学学报，2005，22（1）：159-162.

[11]林文贤.一类具连续偏差变元的二阶非线性中立型方程的振动性[J].西南师范大学学报:自然科学版，2009，34（4）：1-3.

[12]LIN Wenxian.Interval oscillation theorems for certain second order neutral differential equations with continuous deviating arguments[J].Southeast Asian Bulletin of Mathematics,2010，34（6）:1055-1061.

[13]林文贤.具有阻尼项的中立型Emden-Fowler方程的区间振动准则[J].韩山师范学院学报，2011，32（6）：8-11.

[14]LIN Wenxian.A note on oscillation of certain second order partial functional differential equation with damping[J].Pioneer Journal of Mathematics and Mathematics Sciences,2012，4（1）:125-128.

[15]林文贤.具连续分布时滞的二阶半线性中立型阻尼泛函微分方程的Philos型振动定理[J].韩山师范学院学报，2012，33（3）：7-12.

[16]林文贤.具连续偏差变元的二阶阻尼微分方程的振动性[J].中国科学院研究生院学报，2012，29（5）：594-598.

[17]吴洪武，谢胜利，徐远通.时标上的二阶变时滞动力方程的振动准则[J].数学的实践与认识，2007，37（20）：131-135.

[18]王艳群，罗李平.时标上的二阶变时滞动力系统的振动准则[J].衡阳师范学院学报，2010，31（3）：18-21.

[19]林文贤.时标上的二阶变时滞中立型动力方程的振动性[J].韩山师范学院学报，2012，33（6）：6-10.

[20]林文贤.一类具阻尼项和连续分布滞量的偶数阶中立型方程的振动性[J].西南师范大学学报:自然科学版，2012，37（9）：1-3.

[21]LIN Wenxian.Oscillation theorems for certain higher order neutral equations with continuous distributed deviating arguments[J].Southeast Asian Bulletin of Mathematics,2012，34（4）:849-854.

[22]林文贤.一类中立型阻尼泛函微分方程的振动性[J].四川师范大学学报：自然科学版，2013，36（3）：20-22.

[23]林文贤.一类三阶中立型阻尼方程的Philos型振动定理[J].宁夏大学学报：自然科学版，2014，35（2）：1-4.

[24]林文贤.一类带强迫项的二阶阻尼微分方程的区间振动性[J].郑州大学学报：理科版，2014，46（2）：1-5.

[25]林文贤，俞元洪.高阶中立型时滞微分方程的振动准则[J].应用数学学报，2014，37（6）：1018-1024.

[26]林文贤.振动性和周期解理论的研究[M].北京：国防工业出版社，2014.

[27]林文贤.具分布式偏差变元和阻尼项的中立型双曲方程的振动性[J].西南师范大学学报：自然科学版，2015，39（1）：1-4.

[28]林文贤，郑伟珊.一类具阻尼项的二阶半线性泛函微分方程的振动性[J].井冈山大学学报：自然科学版，2015，36（3）：21-24.

Oscillation for Second-Order Neutral Dynamic Equations with Variable Delay on Time Scales

LIN Wen-xian
（School of Mathematics and Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041）

By using the generalized Riccati transformation and the averaging technique,the oscillation for a class of nonlinear second-order neutral dynamic equations with variable delay on time scales is discussed and some new oscillation criteria are obtained.The results extend and include some known results,but also unify the oscillation of the second-order neutral differential equations and the second-order neutral difference equations.

time scale；dynamic equation；oscillation；generalized Riccati transformation

O175.12；O175.14

A

1007-6883（2015）06-0008-06

责任编辑 朱本华

2015-09-11

广东省高等教育教学改革项目（项目编号：GDJG20142396）；广东省高等学校特色创新项目（项目编号：2014GXJK125）.

林文贤（1966-），男，广东潮州人，韩山师范学院数学与统计学院教授.