一种估计锂电池充电状态的分数阶阻抗模型
杨晴霞,曹秉刚,徐俊,李秀青,宁博,王斌
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学材料科学与工程学院,710049,西安)
一种估计锂电池充电状态的分数阶阻抗模型
杨晴霞1,曹秉刚1,徐俊1,李秀青2,宁博1,王斌1
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学材料科学与工程学院,710049,西安)
针对电动汽车动力锂电池的充电状态估计问题,提出一种基于锂电池电化学阻抗谱的分数阶阻抗模型。该模型通过对不同频率下的锂电池电化学阻抗谱进行分析,归一化为一种简单的等效电路,引入分数阶建模思想,设计与分数阶阻抗模型相适应的分数阶卡尔曼滤波器,利用锂电池HPPC测试对该模型进行参数辨识,使用Simulink软件对锂电池的工作电压以及充电状态进行仿真,并将仿真结果与测试结果进行对比分析。分析结果表明:利用所建立的分数阶阻抗模型对锂电池工作电压进行估计,其误差可以稳定在0.05 V以内;对初始状态未知的锂电池的充电状态进行估计,其误差可以有效地稳定在2%以内。所建立的分数阶阻抗模型可以准确地预测锂电池的充电状态,可为电动汽车动力电池管理系统提供有效的状态估计。
锂电池充电状态;分数阶阻抗模型;分数阶卡尔曼滤波器
随着能源危机以及气候变暖等全球问题的发展,人们更加重视节能减排并且提倡低碳经济。电动汽车的动力由电池系统来提供。电动汽车以路面零排放及低能耗的特点越来越受到社会各界的认可和重视[1]。电动汽车大规模生产受到关键技术的制约,这些关键技术包括:驱动电机、动力电池及电池管理系统、电机控制及能量回收系统等[2]。
动力电池以及电池管理系统是制约电动汽车发展的主要技术瓶颈之一,电动汽车可采用锂电池作为电动汽车的动力来源。在不同使用环境下,锂电池的性能会发生改变,需要对电池的状态进行实时监控。通常电池的状态包括电池的充电状态(SOC)、电池的健康状态(SOH)以及电池的性能状态(SOF),由电池容量的衰退来决定[3-4]。
Alvin等提出了Li/SO2基于模糊逻辑的充电状态估计算法,该算法的精度只能保证在10%左右[5]。Kozlowski提出了自回归平滑的方法来估算不同电池的充电状态,基于电池内部电解液内阻、电荷转移内阻以及双极电容变化等电池内部特征作为二阶自回归平滑模型的输入[6],但这些参数在非实验室条件下很难获得。Hansen等提出基于支持向量机的充电状态经验模型,其分析结果表明基于支持向量机充电状态与理想的充电状态误差范围为-10%~15%[7],误差较大,结果并不是非常理想。Blanke等提出了基于阻抗谱数据的充电状态预测方法,但该方法需要大量电化学阻抗谱数据来进行分析,很难在实验室外实现[8]。葡萄牙波尔图大学学者Machado研究表明,即使系统的所有个体具有整数阶动态,但是系统的整体动力学特性也可能是分数阶的[9]。
电池是强非线性电化学系统,电池模型主要可分为两大类,即电化学模型和等效电路模型[10]。电化学模型从电化学动力学的角度对电池进行建模,需要全面考虑电池工作时内部的电化学反应,需要复杂的电化学理论等知识,其模型普遍较为复杂[11];等效电路模型利用电压源、电阻、电容等电气元件的组合来表征电池的特性,包括Rint模型、RC模型、一阶RC模型、二阶RC模型等[12]。
本文首先提出基于锂电池电化学阻抗谱以及充电脉冲响应的锂电池等效电路,然后基于该等效电路提出分数阶阻抗模型,通过进行实验并利用最小二乘法对该阻抗模型进行参数辨识,最后利用分数阶卡尔曼滤波器对锂电池UDDS(urban dynamometer driving schedule)工况下的工作电压以及充电状态进行估计。
1 基于阻抗谱的锂电池阻抗模型
1.1 锂离子电池的电化学阻抗谱及其等效电路
锂离子电池的电化学阻抗谱是指将一系列不同频率振幅的正弦波信号施加在锂离子电池上所得到的相应频域内的电信号反馈。电化学阻抗谱分析不仅可以获得电池快速响应过程,还能获得其长时间响应过程,被认为是描述电池特性的最佳方法之一[13]。锂离子电池的电化学阻抗谱随着锂电池的充电状态会发生改变[13-15],如图1所示。

图1 不同充电状态下锂电池的阻抗谱
在图1所示的阻抗谱中,在不同的充电状态下,锂电池的阻抗谱并不一致,但其基本形状保持了高度的一致性。在阻抗谱中,高频段与实轴相交的部分表征锂电池的欧姆电阻,又称为欧姆极化;在中频部分显示为压扁的半圆,表征了锂电池内部固体电解质界面(solid electrolyte interface, SEI)膜上电荷转移情况,即锂电池内部的活化极化,可用常相元件以及电阻的并联来表示;在其低频部分显示为压扁半圆的一部分,表征频率较低时锂电池内部离子的扩散行为,又称为锂电池的浓差极化。
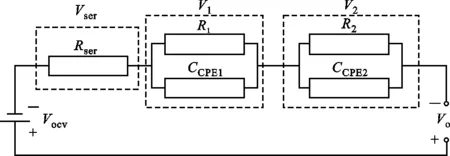
图2 基于电化学阻抗谱的锂离子电池等效电路
经过以上分析,可将不同的阻抗谱归一化为一种比较简单的等效电路,如图2所示。其中Rser表示锂电池的欧姆电阻,
对应阻抗谱中的高频段,Vser
表征Rser在锂电池内部的分压;R1以及常相元件CCPE1并联表示锂电池的活化极化现象,对应阻抗谱中的中频段,V1表示R1与CCPE1并联处的分压;R2以及常相元件CCPE2并联表示锂电池的浓差极化现象,对应阻抗谱中的低频段,V2表示R2与CCPE2并联处的分压。
1.2 分数阶等效电路模型
分数阶微积分是研究任意实数阶微积分的应用数学,是古典整数阶微积分的自然延伸[16],研究表明,分数阶微积分建立的系统模型更加精确[17]。常见的分数阶微积分的定义包括Caputo分数阶微分定义、Riemaim-Liouville(R-L)分数阶微积分定义以及Griimvald-Letnikov(G-L)分数阶微积分定义3种[15],其中G-L分数阶微积分定义为
(1)

r∈R,为任意实数。
图2中两个常相元件可以用分数阶单元分别描述[18]为
(2)
式中:α∈R,0≤α≤1;β∈R,0≤β≤1。当α=1或者β=1时,CCPE1,CCPE2分别是电容值为C1、C2的电容。
根据电路理论以及图2可以得到如式(3)、(4)所示的电路关系。
(3)
(4)
式中:I为电路电流,放电为正,充电为负。
根据锂电池的充电状态与开环电压的关系(z-Vocv),采用增益调度法[18]对其进行描述
(5)
式中:z表示锂电池的充电状态;Δz表示z的区间段;(ki,bi)表示在第i个z区间段内的参数。
将z-Vocv关系引入由电化学阻抗谱得到的分数阶模型当中,锂电池的分数阶模型为
(6)
(7)
式中:Cn表示锂电池的容量。
对以上电路关系进行整理,可得到分数阶阻抗模型的状态空间模型
(8)
式中:

2 基于分数阶卡尔曼滤波器的充电状态估计
在模型特性未知的情况下,可用卡尔曼滤波器对模型进行估计。Plett在其论文中系统地解释了卡尔曼滤波算法在锂电池的充电状态估计上的应用,提出卡尔曼滤波算法是一种基于精确模型的算法[19-21]。卡尔曼滤波器将电池的当前状态与过去状态进行比较,引入计算值与测量值的误差反馈,通过模型参数的调整,实现精准预测。
前文提出一种锂电池分数阶阻抗模型,其中定相元件通过分数阶进行描述,使用传统的卡尔曼滤波器很难实现,因此提出分数阶卡尔曼滤波器。
针对上文提出的模型,将其根据随机理论进行离散化
(9)
式中:Ik为系统在k时刻的输入;yk为系统的输出;xk为系统的状态向量;ωk、vk分别为系统的测量高斯白噪声和输出高斯白噪声,假设两者相互独立。
在文献[15]中,基于G-L定义的分数阶微分可以描述为
(10)
式中:TS为系统的采样时间,本文采用0.1 s;

系统的离散方程可表述为
(11)

3 仿真实验及分析
3.1 参数辨识
电化学阻抗谱需要在实验室条件下得到,实时在线条件下很难实现,为了进行参数辨识,本文在室温条件下对某锂电池进行混合动力脉冲特性(hybridpulsepowercharacteristic,HPPC)测试(充电状态每下降10%进行一次脉冲测试,采用9.8A充电电流以及14.5A放电电流),HPPC测试电压、电流响应分别如图3所示。

(a)电压响应

(b)电流响应图3 某锂电池的HPPC响应
图4是在充电状态为60%时对某锂电池进行脉冲测试时的电压响应,主要可以分为3部分,其中欧姆电阻Rser造成电压的快速下降以及回升。本文采用最小二乘法对其进行参数辨识。

图4 特定充电状态下某锂电池的电流与电压响应
3.2 仿真与分析
根据本文所建立的锂电池分数阶组抗模型以及所设计的分数阶卡尔曼滤波器,本文采用了Simulink仿真软件以及实验验证。
图5为UDDS工况下使用分数阶卡尔曼滤波器对锂电池的工作电压进行追踪,分析结果表明该滤波器可以有效地对锂电池的工作电压进行追踪,误差稳定在0.05 V以内。

(a)工作电压的参考值与估计值

(b)工作电压追踪误差图5 UDDS工况下工作电压追踪
图6为利用本文所设计的分数阶卡尔曼滤波器,在UDDS工况下,对初始充电状态未知(即存在初始误差)的锂电池充电状态进行追踪,结果表明该分数阶卡尔曼滤波器可以有效地追踪锂电池的充电状态,误差稳定在2%以内。

(a)充电状态的参考值与估计值
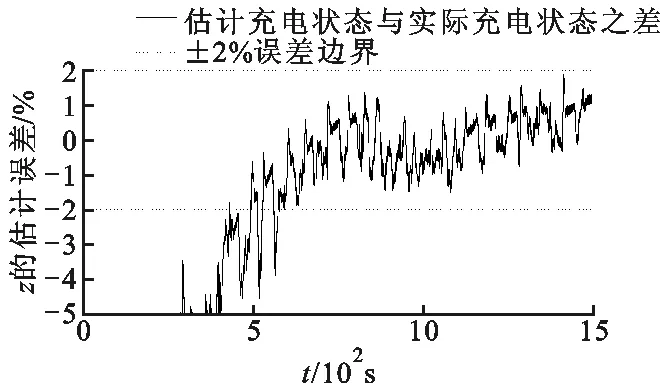
(b)充电状态的估计误差图6 UDDS工况下充电状态的估计
4 结 论
本文通过对锂电池电化学阻抗谱以及锂电池的HPPC脉冲响应进行分析,提出分数阶阻抗模型,利用最小二乘法对该阻抗模型进行参数辨识,设计分数阶卡尔曼滤波器对UDDS工况下锂电池的充电状态以及工作电压进行估计,该分数阶阻抗模型可准确预测锂电池的工作电压,误差在0.05 V以内,对初始充电状态未知的锂电池充电状态估计误差在2%以内,结果表明所建立的分数阶阻抗模型可以准确预测锂电池的充电状态,可为电动汽车动力电池管理系统提供有效的状态估计。
[1] 李哲. 纯电动汽车磷酸铁锂电池性能研究 [D]. 北京: 清华大学汽车工程系, 2011.
[2] 王丹, 续丹, 曹秉刚. 电动汽车关键技术发展综述 [J]. 中国工程科学, 2013, 15(1): 68-72. WANG Dan, XU Dan, CAO Binggang. Overview on key techniques of electric vehicle [J]. Engineering Sciences, 2013, 15(1): 68-72.
[3] ANDRE D, APPEL C, SOCZKA-GUTH T, et al. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries [J]. Journal of Power Sources, 2013, 224: 20-27.
[4] ZHANG Jingliang, LEE J. A review on prognostics and health monitoring of Li-ion battery [J]. Journal of Power Sources, 2011, 196(15): 6007-6014.
[5] SALKIND A J, FENNIE C, SINGH P, et al. Determination of state-of-charge and state-of-health of batteries by fuzzy logic methodology [J]. Journal of Power Sources, 1999, 80(1/2): 293-300.
[6] KOZLOWSKI J D. Electrochemical cell prognostics using online impedance measurements and model-based data fusion techniques [C]∥Proceedings of the 2003 IEEE Aerospace Conference. Piscataway, NJ, USA: IEEE, 2003: 3257-3270.
[7] HANSEN, T, WANG C J. Support vector based battery state of charge estimator [J]. Journal of Power Sources, 2005, 141(2): 351-358.
[8] BLANKE H, BOHLEN O, BULLER S, et al. Impedance measurements on lead-acid batteries for state-of-charge, state-of-health and cranking capability prognosis in electric and hybrid electric vehicles [J]. Journal of Power Sources, 2005, 144(2): 418-425.
[9] MACHADO J A T, GALHANO A. Fractional dynamics: a statistical perspective [J]. Journal of Computational and Nonlinear Dynamics, 2008, 3(4): 233-237.
[10]NG K S, MOO C S, CHEN Yiping, et al. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries [J]. Applied Energy, 2009, 86(9): 1506-1511.
[11]LI Xueyan, XIAO Meng, CHOE S Y. Reduced order model (ROM) of a pouch type lithium polymer battery based on electrochemical thermal principles for real time applications [J]. Electrochimica Acta, 2013, 97: 66-78.
[12]HE Hongwen, XIONG Rui, FAN Jinxin. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach [J]. Energies, 2011, 4(4): 582-598.
[13]BULLER S, THELE M, DE DONCKER R W A A, et al. Impedance-based simulation models of supercapacitors and Li-ion batteries for power electronic applications [J]. IEEE Transactions on Industry Applications, 2005, 41(3): 742-747.
[14]席安静. 磷酸铁锂电池电化学阻抗谱实验研究 [D]. 北京: 清华大学汽车工程系, 2012.
[15]XU Jun, MI C C, CAO Binggang, et al. A new method to estimate the state of charge of lithium-ion batteries based on the battery impedance model [J]. Journal of Power Sources, 2013, 233: 277-284.
[16]曹军义, 梁晋, 曹秉刚. 基于分数阶微积分的模糊分数阶控制器研究 [J]. 西安交通大学学报, 2005, 39(11): 1246-1249. CAO Junyi, LIANG Jin, CAO Binggang. Fuzzy fractional order controller based on fractional calculus [J]. Journal of Xi’an Jiaotong University, 2005, 39(11): 1246-1249.
[17]曹军义, 曹秉刚. 分数阶控制器离散方法的评估策略研究 [J]. 西安交通大学学报, 2007, 41(7): 842-846. CAO Junyi, CAO Binggang. Evaluation strategies of fractional order controllers discretization methods [J]. Journal of Xi’an Jiaotong University, 2007, 41(7): 842-846.
[18]LEITH D J, LEITHEAD W E. Survey of gain-scheduling analysis and design [J]. International Journal of Control, 2000, 73(11): 1001-1025.
[19]PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: part 1 Background [J]. Journal of Power Sources, 2004, 134(2): 252-261.
[20]PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: part 2 Modeling and identification [J]. Journal of Power Sources, 2004, 134(2): 262-276.
[21]PLETT G L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: part 3 State and parameter estimation [J]. Journal of Power Sources, 2004, 134(2): 277-292.
(编辑 武红江)
A Fractional Impedance Model for Charge State Estimation of Lithium Battery
YANG Qingxia1,CAO Binggang1,XU Jun1,LI Xiuqing2,NING Bo1,WANG Bin1
(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. School of Materials Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
A fractional impedance model based on the electrochemical impedance spectroscopy of lithium batteries is proposed to focus on the charge state estimation problem of the EV power lithium-ion batteries. A relatively simple equivalent circuit is derived from EIS analysis under different frequency and the introduction of fractional order modeling, and a fractional Kalman filter is designed according to the fractional impedance model. Parameters of the model are identified from the HPPC test data. The software SIMULINK is used to simulate the working voltage and charge state of the lithium battery and the simulation results are compared with test results. Comparison results show that the proposed model accurately predicts the working voltage, and its error range is within 0.05 V, and the charge state estimation has an error range of 2%. Results show that the fractional impedance model can accurately predict charge state of lithium batteries, and provides effective state estimations for EV power battery management system.
lithium battery state of charge; fractional impedance model; fractional Kalman filter
2015-01-18。 作者简介:杨晴霞(1988—),女,博士生;徐俊(通信作者),男,讲师。 基金项目:国家自然科学基金资助项目(51405374)。
时间:2015-05-21
10.7652/xjtuxb201508021
TM912.8
A
0253-987X(2015)08-0128-05
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150521.0901.001.html

