一种非线性双稳态人体运动能量俘获技术

王伟,曹军义,林京,周生喜,蔡云龙

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)



一种非线性双稳态人体运动能量俘获技术

王伟,曹军义,林京,周生喜,蔡云龙

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

针对传统线性压电悬臂梁频带过窄且难以与人体运动相匹配的问题,考虑人体小腿的运动特点,设计了一种双稳态磁耦合压电悬臂梁应用于人体运动能量俘获,利用运动过程中小腿的摆动及其与地面间的冲击产生的加速度使悬臂梁跨越势阱提高俘能效率。以哈密顿原理及人体运动信号为基础,建立了用于人体运动能量俘获的非线性动力学模型。根据人体腿部运动的振动特征设计了一种便携式非线性振动能量俘获系统,实现了线性、非线性单稳态和双稳态等动力学特征。采用实际腿部振动信号进行的理论模型数值仿真表明:双稳态人体振动俘能技术能够产生大幅度跨越势阱运动并俘获较多的电能。人体不同运动状态的实验结果验证了非线性双稳态人体能量俘获技术的优势以及所建立的机电耦合模型的有效性。当运动速度为8 km/h时,双稳态系统的平均功率达到最大值23.2 μW。

能量俘获;非线性;双稳态;人体运动;压电悬臂梁

随着低功耗通信技术和微电子技术的迅速发展,可穿戴式和便携式的嵌入式健康监测设备、微型传感器、人体网络定位装置等开始出现。然而,由于此类设备大多依赖电池供电,长期使用需要定期更换电池来维持,寻求可靠的能量来源为这些设备供电,减少其对外部电池的依赖性成为该领域研究的重要技术需求。因此,将人体运动产生的能量转换为电能的能量俘获技术获得了越来越广泛的关注。近年来,国内外学者研究人体运动能量俘获的方法主要有电磁式[1-2]、热电式[3]和压电式[4-5]等。压电式振动能量俘获装置因具有易于微型化、功率密度较高等特点,成为了人体振动能量俘获技术研究的焦点。

由于传统线性压电悬臂梁共振频带过窄,大量的科研工作者开始将非线性引入压电振动能量收集领域。McInnes提出利用非线性随机共振原理提高振动能量俘获效率,并利用拥有双稳态特性的物理模型,通过理论分析验证了该方法的有效性[6]。Erturk等设计了一种双稳态结构装置,基于Duffing方程和基尔霍夫定理,建立了压电磁耦合悬臂梁装置简化的动力学模型,并研究了压电磁耦合悬臂梁的非线性能量俘获特性[7-8]。曹树谦等建立了双稳态悬臂梁的磁力模型,并通过实验验证了该系统能够实现频带较宽的大振幅运动[9]。陈仲生等借鉴随机共振原理,研究发现双稳态压电悬臂梁在外部宽频随机振动激励下会产生随机共振现象,输出电压成倍增大[10]。Zhou等设计了一种旋转磁铁式磁耦合压电悬臂梁结构,通过旋转磁铁的调节来实现俘能频带的大幅提升,并且验证了引入非线性可以使俘能效率得到提高[11-13]。但是,以上研究均是基于理想的激励条件进行的,而关于非线性压电悬臂梁应用于复杂人体(小腿)运动的能量俘获技术研究还非常少。

在人体行走过程中,以一足(支撑足)为支点,另一足(运动足)绕髋部作近似圆周运动,此时髋部向前运动,且膝关节有弯曲运动。运动足的运动可简单描述如下:足跟抬起,足部用力向下向后,推动人体向前移动;运动足离地,向前作加速运动;运动足膝部弯曲,防止足部接触地面;运动足继续前行;运动足减速,落地。可见,单足的运动是一个不断加速、减速、绕髋部和膝关节摆动的周而复始的过程。在腿部的摆动过程中和运动足与地面接触的过程中,均有较大的冲击加速度产生。

本文考虑人体小腿的运动特点,设计了一种双稳态磁耦合压电悬臂梁应用于人体运动能量俘获,利用运动过程中小腿的摆动及其与地面间的冲击产生的加速度使悬臂梁跨越势阱提高俘能效率。设计了双稳态、线性单稳态和非线性单稳态3种悬臂梁结构进行实验对比,以验证双稳态磁耦合压电悬臂梁应用于人体运动能量俘获的优势。

1 非线性动力学模型

设计的磁耦合压电悬臂梁结构如图1a所示,其中外部磁铁的旋转角度α、间距dm和悬臂梁高度h均可调并且外部磁铁可拆卸,通过上述参数的调节,可以得到不同的非线性回复力,从而得到具有不同势阱的压电悬臂梁。

图1 压电俘能装置示意图

基于哈密顿原理,压电悬臂梁拉格朗日函数的变分VI在任何时间段t1、t2内应该恒为0,即有

(1)

式中:δ为变分符号;Ek、Ep、Ea分别为动能、势能、外部激励能。悬臂梁端部质量块变形微小,可将其视为集中质量,则式(1)中各量可表示为

(2)

式中:Vs、Vp分别为中间层体积、压电层体积;ρs、ρp分别为中间层密度、压电层密度;u为悬臂梁的挠度;mt是端部集中质量;Nf和Nq分别为作用在悬臂梁上的力的个数、电量的个数;fi(xi)为作用在xi处的力;v′、qj分别为作用在悬臂梁上的电压、电荷;S、T、D、E分别表示应变矢量、应力矢量、电位移矢量、电场强度矢量。经过整理可得图1a中磁耦合压电悬臂梁结构的机电耦合模型为

(3)

式中:M、C、θ分别表示等效质量、等效阻尼、等效机电耦合系数;Cp为压电材料PZT的等效电容;x(t)是悬臂梁端部的位移;R为负载电阻;V(t)为R两端电压;a(t)为外部激励加速度;Fr为悬臂梁的非线性回复力,在此采用多项式拟合方法将其表示为Fr=n0+n1x(t)+n2x(t)2+…+nnx(t)n,其中n0,n1,n2,…,nn表示多项式拟合系数。对Fr进行积分可以得到悬臂梁的势能函数U(x),即U(x)=∫Frdx。

2 实验设计与人体运动信号分析

2.1 实验设计

实验中,压电俘能装置如图1a所示,悬臂梁中间金属层材料为不锈钢,尺寸为95 mm×10 mm×0.27 mm,压电片是尺寸为12 mm×10 mm×0.6 mm的PZT-51,两片并联连接。装置中的所有磁铁均为铷铁硼永磁铁,悬臂梁端部磁铁尺寸为8 mm×6 mm×4 mm,外部磁铁直径为25 mm、厚度为5 mm。为了获得人体运动过程中腿部摆动和踏地冲击产生的加速度并以此作为后续仿真的外部激励信号a(t),用加速度传感器(CXL04 GP3)采集运动过程中小腿部位的加速度;通过外部磁铁的调节获得具有不同势阱的悬臂梁,悬臂梁末端的位移用激光位移传感器(HL-G1)测量,以研究人体运动过程中压电悬臂梁的非线性运动特征。具体实验设置如图1b所示,加速度传感器粘贴在俘能装置的根部,位移传感器用螺钉固定,压电悬臂梁的振动方向与小腿的摆动方向一致。当人体运动时,用示波器(见图1c)同步采集3路电压信号,再将电压信号转换为相应的加速度信号、位移信号和俘获的电压信号。实验中,人体在跑步机上运动,调节跑步机的速度vT,分别测试不同速度下的加速度信号和悬臂梁的俘能电压及末端位移。

为了研究人体运动的双稳态振动能量俘获技术优势,通过调节外部磁铁的位置参数,设计了线性单稳态(linear energy harvester, LEH)、非线性单稳态(mono-stable energy harvester, MEH)和双稳态(bi-stable energy harvester, BEH)3种悬臂梁结构进行对比。具体的结构参数如下:非线性单稳态梁dm=58 mm,h=17 mm,α=0°;双稳态梁dm=55 mm,h=15 mm,α=10°;俘能装置去除外部磁铁后即为线性单稳态梁。

在静态水平位置时,用高级数字测力计(M5-2)和测量台架数字位移套装(ES002)测量不同稳态下回复力随位移的变化关系,测量结果如图2所示。用多项式进行拟合得到不同稳态下悬臂梁的回复力曲线方程分别为:线性单稳态梁Fr1=24.8x;非线性单稳态梁Fr2=-5.49×108x5+1.56×105x3+26.09x;双稳态梁Fr3=-6.8×1011x7+3.12×108x5+6.16×104x3-9.635 3x。对各回复力方程进行积分,即可得到相应的势能函数U(x),如图3所示。

图2 不同稳态悬臂梁的回复力测量值

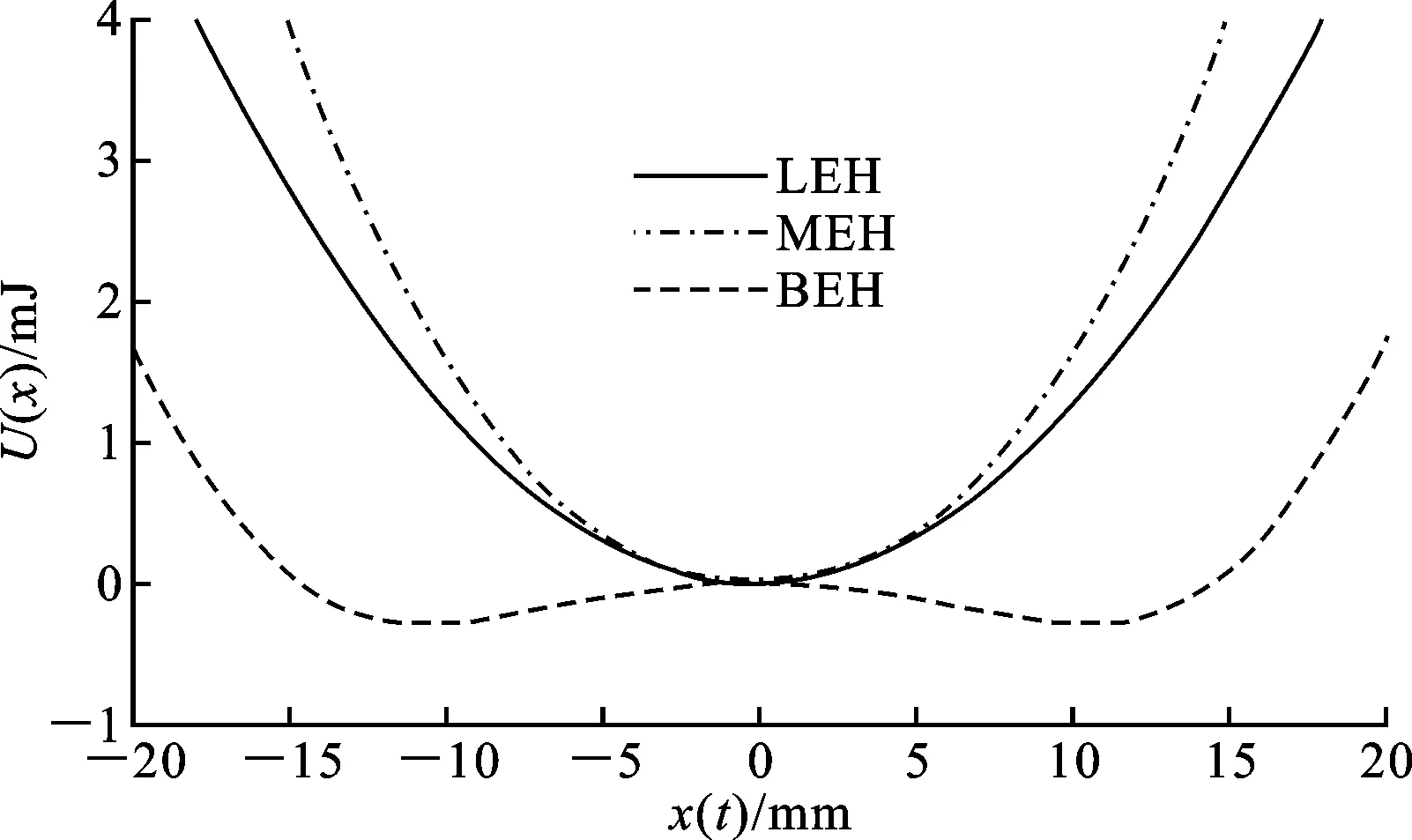
图3 不同稳态悬臂梁的势能曲线

2.2 人体运动信号分析

为研究人体的运动特征,采用前面设计的振动数据采集系统采集了不同对象(受试对象A,男性,身高175 cm,质量63 kg;对象B,男性,身高170 cm,质量73.5 kg)的运动信号。在不同运动速度下,实时采集的加速度随时间变化的关系及其频谱如图4所示。测量得到的加速度信号将作为仿真时机电模型的外部激励信号。

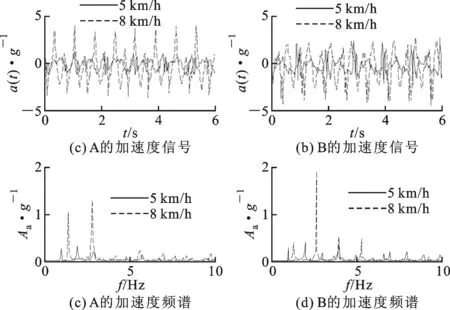
图4 不同运动速度下的加速度信号及其频谱

由图4可见,受试对象A和B小腿部位的加速度随着运动速度的增大而增大,最大值达到4g左右,表现出一定的不对称性;分析频谱图可以看出,随着运动速度增大,加速度的频率增大,且主要集中在人体运动的频率及其倍频处;在5km/h的速度下,受试对象A和B的运动频率为0.95Hz和1Hz,而在8km/h的速度下,受试对象A和B的运动频率为1.4Hz和1.3Hz,表现出一定的个体差异。人体的运动频谱主要集中在低频区域,目前低频的压电悬臂梁设计在微结构中实现比较困难。传统的线性压电悬臂梁主要采用机械共振的原理,在人体运动过程中,腿部的振动能量频带是随时间变化的,导致振动能量俘获的能力大大降低,因此本文设计了非线性双稳态压电悬臂梁,期望提高人体运动的振动能量俘获能力。

3 数值仿真

为了验证所建立的非线性机电耦合模型的有效性,在此利用受试对象A以5km/h的速度行走时采集到的加速度信号来进行数值仿真。仿真时机电模型中的电压V(t)和速度v(t)的初值设置为0,线性单稳态梁和非线性单稳态梁的位移初值设置为0,双稳态梁的位移初值设置为其势阱稳态点x0,悬臂梁的输出电压、端部位移、电压频谱、相轨迹被用来分析它们的俘能性能。

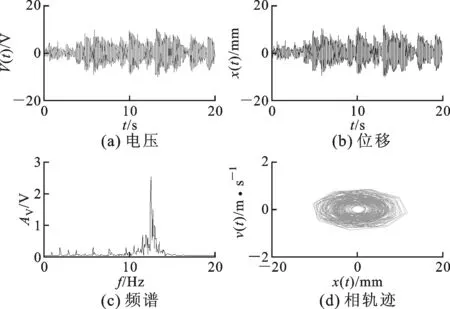
图5 线性单稳态梁仿真结果

图6 非线性单稳态梁仿真结果

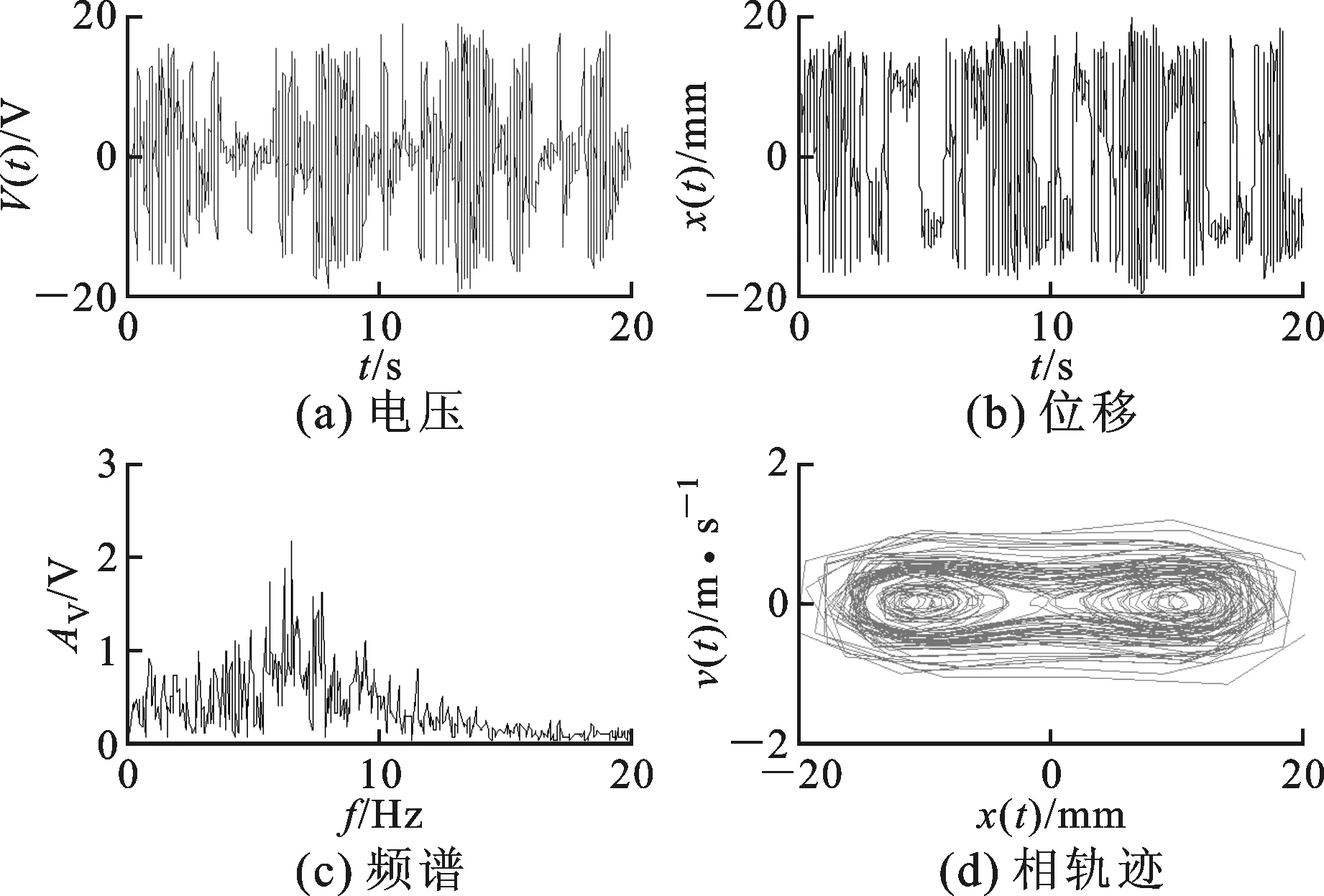
图7 双稳态梁仿真结果

线性单稳态、非线性单稳态和双稳态梁的仿真结果分别如图5、6、7所示。计算每种情况下电压绝对值的最大值和均方值,并考虑负载电阻R为10 MΩ,线性单稳态梁仿真结果的电压最大值为10.19 V,平均功率为1.3 μW;非线性单稳态梁电压的最大值为8.6 V,平均功率为0.73 μW,较线性单稳态梁有所降低;双稳态梁的俘能效率最高,其产生电压的最大值为19.5 V,平均功率为5.1 μW。

仿真结果表明,相较于线性单稳态梁,非线性单稳态梁产生较小的电压输出,其原因主要是由于调制的非线性单稳态梁具有较大的刚度,表现为硬特性,所以在相同的激励信号下其振幅较小。比较图6和图7的电压频谱图,线性单稳态梁的频率范围集中在12.55 Hz,而非线性单稳态梁的频率范围集中在13.95 Hz,较线性单稳态梁后移1.4 Hz,主要也是由于非线性单稳态梁的刚度较大造成的。双稳态梁相较于线性、非线性单稳态梁都具有更好的压电俘能效果,其功率输出提高了几倍,双稳态系统中非线性回复力的引入使悬臂梁的刚度变得很小,甚至在一定范围内出现负刚度,且双稳态系统有两个稳定平衡点,受到激励后悬臂梁端部会跨越势阱在这两个平衡点间做往复运动,使俘能效率提高。由电压频谱图可见,其频率范围主要集中在4～8 Hz,相较于线性单稳态和非线性单稳态梁频率出现明显的前移,主要是由于非线性磁力使悬臂梁刚度变小而引起的。

4 实验验证

实验中调节跑步机的速度,在不同运动速度下测试具有不同势阱的悬臂梁的压电俘能效果。选择受试对象A在速度为5 km/h(走路)和8 km/h(跑步)两种情况下作对比说明。线性单稳态、非线性单稳态、双稳态梁在两种速度下产生的电压V(t)及其频谱分别如图8、9、10所示。

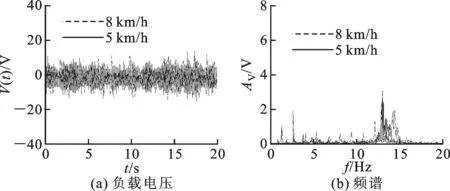
图8 不同运动速度下线性单稳态梁的实验结果

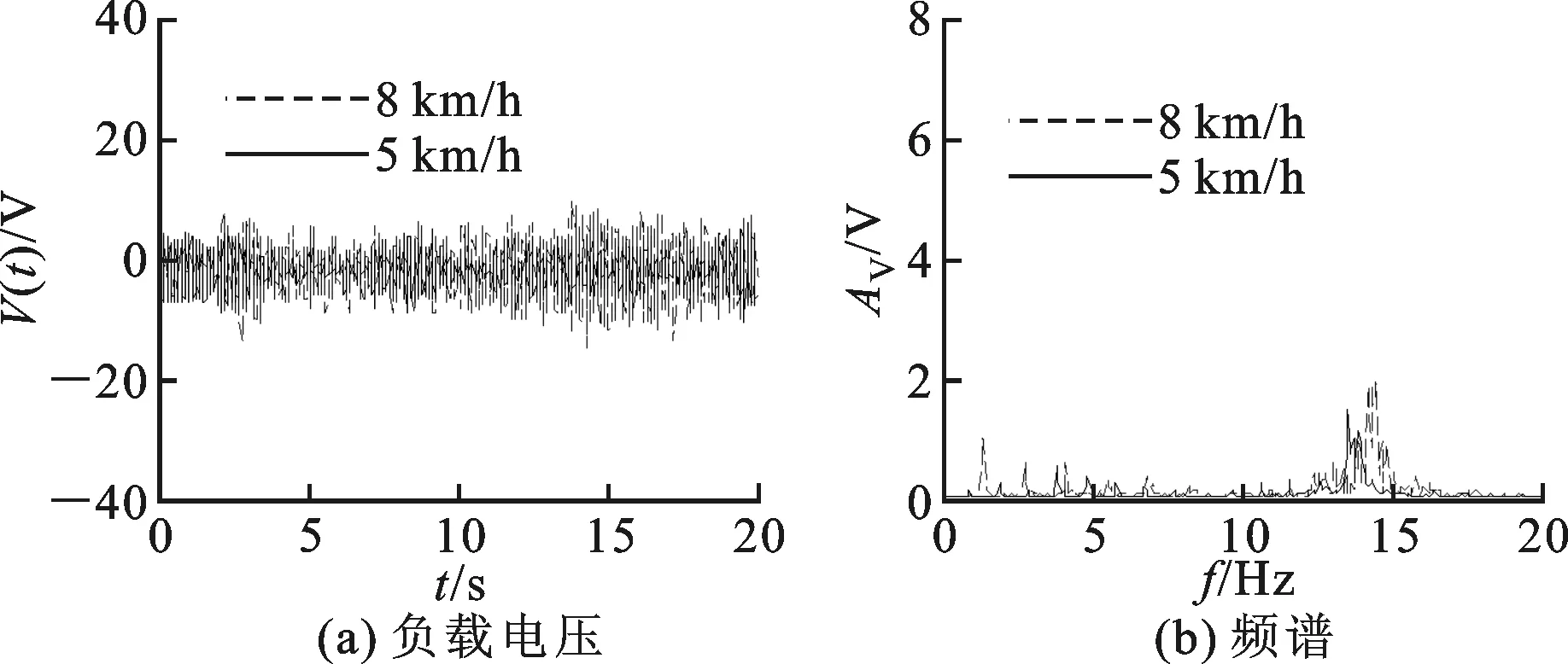
图9 不同运动速度下非线性单稳态梁的实验结果

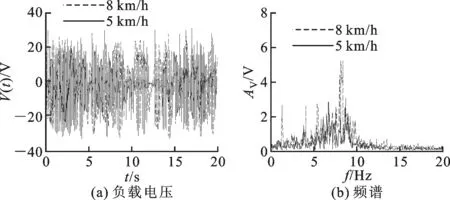
图10 不同运动速度下双稳态梁的实验结果

当运动速度为5 km/h时,线性单稳态梁产生电压的最大值为11.25 V,平均功率为1.57 μW,当运动速度为8 km/h时,电压的最大值为16.1 V,平均功率为2.47 μW,速度增大,俘能效率提高;非线性单稳态梁在运动速度为5 km/h时,产生电压的最大值为10.7 V,平均功率为0.98 μW,运动速度为8 km/h时,电压的最大值为14.8 V,平均功率为2.033 μW,非线性单稳态梁较线性单稳态梁效率有所下降;俘能效果最好的双稳态梁在5 km/h时,产生电压的最大值为27.9 V,平均功率为7.21 μW,8 km/h情况下电压的最大值为33.7 V,平均功率为18.1 μW。将实验结果与仿真进行对比,在一定程度上验证了所建立的机电模型的有效性。

实验中调节位移传感器的激光点与悬臂梁末端的距离为15 mm,在8 km/h的运动速度下,3种稳态下悬臂梁的位移信号及其对应的位移-电压相图如图11所示。综合比较图8～11可以看出,与双稳态梁相比,单稳态梁不能跨越势阱产生阱间大幅振荡,所以在相同的运动速度下,产生的电压较小。分析线性单稳态梁的频谱图可以看出其频率集中范围基本相同,均在其固有频率12.75 Hz附近,另外从频谱图上可以看出,在运动频率及其倍频处存在一定的峰值,可以认为是悬臂梁在受到冲击后以其固有频率做自由振动。而实验中的非线性单稳态梁的运动规律基本与线性单稳态梁相似,但是由于其刚度较大,所以其频率集中范围(13.85 Hz)较线性单稳态梁右移,悬臂梁末端的位移也较线性单稳态梁小。而双稳态梁在运动过程中由于小腿的摆动及其与地面间的冲击作用跨越势阱做阱间大幅震动以致产生高电压,且由于速度的增大,双稳态梁跨越势阱更为频繁,所以在较大运动速度下产生的电能输出更大。

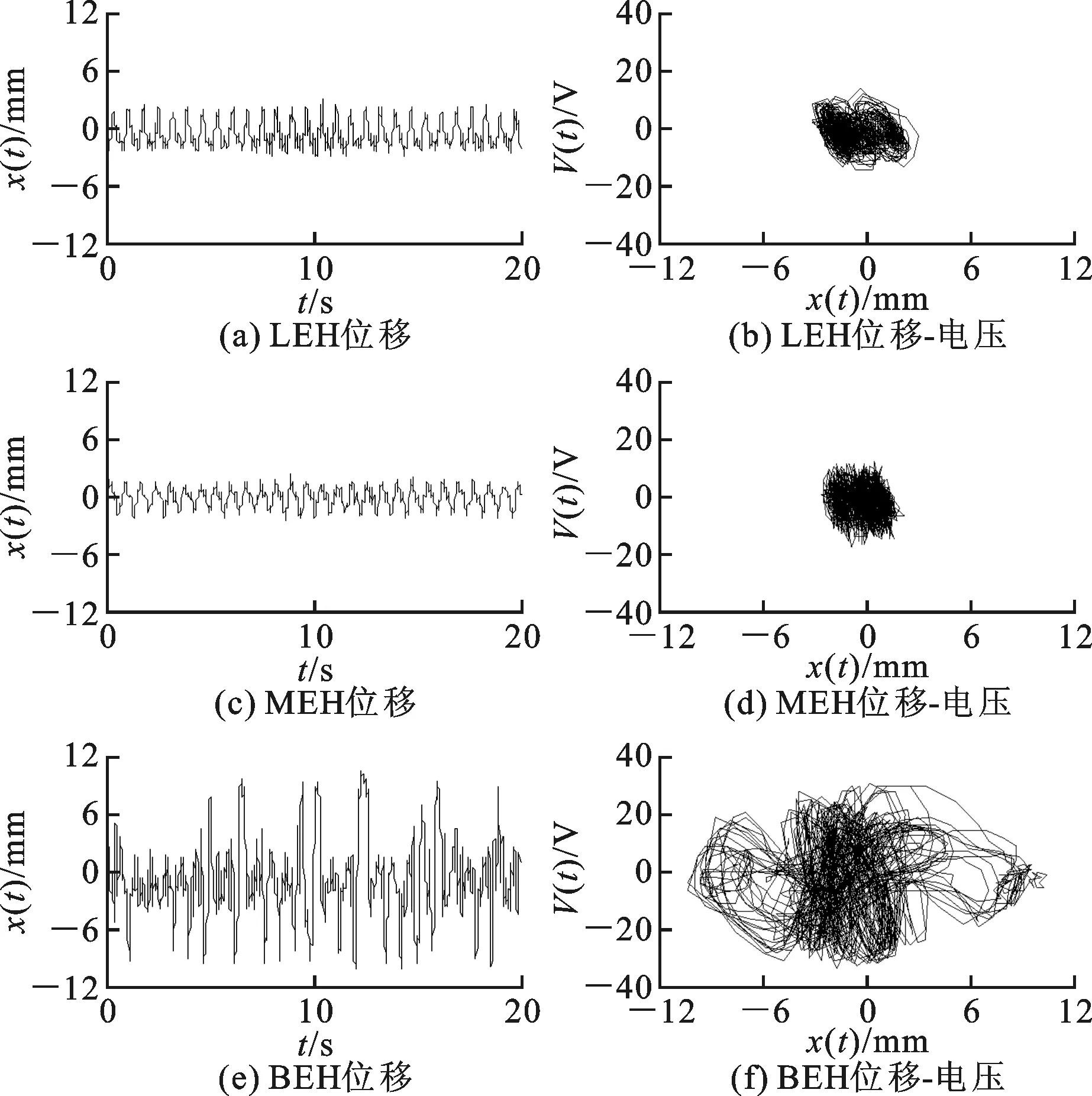
图11 3种稳态在8 km/h下的实验结果

实验中在每种稳态下,分别对受试对象A和B在不同运动速度下进行测试,不同速度情况下的输出功率P如图12所示。由图可见,在相同的稳态下,随着运动速度的增大,输出功率有增大的趋势,且受试对象A和B存在一定的差异;在相同的运动速度下,由于非线性单稳态梁刚度较大,所以其相较于线性单稳态梁有较小的输出功率,而双稳态梁的输出功率最大;在运动速度为8 km/h时,受试对象B的输出功率最大,达到23.2 μW。

图12 不同运动速度下的输出功率

5 结 论

本文提出了一种基于非线性双稳态的人体运动能量俘获技术,并根据人体的运动信号及哈密顿原理等建立了具有非线性双稳态压电悬臂梁的动力学模型。通过数值仿真和实验研究,可以得到以下结论。

(1)所建立的非线性机电耦合模型应用于人体运动能量俘获时,在一定程度上可反映非线性悬臂梁的振动俘能性能及其动力学特征。

(2)在人体运动过程中,非线性双稳态悬臂梁由于小腿的摆动及其与地面间的冲击而跨越势阱产生阱间大幅高能运动,所以其俘能效率较线性、非线性单稳态悬臂梁均有大幅提高。

[1] ROME L C, FLYNN L, GOLDMAN E M, et al. Generating electricity while walking with loads [J]. Science, 2005, 309(5741): 1725-1728.

[2] SAHA C R, O’DONNELL T, WANG N, et al. Electromagnetic generator for harvesting energy from human motion [J]. Sensors and Actuators: A Physical, 2008, 147(1): 248-253.

[3] KIM M K, KIM M S, LEE S, et al. Wearable thermoelectric generator for harvesting human body heat energy [J]. Smart Materials and Structures, 2014, 23(10): 105002.

[4] LEFEUVRE E, BADEL A, RICHAARD C, et al. Energy harvesting using piezoelectric materials: case of random vibrations [J]. Journal of Electroceramics, 2007, 19(4): 349-355.

[5] ZHAO Jingjing, YOU Zheng. A shoe-embedded piezoelectric energy harvester for wearable sensors [J]. Sensors, 2014, 14(7): 12497-12510.

[6] MCINNES C R, GORMAN D G, CARTMELL M P. Enhanced vibrational energy harvesting using nonlinear stochastic resonance [J]. Journal of Sound and Vibration, 2008, 318(4/5): 655-662.

[7] ERTURK A, HOFFMANN J, INMAN D J. A piezomagnetoelastic structure for broadband vibration energy harvesting [J]. Applied Physics Letters, 2009, 94(25): 2-3.

[8] ERTURK A, INMAN D J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling [J]. Journal of Sound and Vibration, 2011, 330(10): 2339-2353.

[9] 孙舒, 曹树谦. 双稳态压电悬臂梁发电系统的动力学建模及分析 [J]. 物理学报, 2012, 61(21): 95-106. SUN Shu, CAO Shuqian. Dynamic modeling and analysis of a bistable piezoelectric cantilever power generation system [J]. Acta Physica Sinica, 2012, 61(21): 95-106.

[10]陈仲生, 杨拥民. 悬臂梁压电振子宽带低频振动能量俘获的随机共振机理研究 [J]. 物理学报, 2011, 60(7): 437-443. CHEN Zhongsheng, YANG Yongmin. Stochastic resonance mechanism for wideband and low frequency vibration energy harvesting based on piezoelectric cantilever beams [J]. Acta Physica Sinica, 2011, 60(7): 437-443.

[11]ZHOU Shengxi, CAO Junyi, LIN Jing, et al. Exploitation of a tristable nonlinear oscillator for improving broadband vibration energy harvesting [J]. The European Physical Journal Applied Physics, 2014, 67(3): 30902.

[12]ZHOU Shengxi, CAO Junyi, INMAN D J, et al. Broadband tristable energy harvester: modeling and experiment verification [J]. Applied Energy, 2014, 133: 33-39.

[13]周生喜, 曹军义, ERTURK A, 等. 压电磁耦合振动能量俘获系统的非线性模型研究 [J]. 西安交通大学学报, 2014, 48(1): 106-111. ZHOU Shengxi, CAO Junyi, ERTURK A, et al. Nonlinear model for piezoelectric energy harvester with magnetic coupling [J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 106-111.

(编辑 武红江)

Nonlinear Bi-Stable Energy Harvester from Human Motion

WANG Wei,CAO Junyi,LIN Jing,ZHOU Shengxi,CAI Yunlong

(State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A nonlinear bi-stable energy harvester from the human motion is proposed to solve the problem that the frequency bandwidth of traditional linear piezoelectric energy harvesters is narrow and it is hard to match with human motions. The harvester considers the characteristics of the human leg’s motion and improves the energy harvesting efficiency by using the acceleration caused by leg swings and their impacts on the ground. An electromechanical model of nonlinear energy harvesters is derived based on the Hamilton principle and human motion signals. A portable nonlinear energy harvesting device is designed based on the characteristics of the human motion, and dynamic characteristics of linear, nonlinear mono-stable and bi-stable oscillators are realized by adjusting the position of magnets. Numerical simulations based on real human leg’s vibration data show that the proposed harvester achieves the large amplitude inter-well oscillation and generates more energy from the human motion. Experimental results under various motion speeds verify the great advantage of the nonlinear bi-stable energy capture technology, and the efficiency of the proposed electromechanical model. The average output power of the bi-stable system reaches a maximum value of 23.2 μW when the motion speed is 8 km/h.

energy harvesting; nonlinear; bi-stable; human motion; piezoelectric cantilever

2015-03-31。 作者简介:王伟(1990—),男,硕士生;曹军义(通信作者),男,副教授。 基金项目:国家自然科学基金资助项目(51421004);新世纪优秀人才支持计划资助项目(NCET-12-0453)。

时间:2015-07-17

10.7652/xjtuxb201508010

TH39

A

0253-987X(2015)08-0058-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150717.1718.006.html