面向运动平稳性的直线电机推力频谱特征分析
马成方,杨晓君,张俊,吕盾,赵万华
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安)
面向运动平稳性的直线电机推力频谱特征分析
马成方1,2,杨晓君1,2,张俊1,2,吕盾1,2,赵万华1,2
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安)
针对直线电机推力谐波直接作用于驱动部件会降低进给系统运动平稳性的问题,综合考虑伺服驱动电路和电机结构非线性,利用等效磁化电流法和麦克斯韦方程,得到了纹波力、齿槽力、端部力、齿槽效应与电流谐波耦合力以及电感不对称力等5部分推力谐波的解析表达式。计算过程考虑了多个谐波因素之间的耦合作用,弥补了以往单一因素分析直线电机推力谐波的不足。研究结果表明:受驱动电路和电机结构非线性的影响,直线电机推力夹杂有众多的谐波成分,而且各个谐波成分之间相互耦合;这些推力谐波直接作用于机械系统,会造成进给系统显著的位移波动;随着进给速度的增加,推力谐波影响增大,尤其在进给速度为5、20和33 m/min附近,推力谐波激起了机械系统共振,位移波动急剧增大;纹波推力幅值随着驱动电流谐波幅值的减小而减小;电机的极距与齿槽距之比、齿槽开口与齿槽距之比,对于齿槽力的主要谐波阶次以及幅值都有重要影响,尤其当齿槽开口与齿槽距之比为0.625时,齿槽力各阶次谐波均为0。
直线电机;推力谐波;运动平稳性;系统共振
近些年来,直线电机进给系统由于取消了中间传动环节,具有进给速度高、推力大、没有反向间隙、刚度高等优点,逐步在高速数控机床上得到了广泛推广和应用[1]。随着研究的深入,直线电机中存在的诸多问题也显现出来,其中最受关注的是推力波动现象,它会引起动子速度的波动,使电机产生振动和噪声,甚至引起共振,严重影响进给系统的运动平稳性。作者团队前期的研究工作发现,直线电机进给系统的零传动结构使推力波动对运动平稳性的影响凸显[2-3]。
对于推力波动的机理和影响因素以往都有大量的分析研究,造成直线电机推力波动的主要因素,除了旋转电机中的气隙纹波磁场、齿槽效应以外,还有其所特有的端部效应。
针对纹波推力的研究,文献[4]在不考虑电流输入的前提下建立了永磁体气隙磁场模型;文献[5]采用谱分析发现推力波动的主要频率与谐波成分,谐波成分主要是6倍基频谐波;文献[6]考虑了电磁力谐波,使用因果顺序图(COG)对永磁直线同步电机(PMLSM)进行建模;文献[7]利用单一下山法对推力波动近似建立了推力波动模型。在以上的研究工作中,分析过程复杂,解析建模没有考虑电流谐波的产生机理,而且没有考虑齿槽效应对纹波推力的影响。
针对齿槽效应的研究,文献[8-9]利用麦克斯韦张量法建立了气隙磁场解析模型;文献[10]利用保角变换建立了齿槽力模型,分析了电机参数对齿槽力的影响;文献[11]利用麦克斯韦张量法,得到了考虑齿槽效应的多齿力矩模型。以上的分析工作主要考虑了电机结构对齿槽力的影响,而对于通电状态下的齿槽效应还鲜有研究。
直线电机所特有的端部效应,也受到了学者的广泛关注,文献[12-14]分析了电机参数与端部力的关系,通过优化电机结构进行改善;文献[15-16]利用磁场的连续性,分段建立了端部磁感应强度,并引入比例系数描述端部效应,通过建立新的等效电路对其进行了分析;文献[17]利用等效磁化电流法建立了直线电机的气隙磁场模型,并通过许-克变换考虑端部效应对气隙磁场的影响。以上研究工作主要集中于气隙磁场,得到的端部力表达式复杂,多数通过数值解进行分析。
此外,在次级磁场作用下,电机的初级电感会产生饱和与畸变现象,其波动规律与电机初级位置(电角度)相关;另一方面,直线电机绕组不对称,由于漏磁的存在,位于电机端部的两相绕组电感的均值与中间一相绕组不相等。这样由于电感的饱和与不对称,也会造成直线电机的推力波动。
以上研究工作的分析偏重于直线电机本身,将各个因素单独分析,没有考虑多因素作用下推力谐波对数控机床整机运动平稳性的影响。考虑到实际的进给系统包含多阶模态,机械系统的动态特性随不同的位置、速度、加速度会发生变化,一旦某一阶推力谐波分量与机械系统的某一阶固有频率相接近而引发共振,将严重降低进给系统的运动平稳性。
本文综合考虑了伺服中存在的众多非线性因素,利用等效磁化电流法和麦克斯韦方程建立了表征推力谐波特性的频谱特征关系,并利用实验验证了理论分析。
1 多因素耦合下的推力频谱特征分析
1.1 综合考虑齿槽效应和端部效应的永磁体气隙磁场分析
依照文献[17]中的条件假设,不考虑齿槽效应和端部效应,直线电机的气隙磁场分析模型如图1所示。
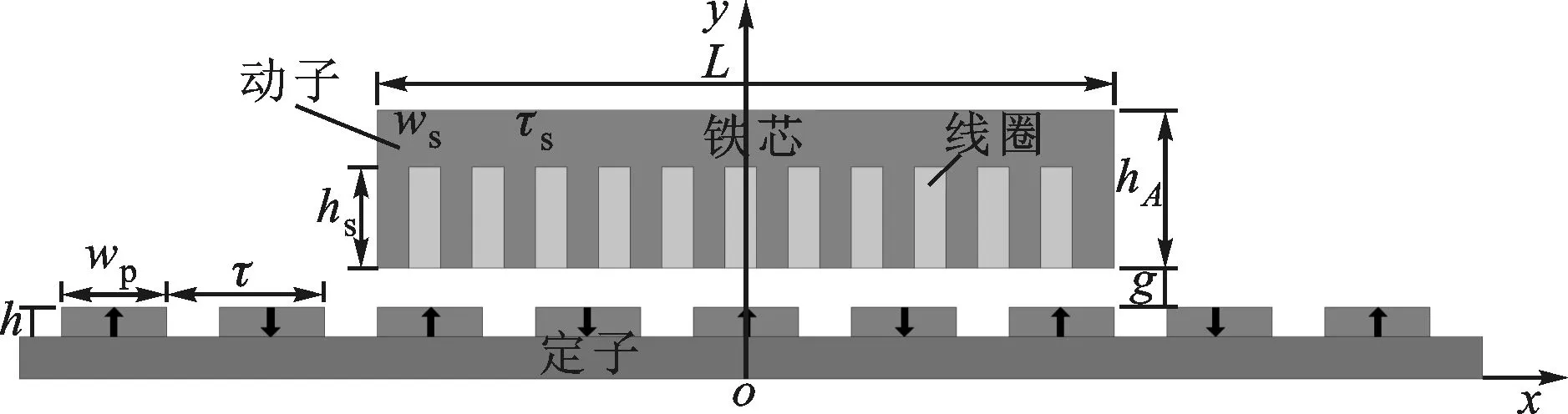
图1 永磁体磁场分析模型
在图1所示的解析区域中,根据麦克斯韦方程组对矢量磁位A建立磁场方程,永磁体区为
(1)
气隙区为
(2)
式中:A(x,y)是矢量磁位的z轴分量;μ0为磁导率;Jm(x)为永磁体的等效磁化电流密度。
通过对各区域的边界施加关于磁场强度的切向分量和法向分量的边界条件,求解永磁体产生的磁场强度[17]
(3)
由于直线电机中永磁体磁场的切向分量远小于法向分量,因此气隙磁场可仅考虑By。
引入气隙相对磁导函数,考虑电机的齿槽效应和端部效应,运用许-克变换建立分析模型,得到电机铁芯槽的气隙相对磁导函数为[8]
(4)
考虑端部效应时,永磁体产生的磁场的气隙相对磁导函数为[17]
式中:L为动子铁芯长度;g′=g+h/μr,h为永磁体高度,μr为磁导率。
综上可得,考虑了齿槽效应和端部效应的永磁同步直线电机气隙磁场模型为
(6)
1.2 综合考虑电路非线性与反馈控制的伺服输出电流特性分析
以a相为例,电路中各类非线性因素的影响最终作用到电机线圈上的电压谐波为
(7)
式中:usa、uka、Ema分别是由于电路调制、死区以及反电动势产生的谐波电压;v为进给速度。b、c相分别滞后a相2π/3、4π/3。
将电压谐波以干扰的形式作用到电流环,电流环采用PI控制,其中PWM简化为惯性环节,电流环控制框图如图2所示。

图2 电流环控制框图
利用拉氏逆变换,得到最终通过电流环产生的输出电流为
(8)
式中:T∑=Tpwm+Tg。
式(8)是考虑电流环控制作用下的驱动输出电流,为了简化公式,假设电机的三相线圈为无中线的星型连接,无三倍频谐波。取电流的初始相位为0,不考虑指令电流中的谐波成分,主要讨论电流谐波的稳态分量,则最终输出的三相电流为
(9)
1.3 推力的频谱特征表达
利用能量法可得直线电机的推力公式为
F=∑(Elf+Emf)if/v,f为a,b,c
(10)
式中:Elf、Emf分别为三相线圈的电枢反电势与空载反电势,以a相为例,即
(11)
(12)
b、c相分别滞后a相2π/3、4π/3。
忽略线圈自感以及互感的谐波成分,将前面的分析结果分别带入式(10),最后求解可得直线电机的推力为F=F0+Fr+Fc+Fe+Fq
(13)
式中:F0是名义推力;Fr是纹波推力,即
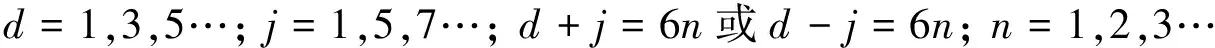
(14)
Fc是齿槽力,即
(15)
Fe是端部力,即
(16)
Fq是齿槽效应和初级电枢共同产生的波动推力,即
Fq=
(17)
式(14)~式(17)中相关量表达式如下
其中L、HA、h、g、τ、wp、τs和ws分别是动子长度、动子高度、永磁体厚度、气隙厚度、电机极距、永磁体宽度、齿距以及齿槽距。
前面在进行直线电机推力分析计算的时候,忽略了电感的高次谐波,但是实际中,在次级磁场作用下,电机的初级电感会产生饱和与畸变现象,其波动规律与电机初级位置(电角度)相关[18-19]。另外,直线电机绕组不对称,由于存在漏磁,位于电机端部的两相绕组电感的均值与中间一相绕组不相等。
为了简化计算过程,取各项电流的基波分量并不考虑初始相位,将设Ima=Imb=Imc=Im,则伺服驱动电路输出的三相电流为
(18)
考虑谐波特性的三相电感为
Laa=Laa0+Laa2cos2θ+Laa4cos4θ+…
(19)
(20)
(21)
将式(19)~式(21)带入式(10),整理可得由于电感非线性造成的新增加的直线电机推力谐波为
(22)
所以,由于电感非线性谐波的影响,直线电机会产生电流基频的6倍频谐波。
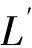
(23)
由上可得,考虑电机电感特性,会在直线电机的推力波动中增加两部分的谐波:一部分是由于电机电感非线性引起的电流基频的6倍频谐波;另一部分是由于直线电机两端开端造成电感不相等引起的2次谐波。第二种谐波为主要成分。
2 实 验
2.1 实验平台与实验方法
实验测试是在一台自主研制的高速高精5轴加工中心进行的,该机床X轴采用海德汉直线电机驱动,反馈元件采用海德汉的封闭式高精直线光栅,最大进给速度为90 m/min,最大加速度为15 m/s2,所用直线电机的主要结构参数如表1所示。

表1 直线电机主要结构参数
本次测试选取X轴为研究对象,X轴空载来回往复运动,采集不同速度下的电机推力数据和位移数据。利用海德汉数控系统的自带监测功能,监测运动过程中的推力数据(采样频率为10kHz),同时利用激光干涉仪采集主轴头处的位移数据(采样频率为10kHz),实验平台如图3所示。

图3 实验测试分析平台
2.2 实验结果与讨论
取进给速度为15m/min下匀速段的采集数据,对得到的推力以及位移数据分别进行分析,得到图4所示的时域图和图5所示的频域图。
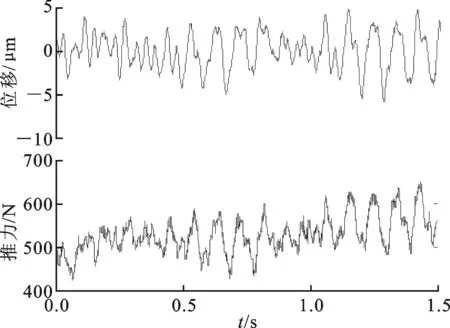
图4 15 m/min下匀速段位移波动与推力波动时域图
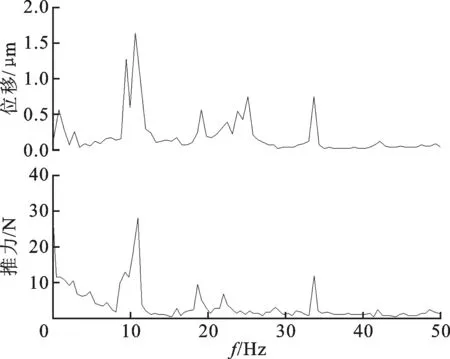
图5 15 m/min下匀速段位移波动频谱与推力波动频谱
从图4和图5中可以看到,电机推力不是一个恒定的名义力,其包含了多阶谐波成分,这些谐波推力会造成进给系统的位移波动。图5中的位移波动频谱成分与推力谐波成分的频率是一一对应的,说明位移波动是由谐波推力造成的。
将图5中15m/min速度下的各谐波力的频率实验值与理论值进行对比,结果如表2所示。从表2中可以看到,实验结果与前文所建立的推力谐波解析表达式吻合良好,最大偏差为5.44%。从图4中可以看到,谐波力造成的整体位移波动不可忽略,有必要面向进给系统的运动平稳性,全面分析多因素作用下直线电机推力谐波对进给系统运动平稳性的影响规律。

表2 推力波动频谱分析
采集不同速度下的电机推力数据和位移数据,得到电机推力各谐波分量随进给速度的变化规律如图6所示,位移波动随进给速度的变化规律如图7所示,其中位移波动值取各速度下的位移波动平均值。
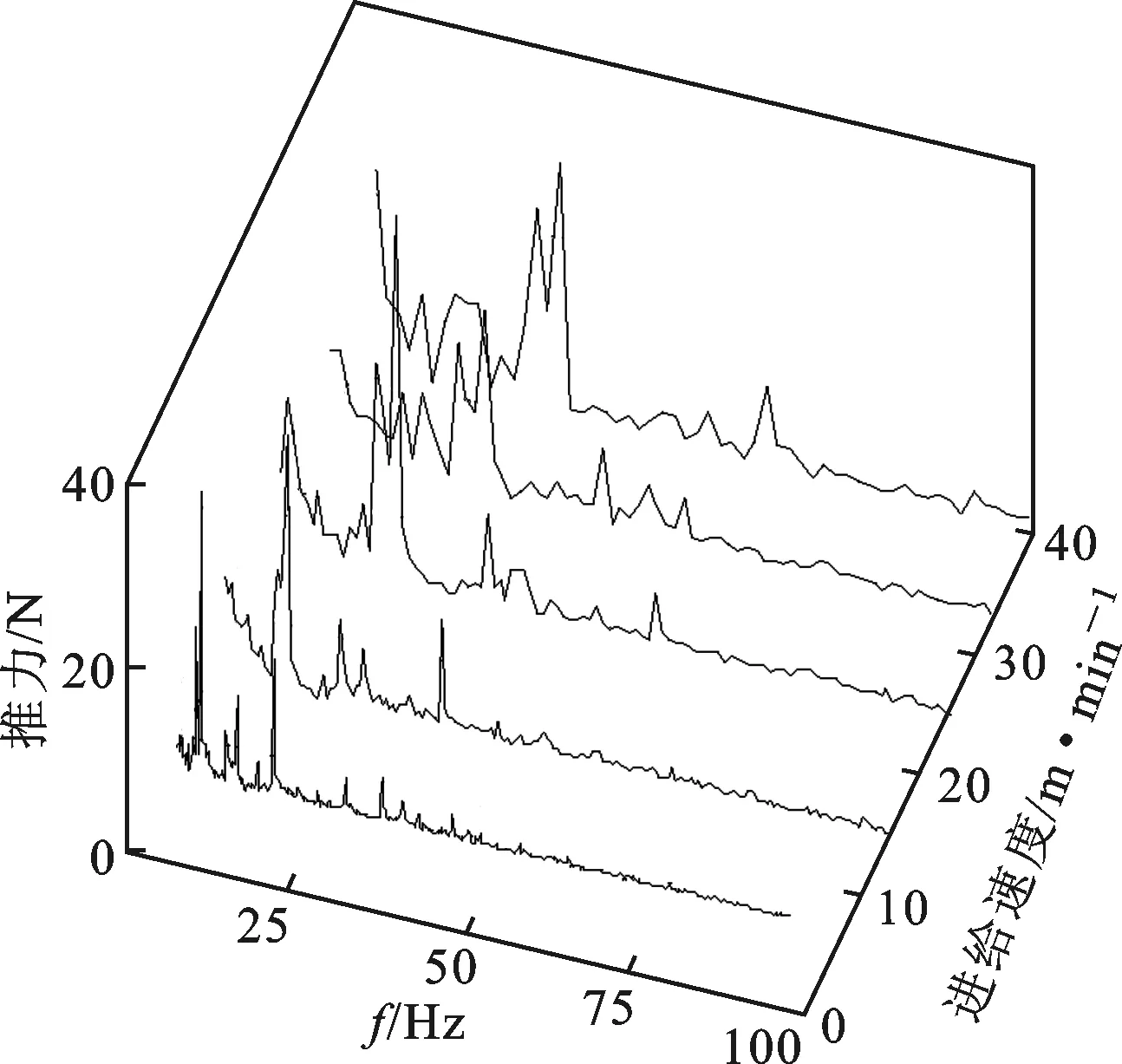
图6 电机推力各谐波分量随进给速度的变化规律
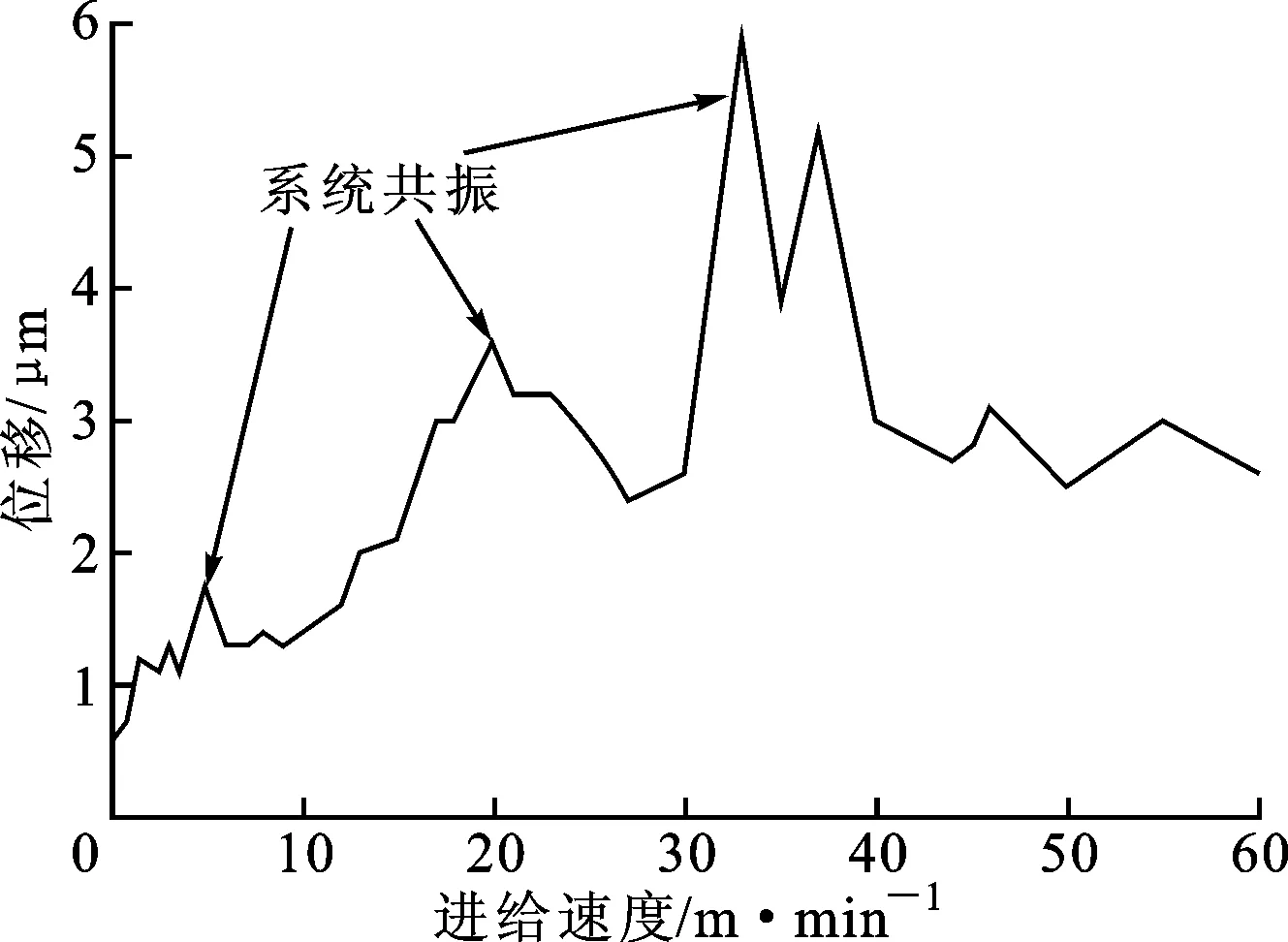
图7 位移波动随进给速度的变化规律
如图6所示,随着进给速度的变化,电机推力各谐波分量频率是不断变化的,虽然各谐波分量的幅值较小,但当变化过程中推力的某一谐波分量频率与机械系统的某一阶固有频率接近时,就会引起机械系统共振,严重降低进给系统的运动平稳性,如图7所示,在进给速度变化过程中出现了3处共振点。为了进一步说明这一共振现象,将不同速度下的位移波动进行快速傅里叶分析,分别以进给速度和谐波频率为横坐标绘图,如图8和图9所示。
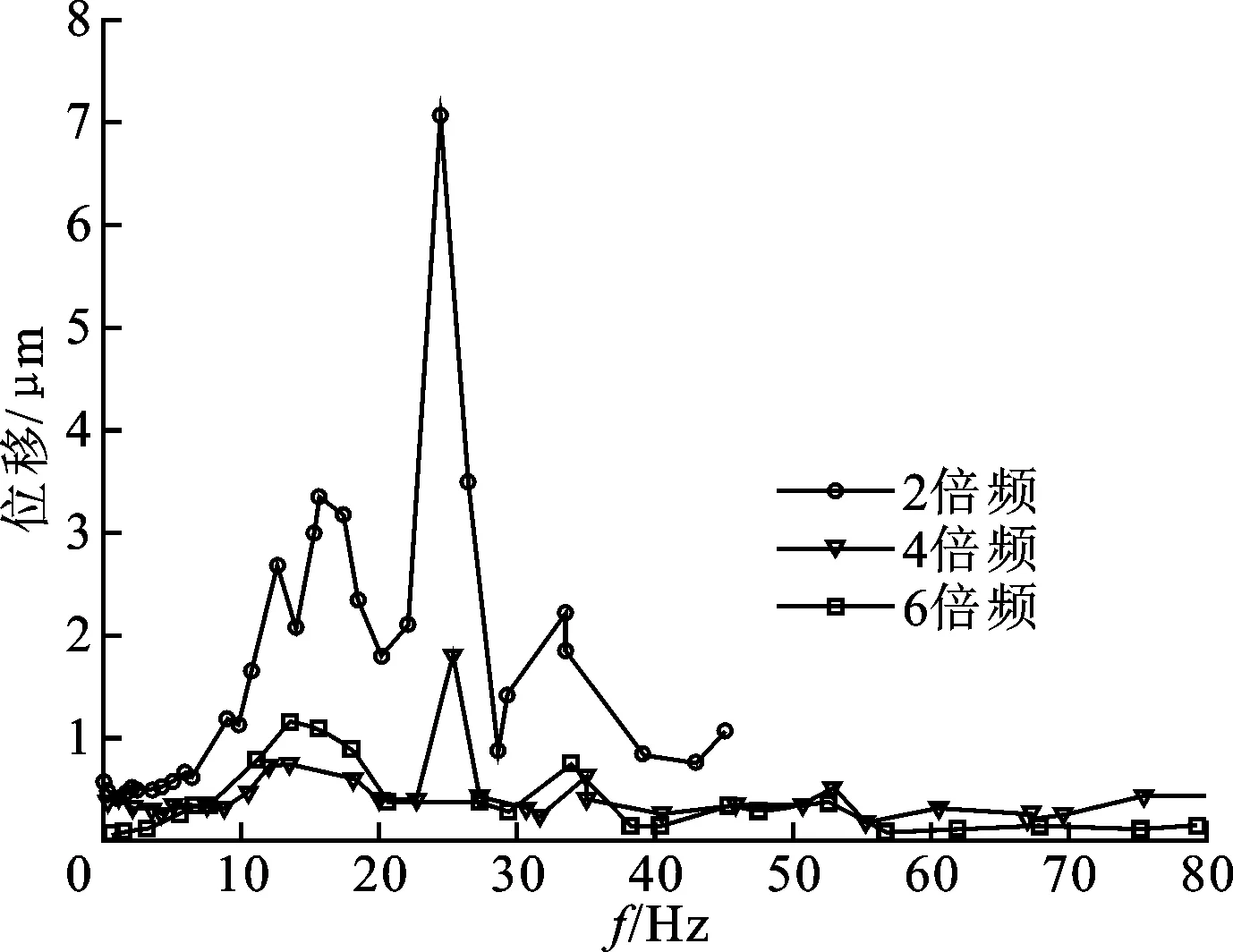
图8 位移波动随频率变化规律
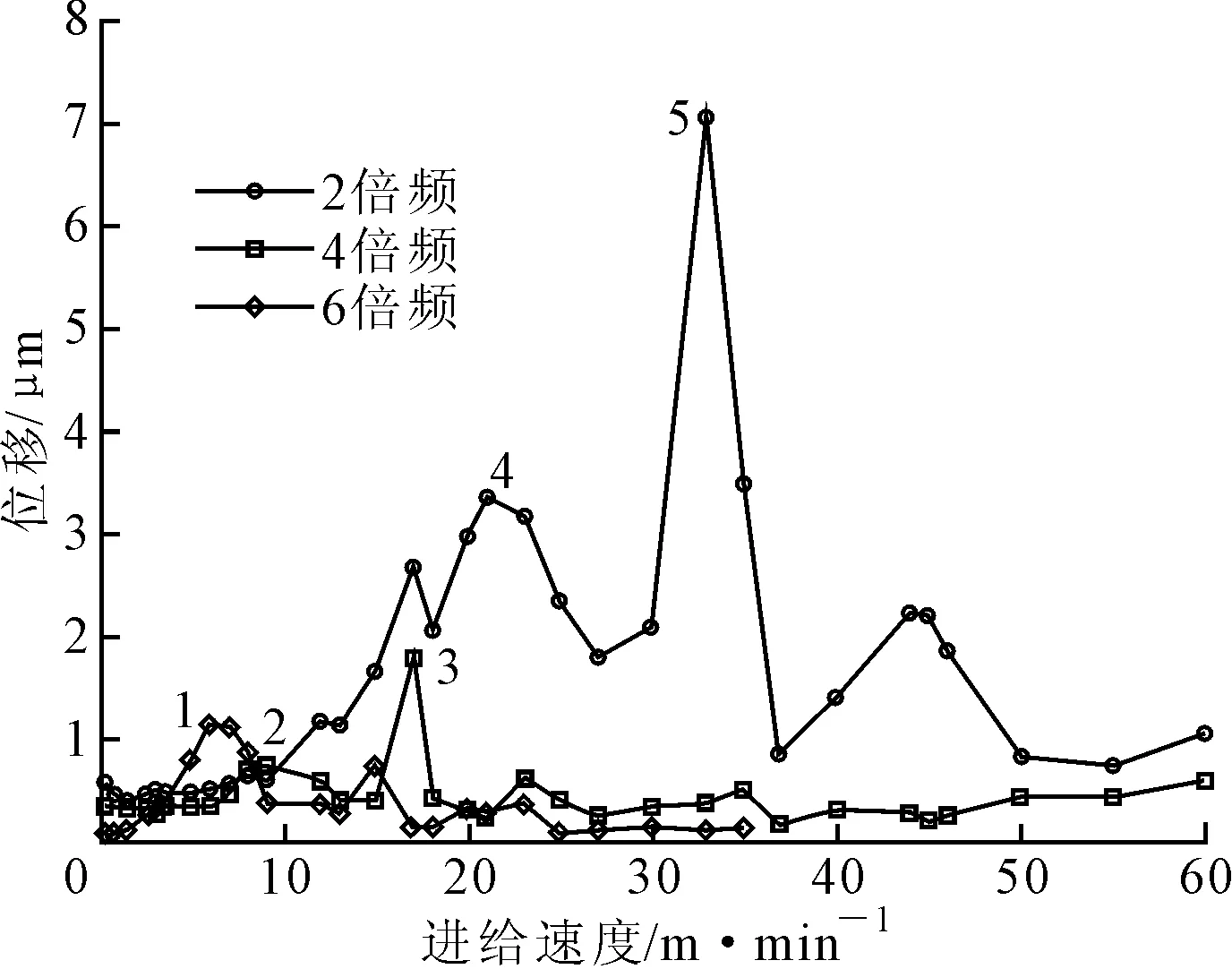
图9 位移波动随速度变化规律
不同的进给速度对应的电流基频不同,其所对应的2、4和6倍频谐波频率也就不同。从图8中可以看到,2、4和6倍频谐波力都是在15Hz和25Hz附近引起的位移波动幅值较大,说明在这两个频率附近引起了系统共振,共振幅值不同是由于不同倍频谐波力的幅值造成的。
图9可以看作是将图7中的位移波动进行了快速傅里叶分析。结合两图可以看到:低速时电流基频小,谐波力频率小于系统共振频率,没有激起共振;随着进给速度的增加,6倍频谐波频率首先接近15Hz左右,激起系统共振(图9中1点);随着进给速度的进一步增加,不同倍频谐波力依次接近系统固有频率引起系统共振,如图9中2、3、4和5点所示。
3 改善措施
对于纹波推力,主要是由于注入电机的驱动电流夹杂了高频谐波,而且由式(14)可得,纹波推力的幅值与驱动电流有密切的关系,随着驱动电流谐波的幅值减小,纹波推力迅速降低,但是纹波推力谐波的频率并不变化,如图10所示。因此,可以通过优化伺服驱动电路、调试电流环控制参数、设计先进控制补偿策略来减小电流谐波,降低纹波推力。
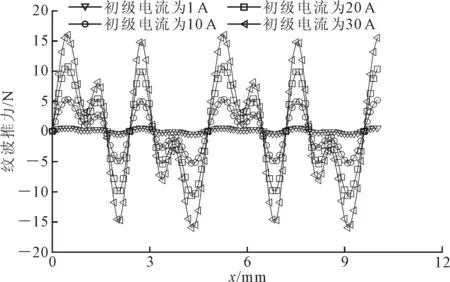
图10 初级电流对纹波推力的影响
对于齿槽效应的影响,由式(15)可得,除了直接的单一因素结构优化,电机结构参数中有两个比例系数对齿槽力有重要的影响,如图11、图12所示。
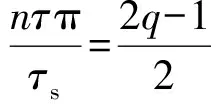
端部力主要由电机端部结构决定,当离开端部距离约为初级长度的2%时,端部力即可忽略不计,因此有文献对其结构优化进行了分析,如增加辅助极、端部弧形处理等[12-13]。
4 结 论
(1)直线电机的推力除了名义推力外,还包括很多的谐波推力,主要包括5部分的成分:其一是由电枢电流谐波和次极磁场谐波共同决定的电流基频的6倍频,即为纹波推力,而且受齿槽效应的影响,纹波推力减小为原来的a0(<1)倍;其二是由于齿槽结构决定的以齿距为周期的一系列谐波,即为旋转电机中所熟知的齿槽力;其三是由永磁体磁场、电枢电流以及齿槽效应等共同决定的耦合推力谐波;其四是由于直线电机所特有的端部效应造成的以极距为周期的一系列谐波;其五是由于电机两端开端,绕组电感不对称引起的推力谐波以及由于初级电感饱和与畸变引起的推力谐波。
(2)虽然经过了相应的结构优化与伺服调节,电机推力谐波成分幅值很小,但是考虑到直线电机进给系统的零传动结构,众多的推力谐波成分直接作用于驱动部件,依然会造成不可忽略的位移波动。尤其考虑实际数控机床整体机械特性时,一旦推力谐波成分某一分量频率接近机械系统的固有频率,引起系统共振,会严重恶化进给系统的运动平稳性。
(3)纹波推力幅值随着驱动电流谐波幅值的减小而减小,频率并不发生变化。电机的τ/τs、ws/τs对于齿槽力的主要谐波阶次以及幅值有重要的影响,尤其当ws/τs=0.625时,齿槽力各阶次谐波均为0。
[1] PRITSCHOW G, PHILIPP W. Direct drives for high-dynamic machine tool axes [J]. CIRP Annals: Manufacturing Technology, 1990, 39(7): 413-416.
[2] 卢秉恒, 赵万华, 张俊, 等. 高速高加速度下的进给系统机电耦合 [J]. 机械工程学报, 2013, 49(6): 2-11. LU Bingheng, ZHAO Wanhua, ZHANG Jun, et al. Electromechanical coupling in the feed system with high speed and high acceleration [J]. Journal of Mechanical Engineering, 2013, 49(6): 2-11.
[3] LIU Hui, YANG Xiaojun, ZHANG Huijie, et al. Research on mechatronic coupling facts of linear motor feed drive system based on spectrum characteristics [C]∥ASME International Mechanical Engineering Congress and Exposition.Houston,Texas,USA: ASME, 2012: 895-903.
[4] ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors: part 1 Open-circuit field [J]. IEEE Transactions on Magnetics, 1993, 29(1): 124-135.
[5] LIU Ruozhu, YANG Qingdong, TONG Liang. Thrust ripples test and analysis of permanent magnet linear synchronous motor [C]∥International Conference on Measuring Technology and Mechatronics Automation. Piscataway, NJ, USA: IEEE, 2011: 1017-1022.
[6] REMY G, GOMAND J, BARRE P J, et al. New current control loop with resonant controllers by using the causal ordering graph-application to machine tools [J]. WSEAS Transactions on Systems, 2006, 5(1): 233-239.
[7] TAN K K, ZHAO S. Adaptive force ripple suppression in iron-core permanent magnet linear motors [C]∥IEEE International Symposium on Intelligent Control. Piscataway, NJ, USA: IEEE, 2002: 266-269.
[8] ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors: part 3 Effect of stator slotting [J]. IEEE Transactions on Magnetics, 1993, 29(1): 143-151.
[9] ZARKO D, BAN D, LIPO T A. Analytical calculation of magnetic field distribution in the slotted air gap of asurface permanent-magnet motor using complex relative air-gap permeance [J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828-1837.
[10]MARKOVIC M, JUFER M, PERRIARD Y. Reducing the cogging torque in brushless DC motors by using conformal mappings [J]. IEEE Transactions on Magnetics, 2004, 40(2): 451-455.
[11]JIAN Linni, CHAU K T, GONG Yu, et al. Analytical calculation of magnetic field in surface-inset permanent magnet motors [J]. IEEE Transactions on Magnetics, 2009, 45(10): 4688-4691.
[12]CHUNG S, LEE H, HWANG S. A novel design of linear synchronous motor using FRM topology [J]. IEEE Transactions on Magnetics, 2008, 44(6): 1514-1517.
[13]YANG Tong, ZHOU Libing, LI Langru. Influence of design parameters on end effect in long primary double-sided linear induction motor [J]. IEEE Transactions on Plasma Science, 2011, 39(1): 192-197.
[14]ZHU Y, LEE S, CHUNG K, et al. Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM [J]. IEEE Transactions on Magnetics, 2009, 45(6): 2863-2866.
[15]HIRASA T, ISHIKAWA S, YAMAMURO T. Equivalent circuit of linear induction motors with end effect taken into account [J]. Electrical Engineering in Japan, 1980, 100(2): 65-71.
[16]GIERAS J F, DAWSON G E, EASTHAM A R. A new longitudinal end effect factor for linear induction motors [J]. IEEE Transactions on Energy Conversion, 1987, 2(1): 152-159.
[17]张颖. 永磁同步直线电机磁阻力分析及控制策略研究 [D]. 武汉: 华中科技大学, 2008.
[18]马志云. 电机瞬态分析 [M]. 北京: 中国电力出版社, 1998: 43-48.
[19]刘成颖, 沈祥明, 王昊. 永磁直线同步电机非线性电感与推力波动的分析和补偿 [J]. 清华大学学报, 2010, 50(12): 1968-1973. LIU Chengying, SHEN Xiangming, WANG Hao. Analysis and compensation of the nonlinear inductance and thrust ripple in permanent magnet linear synchronous machine [J]. Journal of Tsinghua University, 2010, 50(12): 1968-1973.
(编辑 杜秀杰)
Spectrum Characteristics of Thrust in Linear Motor Oriented to Motion Stability
MA Chengfang1,2,YANG Xiaojun1,2,ZHANG Jun1,2,LÜ Dun1,2,ZHAO Wanhua1,2
(1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China)
Harmonic force of linear motor acts directly on the drive element, which reduces the motion stability of the feed system. The servo drive circuit and the nonlinear of motor structure are considering. With the equivalent magnetizing current method and Maxwell equations, the analytic expression of ripple force, cogging force, end effect force, coupling force and inductance asymmetry force are obtained. In the computation process, the coupling effect between multiple harmonic factor is considered, which makes up for the former single factor analysis of harmonic force. The results show that the thrust in the linear motor contains multiple harmonic force, influenced by the servo drive circuit and the nonlinear of motor structure, and each harmonic component gets mutually coupled. These harmonic force acts directly on the mechanical system to lead to the displacement wave of feed system. The effect of the harmonic force rises with the increasing speed. Near the speed of 5, 20 and 33 m/min, the harmonic force results in system resonance to seriously weaken motion stability of the feed system. The amplitude of ripple force declines with the decreasing amplitude of the harmonic current. The ratio between pole pitch and tooth space pitch and ratio between tooth space opening and pitch exert an important influence on the harmonic frequency and amplitude of cogging force, especially, the cogging force disappears in the ratio of tooth space opening and pitch of 0.625.
linear motor; harmonic force; motion stability; system resonance
2015-01-27。 作者简介:马成方(1990—),男,硕士生;赵万华(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金重点资助项目(51235009)。
时间:2015-05-04
10.7652/xjtuxb201508008
TH113.2
A
0253-987X(2015)08-0045-07
网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150504.0900.006.html

