采用信息理论准则的信号源数估计方法及性能对比
成玮,张周锁,
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
采用信息理论准则的信号源数估计方法及性能对比
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
为了从机械系统观测混合信号中有效评估信号源的数目,以及解决数据点较大时贝叶斯信息准则(BIC)难以计算的问题,在剖析了3种信源数目估计准则(赤池信息准则(AIC)、最小描述长度(MDL)以及贝叶斯信息准则(BIC))的原理和算法的基础上,提出了基于对数函数修正的改进贝叶斯准则(IBIC)。该准则利用对数运算将BIC目标函数中的多参数指数运算转换为乘积运算,在不降低计算精度的条件下,显著改善了BIC准则的计算效率和工程应用性能。仿真实验分析表明:AIC与MDL具有近似的源数估计性能,对非线性调制成分非常敏感;从能量角度分析,提出的新准则容忍非线性调制成分(非线性调制信号能量占观测信号总能量)能量比为5.15%,较AIC(0.07%)与MDL(0.08%)具有更好的鲁棒性能。壳体结构试验台声源数目估计实验表明,3种方法均可有效评估声源数目。本研究对于模态阶数选择、系统复杂度分析以及基于机械系统信号源分离的状态监测与故障诊断具有学术意义和工程应用价值。
源数估计;信息理论准则;赤池信息准则;最小描述长度;贝叶斯信息准则
在大多数物理系统中,观测信号可以建模为有限个信源和噪声的线性叠加。基于线性叠加理论的主分量分析[1]、盲源分离[2-3]、独立分量分析技术[4-6]由于可有效分析这类物理系统而获得广泛的工程应用。信源有效分离的首要条件是精确估计信源数目。当前的信源数目估计方法在处理机械系统时由于结构传递特性以及信源混合方式而受到限制,本文将探讨基于信息理论准则的信源数目估计方法处理机械系统信号时的性能。
近十年来,国内外许多学者通过改进现有信源数目估计方法和提出新的理论方法解决源数估计问题。如文献[7]提出了多源干扰下的声源数目和方位估计方法并给出了实验验证;文献[8]提出了基于独立分量分析的信源数目估计方法并将其应用于机械系统中;文献[9]提出了一种基于线性阵列和嵌套数组的信源数目估计方法。然而,现有文献中对信源数目估计理论方法研究较多,但应用源数估计方法解决机械系统工程问题的研究文献很少。信源数目估计是有效分析系统信号组成成分以及复杂程度的关键,因此研究机械系统源数估计方法对于机械系统复杂程度分析以及振动噪声溯源具有重要的工程价值。
与基于特征值分解通过设定噪声子空间门限实现信源数目估计方法不同,基于信息理论的源数估计方法通过目标函数极值特性自适应估计信源数目,如赤池信息准则[10]、最小描述长度[11]、贝叶斯信息准则[12]等。然而,基于贝叶斯信息准则的源数估计方法计算复杂,并且存在当数据点数较大时难以计算的技术难题。针对上述问题,本文提出了一种改进的贝叶斯准则(IBIC),在不降低计算精度的条件下提高了计算效率,具有更好的工程应用性能。本研究通过数值仿真和实验定量比较了上述方法应用于机械系统的性能,可用于模态参数选择、系统复杂性分析、以及机械信号源盲分离,研究结论对于机械系统故障诊断与振动噪声溯源具有重要的学术意义和工程价值。
1 源数估计理论
1.1 信源线性叠加模型
对于包含n个信号源S(t)=[s1(t),…,sn(t)]T的m个不同位置观测获取的混合信号X(t)=[x1(t),…,xm(t)]T,假定每个观测混合信号分别是所有源信号与噪声信号N(t)=[n1(t),n2(t),…,nm(t)]通过混合矩阵A={aij}m×n的线性叠加,于是观测混合信号X(t)可以描述如下


(1)
假定R=E[XXT](E表示期望函数)是观测混合信号X(t)的自相关矩阵,特征值满足λ1≥λ2≥…≥λm,L(n)是一个对数似然函数,表达式如下

(2)
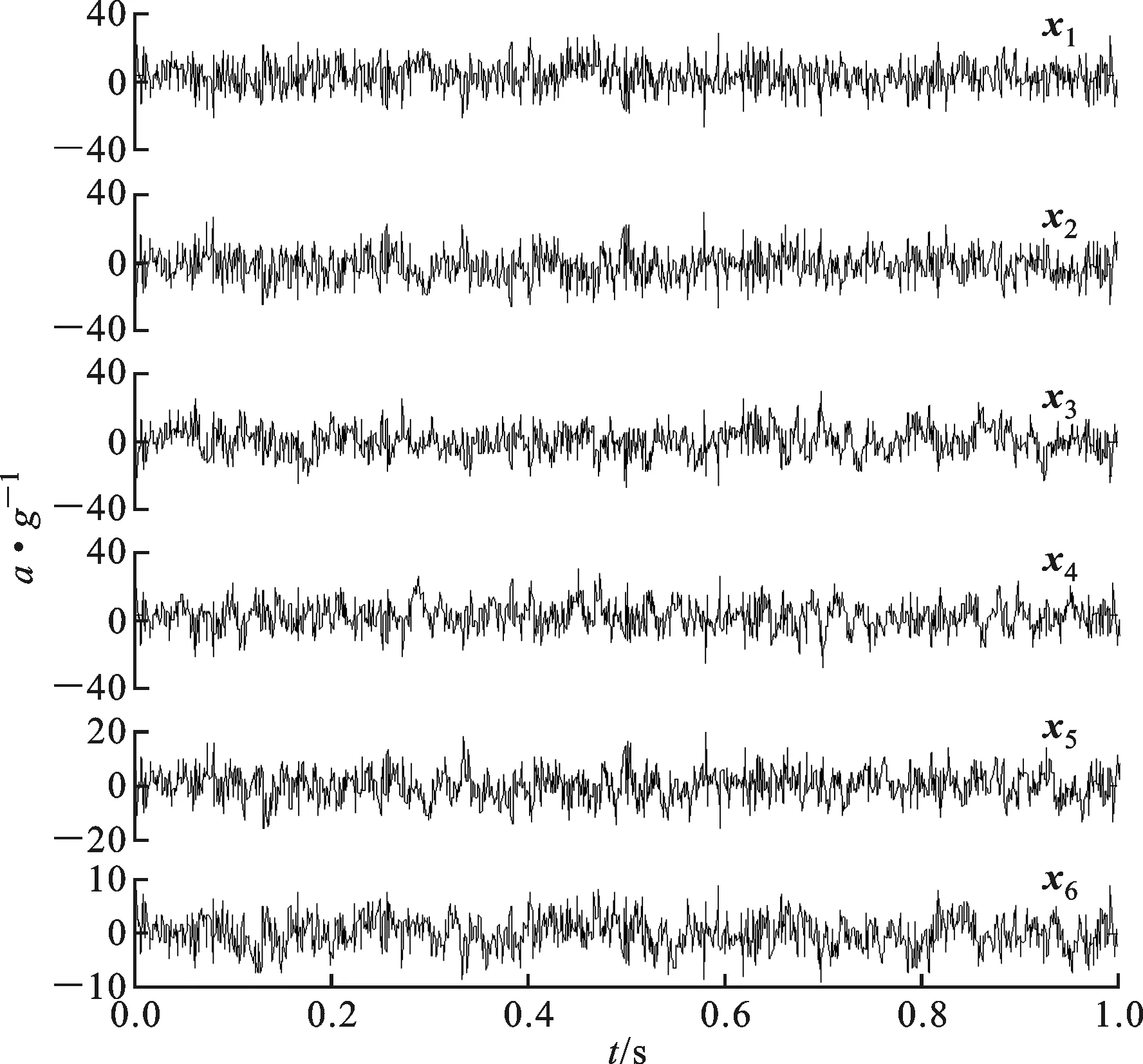
基于线性叠加理论的信号处理方法如主分量分析等的中心问题是选择需要保留的分离分量个数,将m维信号投影到n(n 1.2 赤池信息准则(AIC) 基于赤池信息理论准则的源数估计方法通过最小化目标函数AIC,实现模态阶数或者源数n*的自适应判定,AIC计算原理如下 (3) 式中:N为数据长度。 AIC函数由两部分构成,第一项体现了主分量对参数拟合的好坏,随着阶数(信源数目)的增加而变小;第二项表示主分量n的多少,随着阶数的增加而变大。当两者之和取最小值意味着权衡了两方面的因素,进而获得信源数目的次最佳估计。 1.3 最小描述长度(MDL) 基于最小描述长度准则的源数估计方法是通过最小化目标函数MDL实现源数n*的自适应判定,MDL计算原理如下 (4) 对比MDL与AIC目标函数可以看出,MDL采用了与AIC相近的信息理论准则,只是在两者权重方面做了参数修正,本质上都是对主分量数目与拟合性能的全面考虑。 1.4 贝叶斯信息准则(BIC) 基于贝叶斯信息理论准则的源数估计方法是通过最大化目标函数BIC实现源数n*的自适应判定,BIC计算原理如下 BIC(n)=p(X|n)≈ (5) 式中 (6) (7) Minka的实验表明,BIC相对于源信号的概率分布十分稳健,对数据点数较少的时候也表现出稳健性[14]。但是,BIC或IBIC在使用中应该考虑两个前提条件: (1)混合信号数目m必须大于源信号数目n; (2)观测信号中应该混有少量的噪声。 2.1 源信号和观测信号 给定源信号s1(t)是一个正弦信号,模拟机械系统的简谐振动;s2(t)是一个频率调制信号,模拟机械系统的频率调制特性;s3(t)是一个幅值调制信号,模拟机械系统的幅值调制特性;s4(t)是一个白噪声信号,模拟机械结构噪声与环境噪声。仿真实验源信号的波形如图1所示,其中a为加速度,g为重力加速度。 图1 源信号波形图 混合信号通过源信号以线性叠加与非线性调制混合产生,非线性混合因子σ用于定量反映各种方法对非线性成分的容忍性能,其中线性混合系数为随机产生,非线性混合因子σ人为设定。混合信号生成函数见式(8),其波形如图2所示。 图2 观测信号波形图(σ=0.097 4) (8) 从图1可以看出,源信号1、2、3波形具有典型的特征信息:源信号1是典型的正弦函数,源信号2具有明显频率调制特征,源信号3具有明显的幅值调制特征,源信号4是白噪声,波形非常复杂。图2中所有观测信号波形复杂,几乎不能直接从观测混合信号中识别出源信号波形特征信息。 2.2 信源数目估计方法性能分析 通过调整非线性混合因子σ可定量获得非线性混合成分的鲁棒性能,仿真实验从σ=0.000 1开始逐步增加,AIC、MDL与IBIC 3种方法分别在σ=0.001 3、σ=0.001 5以及σ=0.097 4时失效,3种方法计算准确率如图3所示。图3表明,AIC与MDL性能非常接近,MDL较AIC鲁棒性能稍优,IBIC较AIC与MDL具有更好的非线性调制成分鲁棒性能,对于处理机械系统中广泛存在的调制现象工程意义显著。 图3 基于信息理论准则方法的准确率比较 2.3 信源数目估计 AIC在σ=0.001 3、MDL在σ=0.001 5以及IBIC在σ=0.097 4条件下的估计结果如图4所示。从图中可以看出:当σ增至0.001 3时,AIC在n=5时获得最小值-0.097 4;当σ增至0.001 5时,MDL在n=5时获得最小值-0.070 8;当σ增至0.097 4时,IBIC在n=1时获得最大值-0.893 5。换言之,AIC、MDL与IBIC分别在不同的非线性成分影响下失效,这进一步说明了机械系统调制成分对基于线性叠加理论的信源数目估计方法性能的严重影响,同样也定量验证了3种方法对非线性调制成分的鲁棒性能。 图4 不同参数条件下的源数估计结果 综上分析,在包含弱非线性调制成分的仿真实验中,AIC与MDL取得近似的源数估计性能,两者对非线性调制成分的鲁棒性差,比较而言MDL较AIC略优。从能量角度分析,IBIC容忍非线性调制成分的能量比(噪声能量占观测信号总能量)为5.15%(观测信号x6(t)非线性成分能量比为E[σs1s3]/(E[0.43s1]+E[0.27s2]+E[0.14s3]+E[0.32s4]+E[σs1s3])=5.15%,其中E为能量),IBIC较AIC(能量比为0.07%)与MDL(能量比为0.08%)具有更为显著的鲁棒性,较适合于处理壳体机械系统中信源数目估计。实际工程应用中必须提前考虑非线性混合成分能量比例。 3.1 实验台简介 为了定量比较基于信息理论准则的信源数目估计方法处理机械系统的性能,搭建了壳体结构实验台。实验台基本结构与实物图分别如图5a和5b所示。实验中,通过距离壳体0.5m的不同方位传感器阵列获取观测信号,实验参数如表1所示,源信号与观测信号波形分别如图6和图7所示。 表1 实验参数列表 从图6中可以看出:源信号1和源信号2具有典型的周期特征,喇叭波形信息与理论波形特征信息非常接近,具有典型正弦波形特征;源信号3波形信息较为复杂,具有周期性成分与幅值调制成分混合叠加的特征。相比源信号波形,图7中所有观测信号波形较为复杂,难以直接从观测混合信息中评估出准确的信源数目和波形信息。图8表明,虽然所有观测信号均含有不同幅值的840、1 600、3 000 Hz频率成分,但是由于观测信号为各个源信号的复杂混合,不能直接从观测信号中辨识出独立源信号的主要组成成分。此外,许多工程应用中信源真实波形信息是难以直接获取,因此信源数目估计不仅提供系统复杂程度的精确认识,降低了问题维数(难度),而且对盲源分离提供了准确源数,可显著提高其信源分离能力。 a:端盖; b:喇叭I; c:左支撑肋; d:喇叭II; e:壳体;f:电机; g:右支撑肋; h:橡胶弹簧; i:支架 (a)基本结构 (b)实物图图5 壳体结构实验台 图6 源信号波形图 图7 观测信号波形图 图8 观测信号频谱图 3.2 源数估计 基于信息理论准则的信源数目估计方法分析机械系统声学信号,结果如图9所示。从图9中可以明显看出:随着信源数目的增加,AIC与MDL变化趋势近似,在n*=4时目标函数分别取得极小值-0.980 6和-0.817 1;IBIC变化较小,在n*=4时目标函数取得极大值1.000。从基于信息理论准则的定义可知,3种基于信息理论准则的信源数目估计方法认为6组观测混合信号中包含有4个信源,这与实验台3个机械噪声源不符。考虑到实验设置及环境噪声的影响,研究中将利用独立分量分析方法进行信号分离,提取分离分量并定量分析观测信号中包含的源信息成分,进而对基于信息理论准则的信源数目估计方法提供可靠的实验验证。 图9 基于信息理论准则的信源数目估计结果 3.3 有效性验证 为了验证基于信息理论准则的信源数目估计方法处理机械噪声信息的有效性,利用独立分量分析方法,将6组观测信号在信源数目为4的初始条件下进行了独立分量分离,所提取的独立分量波形如图10所示。对比图10和图6可以看出,独立分量1与源信号1波形非常近似,具有典型的正弦周期特征;独立分量2与源信号2波形一致,具有清晰的正弦特征信息;独立分量3与源信号3特征近似,都含有周期成分并有明显的幅值调制现象;独立分量4波形复杂,与各个源信号波形具有明显的差异。 图10 盲源分离提取独立分量波形图 波形信息特征分析仅能给出定性的判断,研究将利用精确的频谱特征信息对比给出定量说明。源信号和独立分量的频谱分别如图11和图12所示。图11表明:源信号1含有明显的特征频率3 kHz;源信号2含有明显的特征频率1.6 kHz;源信号3的频谱成分主要分布于0.4~1.3 kHz内,并具有显著的特征频率0.84 kHz,上述3个特征频率均包含在图8所示观测信号中。 图11 源信号频谱图 图12 盲源分离提取独立分量频谱图 对比图11与图12可以看出:独立成分1、2、3分别与源信号1、2、3具有相同的特征频率,表明观测信号中包涵了源信号1、2、3的波形特征信息;独立分量4频谱成分复杂,频谱无明显特征信息,能量分布较为广泛,包含了从0~5 kHz频段内成分,特征与白噪声频谱特征类似,分析认为是实验中环境噪声所致。 通过独立分量分析的信源分离,以及分离分量与源信号的波形与频谱特征分析可以看出:6组观测混合信号中包涵了全部3个源信号,并且在实验过程中额外含有了环境噪声信息,致使信源数目从3变成4,因此实验分析认为真实信源数目为4。这与基于信息理论准则的信源数目估计方法得到的结论一致,进而验证了基于信息理论准则的信源数目估计方法在处理机械噪声信息中的有效性。 信号源数目估计是准确分析系统复杂程度的前提条件,也是盲信号处理的关键技术。本文剖析了3种基于信息理论准则的信源数目估计方法及其计算原理,并改进了基于贝叶斯信息理论准则的信源数目估计方法,显著提高了其计算效率和工程应用性能。仿真分析表明,AIC与MDL具有近似的信源数目估计性能,两者对线性叠加系统有效,但对非线性调制成分非常敏感,IBIC较AIC与MDL对非线性混合特征具有更好的鲁棒性能,对于机械系统具有较好的工程应用价值。壳体结构实验台声源数目估计表明,3种方法均有效估计出了信源数目为4(3个机械噪声源与1个环境噪声源)。借助独立分量分析信源分离、波形定性分析与频谱定量分析,基于信息理论准则的信源数目估计有效性得到了可靠的实验验证。研究为模态阶数选择、系统复杂性分析以及基于机械系统信源分离的状态监测与故障诊断技术提供了重要的先验信息。 [1] WIESEL A, HERO A O. Decomposable principal component analysis [J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4369-4377. [2] COMON P, JUTTEN C. Handbook of blind source separation [M]. Waltham, MA, USA: Academic Press, 2010. [3] CHENG W, ZHANG Z S, LEE S, et al. Investigations of denoising source separation technique and its application to source separation and identification of mechanical vibration signals [J]. Journal of Vibration and Control, 2014, 20(14): 2100-2117. [4] HYVARINEN A. Fast and robust fixed-point algorithm for independent component analysis [J]. IEEE Transactions on Neural Networks, 1999, 10(3): 626-634. [5] HYVARINEN A, OJA E. Independent component analysis: algorithms and applications [J]. Neural Networks, 2000, 13(4/5): 411-430. [6] CHENG W, ZHANG Z, LEE S, et al. Source contribution evaluation of mechanical vibration signals via enhanced independent component analysis [J]. Journal of Manufacturing Science and Engineering, 2012, 134(2): 160-165. [7] HU J S, YANG C H. Estimation of sound source number and directions under a multisource reverberant environment [J/OL]. EURASIP Journal on Advanced in Signal Processing, 2010: 870756 [2014-11-20]. http:∥asp.eurasipjournals.com/content/2010/1/870756. [8] CHENG W, LEE S, ZHANG Z S, et al. Independent component analysis based source number estimation and its comparison for mechanical systems [J]. Journal of Sound and Vibration, 2012, 331(23): 5153-5167. [9] HAN KY, NEHORAI A. Improved source number detection and direction estimation with nested arrays and ULAS using JACKKNIFING [J]. IEEE Transactions on Signal Processing. 2013, 61(23): 6118-6128. [10]WILLIANMS D B. Counting the degrees of freedom when using AIC and MDL to detect signals [J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3282-3284. [11]HUANG L, SO H C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix [J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4806-4821. [12]DING Q, KAY S. Inconsistency of the MDL: on the performance of model order selection criteria with increasing signal-to-noise ratio [J]. IEEE Transactions on Signal Processing, 2011, 59(5): 1959-1969. [13]马建仓, 牛奕龙, 陈海洋. 盲信号处理 [M]. 北京: 国防工业出版社, 2006: 35-65. [14]MINKA T P. Automatic choice of dimensionality for PCA [C]∥14th Annual Neural Information Processing Systems Conference. Cambridge, MA, USA: MIT Press, 2001: 598-604. [本刊相关文献链接] 徐光华,张锋,谢俊,等.稳态视觉诱发电位的脑机接口范式及其信号处理方法研.2015,49(6):1-7.[doi:10.7652/xjtuxb201506001] 熊涛,江桦,崔鹏辉,等.应用基扩展模型的混合信号单通道盲分离算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010] 刘进,李赞,高锐.低信噪比下采用广义随机共振的能量检测算法.2015,49(6):27-32.[doi:10.7652/xjtuxb201506005] 刘进,李赞,高锐.低信噪比下采用广义随机共振的能量检测算法.2015,49(6):27-32.[doi:10.7652/xjtuxb201506005] 郝雯洁,齐春.一种鲁棒的稀疏信号重构算法.2015,49(4):98-103.[doi:10.7652/xjtuxb201504016] 孙锦华,韩会梅.低信噪比下时频联合的载波同步算法.2015,49(2):62-68.[doi:10.7652/xjtuxb201502011] 唐成凯,廉保旺,张玲玲.卫星通信系统双向中继转发自干扰消除算法.2015,49(2):74-79.[doi:10.7652/xjtuxb201502 013] 王静,黄建国,侯云山.采用峰值平均功率比的低信噪比水下多目标检测方法.2012,46(2):124-129.[doi:10.7652/xjtuxb201202021] 蔡改改,陈雪峰,陈保家,等.利用设备响应状态信息的运行可靠性评估.2012,46(1):108-113.[doi:10.7652/xjtuxb 201201020] 国强,王常虹,李峥.支持向量聚类联合类型熵识别的雷达信号分选方法.2010,44(8):63-67.[doi:10.7652/xjtuxb201008 013] 鲁慧民,冯博琴,李旭.面向多源知识融合的扩展主题图相似性算法.2010,44(2):20-24.[doi:10.7652/xjtuxb201002005] 种稚萌,朱世华,吕刚明.分布式Alamouti空时码的信道容量分析.2007,41(8):969-973.[doi:10.7652/xjtuxb200708 020] (编辑 杜秀杰) Information Criterion-Based Source Number Estimation Methods with Comparison (State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China) To effectively evaluate the source number of mechanical systems from the measured mixed signals, and solve the calculating difficulty of BIC for large data points, three information criterion-based source number estimation methods, Akaike information criterion (AIC), minimum description length (MDL), and Bayesian information criterion (BIC), are comparatively studied and an improved BIC, named IBIC, is proposed following an exponential function modification, which transforms the multi-parameter exponential calculating to multiplications. Without decreasing the accuracy, IBIC obviously improves the calculating efficiency and engineering application performances. The numerical case study results show that AIC and MDL obtain the similar performances on source number estimation, and they are both very sensitive to the nonlinear modulation effects. In respect to signal energy ratios, the proposed method has a robustness tolerance on nonlinear modulation effects for 5.15%, which is higher than that of AIC (0.07%) and MDL (0.08%). The results of source number estimation for acoustical signals of a test bed with shell structures show that all the three methods are effective for the given acoustical signals. This work benefits model order selection, complexity analysis of a system, and applications of source separation to mechanical systems for the condition monitoring and fault diagnosis purposes. source number estimation; information criteria; Akaike information criterion; minimum description length; Bayesian information criterion 2014-12-12。 作者简介:成玮(1983—),男,讲师。 基金项目:国家自然科学基金资助项目(51305329);教育部高等学校博士学科点专项科研基金资助项目(20130201120040);中国博士后科学基金资助项目(2013M532032,2014T70911)。 时间:2015-05-04 10.7652/xjtuxb201508007 TH17 A 0253-987X(2015)08-0038-07 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150504.0900.004.html

2 仿真分析



3 实验研究










4 结 论


