采用空间极化时频分布的跳频信号多参数联合估计算法
张东伟,郭英,2,齐子森,张坤峰,张波,侯文林
(1.空军工程大学信息与导航学院,710077,西安;2.通信网信息传输与分发技术重点实验室,050081,石家庄)
采用空间极化时频分布的跳频信号多参数联合估计算法
张东伟1,郭英1,2,齐子森1,张坤峰1,张波1,侯文林1
(1.空军工程大学信息与导航学院,710077,西安;2.通信网信息传输与分发技术重点实验室,050081,石家庄)
为了在欠定条件下利用信号二维波达方向(2D-DOA)与极化状态进行跳频(FH)网台分选和信号识别、跟踪,提出了一种基于空间极化时频分布(SPTFD)的FH信号多参数联合估计算法。首先利用FH信号时频域特征以及阵列流型建模方法,建立FH信号的极化敏感阵列快拍数据模型;然后通过组合时频分布构造各跳信号的SPTFD矩阵;在此基础上,根据秩损理论对方向和极化信息进行去耦合,利用旋转不变子空间原理估计俯仰角;通过一维搜索和方程求解来估计方位角与极化参数,最终实现了2D-DOA与极化参数的联合估计。新算法无需多维参数寻优和配对,估计精度高。仿真结果表明:该算法能在欠定条件下精确估计FH信号2D-DOA和极化参数;当阵元数为4、信噪比大于6 dB时,空间5个FH信号所有参数的均方根误差均小于1°。
跳频;极化;时频分布;参数估计
跳频(FH)通信因其优越的抗干扰、抗截获和多址组网等能力,已逐渐成为军事通信的主导技术[1]。信号波达方向(DOA)和极化状态在FH网台分选、信号属性识别、跟踪和干扰等诸多任务中具有重要作用[2-8]。文献[2-4]提出了基于空时数学模型的FH信号DOA估计方法,但要求信源数已知且小于阵元数,不能用于欠定情况;文献[5-7]基于空时频处理思想,通过构造FH信号各跳的时频域协方差矩阵,利用子空间原理估计一维DOA,但未考虑2D-DOA问题,无法定位三维空间目标。
作为电磁波的重要属性,极化增加了信息处理维度,结合信源方位能够显著提高FH信号辨识度[6]。同时,极化信息的引入有利于提高阵列系统的DOA估计精度[9]。然而,目前关于FH信号DOA和极化联合估计的研究成果非常少见,可查资料中,仅文献[8]有所涉及,但最多仅能处理5个信号,限制了该算法的应用范围。因此,亟待寻求FH信号DOA和极化状态的有效估计方法。此外,实际系统中阵元数受限,而空间信源数未知,特别是战时FH组网密度高,易出现欠定情况。综上所述,对于FH侦察,在欠定条件下开展2D-DOA和极化参数的联合估计具有重要理论价值和现实意义,但关于该问题的研究鲜有报道。
本文通过引入空间极化时频分布和秩损理论解决FH信号多参数联合估计问题。首先建立FH信号的极化敏感阵列快拍数据模型,同时采用一种新的组合时频分布方法抑制FH交叉项以得到清晰稳健的时频图,进而选取各跳自项时频点构造其空间极化时频分布(SPTFD)矩阵;在此基础上,通过阵列流形形式变换结合秩损理论将方向和极化信息进行去耦合,利用最小二乘ESPRIT原理估计俯仰角;通过一维角度搜索和方程求解估计方位角与极化参数,最终实现了FH信号2D-DOA与极化参数的联合估计。本文算法能用于欠定情况,且无需高维参数寻优和配对,在保证估计精度的前提下有效减小了计算复杂度。
1 FH信号的阵列快拍数据模型
设FH信号s(t)的跳周期为T,在观测时间内共包含K跳,第k(k=1,…,K)跳的载频为ωk,起始跳的持续时长为Δt0,则s(t)可表示为[1]

(1)
式中:t′=t-(k-1)T-Δt0;v(t)是s(t)的基带复包络;φk是第k跳的初相;rect(t)为单位矩形窗。在空间直角坐标系中分别沿X轴和Z轴方向构造用正交电偶极子组成的均匀线阵,记为子阵1、子阵2。子阵1和子阵2的阵元数均为M,阵元间隔分别为d1、d2,并满足max(d1,d2) 图1 L型正交电偶极子阵列结构 假设相位描述子为(γ,η)(γ∈[0,π/2]为极化辅角,η∈[0,2π]为极化相位差)的窄带平面波S以俯仰角θ∈[0,π/2)和方位角φ∈[0,2π)沿单位方向-u入射,则极化矢量为[9] (2) 式中:γy、γz分别表示沿Y轴和Z轴方向的电场分量。假设阵列单元增益为1并忽略单阵元共点接收通道不一致及互耦影响,子阵1的导向矢量为 (3) 式中:p=e-(j2πd1sinθcosφ)/λ为相邻阵元的相位差,λ=c/f(c为光速,f为载频)为该跳信号波长;M为阵元数;运算符⊗为Kronecker积。同理,子阵2的导向矢量为 (4) 式中:q=e-(j2πd2cosθ)/λ。因此,阵列导向矢量为 (5) 当空间存在N个信源s1~sN时,阵列流型矩阵为 (6) 阵列的快拍数据矩阵为 (7) 式中:S(t)为信源的N×1维数据矢量;N(t)为阵列的4M×1维噪声数据矢量。 构造FH信号各跳的SPTFD矩阵是讨论多参数联合估计算法的基础。下面首先简述SPTFD的基本原理,然后采取一种有效抑制交叉项的时频分析方法得到清晰时频图以确定各跳自项区(用自项时频点构造SPTFD矩阵是算法性能正常发挥的前提),同时设计SPTFD矩阵的高效构造策略。推导中假设噪声为零均值且与信号不相关。 2.1 SPTFD的基本原理[10] SPTFD指将时频分布扩展至极化敏感阵列信号,其突出优势是可实现信号的选择性估计,同时增加了极化域处理维度,利于提高DOA估计精度和获取信源极化信息。对于信号x1(t)和x2(t),离散时间形式的Cohen类互时频分布为 (8) 式中:φ(l,τ)为核函数。SPTFD矩阵定义为 (9) (10) E[DXX(t,f)]与单极性阵列时域协方差模型Rxx=E[x(t)xH(t)]=ARssA+σ2IM具有类似结构,且与A有相同的子空间特性。为确保E[DXX(t,f)]满秩,通常选择关注信号的多个自项时频点采取联合对角化或平均处理对其进行估计。 2.2 组合时频分布及SPTFD矩阵构造策略 Wigner-Ville分布(WVD)的时频聚焦性能最佳,但对多分量信号存在严重交叉项干扰且抗噪性能一般。平滑伪Wigner-Ville分布(SPWVD)经过时、频域2次平滑,在交叉项抑制、时频聚焦性和抗噪能力这3个方面都取得了很好平衡。本文将WVD和SPWVD进行组合,使两者的优势均得以保留用于FH信号分析。SPWVD&WVD组合时频分布的基本思想是:首先将SPWVD和WVD结果进行点乘得到模具矩阵以抑制绝大部分交叉项;再对模具矩阵进行截断处理进一步抑制噪声,得到自项时频地图;最后将自项时频地图与SPWVD结果进行点乘得到组合时频分布。将参考阵元Z轴方向接收通道的SPWVD和WVD结果分别记为TSPWVD(t,f)和TWVD(t,f),自项时频地图记为MAU(t,f),有 (11) 式中:运算符⊙表示Hadamard积;ξ为截断门限,ξ=μmean{|TSPWVD(t,f)⊙TWVD(t,f)|},其中μ为门限因子,mean{·}代表取均值。 图2为3个FH信号的时频分布结果。可见,组合时频分布沿袭了WVD的时频聚焦性,交叉项和噪声也消除殆尽。由于组合时频分布确定的自项区域包含于SPWVD结果。因此,构造SPTFD矩阵时,组合时频分布仅需作用于参考阵元以提供各跳信号时频点选取范围。为降低计算量,式(9)中Cohen分布可采用与SPWVD性能近似,计算量却大为降低的SPW分布[6]。 (a)WVD (b)SPWVD (c)SPWVD&WVD组合图2 多FH信号的3种时频分布结果(RSN=5 dB) 3.1 信源方位和极化参数去耦合 对FH信号任意一跳,设其对应的信源数为L,根据式(9)构造SPTFD矩阵E{DXX(t,f)}|in并对其进行特征分解得到噪声子空间UN,根据子空间原理并考虑噪声和有限快拍数影响,定义以下优化问题估计信源参数 (12) (13) 式中:F(θ,φ)只包含由波程差导致的相位差;Y只包含极化参数。根据秩损理论[11],当且仅当(θ,φ)为真实方位时,式(14)成立 (14) 由于Y不全为0,可通过二维搜索得到成对的俯仰角和方位角 (15) 式中:χmin[·]为求矩阵最小特征值算子。 3.2 俯仰角和方位角估计 根据式(15)估计方向角仍需二维搜索,下面寻找满足旋转不变关系的成对子阵,根据最小二乘ESPRIT原理对俯仰角进行独立估计,从而避开二维搜索,进一步降低运算量。设Aq1和Aq2分别为由A的第2M+1,2M+3,…,4M-1行和第2M+2,2M+4,…,4M行元素组成的子阵,则有 (16) (17) 式中:Yk,k=1,2,…,L为各信源对应的极化矢量;qk=e-(j2πd2cosθk)/λin,k=1,2,…,L;Φq=diag[q1,q2,…,qL]。由式(16)和(17)可见,Aq1和Aq2满足旋转不变关系,求得Φq对角元素即可解得俯仰角。假设E{DXX(t,f)}|in的信号子空间和噪声子空间分别为Us、Un,由于span{Us}=span{A},按照由A构成Aq1和Aq2的方式将Us划分成2个分块矩阵Us1和Us2,存在唯一的非奇异矩阵T满足 (18) span(Aq1)=span(Us1)=span(Aq2)=span(Us2) (19) 所以,Us2=Us1T-1ΦqT=Us1Ψq,可见矩阵Ψq的特征值即为Φq对角元素qk,则俯仰角估计值为 (20) Ψq利用最小二乘ESPRIT算法[12]求得 (21) 将式(20)俯仰角估计值作为已知参数代入式(15),得方位角估计值 (22) 3.3 极化参数估计 (23) 式中:emin[·]表示求矩阵最小特征值对应的特征矢量算子。结合式(2),得极化比为 (24) 因此极化参数估计值为 (25) 式中 (26) 通过方位角、俯仰角与极化参数之间的解析关系式(13)、式(22)和式(23)可知,经过上述处理过程,各参量实现了自动配对。 3.4 性能分析 (1)只要各信号在时-频域上存在差异,就可分别构造其SPTFD矩阵,通过该算法估计各信号参数,从而使阵列所能处理的FH信号总数不受阵元数限制。选取自项时频点构造SPTFD矩阵等价于进行时频域滤波,显著提高了目标信号信噪比,因此本文算法具有较强的信噪比适应能力。 (2)俯仰角直接利用最小二乘ESPRRIT算法得到,影响估计精度的因素主要为噪声;方位角基于俯仰角估计值,由一维角度搜索得到,误差来源还包括俯仰角估计误差和角度搜索步长;极化角则受俯仰角和方位角估计误差的双重影响。因此,同等条件下,俯仰角的估计性能最优,方位角次之,极化参数最差。 (3)阵元数增加时,阵列孔径增大;各跳信号的快拍数增加时,构造SPTFD矩阵可供利用的有效时频点更多,有利于更充分的利用时频信息和保证SPTFD矩阵的列满秩;因此,算法性能随着阵元数和快拍数的增加而提高。当发生频率碰撞时(对应跳为多源估计问题),由于信号间互扰的存在,导致算法估计性能差于无碰撞时。 3.5 本文算法步骤 根据以上推导和阐述,可得FH信号2D-DOA和极化参数联合估计算法步骤如下: (1)对参考阵元数据进行组合时频分布,估计各跳持续时间、载频和跳时刻[13],确定自项区; (2)根据式(9)、(10)构造某跳信号的SPTFD矩阵E[DXX(t,f)]|in,并对其进行特征值分解; (3)估计该跳对应的信源数L; (7)返回步骤(2)直至完成所有跳估计。 阵列结构如图1所示,2个子阵的阵元间距均为1.5 m;5个远场FH信号(FH1~FH5)参数分别为[20°,30°,40°,45°]、[30°,40°,50°,60°]、[40°,50°,60°,75°]、[50°,60°,75°,45°]、[60°,70°,35°,45°];角度搜索步长0.05°;STFT平滑窗的采样点数为335,SPWVD时域平滑窗的采样点数为335,频域平滑窗的采样点数为101;构造SPTFD矩阵时去除各跳首尾100个时频点以避免平滑窗导致的相位模糊;截断因子μ取0.1。均方根误差(RMSE)定义为 (27) 实验1 暂无频率碰撞,空间存在FH1、FH2和FH3,跳周期均为10 μs,采样率100 MHz,采样点数3 000;ULA阵元数M设为4,信噪比从-6 dB以2 dB间隔递增到40 dB,各信噪比下进行100次Monte-Carlo实验。图3和图4分别为(总体)估计成功概率(估计成功概率定义见文献[11])及均方根误差曲线。 图3 实验1的估计成功概率 图4 实验1各参数的均方根误差曲线 实验结果表明,随着信噪比的提高,各参数估计成功概率均逐渐增加:信噪比大于10 dB时,总体估计成功概率逐渐接近100%;俯仰角和方位角的估计成功概率较高,基本保持在90%以上;极化参数性能略差,但当信噪比大于8 dB时也达到90%以上。算法对方位角、俯仰角和极化角的RMSE值均较小,误差水平满足高分辨要求;俯仰角的估计精度最高,方位角次之,极化参数略差。 实验2 为验证阵元数对算法性能的影响,在信噪比分别取0 dB和6 dB时,单臂ULA阵元数从4以2为间隔递增到14,其余条件同实验1。 图5 总体估计成功概率与阵元数的关系 图5和图6为算法性能与阵元数目的关系曲线。从图5可见,阵元数对本文算法性能具有较大影响:随着阵元数增加,总体估计成功概率随之提高(信噪比为6 dB,阵元数大于12时达到100%)。从图6可以看出,各参数RMSE值随阵元数的增加均逐步降低,但相比俯仰角和方位角,极化参数的RMSE曲线下降趋势不明显。 图6 各参数RMSE与阵元数的关系 实验3 为验证快拍数对算法性能的影响,在信噪比分别取0 dB和6 dB时,各跳快拍数从400渐增至2 000,其余条件同实验1(为保证公平,各FH信号均包含3跳进行性能统计平均,因此各跳快拍数的变化体现为跳周期和采样时长的区别)。图7和图8为算法性能与快拍数的关系曲线。 图7 总体估计成功概率与快拍数的关系 图8 均方根误差与快拍数的关系 图7表明,总体估计成功概率随着快拍数增加而提高,即跳周期越长估计性能越好。图8表明,各参数RMSE值随快拍数的增加均逐步降低,但极化参数的RMSE性能差于俯仰角和方位角。 实验4 5个FH信号同时存在,为验证算法在欠定条件和频率碰撞时的性能,设定两信号间发生频率碰撞的概率为1(每次实验随机选择一跳发生碰撞),3个信号以上的碰撞概率为0,其余条件与实验1相同。实验结果如图9、图10所示。 图9 欠定条件和频率碰撞时的估计成功概率 图10 欠定条件和频率碰撞时各参数的RMSE 图9、图10表明:在欠定条件和存在频率碰撞时,估计性能依然良好;信噪比大于14 dB时,总体估计成功概率接近100%;信噪比大于6 dB时所有参数的RMSE均小于1度。频率碰撞时相应跳为多源估计,因此对比图9与图3发现,实验4的估计性能略差于实验1。本文实验设定的碰撞概率条件非常苛刻,已远超实际情况(通常两电台某跳发生频率碰撞已属小概率事件),证明在欠定条件和频率碰撞时本文算法依然有效。 为了有效辅助FH网台分选及信号识别、跟踪,本文提出了基于空间极化时频分布的FH信号二维波达方向与极化参数联合估计算法。通过SPWVD & WVD组合时频分布抑制交叉项和噪声,确保利用自项时频点构造各跳信号的SPTFD矩阵,进而根据秩损和子空间原理实现二维波达方向与极化参数的精确估计。仿真结果表明,在频率碰撞和欠定条件下本文算法取得了优良的参数估计性能,为欠定条件下跳频通信侦察提供了新思路。 [1] FU K C, CHEN Y F. Blind iterative maximum likelihood-based frequency and transition time estimation for frequency hopping systems [J]. IET Communications, 2013, 7(9): 883-892. [2] LIU X Q, NICHOLAS D S, SWAMI A. Blind high-resolution localization and tracking of multiple frequency hopped signals [J]. IEEE Transactions on Signal Processing, 2002, 50(4): 889-901. [3] LIU X Q, NICHOLAS D S, SWAMI A. Joint hop timing and frequency estimation for collision resolution in FH networks [J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 3063-3074. [4] LIN C H, FANG W H. Joint angle and delay estimation in frequency hopping systems [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1042-1056. [5] 陈利虎, 张尔扬. 基于数字信道化和空时频分析的多跳频信号DOA估计 [J]. 通信学报, 2009, 30(10): 68-74. CHEN Lihu, ZHANG Eryang. Directions of arrival estimation for multi frequency-hopping signals based on digital channelized receiver and spatial time-frequency analysis [J]. Journal of Communications, 2009, 30(10): 68-74. [6] 陈利虎. 跳频信号的侦察技术研究 [D]. 长沙: 国防科学技术大学, 2009. [7] 王永明, 王世练, 张尔扬. 多跳频脉冲的高效测向算法 [J]. 哈尔滨工程大学学报, 2011, 32(5): 662-666. WANG Yongming, WANG Shilian, ZHANG Eryang. An effective direction finding method for multi-frequency hopping pulses [J]. Journal of Harbin Engineering University, 2011, 32(5): 662-666. [8] WONG K T. Blind beamforming/geolocation for wide-band FFHs with unknown hop-sequences [J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 65-76. [9] 庄钊文, 徐振海, 肖顺平, 等. 极化敏感阵列信号处理 [M]. 北京: 国防工业出版社, 2005: 199-212. [10]ZHANG Y M, OBEIDAT B A, AMIN M G. Spatial polarimetric time frequency distribution for direction of arrival estimation [J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1327-1340. [11]齐子森, 郭英, 王布宏, 等. 共型阵列天线信源方位与极化状态的联合估计算法 [J]. 电子学报, 2012, 40(12): 2562-2566. QI Zisen, GUO Ying, WANG Buhong, et al. Joint DOA and polarization estimation algorithm for conformal array antenna [J]. Acta Electronica Sinica, 2012, 40(12): 2562-2566. [12]王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法 [M]. 北京: 清华大学出版社, 2004: 185-211. [13]付卫红, 王璐, 贾坤, 等. 基于STFT与SPWVD的跳频参数盲估计算法 [J]. 华中科技大学学报: 自然科学版, 2014, 42(9): 59-63. FU Weihong, WANG Lu, JIA Kun, et al. Blind parameter estimation for frequency hopping signals based on STFT and SPWVD [J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014, 42(9): 59-63. [本刊相关文献链接] 尚佳栋,王祖林,周丽娜,等.采用随机共振增强的混合扩频信号跳频参数估计.2014,48(10):42-48.[doi:10.7652/xjtuxb201410007] 郑纪彬,任爱锋,苏涛,等.多分量Chirp信号相位参数的精确估计算法.2013,47(2):69-74.[doi:10.7652/xjtuxb201302 012] 王云龙,吴瑛.联合时延与多普勒频率的直接定位改进算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020] 熊涛,江桦,崔鹏辉,等.应用基扩展模型的混合信号单通道盲分离算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010] (编辑 刘杨) A Joint Estimation Algorithm of Multiple Parameters for Frequency Hopping Signals Using Spatial Polarimetric Time Frequency Distributions ZHANG Dongwei1,GUO Ying1,2,QI Zisen1,ZHANG Kunfeng1,ZHANG Bo1,HOU Wenlin1 (1. School of Information and Navigation, Air Force Engineering University, Xi’an 710077, China; 2. Science and Technology on Information Transmission and Dissemination in Communication Networks Laboratory, Shijiazhuang 050081, China) A novel multi-parameter joint estimation algorithm based on spatial polarimetric time-frequency distributions (SPTFD) for frequency-hopping (FH) signals is proposed to sort frequency-hopping network, identifying and to track signals effectively via the two dimensional direction of arrival (2D-DOA) and polarization of FH signals in underdetermined conditions. Both the time and the frequency features of FH signals are used to derive a data model for its polarization sensitive array based on the modeling method for manifold matrices of arrays; Then a SPTFD matrix for each hop is generated by the combined time-frequency distribution. The 2D-DOA and the polarization information are then de-coupled in the light of rank reduction theory, and the elevation angle is estimated via ESPRIT algorithm. Both the azimuth and the polarization are estimated through one-dimensional search and equation solution, respectively, and the joint estimation of both the 2D-DOA and the polarization of FH signals is completed. The proposed algorithm has good estimate precision without multi parameters optimization or pair-matching. Simulation results show that the proposed algorithm accurately estimates the 2D-DOA and the polarization of FH signals in underdetermined conditions and that the RMSE of all parameters for five FH signals is less than one degree when there are 4 sensors and the SNR is bigger than 6 dB. frequency hopping; polarization; time-frequency distribution; parameter estimation 2014-11-26。 作者简介:张东伟(1987—),男,博士生;郭英(通信作者),女,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61072148);通信网信息传输与分发技术重点实验室基金资助项目(ITD-U12003/K1260009)。 时间:2015-05-15 10.7652/xjtuxb201508004 TN911.7 A 0253-987X(2015)08-0017-07 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150515.1747.003.html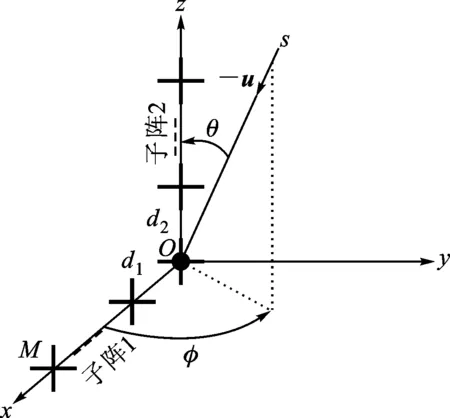

2 FH信号的SPTFD矩阵构造
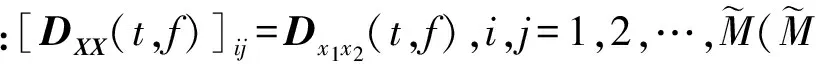

3 2D-DOA与极化参数联合估计




4 仿真结果与分析



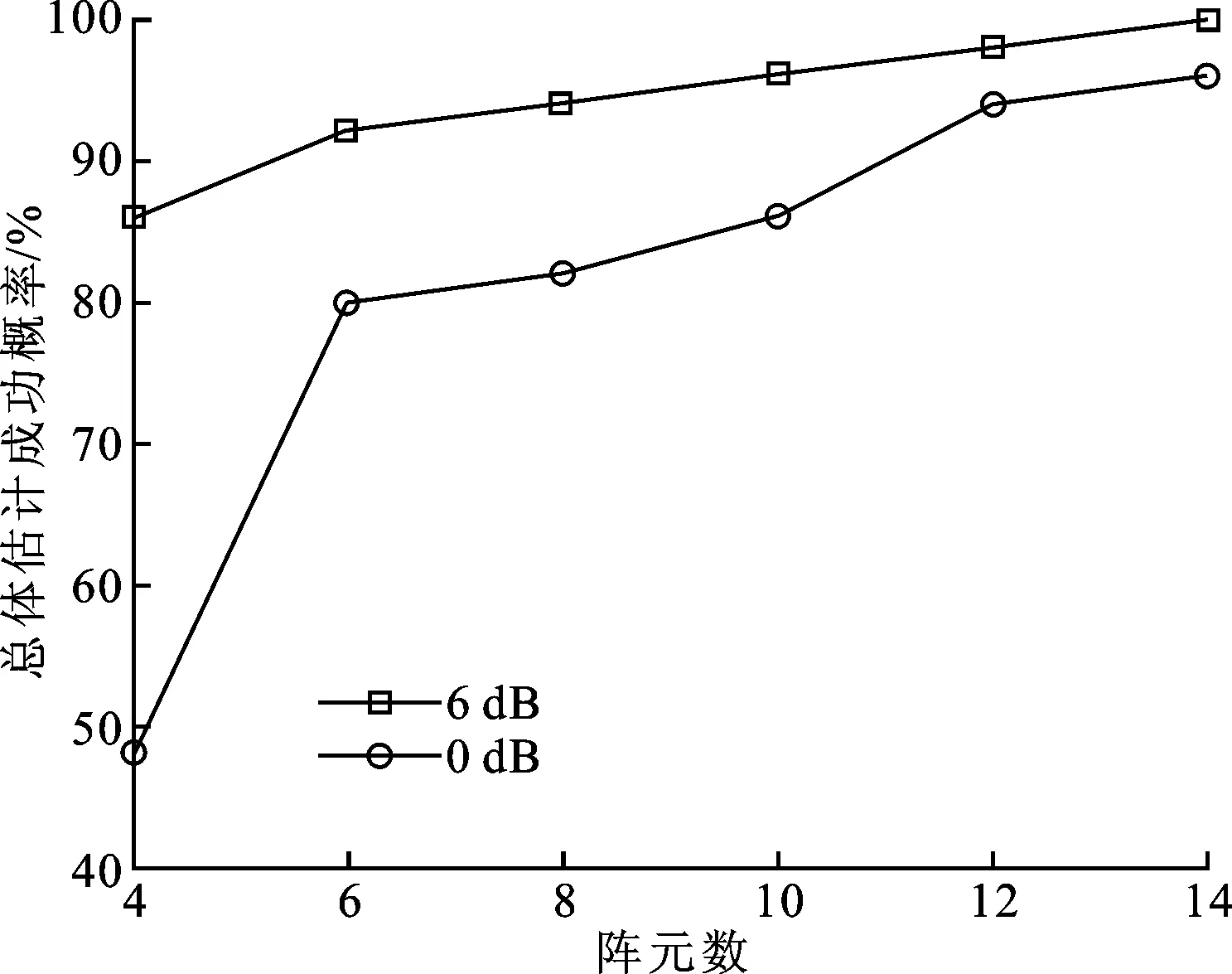





5 结 论

