纤维多孔金属的流阻率分形模型研究
陈卫华,陈天宁,王小鹏,张超
(1.西安交通大学机械工程学院,710049,西安;2.兰州理工大学机电工程学院,730050,兰州)
纤维多孔金属的流阻率分形模型研究
陈卫华1,2,陈天宁1,王小鹏1,张超1
(1.西安交通大学机械工程学院,710049,西安;2.兰州理工大学机电工程学院,730050,兰州)
为了揭示纤维多孔金属吸声材料的流阻率与其孔隙率、孔直径以及孔的弯曲度等主要几何参数之间的变化规律,给纤维多孔金属吸声材料的结构设计提供基本的理论指导,提出了一种流阻率分形模型。通过对纤维多孔金属的孔隙结构进行分形处理,结合材料内部空气流体学分析,首先获得了流经纤维多孔金属材料截面总的空气流量Q的表达式,该表达式是最大平均孔径λmax、曲线分形维数DT和孔面积分形维数Df的函数,其次结合纤维多孔金属吸声材料流阻率的公式,获得了流阻率分形模型。模型理论计算值与实验测试值的最大偏差为13.9%,最小偏差为7.6%,平均偏差为10.6%,验证了该理论模型的可靠性。分析结果表明:随着孔隙率Φ的增大,纤维多孔金属吸声材料的流阻率减小;Φ和DT一定时,流阻率随着Df的增大而减小;Φ和Df一定时,流阻率随着DT的增大而增大。与通过实验确定流阻率的经验公式相比,文中所建流阻率分形模型能够反映材料的几何参数与流阻率之间的变化规律,为纤维多孔金属吸声材料的微观结构设计提供了一定的依据。
流阻率;分形模型;曲线分形维数;孔面积分形维数
烧结纤维多孔金属具有多功能复合特性,例如超轻、高强韧、耐撞击、高比强度、高比刚度、高效散热或隔热以及吸声性能优良等[1],其结构通常由金属骨架和内部介质(通常为空气)组成,金属骨架由一定数量的金属丝按层交错排列高温烧结形成,内部具有复杂的开孔或闭孔结构。与传统的非金属吸声材料相比,纤维多孔金属材料能够耐高温高压,因此可以用作极端恶劣工况下的吸声降噪材料。
声波在纤维多孔金属介质中的传播主要考虑两个方面:一是孔隙填充介质中波的传播;二是多孔介质骨架内的弹性波传播。本文假设金属骨架为刚性体,只考虑声波在孔隙空气中的传播。Allard等将纤维材料作为等效流体研究,指出流阻是反映多孔材料吸声性能的一个重要参数[2];Delany等的研究表明,声波在多孔介质中的传播和衰减主要由孔隙中空气的流阻决定,通过空气流阻就能预测多孔介质的吸声性能[3]。Bies等对多孔金属纤维材料的流阻进行了测量,获得了相关实验结果[4]。上述文献研究工作表明,纤维多孔金属的流阻率是决定其吸声性能优劣的一个重要声学参数。
纤维多孔金属介质的内部孔隙结构呈现无规则排列,孔的分布是杂乱无章的无序结构,使得纤维多孔金属吸声材料的设计难度很大。分形几何学以非规则的几何形态为研究对象,可以处理自然界和非线性系统中不光滑的具有自相似性且没有特征长度的形状和现象。因此,本文以分形几何理论为基础,对纤维多孔金属材料的微观孔隙结构进行描述,建立材料的流阻率与分形维数之间的声学模型。
1 分形理论简介
分形几何学产生于20世纪70年代末80年代初,是一门以非规则几何形态为研究对象的新兴学科[5]。分形的概念是由美国学者Mandelbrot于1975年首先提出来的。在自然界中,大量的研究对象例如粗糙表面、海岸线、山脉以及岛屿等,都是无序和不规则的,它们不能用欧式几何进行准确描述,这些对象被称为分形,它们的维数不再是整数而是分数,称为分形维数。这些分形对象满足下式[6]
M(L)~LDf
(1)
式中:M可以是线的长度、平面面积、立方体体积或物体质量;L是测量尺度;Df是分形维数。式(1)表示分形对象的局部和整体具有精确的自相似性。然而,自然界具有精确自相似性的物体几乎没有,绝大部分研究对象都是统计自相似,因此本文中提到的分形维数均是指统计分形维数。
2 纤维多孔金属的分形研究
纤维多孔金属材料内部孔隙结构随着纤维直径、长度以及纤维的相对排列方式而异,实际烧结而成的纤维多孔金属,其纤维的形状与堆积均是无序的。图1为纤维多孔金属的宏观和微观结构图。

(a)宏观结构 (b)截面微观结构图1 纤维多孔金属
纤维多孔金属内部具有不同尺寸的孔,可以看作由一簇具有不同截面积的弯曲毛细管组成,假设毛细管的直径为λ,沿着声波传播方向的长度为Lt(λ),参照毛细管长度为L0,则根据Wheatcraft等的研究[7]可知,纤维多孔金属内部毛细管的直径和长度满足如下分形关系
Lt(λ)=λ1-DTL0DT
(2)
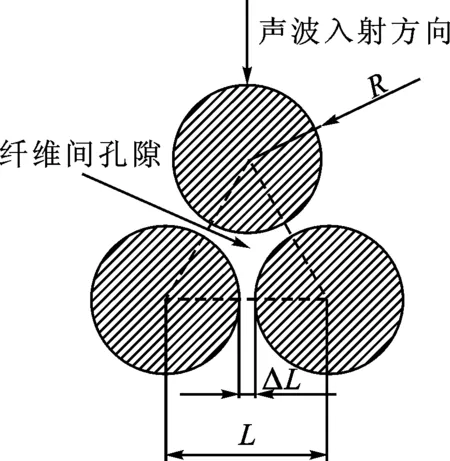
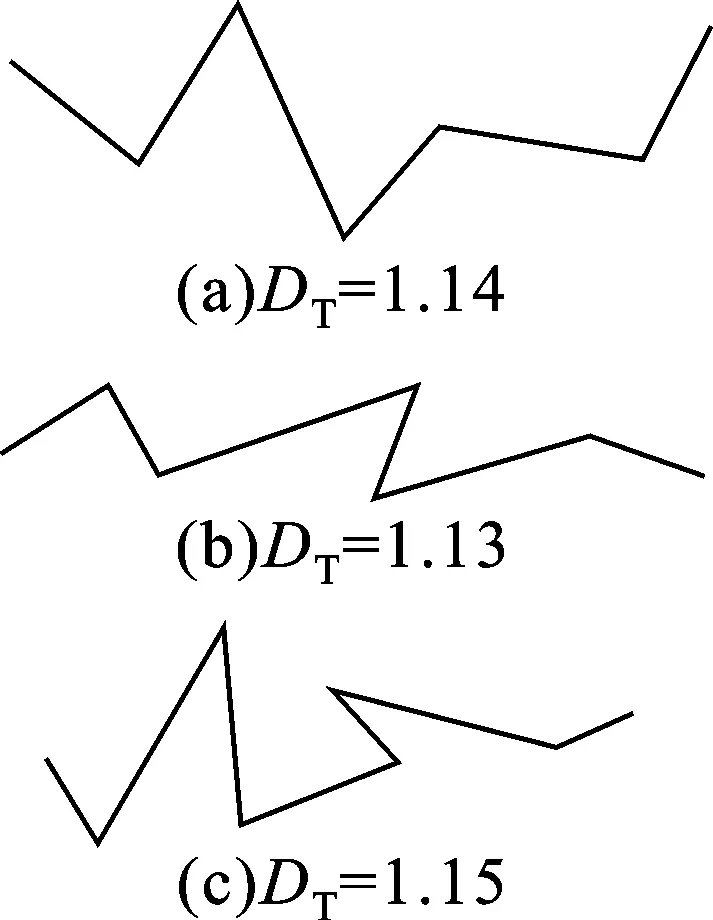
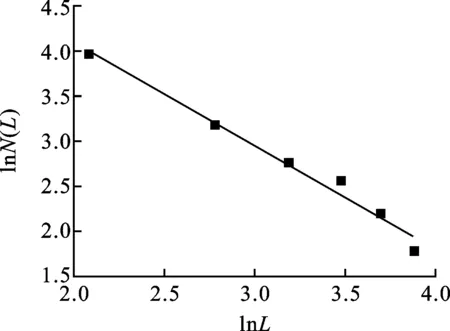
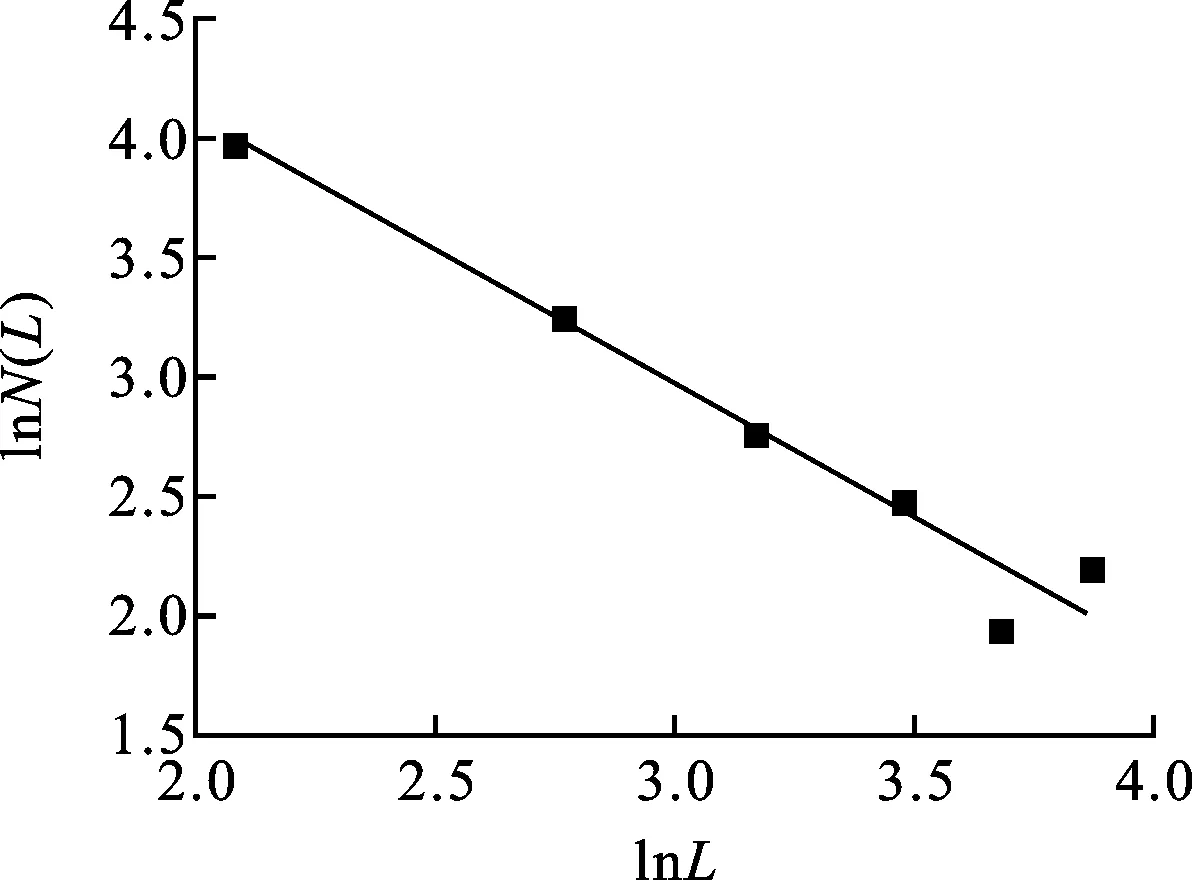
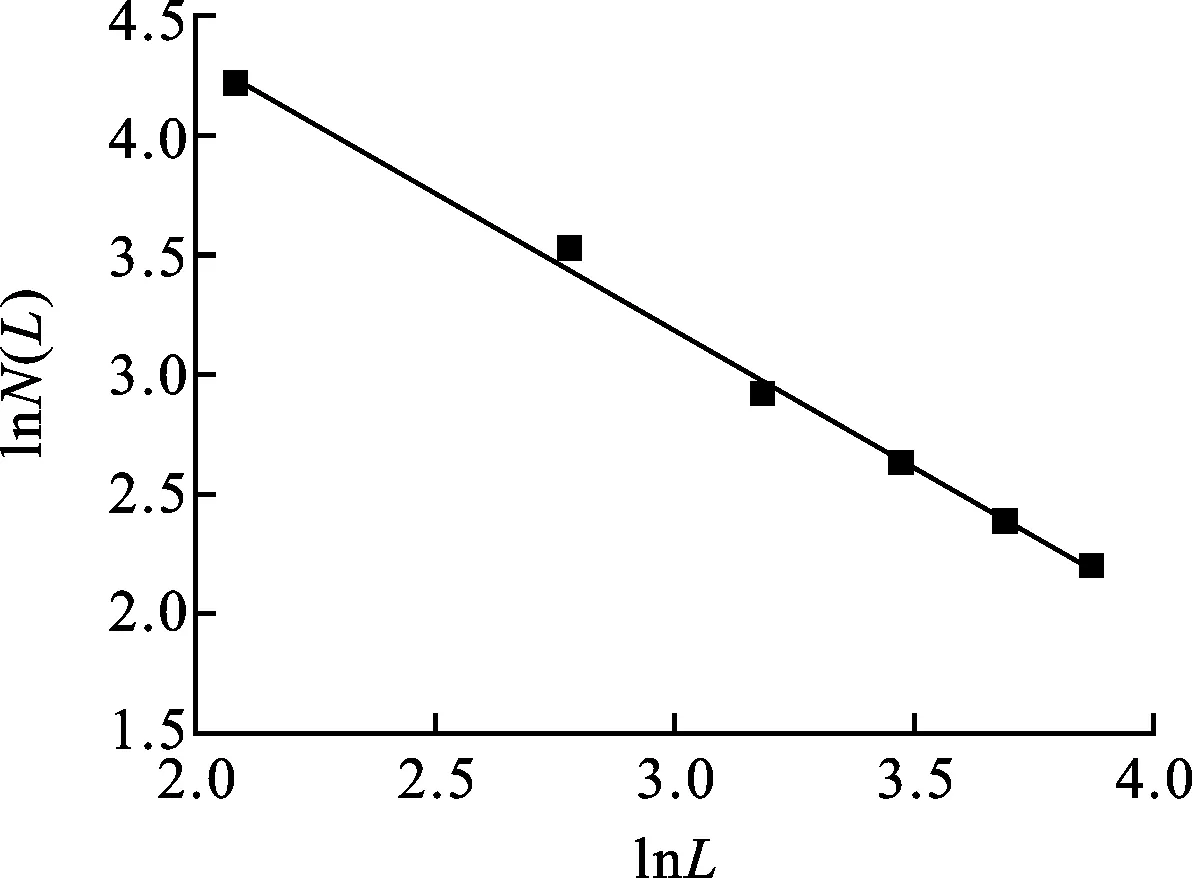
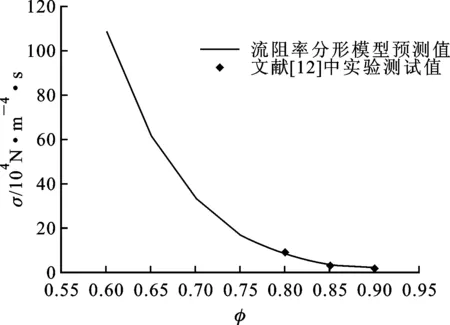
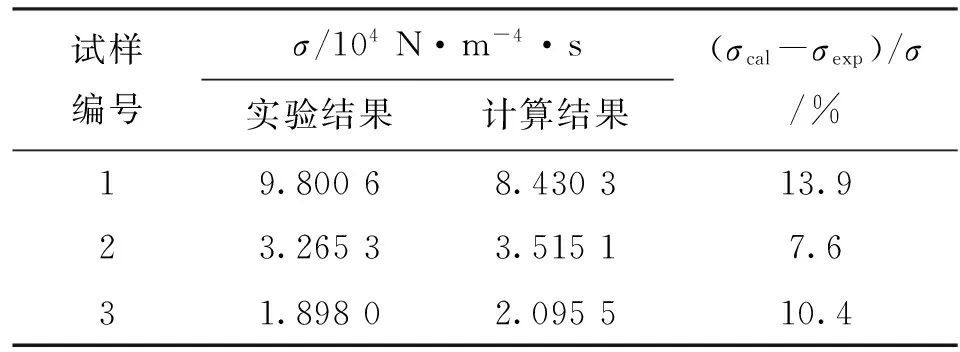
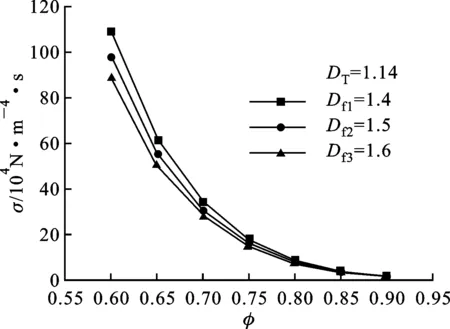
式中:Lt(λ)为毛细管的长度;λ为毛细管的直径;L0为参照毛细管长度;DT为曲线分形维数,1 对于纤维多孔金属材料内部结构来说,除了毛细管的弯曲特性以外,孔直径大于λ的毛细管通道的数量也是一个重要参数。考虑垂直于声波传播方向的一个横截面上分布着直径从λmin到λmax的大小不一的孔,则直径大于λ的毛细管通道数量可以表示为[8] N(L≥λ)=(λmax/λ)Df (3) 式中:N为毛细管通道数量;λmax为毛细管的最大直径。考虑从λ到λ+dλ这一段孔的分布,孔的数量为 -dN=DfλmaxDfλ-(Df+1)dλ (4) 式中:Df为孔面积分形维数。式(4)中负号表示毛细管通道的数量与孔的直径成反比关系。 3.1 空气流量 声波通过纤维多孔金属材料传播时,受到流阻率、声压以及空气的黏性系数等影响,而流阻率与纤维多孔金属的几何结构即孔隙率、毛细管通道的曲线分形维数以及孔面积分形维数相关。下面将首先推导流经材料横截面的空气流量表达式,然后根据达西定律[9]来推导纤维多孔金属的流阻率分形模型。 流经纤维多孔材料空气的总流量为所有毛细管通道空气流量的总和,因此首先考虑单根毛细管通道的空气流量,根据Hagen-Poiseulle方程[10],流经单根毛细管通道的空气流量表达式为 (5) 式中:μ为空气黏性系数;ΔP为声压差;gq为孔形状因子。 总的空气流量Q可以通过对截面孔直径从λmin到λmax范围内的流量进行积分获得[11],联立式(2)、(4)和(5),可得 (6) 式中:1 (7) 上式即为声波入射纤维多孔金属时空气流经纤维多孔介质的总流量表达式。 3.2 流阻率分形模型 根据达西定律,单位时间内流体流经多孔介质的总流量为 (8) (9) 将式(7)、(8)代入(9),可得 (10) 通常情况下,为了便于计算,我们取L0=l,因此式(10)又可以写为 (11) 从式(11)中可以看出,流阻率σ为分形维数DT、Df以及材料结构参数A、L0和λmax的函数。假设毛细管通道是直的,即DT=1,则式(11)又可以写成 (12) 上式表明当声波通过直的纤维多孔金属毛细管通道时,流阻率是孔面积分形维数Df和孔的最大直径λmax的函数,并且跟孔的最大尺寸的4次方成反比。 4.1 纤维多孔金属最大平均孔径λmax的计算 纤维多孔金属材料可以看作由纤维束组成,而纤维束由纤维丝聚集形成,入射声波在纤维束之间的孔隙传播,如图2所示。本文利用三角形孔隙近似表征纤维多孔金属内部的微观孔隙结构,纤维束呈三角形排列形成孔隙,取一个三角形结构单元进行分析。 图2 纤维束间孔隙示意图 对于图2中所示三角形结构单元,孔隙率为 Φ=(A′-πR2/2)/A′ (13) 式中:A′为三角形单元总面积;R为纤维束的半径。A′的表达式为 A′=πR2/[2(1-Φ)] (14) (15) (16) 式中:dmax为孔隙最大直径。将式(16)代入式(15),得到最大孔隙直径dmax的表达式为 dmax=R[2Φ/(1-Φ)]1/2 (17) 式中:Φ为三角形结构单元的孔隙率。声波在实际入射时,不仅要穿过纤维束之间的中心孔隙,而且还要穿过两个相邻的纤维束之间的狭缝,则孔隙最大平均直径还要考虑狭缝的大小,ΔL的表达式为 ΔL=R[(2π)1/23-1/4(1-Φ)-1/2-2] (18) 同时考虑纤维束之间的中心孔隙和相邻两个纤维束之间的狭缝,则单元结构孔隙的最大平均直径λmax近似表示为[11] λmax=(dmax+ΔL)/2 (19) 4.2 分形维数DT和Df 下面采用盒计数方法来确定分形维数DT和Df的值。 4.2.1 曲线分形维数DT对于纤维多孔金属来说,其内部孔结构非常复杂,声波不能沿着直线向前传播。因此,计算声波传播的流阻率就需计算声波传播的毛细管通道的曲线分形维数DT。由于纤维多孔金属内部声波传播路径类似于各向异性介质中的弯曲流道[7],其分形维数可以利用盒计数法来进行计算。图3所示为纤维多孔金属介质中任意3条声波传播路径,假定声波从左向右传播。 利用分形软件FractalFox采用盒计数法分别对图3中3条声波预传播路径曲线分形维数DT进行计算,结果如图4所示。 图3 声波在纤维多孔金属内的预传播路径 4.2.2 孔面积分形维数Df对于纤维多孔金属孔面积分形维数的计算,本文同样采取盒计数法利用分形软件FractalFox进行计算。首先取纤维多孔金属垂直于声波入射方向的一个微小截面,然后利用电子扫描显微镜获得该截面的微观结构图,接着选取边长为L的盒子计算不同L值覆盖截面的盒子个数N(L),再以lnL为横坐标,lnN(L)为纵坐标描出点(lnL,lnN(L)),最后由这些数据点的拟合线的斜率便可以估算出孔面积分形维数Df。 (a)DT=1.14 (b)DT=1.13 (c)DT=1.15图4 3条声波预传播路径的曲线分形维数DT 下面分别对纤维多孔金属的3种试样进行孔面积分形维数Df的计算,表1为试样参数。 表1 纤维多孔金属试样参数 图5为3种试样的微观结构图,放大倍数为100倍。针对3种试样,取盒计数法中盒子尺寸为3~70 mm,步长为10 mm,取自然对数,计算结果如图6所示。 (a)试样1 (b)试样2 (c)试样3图5 纤维多孔金属的微观结构 (a)Df=1.43 (b)Df=1.50 (c)Df=1.54图6 3种纤维多孔金属试样的孔面积分形维数Df 图7 流阻率随孔隙率的变化 为了验证本文流阻率分形模型的可靠性,分别将3种试样的模型预测结果与文献[12]中流阻率实验测试值进行了对比,相关参数为:空气黏性系数μ为1.8×10-5Pa·s(18 ℃);样品长度L0为2.5×10-2m;曲线分形维数DT为1.14;孔面积分形维数Df为1.4;纤维束半径R为3.6×10-4m;试样1、试样2和试样3的孔形状因子gq取为1.11。图7给出了孔隙率分别为80%、85%和90%的3种纤维多孔金属试验样品的流阻率随孔隙率的变化曲线。表2中σcal为流阻率计算值,σexp为流阻率测试值,由表2可见,3种样品流阻率的相对偏差分别为13.9%、7.6%和10.4%,理论计算结果与实验结果吻合得比较好。但是,本文流阻率分形模型是以三角形孔隙近似表征纤维多孔金属材料内部的微观孔结构,尚存在一定误差,后续研究将进一步考虑对纤维多孔金属材料的真实微观结构进行表征,逐步提高模型的估计精度。 表2 流阻率实验结果和计算结果 为了分析孔隙率Φ、曲线分形维数DT和孔面积分形维数Df对声波在纤维多孔金属中传播时流阻率的影响,分别取DT=1.14以及Df=1.5,计算了流阻率随孔隙率的变化曲线,如图8所示。由图8a可见,声波在纤维多孔金属中传播时,当声波传播的孔通道曲线分形维数DT(DT=1.14)一定时,材料的流阻率随着孔隙率的增大而减小,当孔隙率一定时,流阻率随着孔面积分形维数的增大而减小。这是因为当孔面积分形维数和孔隙率增大时,纤维介质中总的孔隙面积也会增大,因此流阻率减小。在图8b中,当孔面积分形维数Df(Df=1.5)一定时,材料的流阻率随着孔隙率的增大而减小,而孔隙率一定时,流阻率随着曲线分形维数的增大而增大。孔隙率和孔面积分形维数一定,当纤维多孔金属的曲线分形维数增大时,声波在介质中传播的路径更曲折,因此流阻率会增大。 (a)σ随Φ及Df的变化 (b)σ随Φ及DT的变化图8 σ随Φ及分形维数的变化 通过本文所建立的流阻率分形理论模型,可以对纤维多孔金属吸声材料的微观孔隙结构进行设计。根据流阻率与孔隙率的变化关系,可在制备纤维吸声材料试样时通过控制孔隙率的大小来获得相应的流阻率变化范围。另外,通过纤维丝的排列可以获得所要求的纤维束尺寸和孔径,从而得到具体的孔面积分形维数,进而估算出流阻率大小。最后,可以对烧结制备纤维吸声材料时每层纤维的疏密程度进行控制,以得到声波在吸声材料中的传播路径,通过流阻率与曲线分形维数的变化关系可以预估流阻率的大小。在实际应用中,可以根据具体降噪的工况要求,按照上述方法来设计相应的纤维多孔金属吸声材料。 本文基于分形几何理论和流体力学理论对声波在纤维多孔金属介质中传播的流阻率进行了研究,建立了流阻率分形模型。模型理论计算值与实验测试值的最大偏差为13.9%,最小偏差为7.6%,平均偏差为10.6%,验证了理论模型的可靠性。同时,在此模型的基础上对相关参数的影响进行了研究,纤维多孔金属材料流阻率随着孔隙率的增大而减小;材料的孔隙率和曲线分形维数一定时,流阻率随着孔面积分形维数的增大而减小;当孔隙率和孔面积分形维数一定时,流阻率随着曲线分形维数的增大而增大。本文研究工作为纤维多孔金属吸声材料的微观结构设计提供了一定的依据。 [1]卢天健, 何德坪, 陈长青, 等.超轻多孔金属材料的多功能特性及应用 [J].力学进展, 2006, 36(4): 517-535. LU Tianjian, HE Deping, CHEN Changqing, et al.The multi-functionality of ultra-light porous metals and their applications [J].Advances in Mechanics, 2006, 36(4): 517-535. [2]ALLARD J F.Propagation of sound in porous media [M].London, UK: Elsevier Applied Science, 1993: 20-22. [3]DELANY M E, BAZLEY E N.Acoustical properties of fibrous materials [J].Applied Acoustics, 1970, 3(2): 105-116. [4]BIES D A, HANSEN C H.Flow resistance information for acoustical design [J].Applied Acoustics, 1980, 13(5): 357-391. [5]朱华, 姬翠翠.分形理论及其应用 [M].北京: 科学出版社, 2011: 1-8. [6]MANDELBROT B B.The fractal geometry of nature [M].New York, NJ, USA: W.H.Freeman and Company, 1982: 23-57. [7]WHEATCEAFT S W, TYLER S W.An explanation of scale-dependent dispersivity in heterogeneous aquifers using concepts of fractal geometry [J].Water Resource Research, 1988, 24(4): 566-578. [8]MAJUMDAR A, BHUSHAN B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J].Journal of Tribology, 1990, 112(2): 205-216. [9]HAPPEL J, BRENNER H.Low Reynolds number hydrodynamics, mechanics of fluids and transport process [M].Boston, MA, USA: Martinus Nejhoff, 1983: 23-57. [10]DENN M M.Process fluid mechanics [M].Englewood Cliffs, NJ, USA: Prentice-Hall, 1980: 35-37. [11]YU Boming, CHENG Ping.A fractal permeability model for bi-dispersed porous media [J].International Journal of Heat and Mass Transfer, 2002, 45(14): 2983-2993. [12]ZHANG Bo, CHEN Tianning.Calculation of sound absorption characteristics of porous sintered fiber metal [J].Applied Acoustics, 2009, 70(2): 337-346. (编辑 武红江) A Fractal Model of Flow Resistivity for Fibrous Porous Metals CHEN Weihua1,2, CHEN Tianning1, WANG Xiaopeng1, ZHANG Chao1 (1.School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China;2.College of Mechano-Electronic Engineering, Lanzhou University of Technology, Lanzhou 730050, China) A fractal model of flow resistivity is proposed to investigate the relations of flow resistivity with some geometric parameters of fibrous porous metals such as porosity, pore diameter and tortuosity, and to obtain a theoretical guidance for the design of sound-absorption materials.First of all, a mathematical expression of the flowQis obtained based on the theory of fractal geometry and fluid mechanics, and the expression is a function of the maximal mean diameter of poreλmax, the fractal dimensionDTof tortuosity and the pore area fractal dimensionDf.Then, the fractal model of flow resistivity is acquired in terms of the flow resistivity formula.The maximum error, the minimum error and the mean error between experimental results and calculation results from the model are 13.9 %, 7.6 % and 10.6 %, respectively, which verifies the accuracy of the model.The calculation results show that the flow resistivity decreases as the porosityΦincreases.When the porosityΦand the tortuosity fractal dimensionDTare fixed, the flow resistivity decreases as the pore area fractal dimensionDfincreases.However, when the porosityΦand the pore area fractal dimensionDfare fixed, the flow resistivity increases as the tortuosity fractal dimensionDTincreases.The relations between the flow resistivity and the geometric parameters are revealed more clearly by the fractal flow resistivity model than by the empirical model.It can be concluded that the results provide a reliable and theoretical guidance for the design of sound-absorption materials. flow resistivity; fractal model; tortuosity fractal dimension; pore area fractal dimension 2014-11-23。 作者简介:陈卫华(1976—),男,在职博士生,兰州理工大学讲师;王小鹏(通信作者),男,副教授。 基金项目:国家重点基础研究发展规划资助项目(2011CB610306);陕西省自然科学基金资助项目(2015JM5154)。 时间:2015-03-23 http:∥www.cnki.net/kcms/detail/61.1069.T.20150323.1713.001.html 10.7652/xjtuxb201506021 TB535 A 0253-987X(2015)06-0132-063 纤维多孔金属的流阻率模型
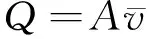
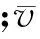
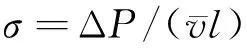
4 流阻率相关参数的计算
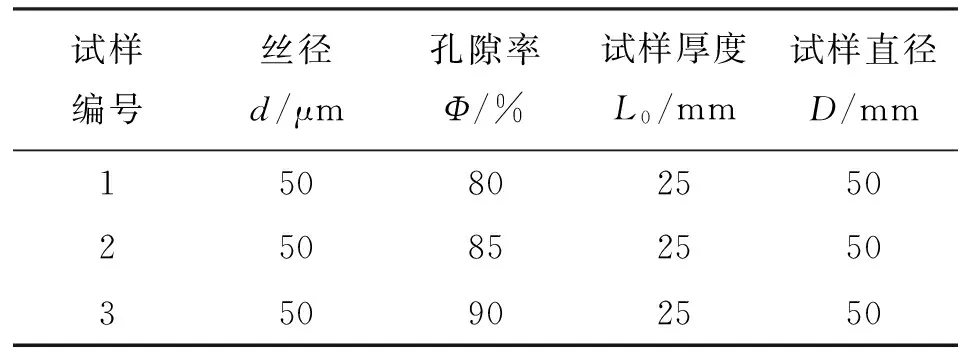


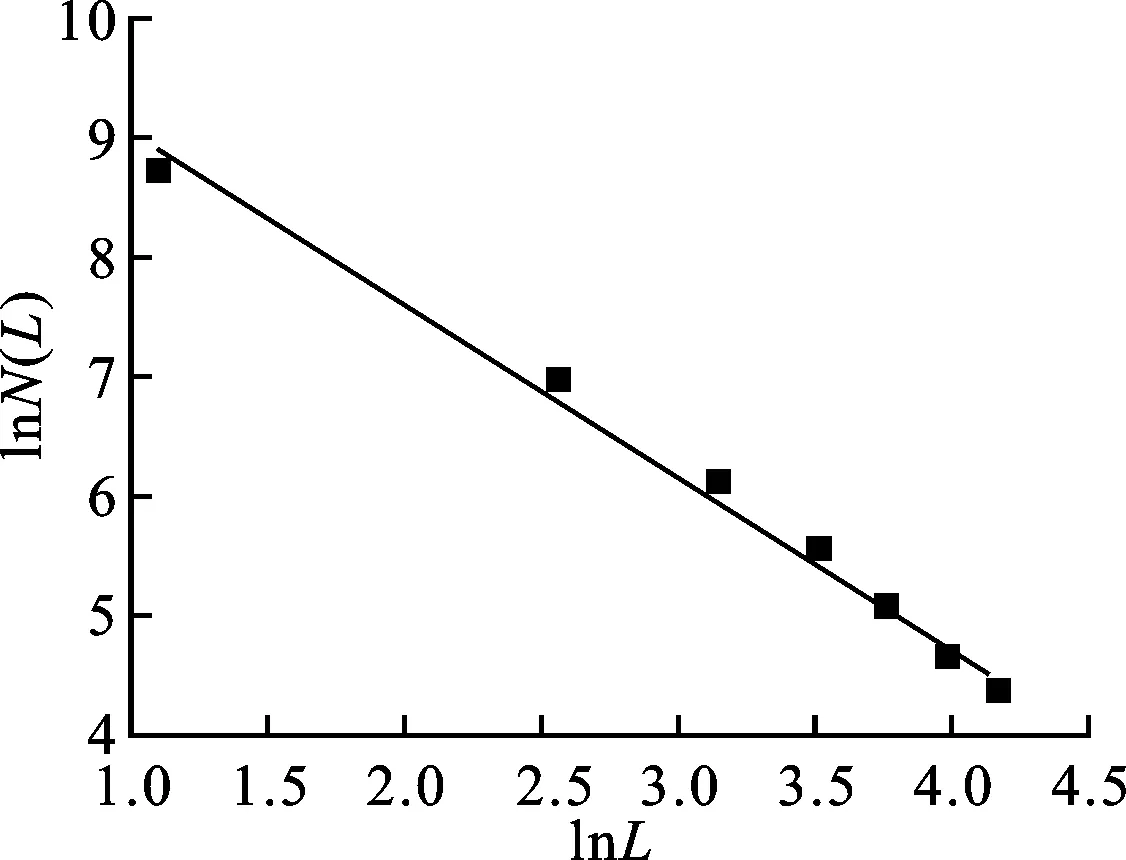
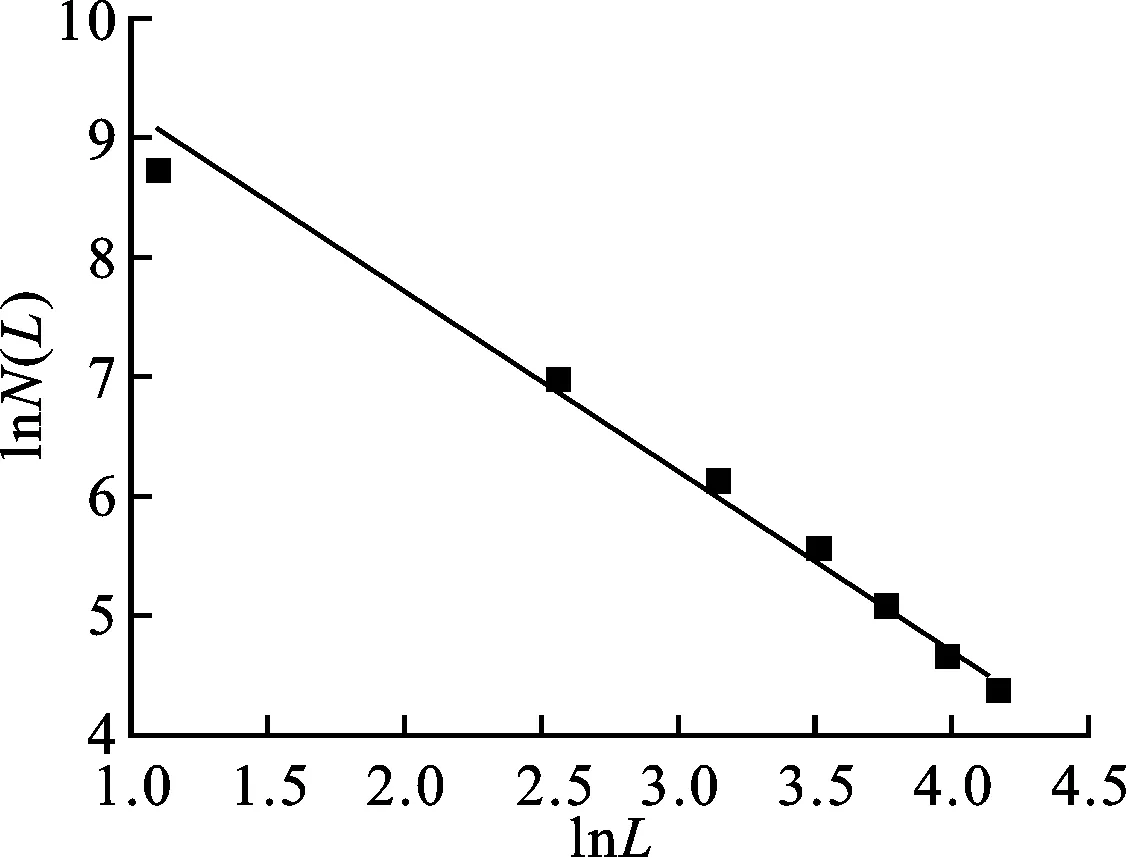
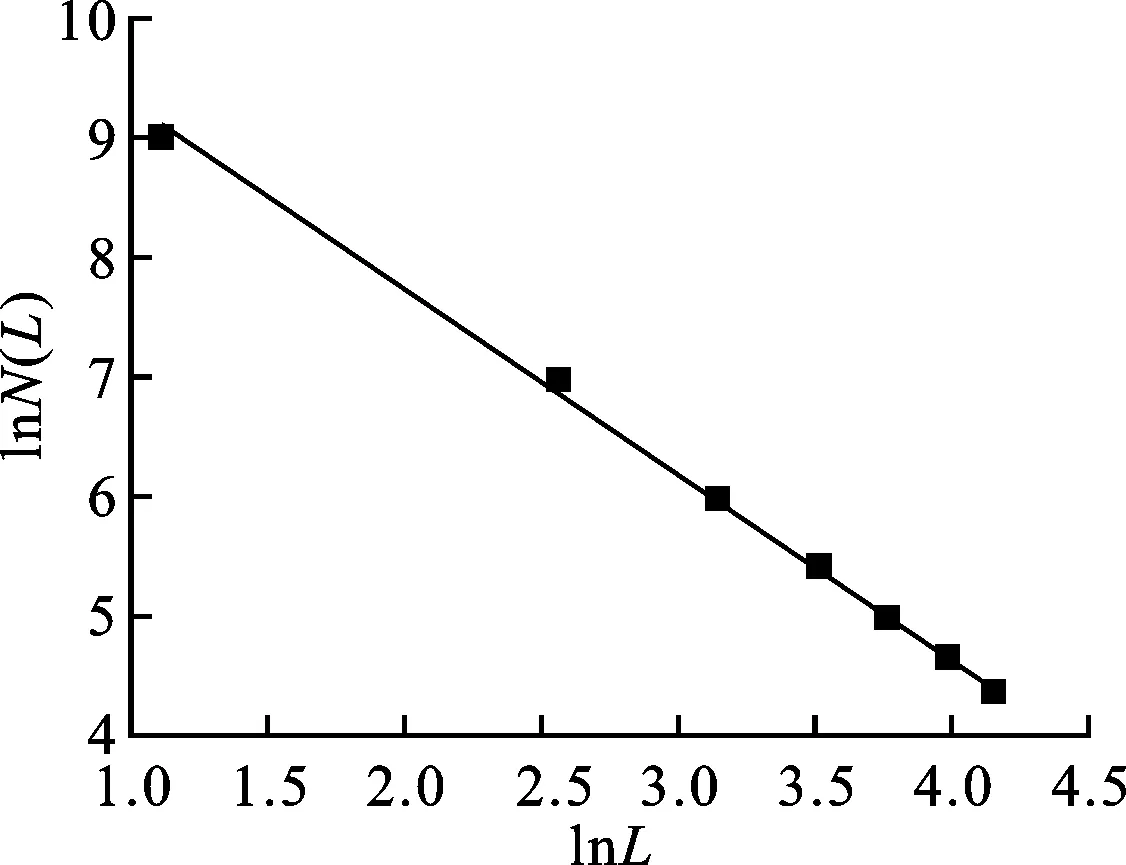
5 模型预测结果分析

6 结 论

