基于大数分解的一次性身份识别协议
李 滨
(成都师范学院 数学系 四川 成都 611130)
基于大数分解的一次性身份识别协议
李 滨
(成都师范学院 数学系 四川 成都 611130)
针对现有的身份识别协议效率不高的问题,利用大数分解的困难性和多元一次同余不定方程解的结构形式,构造了随机“询问与应答”的一个四步交互式身份识别协议.该协议符合身份证明系统的完备性、正确性、安全性和零知识性的要求,既没有被附加任何复杂性假设和用户的计算能力假设,又能做到对用户身份的一次性识别.
大数分解; 身份识别; 不定方程; 询问与应答; 协议
0 引言
身份识别是指用户向认证系统出示自己身份并证明其身份真实性或可信性的过程,通常是获得系统服务所必需的第一道关卡.在很多情况下,都需要认证系统对用户的身份进行证明.在认证系统中,用户的身份可以用三种形式来唯一识别:一是所知道的,如口令,即个人身份识别号;二是所拥有的,如智能卡、身份证等;三是所具有的生物特征,如指纹、声音等.利用密码学的方法进行身份识别,大多采用第一种方式,即用户通过出示自己掌握的某个秘密信息来证实身份.这种方式的缺点是敌手或不诚实的验证方可使用用户的身份信息来冒充用户从事非法活动.因此要求在证实身份的过程中,用户的秘密信息不能泄露.解决这个问题的办法就是利用零知识证明技术.
零知识证明[1]也是一种协议,这种协议的一方称为证明者P,它试图使被称为验证者V的另一方相信某个论断是正确的,但不向验证者提供任何有用的信息.零知识证明是交互式的,也就是证明者P和验证者V之间必须进行双向对话,才能实现零知识性,因而又称之为交互证明.交互证明是由P产生证明、V验证证明的有效性来实现,因此参与交互证明的双方之间通过某种信道的通信是必需的.利用交互证明方法做用户身份识别时,用户即为证明者,用户经过交互方式与验证者对话,设法让验证者相信他知晓某一秘密,而无需将此秘密传输给验证者,如此一来,交互式用户身份识别方法便无惧于被敌手窃听的威胁了.针对一般交互式用户身份识别协议,都必须满足以下要求:① 完备性:如果用户与验证者双方都是诚实的协议执行者,用户知道某一秘密,那么有非常大的概率,验证者将接受用户的身份.② 正确性:如果用户能以一定的概率使验证者相信他的证明,那么用户知道相应的秘密.③ 安全性:如果用户根本不知道与用户名字相关的密钥,且验证者是诚实的,那么有非常大的概率,验证者将拒绝接受用户的身份.④ 零知识性:如果用户是诚实的,那么不论协议进行多少次以及不论任何人(包括验证者)都无法从协议中推出用户的密钥,并且无法冒充用户的身份.
Fiat等[2]在1987年基于零知识证明的思想提出了一种鉴别和签名方案,两年后改进成为身份的零知识证明[3],这就是最著名的FFS身份识别协议.Dwork等[4]和Goldwasser等[5]对这个身份识别协议进行了进一步的研究,提出了该协议存在可证明结论的局限性.Schnorr[6]在1991年提出了一种计算量、通信量均较少,且特别适用于智能卡上的用户身份识别协议,其安全性建立在计算离散对数问题的困难性之上,它融合了多种方案的思想,在许多国家都申请了专利.近年来人们在与身份认证协议有关的研究方面取得了较为丰硕的成果[7-12].以上提到的身份识别协议的交互证明过程都要由若干轮组成,在每一轮,验证者都向证明者发出一个询问,证明者向验证者做出一个应答,执行完所有轮后,验证者根据证明者是否在每一轮对自己发出的询问都能正确应答,来判定证明者的身份是否有效.多轮的身份识别协议显然降低了验证的效率.作者基于大数分解的一次性身份识别协议,只需一轮“询问与应答”就能达到以上协议多轮的效果,因而更为实用.
1 预备知识
考虑如下n(n≥2)元一次不定方程:
a1x1+ a2x2+…+ anxn=M,
(1)
其中,M,a1,a2,…,an是不为零的整数系数.设gcd(a1,a2,…,an)=dn,可得引理1.

的解相同.
如果设gcd(a1,a2,…,ai)=di(2≤i≤n),那么存在整数ξ1,ξ2,…,ξn和η1,η2,…,ηn-1,满足:
可以验证
(2)
为不定方程(1)的一个特解.
定理1 设ai(1≤i≤n),N为正整数且N≠1,若gcd(dn,N)=1,则同余方程
a1x1+a2x2+…+anxn≡1 mod N
(3)
存在整数解xi(1≤i≤n)满足0≤xi≤N.


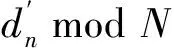

由引理1可知不定方程
使之满足0≤xi 设p, q是两个不同的大素数,N=pq, a是w的模N二次剩余,f(w,b)是w和b的整函数,即满足: a=w2mod N, f(w,b)=0 mod N. 可以看出,要想计算b就必须先计算出w,而要想计算w又必须求解二次同余方程w2mod N=a.如果把N和a公开,将p, q, w, b保密.那么求解二次同余方程w2mod N=a与分解N的素因子两者的困难性是等价的.也就是仅知道N和a,不知道w而计算b同不知道p和q而计算w同样困难.因此,证明者P以b作为自己的秘密数,通过交互证明协议,如果证明者P向验证者V证明自己的确知道b,那他便向V证明了自己的身份的确是P. 本协议的安全性依赖于计算模N平方根的困难性,这等价于大数分解的困难性.首先,假定存在一个可信任的密钥认证中心KAC,该中心的唯一作用就是秘密地选取两个模4与3同余的大数p和q,再将其乘积N公布为所有用户的模.用户P的身份信息产生过程如下: 3)公开ui(1≤i≤s),将PI(P)=(u1,u2,…,us)作为用户P的公开身份证. 这样,验证者V知道N和用户P的公开身份证PI (P).用户P想要验证者V相信他知道I(P)而不泄露它,为了达到这一点,P和V执行的“询问与应答”步骤如下: 第1步: 用户P随机地选择一个秘密整数w,使得0 第2步: 验证者V任选s个整数ei,满足1≤ei≤2t,1≤i≤s,这里t 为安全参数(一般取t =10),并将ei发送给用户P. 第3步: 用户P计算bi=wvieimod N, 1≤i≤s,并将bi发送给验证者V. 第4步: 验证者V计算 验证:若c=a,则验证者V接受用户P的身份证明.下面通过一个例子来演示一下该身份识别协议的实现过程. 例1 可信中心KAC选取p=31,q=47,则N=pq=1 457,公开N作为模. 用户P选取秘密身份信息I(P)=(v1,v2,v3,v4,v5)=(123,67,59,117,85),计算 构造同余方程 559u1+118u2+567u3+576u4+1 397u5=1 mod 1 457. 由定理1结合(2)式可得此方程在Zn上的解为 u1=1 105,u2=57,u3=1 350,u4=61,u5=1. 用户P将PI(P)=(u1,u2,u3,u4,u5)=(1 105,57,1 350,61,1)作为自己的公开身份证,并随机地选择秘密数w=1 145,计算 a=w2mod N=1 1452mod 1 457=1 182. 将a=1 182发送给验证者V.验证者随机选取5个整数组成的序列 (e1,e2,e3,e4,e5)=(23,140,19,51,108), 发送给用户P. 用户P计算 将序列(b1,b2,b3,b4,b5)=(294,553,1 385,342,302)传送给验证者V.验证者V进行如下计算: (2942×1 105×1 132+5532×57×283+1 3852×1 350×448+ 3422×61×661+3022×1×1 275) mod 1 457=1 182. 由于c=a,因此V接收P的身份证明. 从例1可以看出该协议易于实现,需要说明的是,在实际的协议应用中,出于安全考虑,大素数p和q都应在100位数以上,然而此例仅仅展示该协议的实现过程,为了便于计算,把相关的数据都取得较小. 定理2 该协议满足交互式身份识别协议的完备性、正确性、安全性和零知识性的要求. 证明 1)完备性. 如果用户P和验证者V遵守该协议且P知道I(P),则在第3步中应答bi=wvieimod N,bi一定包含w的模N二次剩余a;在该协议的第4步,V通过验证P的应答接收P的身份证明,所以该协议满足完备性. 2)正确性. 可以看出,在该协议中,当第3步用户P计算bi所采用的ei值与第4步验证者V所采用的ei值相等时,验证结果总是能使c=a成立.反之,当第3步用户P计算bi所采用的ei值与第4步验证者V计算c所采用的ei值不相等时,验证结果就不能使c=a成立. 3)安全性. 4)零知识性. 用户P没有提交他的秘密身份证,也没有向V证明他的公开身份证的合法性,而是向V显示拥有关于他的秘密身份证的知识来证明其公开身份证的合法性.在协议的第1步P发送给V的信息仅为P知道a的平方根w这一事实,并没有泄露a的平方根w,V要想通过a获取w,就必须对N进行大数分解,这在计算上是不可能的.在协议的第2步V的询问ei是从1~2t的整数中选取的,V没有机会产生其他信息.在协议的第3步的bi中P的秘密身份证I(P)是与P所选的一个随机数w混合计算,因而V无法从bi中获得I(P).综上所述,该协议满足零知识性. 本协议中秘密身份证的安全保密依赖于大数N因子分解的困难性,已知PI(P)想要求I(P)和求a的平方根w,都涉及到大数分解问题.关于大数分解问题,1994年4月底,由贝尔公司Lenstra领导的小组,大约600多人利用1 600台计算机联网,计算8个月后终于分解了长度为129位的大整数.最新记录是1999年,一个由292台计算机组成的分布式计算机网络,花了5.2个月时间完成了对一个155位的十进制大整数的素因子分解.数学家Simmons等[13]估计分解x+10位数的困难度大约是分解x位数的10倍.目前因子分解速度最快的方法,其时间复杂性函数[14]为exp(sqrt(ln(n)lnln(n))).Rivest等[15]建议取p和q为100位十进制数(≈2332),这样N为200位十进制数,要分解200位的十进制数,每秒运算107次的超高速电子计算机也要108年. 本协议是一个一次性身份识别协议,通过一轮“询问与应答”就能达到其他身份识别协议多轮“询问与应答”的效果,既符合现实中身份识别的实际要求,又节约了系统的开销,并且提高了办事效率,同时还能避免攻击者对该协议的重发攻击和交错攻击. [1]GoldwasserS,MicaliS,YaoAC.Strongsignatureschemes[C]//Proceedingsof15thAnnualACMSymposiumonTheoryofComputing.NewYork, 1983:431-439. [2]FiatA,ShamirA.Howtoproveyourself:practicalsolutionstoidentificationandsignatureproblems[C]//ProceedingsonAdvancesinCryptology.Berlin,1987:186-194. [3]FeigeU,FiatA,ShamirA.Zero-knowledgeproofsofidentity[J] .JournalofCryptology, 1988, 1(2):77-94. [4]DworkC,NaorM,ReingoldO.Magicfunctions[J].JournaloftheACM, 2003, 50(6):852-921. [5]GoldwasserS,TaumanY.OnthesecurityoftheFiat-Shamirparadigm[C]//Proceedingsof44thAnnualIEEESymposiumonFoundationsofComputerScience.NewYork, 2003: 102-115. [6]SchnorrCP.Efficientsignaturegenerationbysmartcards[J].JournalofCryptology, 1991, 4(3):161-174. [7]BonehD,BoyenX.ShortsignaturewithoutrandomoraclesandtheSDHassumptioninbilineargroups[J].JournalofCryptology, 2008, 21(2):149-177. [8]HaitnerI.Aparallelrepetitiontheoremforanyinteractiveargument[C]//Proceedingsof50thAnnualIEEESymposiumonFoundationofComputerScience.NewYork, 2009:241-250. [9]DingNing,GuDawu.Precisebounded-concurrentzero-knowledgeproofsforNP[J].ScienceChina:InformationSciences, 2010, 53(9):1738-1752. [10]ZaveruchaGM,StinsonDR.Shortone-timesignatures[J].AdvancesinMathematicsofCommunications, 2011, 5(3):473-488. [11]邓冰娜,王煜,刘宇. 一种应用于博客的垃圾评论识别方法[J]. 郑州大学学报:理学版,2011, 43(1):65-69. [12]王杰,耿丽红,朱晓东.一种改进的HMM/RBF情感语音识别方法[J]. 郑州大学学报:理学版,2012,44(4):68-72. [13]SimmonsGJ,NorrisMJ.PreliminarycommentsontheM.I.T.public-keycryptosystem[J].Cryptologia, 1977, 1(4):406-414. [14]王小云,王明强,孟宪萌. 公钥密码学的数学基础[M]. 北京:科学出版社,2013:130-135. [15]RivestRL,ShamirA,AdlemanLM.Amethodforobtainingdigitalsignaturesandpublic-keycryptosystems[J].CommunicationsoftheACM, 1978, 21(2):120-126. (责任编辑:孔 薇) One-time Identification Protocol Based on Large Numbers Factorization LI Bin (DepartmentofMathematics,ChengduNormalUniversity,Chengdu611130,China) In order to deal with the inefficient problem of the existing identification protocol, a four-step interactive identification protocol was constructed by using the difficulty of large numbers factorization and the solution constitutional formula of multivariate linear coresidual indeterminate equation. Any complexity assumption and power of prover was not relied on and any random challenge-response could be accomplished in the protocol. Some conditions of the interactive identification proof systems such as completeness and correctness as well as security and zero-knowledge were possessed by the protocol. Moreover, identification of user could be finished at one time. large number factorization; identification; indeterminate equation; challenge and response;protocol 2015-01-12 四川省教育厅科研基金资助重点项目,编号12ZB276. 李滨(1963-),男,四川富顺人,副教授,硕士,主要从事密码学研究,E-mail:1145398209@qq.com. 李滨.基于大数分解的一次性身份识别协议[J].郑州大学学报:理学版,2015,47(3):49-54. TP391 A 1671-6841(2015)03-0049-06 10.3969/j.issn.1671-6841.2015.03.0092 身份识别协议

3 协议的性能分析

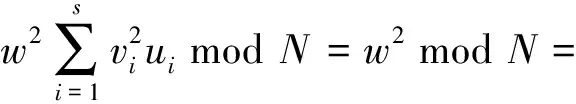
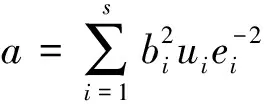
4 结束语

