可变码长LDPC码的GAU构造算法*

朱宏鹏 程 磊 张 剑

(解放军理工大学通信工程学院，南京，210007)



可变码长LDPC码的GAU构造算法*

朱宏鹏 程 磊 张 剑

(解放军理工大学通信工程学院，南京，210007)

考虑度分布、最小环长和环近似外信息度等因素，从减少短环和增加外信息度入手，提出了可变码长LDPC码的GAU(Girth-ACE union)构造算法。该算法构造的校验矩阵能适应较大范围的码长变化，其短码的纠错性能与802.16e中的LDPC码相当，中长码的性能较后者略优。不同码长的码字具有结构相同的校验矩阵，便于编译码器对所有码长采用同一架构设计，能有效降低编译码器的实现复杂度。GAU算法适用于支持可变长度数据传输的各类通信系统的LDPC码设计，具有重要的理论意义和实用价值。

低密度奇偶校验;最小环长;环近似外信息度

引 言

低密度奇偶校验(Long low density parity check, LDPC)码[1]是一类性能优越的前向纠错编码技术，其纠错性能逼近香农极限，具有较低的实现复杂度，被广泛应用于各类通信系统，如嫦娥探月工程的数据传输、GPS导航电文的播发等[2]。同一码率的LDPC码，码长越长，纠错性能越好。对于支持可变长度数据传输的通信应用，如果选用固定码长的LDPC码来进行差错控制，并非最佳选择。对于较短的数据，需要补充空字符以达到编码需要的信息长度，影响了通信的有效性；而对于较长的数据，采用较短的码长无法达到最佳的纠错能力，降低了通信的可靠性。如果采用码长可变的LDPC码，则有效性和可靠性两个方面都能较好地兼顾。构造码长可变的LDPC码，有两种方法：(1)对不同长度的码字分别进行设计，不同码长对应的校验矩阵不同；(2)对所有长度的码字基于同一个校验矩阵统一设计。方法1能够确保每种码字都具有很好的纠错性能，缺点是码型较多，实现复杂度高。方法2的优点是能够采用同一编译码架构，大大降低实现复杂度，缺点是部分码字性能无法达到最优。综合考虑纠错性能和工程可实现性，本文针对方法2，重点研究如何采用同一架构设计可变码长的LDPC码。QC-LDPC(准循环LDPC)[3]是一类非常重要的LDPC码，其校验矩阵具有准循环结构，存在线性复杂度的快速编码算法，且适合支持可变码长的统一架构设计。目前，QC-LDPC已被多个通信系统标准采用，如IEEE 802.16e，DVB-S2和802.11等。对于QC-LDPC构造的研究很多，有基于有限几何的构造算法，也有基于循环移位矩阵的构造算法。Fossorier等提出的构造算法[3]主要考虑了短环对译码性能的影响，而且针对的是规则LDPC码。相对于规则LDPC码而言，不规则LDPC码具有更好的纠错性能。本文将针对不规则QC-LDPC码，综合考虑最短环长、最短环数目和外信息度等多个因素，对QC-LDPC码进行构造，并针对不同码长对其进行适应改造，提出支持可变码长的QC-LDPC码构造算法。

1 QC-LDPC码

QC-LDPC码是一类校验矩阵具有准循环结构的LDPC码。设信息长度为k，码长为n，校验位的长度为m，m=n-k。校验矩阵定义为H，大小为m×n，其形式如下

(1)

式中：Pi,j是z×z的单位循环移位矩阵或者零矩阵。定义mb×nb的基础矩阵Hb，m=mb×z，n=nb×z,矩阵形式如式(2)所示，其中，si,j为-1～(z-1)之间的整数，称为循环移位因子。

(2)

(3)

2 GAU构造算法

基于统一架构设计可变码长的LDPC码，重点是研究如何构造基础矩阵。设QC-LDPC码的基础校验矩阵Hb的行数为mb，列数为nb。nb决定了码长的变化步径。nb越小，码长的变化分辨率越高，对可变长度的数据业务适应能力也就越好。但是，随着nb的减小，校验矩阵设计过程中可控的参数也就变少，导致码字在很多码长上纠错性能较差。nb的增加能提升码字在各个码长的纠错性能，但会减小码长的变化分辨率，同时还会增加编译码器的实现复杂度。综合考虑纠错性能、业务适应性和实现复杂度，基础矩阵的尺寸需要确定一个适中的数值。基础矩阵的构造采用半随机、半结构化的构造方法，右半部分采用第1节介绍的双对角结构，左半部分采用随机构造法。构造分为3步:度分布设计、母矩阵设计和循环移位因子构造。

2.1 度分布设计

基础矩阵的右半部分采用近似双对角结构，引入近半数度数为2的变量节点。度数较低的节点容易导致LDPC码停止集的产生[6]，从而引起纠错性能的下降。因此，需要在随机构造的校验矩阵左半部分提升度数较高的变量节点比例。根据给定的码率，结合右半部分结构化构造的度分布，在此基础上采用密度演化算法[7-8]产生最优的度分布。

2.2 母矩阵设计

母矩阵的尺寸与基础校验矩阵相同，设为mb×nb。母矩阵中的元素只有0和-1两种，0对应于基础矩阵中非负的循环移位因子，-1对应于基础矩阵中的-1。母矩阵的设计主要是确定基础矩阵中非负元素的位置。短环是导致LDPC码纠错性能恶化的关键因素之一。母矩阵的设计要尽量避免短环的产生或者减少短环的数目。根据前文介绍的度分布设计算法，可以确定母矩阵各列的度。定义母矩阵各列的度构成的集合为

(4)

式中dci为第i列的度。此外，矩阵的右半部分采用结构化设计，具有近似双对角结构，因此右半部分非负元素的位置可以直接根据双对角结构确定。本文采用PEG算法[9-11]确定母矩阵左半部分非负元素的位置。母矩阵定义为HM，行数为mb，左半部分需要构造的列数为kb=nb-mb，第i列的度数为dci，算法描述如下。

(1)初始化：母矩阵的左半部分全部初始化为-1。

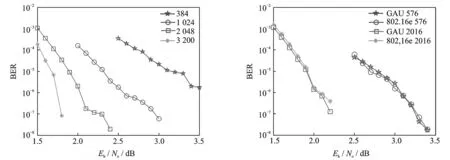
for(i=0;i

for(j=0;j

HM(i,j)=-1;}}

(2)确定非负元素位置。

for(i=0;i

for(j=0;j

①以母矩阵当前列对应的变量节点为根节点构建扩展树；

②if(树的当前层尚未涉及到所有的校验节点而下一层扩展到所有的校验节点 or当前层和下一层均未扩展到所有的校验节点，但两层涉及到的校验节点不再变化) do{

从当前层未涉及到的校验节点中寻找度数最小的节点，若存在多个度数最小的节点，则随机选取一个，设其对应的母矩阵的行号为Chk_Sel;

③HM[Chk_Sel][i]=0; }}}

2.3 循环移位因子构造算法

基础校验矩阵在母矩阵的基础之上产生，将母矩阵中的0替换为相应的循环移位因子，-1保持不变，就得到基础校验矩阵。循环移位因子的设计需要避免短环的产生。环长和循环移位因子的关系如定理1所示。

定理1[3]对于mb×nb的基础校验矩阵Hb，si,j表示第i行第j列的循环移位因子，si,j≠-1。

定义Δmx,my(nk)=smx,nk-smy,nk。当且仅当

(5)

基础校验矩阵Hb扩展得到的校验矩阵H存在长度为2i的环，其中z为扩展单位阵的大小。校验矩阵H的最小环长与循环移位因子的关系如定理2所示。

定理2[3]基础校验矩阵Hb扩展得到的校验矩阵H的最小环长不小于2(i+1)的充要条件是

(6)

式(6)满足所有的j(2≤j≤i)，所有的mk(0≤mk≤mb-1)，所有的mk+1(0≤mk+1≤mb-1)和所有的nk，其中m0=mj，mk≠mk+1，nk≠nk+1。定理1，2介绍了校验矩阵的环长与基础校验矩阵中循环移位因子之间的关系。根据定理1，遍历不同循环移位因子的过程中需要进行环长和环分布的大量统计，Mehdi Karimi等人提出了高效环长统计方法[12]，可以有效降低循环移位因子搜索过程中环长和环分布的统计复杂度。环的近似外信息度(Approximate cycle extrinsic, ACE)是影响译码性能的另一重要因素。环的ACE越大，对译码性能的改善越显著。定理3给出了环的ACE与变量节点度的关系。

定理3[13]一个长度为2i的环，其ACE如下式所示

(7)

式中：dk是环中第k个变量节点的度。

循环移位因子采用GAU构造算法，联合考虑最小环长和近似外信息度，将母矩阵左半部分kb列非负元素“0”替换为具体的循环移位因子。对于每一个非负元素，具体构造算法如下。

(1)初始化：循环移位因子初始化为0；

(2)计算校验矩阵对应的Girth，ACE和最短环数目；

(3)循环移位因子从1到z-1遍历；如果当前循环移位因子的Girth大于已选因子Girth；或者Girth相等，当前ACE大于已选因子ACE；或者Girth和ACE相等，当前最短环数目小于已选因子最短环数目；将已选因子更新为当前循环移位因子。继续遍历下一个循环移位因子。

(4)遍历完成后，已选因子即为GAU算法选取的循环移位因子。

基础校验矩阵中的循环移位因子针对可变码长中的最长码字进行设计，其他码长的基础校验矩阵与最长码的基础校验矩阵结构相同，但循环移位因子在最长码的基础上进行修改。假设最长码的基础校验矩阵第i行第j列的循环移位因子为si,j,maxlen，最长码对应的扩展单位阵的大小为zmax×zmax，当前需要构造的码字第i行第j列的循环移位因子为si,j，对应的扩展单位阵的大小为z×z，则si,j和si,j,maxlen满足如下关系式[4]

(8)

在找出最长码的循环移位因子的基础上，可以对任意扩展因子z对应的码长按照式(8)确定相应的循环移位因子，从而使设计出的基础校验矩阵适应可变码长。

3 性能仿真

设可变码长QC-LDPC码需要支持的最大码长为3 200，码率为1/2。综合考虑复杂度和纠错性能，基础校验矩阵的尺寸定为16×32。首先基于上述算法设计出码长为3 200的LDPC码基础校验矩阵，在此基础上对循环移位因子进行修改，得到码长小于3 200且变化步径长度为32的所有LDPC码的基础校验矩阵。信道选取加性白噪声高斯信道，采用BPSK调制方式，译码使用归一化最小和算法，分别对384,1 024,2 048,3 200等几个典型码长的纠错性能进行了仿真。每个码长仿真100 000次，然后统计误比特率。仿真结果如图1 所示， 五角星标记的曲线对应于 384 码长的误码性能， 圆圈标记的曲线对应于1 024码长的误码性能，正方形标记的曲线对应于2 048码长的误码性能，星号标记的曲线对应于3 200码长的误码性能。仿真结果表明，BER为10-5时，码长384的LDPC码编码增益为6.4 dB，1 024对应的编码增益为7.2 dB，2 048对应的编码增益为7.7 dB，3 200码长的编码增益为7.9 dB。码长越长，编码增益越大。IEEE 802.16e标准也支持可变码长的LDPC码，1/2码率的码长变化范围为576至2 304，图2给出了本文构造的LDPC与802.16e给出的LDPC的性能对比。选取2种典型码长，576和2 016，译码仍选用归一化最小和算法，仿真100 000次，统计误码率，仿真结果如图2所示。图中五角星标记的曲线对应于GAU算法576码长的误码性能，圆圈标记的曲线对应于IEEE 802.16e标准中576码长的误码性能，正方形标记的曲线对应于GAU算法2 016码长的误码性能，星号标记的曲线对应于802.16e标准中2 016码长的误码性能。可以看出，GAU算法构造的LDPC码与802.16e标准中的LDPC码在576码长时误码性能相当，码长为2 016时，GAU算法性能略优，且仿真中GAU算法构造的校验矩阵比802.16e适应更大范围的码长变化。综合来看，GAU算法构造的码字性能更优。

图1 几种典型码长的LDPC码误码性能 图2 GAU算法和802.16e构造的LDPC码误码性能比较Fig.1 BER of LDPC codes for several typical code lengths Fig.2 BER comparison between GAU and 802.16e

4 结束语

随着通信技术与应用的发展，越来越多的通信系统需要支持可变长度的数据传输。前向纠错编码是提高数据传输可靠性的一项有效措施，而LDPC码是近几年被深入研究和广泛应用的一类前向纠错编码。本文对可变码长LDPC码的构造算法进行了研究，综合考虑度分布、最小环长、环近似外信息度和最小环数目等因素，提出了可变码长LDPC码的统一构造方法——GAU算法。仿真结果表明，GAU算法构造的LDPC支持较大范围的码长变化，且短码和中长码都有很好的纠错性能。GAU算法对不同码长的LDPC码采用同一架构进行设计，有利于编译码器使用同一实现框架，能有效降低实现复杂度。研究成果具有重要的理论意义和实用价值。

[1] Gallager R G. Low-density parity-check codes[D]. Cambridge, MA: MIT Press, 1963.

[2] GPS Joint Program Office. Navstar global positioning system interface specification: Draft IS-GPS-800[R]. [S．l．]：Global Positioning System Directorate, 2006:26-27.

[3] Marc P, Fossorier C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004,50(8):1788-1793.

[4] LAN/MAN Standards Committee of the IEEE Computer Society and the IEEE Microwave Theory and Techniques Society. IEEE standard 802.16e 2005 amendment 2 and corrigendum 1 to IEEE standard 802.16 2004[R]. [S．l．]： IEEE， 2005:626-630.

[5] Seho M, Kyeongcheol Y, Jaeyoel K. Quasi-cyclic LDPC codes for fast encoding[J]. IEEE Transactions on Information Theory, 2005,51(8):2894-2901.

[6] Orlitsky A, Viswanathan K, Zhang J. Stopping set distribution of LDPC code ensembles[J]. IEEE Transactions on Information Theory, 2005,51(3):929-953.

[7] Wei X, AKansu A N. Density evolution for low-density parity-check codes under Max-Log-MAP decoding[J]. IEE Electron Letters, 2001,37:1225-1226.

[8] Chen Jinghu, Marc P, Fossorier C. Density evolution for two improved BP-based decoding algorithms of LDPC codes[J]. IEEE Communications Letters, 2002,6(5):208-210.

[9] Hu X Y, Eleftheriou E, Arnold D M. Progressive edge-growth tanner graphs[C]∥Proceedings of IEEE GLOBECOM 2001. San Antonio: IEEE, 2001:995-1001.

[10]Xiao H, Amir H B. Improved progressive-edge-growth (PEG) construction of irregular LDPC codes[J]. IEEE Communications Letters, 2004,8(12):715-717.

[11]傅婷婷，吴湛击,王文博.基于PEG算法的准循环LDPC码的编码构造方法[J]. 数据采集与处理，2009,24(Z1)：182-186.

Fu Tingting, Wu Zhanji, Wang Wenbo. Construction algorithm of QC-LDPC codes based on PEG algorithm[J]. Journals of Data Acquisition and Processing, 2009,24(Z1):182-186.

[12]Mehdi K, Amir H B. Counting short cycles of quasi cyclic protograph LDPC codes[J]. IEEE Communication letters, 2012,16(3):400-403.

[13]Tao T, Christopher R J, Villasenor J D, et al. Selective avoidance of cycles in irregular LDPC code construction[J]. IEEE Transactions on Communications, 2004,52(8):1242-1247.

GAU Algorithm for Construction of Variably Long LDPC Codes

Zhu Hongpeng, Cheng Lei, Zhang Jian

(College of Communication Engineering，PLA University of Science and Technology, Nanjing， 210007, China)

A girth-ACE union (GAU) construction algorithm is proposed for variably long LDPC codes considering the degree distribution, girth and approximate cycle extrinsic (ACE) message degree in a unified architecture. Therefore the short cycle number is reduced and the extrinsic message degree is increased. Large range of variable code length is accommodated through parity check matrix constructed by GAU algorithm. For short length codes, the performance of GAU algorithm is similar with that of LDPC codes in IEEE 802.16e. For middle length and long codes, GAU algorithm performs a little better. Variably long LDPC codes are designed using a common parity check matrix. The design of encoder and decoder with the same architecture for variable lengths is facilitated, which reduce the realizing complexity of encoder and decoder. Results show that the algorithm is useful in designing LDPC codes, which support variably long data communication, and the research is meaningful both in theory and practice.

low density parity check (LDPC); girth; approximate cycle extrinsic (ACE)

国家自然科学基金(61032004，91338201)资助项目。

2014-01-10；

2014-05-30

TN911.22

A

朱宏鹏(1982-),男,博士，讲师，研究方向：卫星通信，信道编码，E-mail:hongpengzhu@126.com。

程磊(1990-)，男，硕士研究生，研究方向：卫星通信。

张剑(1979-)，男，博士，讲师，研究方向：卫星通信。