高等数学习题教学改革浅谈

邵任翔，万 丽

邵任翔/广州大学数学与信息科学学院讲师，硕士（广东广州 510006）；万丽/广州大学数学与信息科学学院教授，博士（广东广州 510006）。

培养数学能力，训练非常重要。通过解题训练对于培养学生的数学能力非常有效。数学习题的组成部分包括已知条件、计算过程和实现目的。习题教学主要有以下几方面的功能。

1.学生可以通过习题课发现自己平时在学习过程中所遇到的问题，从而有针对性地补充相关的知识。

2.激发学生的学习兴趣，提高学生的解题能力。学生的解题能力提高了，有利于提升学生学习的自信心。

3.拓展和延伸学生的学习能力，激发学生的创造性。让学生自己去发现知识之间的联系，培养学生独立思考的能力，让学生养成爱思考、会思考的习惯。

发散思维（Divergent Thinking），又称辐射思维、放射思维、扩散思维或求异思维，是指大脑在思维时呈现的一种扩散状态的思维模式，它表现为思维视野广阔，思维呈现出多维发散状。不少心理学家认为，发散思维是创造性思维的最主要的特点，是测定创造力的主要标志之一。培养学生的发散思维应该是高等数学教学的主要目的之一。[1]

在习题的设计上，我们要遵循基础为主、兼顾综合的原则，做到环环相扣，逐步提高。既要有基本的练习，又要有一些跳跃性的习题，还要有一些综合性较强的练习，这样有利于学生加强实践，拓展思维，促进知识向技能的转化。

一、现阶段教材及教学所欠缺的地方

在高等数学的教材和考试中，我们习惯给出一些计算题和证明题。这两类题目所共有的特点就是：题目已经暗示你可以算出它的解析解，并且我们所要证明的命题也一定是真命题。但实际上，对于很多问题，我们无法算出它的解析解，对于很多命题，其实它本身是假命题。所以对于学生而言，他们需要明白，哪些问题其实是无法求出解析解，而只能求数值解。对于有些命题，我们事先并不知道它是真命题还是假命题，则需要我们首先做出判断，如果是真命题，需要证明；如果是假命题，需要举出反例。

我们的教材过于强调验证知识，而不是发现知识，缺少思路启发，或者说过于强调演绎推理，而不是归纳发现。知识的发现和验证都是不可或缺的重要方面，有利于提高学生们的主动创造能力。

现实的习题教学实践中，存在着这样一种值得我们注意的现象：在某种程度和范围内，教师由于对某一问题认识不足或虽然重视却又缺乏深入研究的现象，导致了在习题教学中对解题方法的基本要素的把握严重欠缺，更谈不上对其主要思想和基本方法的探索。[5]

二、对现阶段高等数学教学的一些改进

针对以上出现的问题，本人建议在例题、习题和考试中，增加以下题型，以拓展学生的发散思维。

1.错题教学。给出错题，让学生发现错误，并给出正确的解法。我们看下面这道题：

设函数在点a处具有连续的二阶导数。

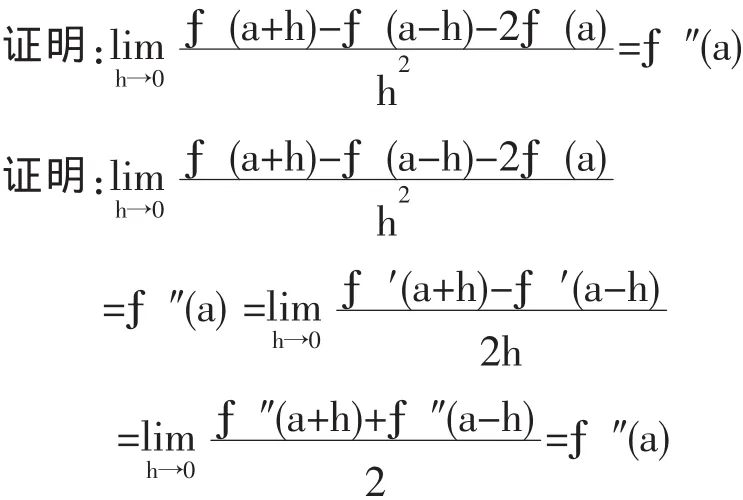
错误的原因在于f（x）在点a处二阶可导，不能推出f(x)在点a的某个邻域内存在二阶导数，故不能在第一个等式之后再用罗必塔法则。应用二阶导数的定义可以证明这道题。这种题型的好处在于不仅让学生求解或者证明一道题，而且让学生纠正错误的解法，避免以后发生相同的错误。

2.反例教学。给出命题，让学生判断对错，如果是真命题，需要证明；如果是假命题，需要举出反例。并且通过修改假命题的条件，可以把假命题更改为真命题。我们看下面这道题:

3.补充证明。对于一些较长或者较难的证明题，空出关键部分，让学生补充证明。这种题型在程序员考试中经常出现，但是在数学考试中很少出现。

我们看下面一道题：补充完整，使证明正确。

现设 M0＞0,M2＞0，利用泰勒公式，∃ξϵ( ， )，使f由此得到于是证得

这道题，大多数人应该知道证明在于构造f（x）与f″（x）的关系，但是在哪个点利用泰勒公式展开是问题的关键。这种题型的好处在于降低了证明题的难度，而在一定程度上考察了学生的自学能力，也就是现学现用的能力。这样对于一些太难的证明题也可以放到试题中去让学生补充证明。并且在改卷的时候，可以降低教师的工作量。当然，缺点在于引导学生必须按照命题者的思路解答问题。

4.一题多解。[3]在数学教学过程中适当地使用“一题多解”,不仅有利于学生创造性思维、发散性思维的培养,有利于开拓学生解题思路,提高学生灵活地、综合地运用数学知识解决问题的能力,而且有利于提高学生学习数学的积极性,提高学习兴趣等。

设f（x）在[a,b]上有连续的一阶导数,且f″（a）=求证：

证法1：因为f（x）在[a,b]上有一阶导数对于任意xϵ[a,b]，在[a,x]上使用拉格朗日中值定理可知，存在ξϵ[a,x]⊂[a,b]，使得：f（x）-f（a）=f′（ξ）(x-a)。又因为f（a）=0，所以：

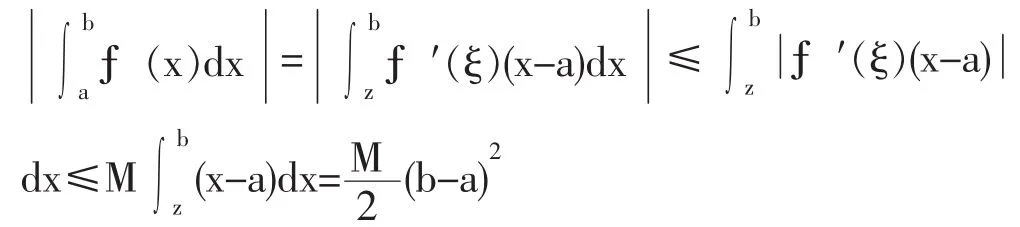
证法 2：因为f（x）在[a,b]上有一阶连续导数，而且f（a）=0，则对于任意 xϵ[a,b]，有

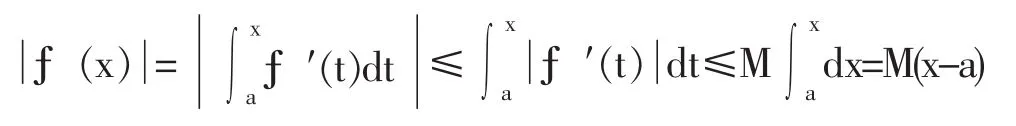
所以：

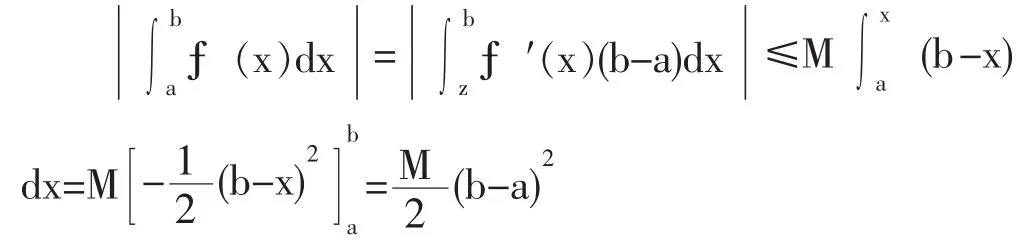
解题关键在于利用分部积分，使f（x）与f′（x）联系起来。

5.一题多变。[4]在教学中，如果我们能注意一题多变的处理，将有利于培养学生多种优良的思维品质，提高其素质，达到许多教学方式难以达到的目的。一题多变的运用主要有：更换条件与结论、改变题目的条件、增加或减少题目的条件等。下面结合在微分方程教学中讲解二阶常系数线性微分方程的解为例谈谈一题多变的应用实践。

特解形式的假设是解常系数线性微分方程的关键。我们知道“一个非齐次线性微分方程的通解=对应齐次线性微分方程的通解+非齐次线性微分方程自身的一个特解”。 并且知道 y″+py′+qy=pn(x)eλx特解形式中，Q(x)是一个与 pn(x)n有相同次数的多项式，k是一个整数:

(1)当λ不是特征根时，k=0；

(2)当λ是特征根时，但不是重根时，k=1；

(3)当λ是特征根时，且是重根时，k=2.

我们可以在求解“求方程 y″-2y′-3y=3x+1(p≠0，q≠0)的一个特解”的基础上，变化出（1）y″-2y′=3x+1(变右不变左，p≠0，q≠0)（2）y″-2y′-3y=2xex(变右不变左，λ 不是特征根)（3）y″-2y′-3y=3e-x(变右不变左，λ是特征根，但不是重根)（4）y″+y=-sin2x（±2i不是特征根）（5）y″+y=cosx(±i是特征根)。

这几道题基本包含了二阶常系数齐次线性微分方程三种类型的各种情况，使学生通过练习，不仅加深和巩固了这部分知识，而且减少了特征根的重复计算，节省了时间和精力，达到了应有的目的。

6.开放问题。所谓开放问题，是指该问题并没有唯一答案，而是促发学生思考，提出自己的看法，类似于让学生完成一篇小论文。

我们知道隐函数定理讲述了：一元隐函数的导数可以由其所对应二元函数的偏导数表示。或者说一元隐函数的某些重要性质可以由所对应的二元函数确定。但是隐函数的性质能否影响其对应的二元函数的性质呢？这类问题我们在讲述隐函数定理时极少讨论。

该问题的讨论，我们可以遵循从具体到抽象的原则。先讨论一些具体的函数，然后讨论抽象函数，判断它们的性质之间有什么联系。

比如在经济学中我们经常见到的二元效用函数y=u(x1，x2)，其所决定的一元隐函数 u（x1，x2）=c(c＜0)具有单调递减、下凸的性质。由此推断效用函数y=u(x1，x2)的一些性质。

显然二元函数y=u(x1，x2)如果具有性质：

如果一元隐函数 u（x1，x2）=c（c＞0）具有单调递减、下凸的性质，那么二元函数y=u(x1，x2)具有什么性质？显然（*）式所具有的性质不一定完全成立，但是二元函数 y=u(x1，x2)的性质必定受u(x1，x2)=c的性质制约。在这里我们可以先寻找一些具体的效用函数，比如等。我们可以先研究这些具体隐函数u（x1，x2）=c 的性质和具体二元函数 y=u(x1，x2)性质之间的联系，再去推断抽象函数性质之间的联系。

开放问题虽然不适合在考试中选用，但是非常适合学生在平时作业中完成，可以锻炼学生的创造性和发散思维。

[1]百度百科：http://baike.baidu.com/link?url=t8WhmuiAckanP3X_l_niHOdQY03hWCjZefrYrHDeWxOwOgy9v P1w69INFyr_yYknA54HSYBMEJrK98tCiEOtYK

[2]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2011.

[3]同济大学数学教研室.高等数学[M].北京:高等教育出版社,1996.

[4]李治飞,陈清江.一道积分不等式的多种证法[J].高等数学研究,2011(1).

[5]赵云河.一题多变在培养学生在求异思维中的应用[J].数学学习与研究,2012(10).

[6]杨启祥,周长军.中学数学习题教学刍议[J].科学教育创新，2008(16).