600 MW超临界W火焰锅炉流动不稳定性数值分析

沈艳荣,杨冬,王龙,谢贝贝

(西安交通大学动力工程多相流国家重点实验室,710049,西安)



600 MW超临界W火焰锅炉流动不稳定性数值分析

沈艳荣,杨冬,王龙,谢贝贝

(西安交通大学动力工程多相流国家重点实验室,710049,西安)

建立了适用于超临界锅炉流动不稳定性分析的通用数值计算模型,编写了以Fortran语言为基础的流动不稳定性数值计算程序,对程序进行验证后,采用时域法对600 MW超临界W火焰锅炉的流动不稳定性进行了模拟。计算得到了W火焰锅炉的水动力特性曲线,并研究了系统参数对其动态流动不稳定性的影响。结果表明:该模型对模拟超临界水流动不稳定性具有一定的可靠性;在0.09～0.3 kg/s的流量参数范围内,压降-流量特性曲线始终为单值关系,静态流动不稳定性不会发生;当进口压力由25 MPa增大到27 MPa或进口流量由0.091 kg/s增加到0.1 kg/s时,流量脉动的振幅逐渐减小,表明增加进口压力或进口流量锅炉的稳定性提高;当进口阻力系数由10减小到0.5或出口阻力系数由1增大到5时,流量脉动的振幅逐渐增大,表明减小进口阻力系数或增大出口阻力系数锅炉的稳定性降低。

超临界W火焰锅炉;流动不稳定性;时域法;数值分析

超(超)临界发电机组具有发电效率高、环境污染小、发电成本低等优点,目前在国内外得到了广泛的应用。由于超临界压力下锅炉水冷壁进、出口工质的密度变化很大,因此也有可能出现类似于亚临界条件下的流动不稳定现象,它不仅会引起部件的强制机械振动,还会引起管壁温度脉动,使管材疲劳失效,甚至导致传热恶化,严重威胁锅炉的安全运行。目前,国内外已经对两相流动不稳定性[1-3]进行了充分的研究,对超临界水流动不稳定性[4-5]的研究也有很多,但大多针对核反应堆,对超临界锅炉的研究很少。又由于锅炉换热结构和受热条件与核反应堆相比有很大不同,因此非常有必要对超临界锅炉的流动不稳定性进行研究。

本文建立了适用于超临界锅炉流动不稳定性分析的通用数值计算模型,编写了以Fortran语言为基础的流动不稳定性数值计算程序,针对W火焰锅炉,采用单通道的计算模型,选取水冷壁中热负荷最高、最容易发生流动不稳定的管子作为研究对象,模拟了超临界W火焰锅炉的流动不稳定性,旨在为锅炉的设计及安全运行提供指导。

1 数学模型

通常采用的流动不稳定性数值分析方法有时域法[6-7]和频域法[8-9]两种。频域法是通过将控制方程无量纲化、线性化及Laplace变换得到系统的特征方程,只能获得脉动发生时的阈值。时域法是通过对控制方程进行离散,采用数值分析方法获得脉动发生前、发生时和发生后各个参数随时间的变化,重现流动不稳定现象,有助于探索其发生机理。本文研究采用时域法。

1.1 基本假设

为简化模型,作了如下假设:

(1)采用一维近似,考虑压缩性和热膨胀性;

(2)介质与金属壁只在径向进行换热,而不考虑轴向换热;

(3)在同一截面内工质温度和速度分布是均匀的,并且管内介质只沿轴向流动,无内部环流;

(4)在能量方程中忽略黏性耗散、动能和势能的影响。

1.2 控制方程

超临界流体不再具有汽-液两相的区别,其基本控制方程与均相流动方程是相同的。

质量守恒方程为

(1)

动量守恒方程为

Kjbδd(z-zjb)

(2)

能量守恒方程为

(3)

状态方程为

ρ=f(P,h)

(4)

式中:ρ、h、M、P分别为流体的密度、比焓、质量流量和压力;A为管子横截面积;θ为流体流动方向与水平面的角度;dn为管子内径;Kin为进口阻力系数;Kex为出口阻力系数;Kjb为弯头局部阻力系数;δd为一维狄拉克函数;L为管子总长度;zjb为弯头处管子的轴向坐标;ql为线密度;f为摩擦阻力系数。本文计算采用的摩擦阻力系数计算公式是西安交通大学多相流国家重点实验室在进行了大量实验研究的基础上提出的[10-11],具有很强的实用性。

2 数值计算方法

2.1 离散方法

采用内节点法进行网格划分,采用控制容积法对方程进行离散。界面上的物性参数采用一阶迎风差分[12],即物性参数取来流方向上最后1个节点的值,在时间上采用全隐式。控制体划分如图1所示。

图1 控制体示意图

根据图1所示的控制体划分方式对控制方程离散如下。

对节点i,质量守恒方程为

(5)

动量守恒方程为

Kexδd(z-L)+Kjbδd(z-zjb)

(6)

能量守恒方程为

(7)

状态方程为

(8)

2.2 边界条件和数值计算步骤

基于单通道模型的边界条件为:①进口焓值为常数;②进口压力为常数;③进、出口压降为常数。对上述离散方程的求解可分为以下步骤。

(1)计算扰动开始前稳态流动时的压力、流量、焓值、密度沿管长方向的分布。进口压力用Pin表示,进、出口压降用ΔP0表示。对热负荷施加扰动,重复下述步骤(2)～(4),进行下一时层的计算,直至计算时间满足要求。

(3)对网格i=1,2,3,…,n-1,n,重复下述步骤(a)～(e):

2.3 程序验证

由于目前国内外对超临界水流动不稳定性实验研究的数据很少[7],因此采用数值数据来验证本文采取的数学模型和数值计算方法对模拟超临界水流动不稳定性的可靠性。目前公开发表的超临界水流动不稳定性研究文献中,Ambrosini对单通道结构进行了数值计算[13]。在相同的计算参数下,即进口压力为25 MPa、拟过冷度数NSPC为0.5、Froude数为0.03,本文程序计算结果与文献[13]的计算结果相对误差为3.2%,表明本文采用的方法对模拟超临界水流动不稳定性具有一定的可靠性。

2.4 水冷壁结构

本文计算的W火焰锅炉采用低质量流速优化内螺纹管垂直管屏水冷壁,结构如图2所示。从进口到出口水冷壁总长度为48.44 m,优化内螺纹管规格为Φ31.8 mm×6.21 mm。根据热负荷分布将水冷壁分为16个管组,长度如图2所示,每个管组内的热负荷相等,再将每个管组均匀划分为若干个管段,管段的长度即为空间网格的长度。

热负荷沿炉膛高度不均匀分布,其中AB、FG、GH段在炉膛外部为不受热段,其余为受热段。在高度19.9～21.57 m处热负荷最大,为164.95 kW/m2;在高度37.55～39.35 m处热负荷最小,为26.26 kW/m2;在炉膛中部,热负荷为114.29 kW/m2。

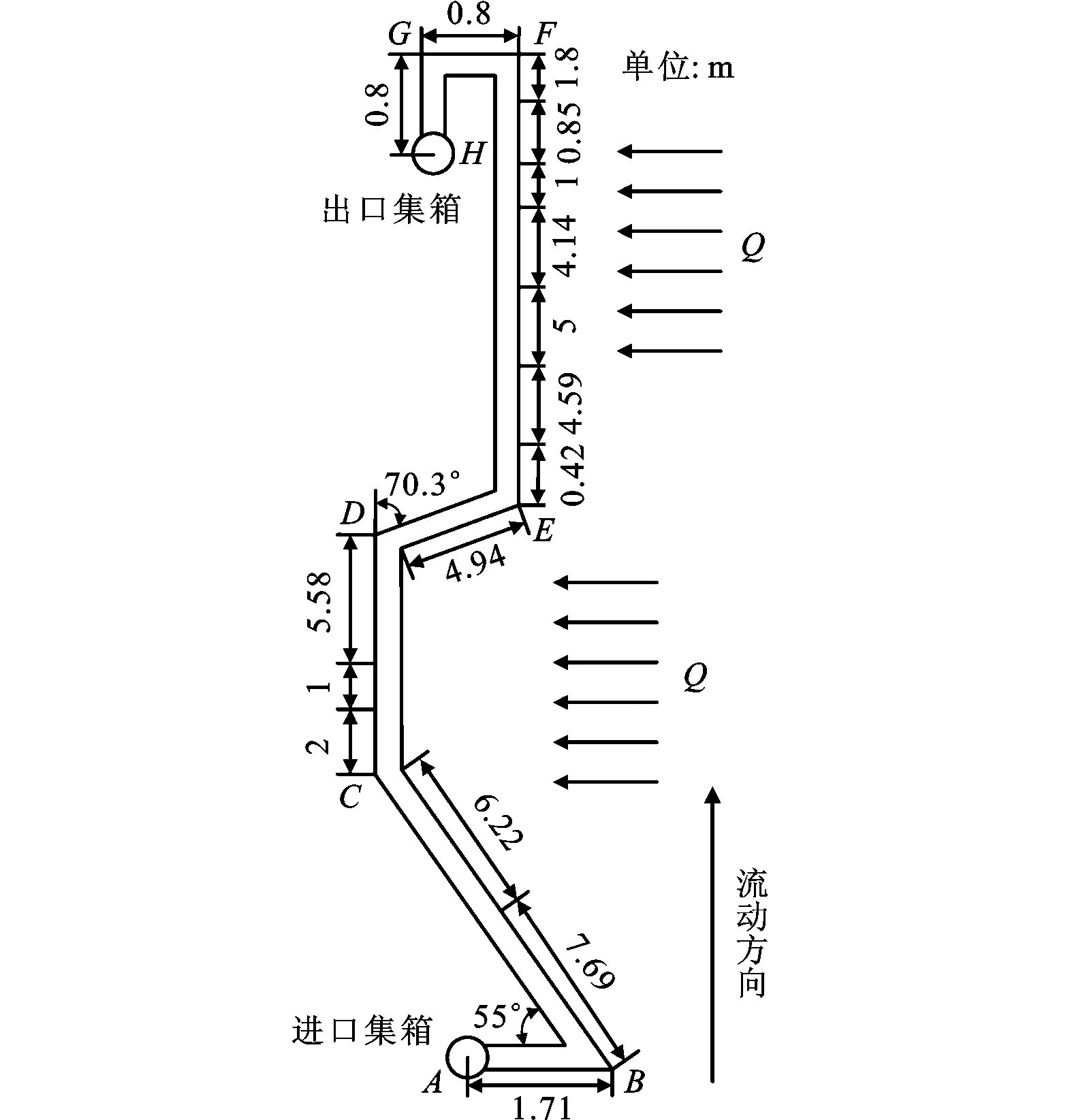
图2 水冷壁结构示意图

2.5 网格无关性分析

图3 不同时间下进口流量随时间步长的变化

图4 不同时间下进口流量随空间步长的变化

因此,在数值计算中取Δt为0.1 s、Δz为0.05 m。此时,水冷壁管划分为969个管段,节点数由进口节点1逐渐增加到出口节点970。

3 超临界W火焰锅炉不稳定性分析

3.1 静态流动不稳定性

静态流动不稳定性(流量漂移)[14]产生的原因是系统压降与流量的非单值性关系。当系统参数处于压降-流量特性曲线的负斜率区,且流量变化时系统流道压降的变化大于系统外加压力的变化,就会发生流量漂移。

图5示出了Pin为25 MPa、进口温度为280 ℃、Kin为0.5、Kex为1时的压降-流量特性曲线。由图5可以看出,水动力特性曲线在较广的流量参数范围内不存在负斜率区,压降-流量始终为单值关系,表明静态流动不稳定性不会发生。

3.2 系统参数对稳定性的影响

图6示出了稳态进口流量为0.091 kg/s,其他参数不变时不同Pin下的流量脉动曲线。图6表明,随着Pin的增大,流量脉动的振幅逐渐减小,锅炉的稳定性提高。图7示出了其他参数不变时,不同进口流量下的流量脉动曲线。图7表明,随着进口流量的增大,流量脉动的振幅逐渐减小,锅炉的稳定性提高。

图5 压降-流量特性曲线

图6 不同进口压力下的流量脉动曲线

图7 不同进口流量下的流量脉动曲线

图8示出了其他参数不变时,不同Kin、Kex下的流量脉动曲线。图8表明,减小Kin或增大Kex,流量脉动的振幅逐渐增大,锅炉的稳定性降低。

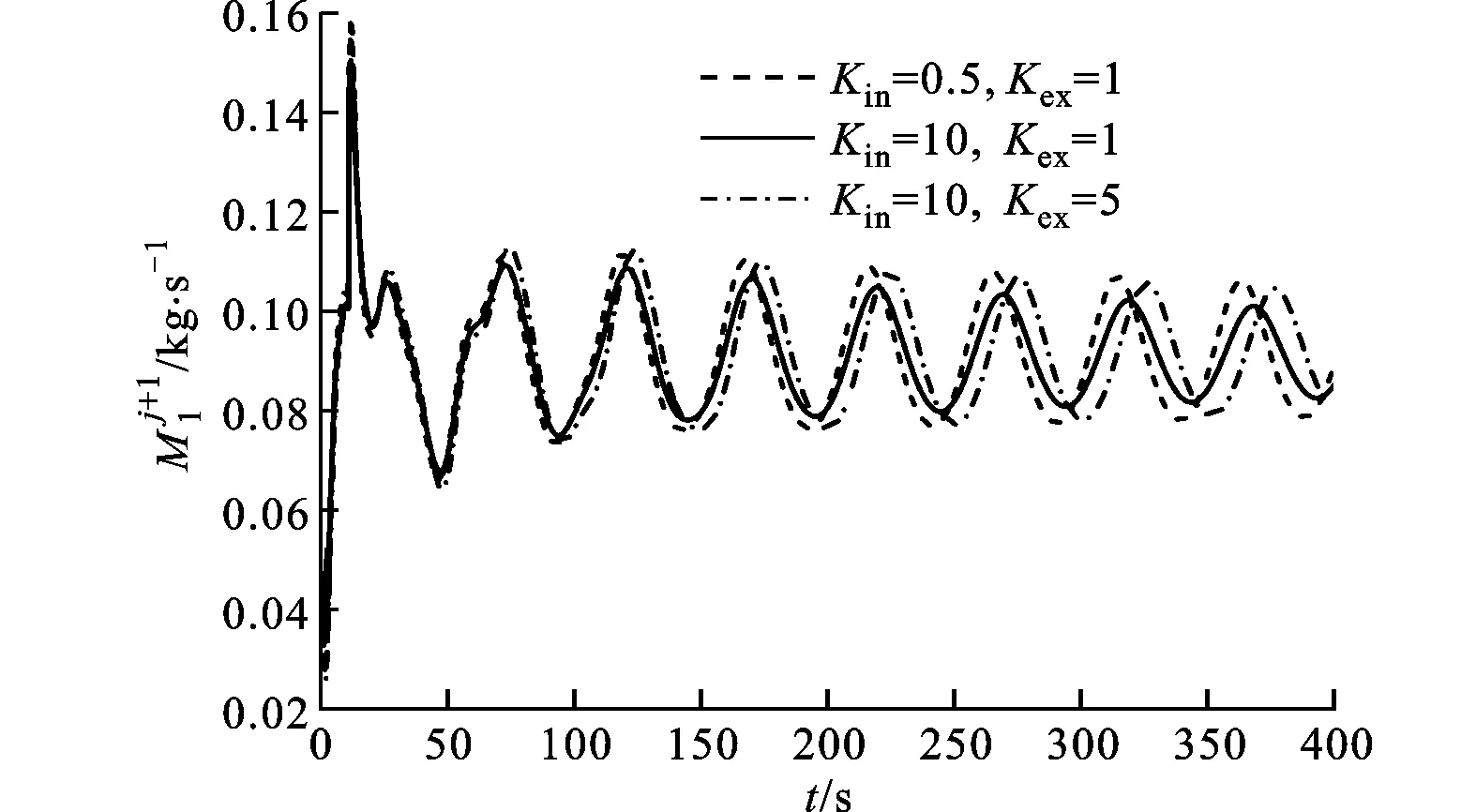
图8 不同进、出口阻力系数下的流量脉动曲线

4 结 论

(1)建立了适用于超临界锅炉流动不稳定性分析的通用数值计算模型,并编写了数值计算程序。在相同的参数条件下,与已发表文献的流动不稳定性数值计算结果进行了对比,结果符合良好,表明本文采用的模型对模拟超临界水流动不稳定性具有一定的可靠性。

(2)对600 MW超临界W火焰锅炉的流动不稳定性进行了模拟,结果表明:在较广的参数范围内,压降-流量特性曲线始终为单值关系,静态流动不稳定性不会发生;增加进口压力或进口流量锅炉的稳定性提高;减小进口阻力系数或增大出口阻力系数,锅炉的稳定性降低。

[1] DURGA P G V, PANDEY M, KALRA M S. Review of research on flow instabilities in natural circulation boiling systems [J]. Progress in Nuclear Energy, 2007, 49(6): 429-451.

[2] 黄可欣, 高峰, 毕勤成, 等. 超临界锅炉并联倾斜管内螺纹管两相流密度波型脉动数值研究 [J]. 核动力工程, 2008, 29(4): 63-69. HUANG Kexin, GAO Feng, BI Qincheng, et al. Numerical research on density wave oscillation of two-phase flow in parallel inclined internally ribbed pipes for supercritical pressure boiler [J]. Nuclear Power Engineering, 2008, 29(4): 63-69.

[3] 毕勤成, 刘伟民, 高峰, 等. U型管高压汽-液两相流动密度波型不稳定性的实验研究 [J]. 核动力工程, 2005, 26(6): 564-567. BI Qincheng, LIU Weimin, GAO Feng, et al. Experiment study on density-wave instability of high pressure steam-water two-phase flow in U-type tube [J]. Nuclear Power Engineering, 2005, 26(6): 564-567.

[4] 冯建, 田文喜, 巫英伟, 等. 超临界水并联通道流动不稳定性理论研究 [J]. 原子能科学技术, 2012, 46(4): 404-409. FENG Jian, TIAN Wenxi, WU Yingwei, et al. Theoretical study on flow instability of supercritical water in

parallel channels [J]. Atomic Energy Science and Technology, 2012, 46(4): 404-409.

[5] AMBROSINI W. On the analogies in the dynamic behaviour of heated channels with boiling and supercritical fluids [J]. Nuclear Engineering and Design, 2007, 237(11): 1164-1174.

[6] CHATOORGOON V. Stability of supercritical fluid flow in a single-channel natural-convection loop [J]. International Journal of Heat and Mass Transfer, 2001, 44(10): 1963-1972.

[7] XIONG T, YAN X, HUANG S F, et al. Modeling and analysis of supercritical flow instability in parallel channels [J]. International Journal of Heat and Mass Transfer, 2013, 57(2): 549-557.

[8] 薛爱军, 程旭. 超临界水热力系统的稳定性的简化模型分析 [J]. 核动力工程, 2009, 30(5): 35-39. XUE Aijun, CHENG Xu. Stability analysis of a simplified model of supercritical water-cooled system [J]. Nuclear Power Engineering, 2009, 30(5): 35-39.

[9] ORTEGA G T, CLASS A, LAHEY R T, et al. Stability analysis of a uniformly heated channel with supercritical water [J]. Nuclear Engineering and Design, 2008, 238(8): 1930-1939.

[10]张伟强, 李会雄, 张庆, 等. 内螺纹管内超临界水的流动阻力特性试验研究 [J]. 中国电机工程学报, 2013, 33(7): 1-7. ZHANG Weiqiang, LI Huixiong, ZHANG Qing, et al. Experimental study on flow resistance of supercritical pressure water in an internally ribbed tube [J]. Proceedings of the CSEE, 2013, 33(7): 1-7.

[11]潘杰, 杨冬, 肖荣鸽. 低质量流速优化内螺纹管摩擦阻力特性实验研究 [J]. 高技术通讯, 2014, 24(4): 429-423. PAN Jie, YANG Dong, XIAO Rongge. Experimental investigation on frictional resistance characteristics of optimized rifled tube at low mass flux [J]. Chinese High Technology Letters, 2014, 24(4): 429-423.

[12]陶文铨. 数值传热学 [M]. 2版. 西安: 西安交通大学出版社, 2011: 140-141.

[13]AMBROSINI W. Assessment of flow stability boundaries in a heated channel with different fluids at supercritical pressure [J]. Annals of Nuclear Energy, 2011, 38(2/3): 615-627.

[14]张项飞. 超临界压力下自然与强制循环回路水动力特性分析 [D]. 上海: 上海交通大学, 2012.

(编辑 荆树蓉)

Numerical Analysis on the Flow Instability of a 600 MW Supercritical W Flame Boiler

SHEN Yanrong, YANG Dong, WANG Long, XIE Beibei

(State Key Laboratory of Multiphase Flow in Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A general numerical computational model suitable for the analysis of supercritical boiler instability was established, and the numerical computational program based on Fortran was developed. Then the flow instability of a 600 MW supercritical W flame boiler was simulated by the time-domain method after the model and code were verified. The curve of pressure drop versus flow rate was obtained and the parametric effects on the dynamic instability of the W flame boiler were analyzed. The results showed that the model is reliable to simulate the supercritical water instability; the curve of pressure drop versus flow rate is always an one-on-one relationship at the flow rate range from 0.09 to 0.3 kg/s, which means the static flow instability does occur; when the inlet pressure increases from 25 to 27 MPa or the inlet flow rate increases from 0.091 to 0.1 kg/s, the amplitude of flow rate oscillation decreases, indicating that increasing inlet pressure or inlet flow rate will improve the boiler’s stability; when the inlet pressure drop coefficient decreases from 10 to 0.5 or the outlet pressure drop coefficient increases from 1 to 5, the amplitude of flow rate oscillation increases, indicating that decreasing the inlet pressure drop coefficient or increasing the outlet pressure drop coefficient will reduce the boiler’s stability.

supercritical W flame boiler; flow instability; time-domain method; numerical analysis

2014-09-17。

沈艳荣(1988—),女,硕士生;杨冬(通信作者),男,教授。

中国科学院战略先导科技专项资助项目(XDA07030100)。

时间:2015-02-27

10.7652/xjtuxb201505011

TK122

A

0253-987X(2015)05-0068-05

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150227.1724.015.html