一种改进的图像压缩感知稀疏恢复算法*
杨三加,谢正光,张 峥,姜欣玲
(南通大学 电子信息学院,江苏 南通 226019)
1 引言
近些年发展起来的压缩感知技术(Compressed Sensing,CS)[1-2]突破了Nyquist 采样定理的瓶颈,可以用低于Nyquist 采样定理所需的采样速率对信号进行采样。目前,CS 主要由信号的稀疏表示、观测矩阵设计以及恢复算法三部分组成,恢复算法是CS 理论中至关重要的组成部分,它直接影响信号的重构质量。
现阶段恢复算法主要有贪婪算法[4-5]、凸优化算法[6]和Bayesian 方法[8-11]。基于Bayesian 方法的稀疏信号重构首先将促进稀疏性的先验概率分布赋予未知信号,然后从压缩测量值中推断未知系数的后验分布。2009 年,Malkei 以Bayesian 方法为基础,用拉普拉斯分布逼近信号分布,推导出的近似信息传递算法(Approximate Message Passing,AMP)[3]不仅有迭代阈值类算法的低复杂度,而且在数据量充分大的情形下重建信号的能力与基追踪(Basis Pursuit,BP)[12]相当。2010 年,Sudeep Rangan[8]提出的广义近似信息传递算法(Generalized Approximate message,GAMP)是对AMP 的推广,它可以处理任何可因子分解的信号和噪声分布。由于并不能预先知道信号和噪声模型,因此Jeremy Vlia 和Philip Schniter 用贝努力高斯模型(Bernoulli Gaussian,BG)和高斯混合模型(Gaussian Mixture,GM)逼近信号,零均值的高斯白噪声逼近噪声,采用期望最大值算法(Expectation Maximization,EM)[13]估计信号模型中的参数,得到期望最大贝努力高斯近似信息传递算法(Expectation Maximization Bernoulli Gaussian Approximate Message Passing,EM-BG-AMP)[9]和期望最大高斯混合近似信息传递算法(Expectation Maximization Gaussian Mixture Approximate Message Passing,EM-GM-AMP)[10]。但是,他们只考虑了对一维信号的重建,并没有考虑二维图像信号。
若图像的稀疏基是小波,不同分解级数不同方向小波系数的稀疏率、均值和方差并不相同。用EM-BG-AMP 重构图像,近似系数和每级各个方向细节系数的BG 模型参数相同,降低了模型参数估计的精确性。因此,本文根据图像在小波基下系数的分布特点,提出了期望最大分段贝努力高斯近似信息传递算法(Expectation Maximization Separately Segment Bernoulli Gaussian Approximate Message Passing,EM-SSBG-AMP),将小波分解后的近似系数与每级的水平、垂直、对角细节系数的BG 模型参数分开估计,提高了模型参数估计的精确性。
2 图像小波域BG 模型参数分段估计
2.1 基本思想
图像经小波变换[14]后,小波系数的幅值在尺度间呈指数形式下降,且不同分解级数不同方向小波系数的稀疏率、均值、方差有着较大的差异。用BG逼近小波系数,每级各个方向小波系数的稀疏率、均值、方差不应相同。因此,本文在使用EM 更新BG模型参数时,将近似系数与各级的水平、垂直、对角细节系数的模型参数分开估计,以提高估计参数的精确性。
2.2 期望最大分段贝努力高斯近似信息传递
进行S 级小波分解的图像可将BG 模型参数分为3S+1个数据段估计。设3S+1个数据段的索引集合为I={s(1),s(2),…,s(3S+1)},s(1)是近似系数索引集,其余的是各级细节系数的索引集。集合F={ls(1),ls(2),…,ls(3S+1)}中每个元素表示I 中每个索引集包含元素的个数。数据段l 中第i个元素θs(l)(i)的BG 模型表示如下:
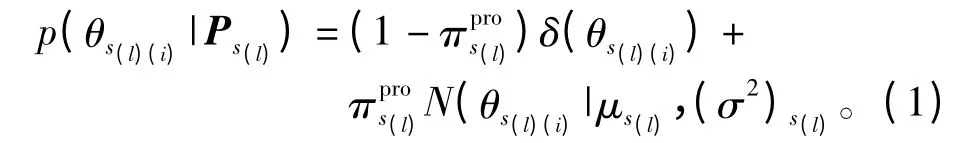
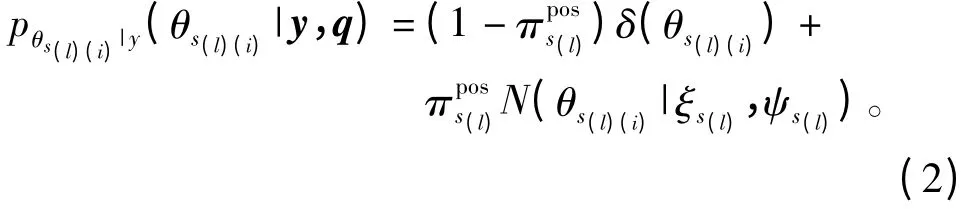
由文献[9-10]以及本文的研究思路可得第l数据段下Ps(l)中每个参数的EM 更新方式:
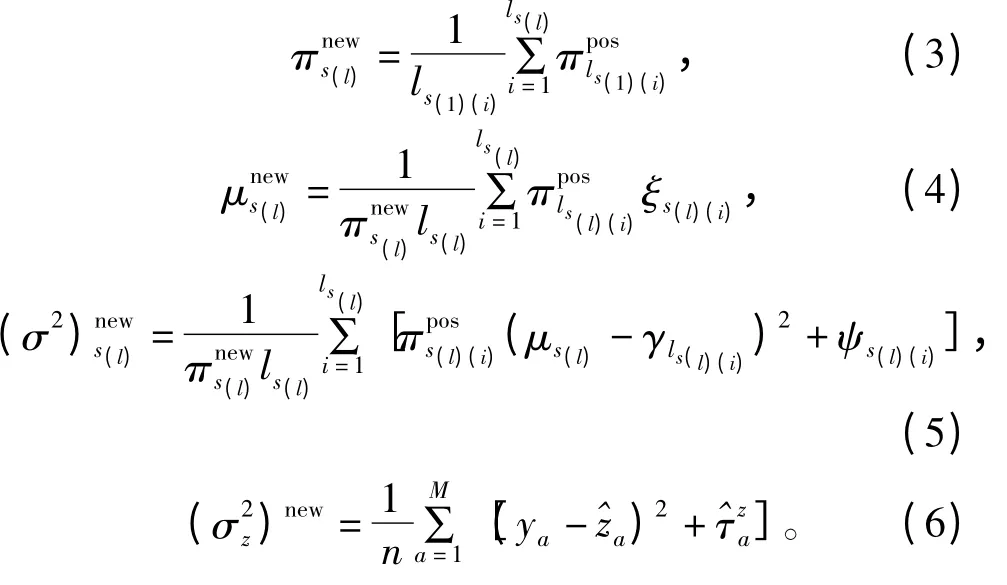
图1 为本文所提算法EM-SSBG-AMP 框图。
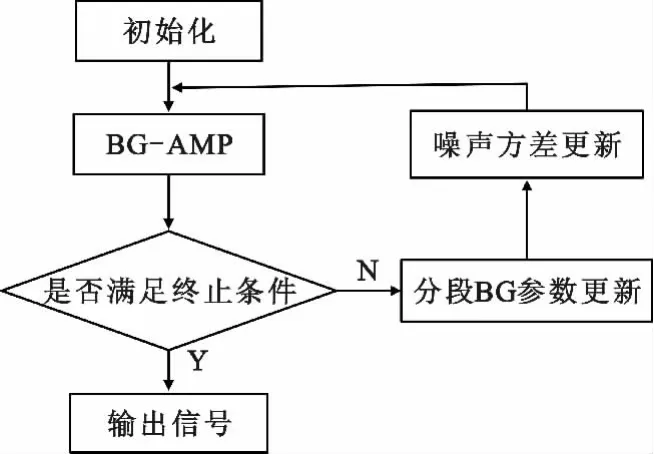
图1 EM-SSBG-AMP 流程框图Fig.1 Block diagram of EM-SSBG-AMP
EM-SSBG-AMP 算法的详细步骤如下:

判断是否满足迭代终止条件:E <Etol‖K <Kmax,满足则跳出循环,不满足则用EM 对近似系数和各级细节系数的参数进行更新:

ρSE(δ)是理论上l1最小范数相移曲线[9]。从EM-SSBG-AMP 的详细步骤可看出EM 更新过后近似系数与每级各个方向细节系数的模型参数并不相同,提高了估计参数的适应性,而文献[9]和[10]在EM 更新后所有模型参数相同,并不符合图像小波分解后系数分布的真实情形。
3 实验仿真与结果分析
为评价模型的性能,选取具有代表性的大小为128 ×128 纹理不同的Barbara(纹理复杂)、Lena(纹理适中)与Fruits(纹理简单)3 幅自然图像做为测试对象。图像恢复后的客观评价指标峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)定义为
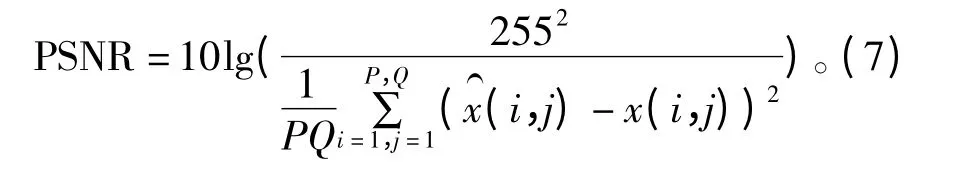
3.1 实验环境
为便于公平比较不同算法的重建性能,实验环境及参数的设置基于文献[9-10]。仿真平台为Matlab 2012b,CPU 为3.47 GHz、内存为24 GB 的Windows 7 HP 台式机。
对二维图像的测量,仅列出以小波函数db1、分解级数S=4 为例的测试结果,其他不同小波函数或分解级数也可以使用。实验中将变换后的小波系数排列成一个列向量θ,其维数N=128 ×128。欠采样率δ 定义为n/N,分别取典型值0.2、0.3、0.4、0.5进行比较。测量值个数n=δN。列归一化的测量矩阵Φ∈Rn×N服从均值为0、方差为1/M 的高斯分布。Kmax=10、Etol=10-5与文献[9-10]相同。为保证重构概率的准确性,用相互独立的500个测量矩阵Φ 分别对以上3 幅图像进行测量与重构,评价指标取平均。
3.2 结果与分析
因高斯模型的阶数大于5 时算法复杂且PSNR增加较小,所以本实验仅与3 阶和5 阶EM-GM-AMP(表示成EM- GM(3)- AMP,EM- GM(5)-AMP)以及未分层估计的EM-BG-AMP 进行比较。
从表1 中可以明显看出,所提算法EM-SSBG-AMP 的PSNR 明显高于EM- BG- AMP、EM-GM(3)-AMP 和EM-GM(5)-AMP。纹理越复杂,EM-SSBG-AMP 的优势越明显,如当采样率为0.5 时,对于Barbara、Lena 和Fruits,EM- SSBG-AMP 的PSNR 比EM- GM(5)- AMP 依次高1.96 dB、1.76 dB、1.56 dB。而随着采样率的增高,EM-SSBG-AMP 与EM-GM(5)-AMP 之间的差值呈现出一种非增趋势,比如对于纹理较简单的Fruits,在采样率为0.2、0.3、0.4、0.5 时EM-SSBG-AMP 比EM- GM(5)- AMP 分别高1.67 dB、1.62 dB、1.61 dB、1.54 dB。也就是说,采样率越低时,EM-SSBG-AMP 的优势越明显。图2 给出了每幅图像的PSNR 曲线,以便更直观地比较每幅图像在不同的采样率下的PSNR 变化趋势。

表1 采样率为0.2、0.3、0.4、0.5 下不同算法重建图像实验结果Table 1 Reconstructed image simulation results when sampling ratio is 0.2,0.3,0.4,0.5,respectively
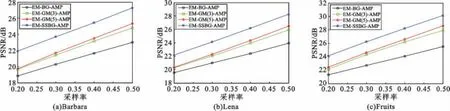
图2 采样率为0.2、0.3、0.4、0.5 下不同算法重建图像的PSNR 曲线Fig.2 The PSNR curve of reconstructed image when sampling ratio is 0.2,0.3,0.4,0.5,respectively
从表1 中同时可以看出对3 幅测试图像,EMSSBG-AMP 所用的时间比EM-BG-AMP 略高,高出的时间是每次分层估计寻找索引增加的时间。与EM-GM(3)-AMP 和EM-GM(5)- AMP 相比,EM-SSBG-AMP 所用的时间略少。图3 给出了3 幅图像不同采样率下的时间曲线,以便更直观地比较时间变化趋势。
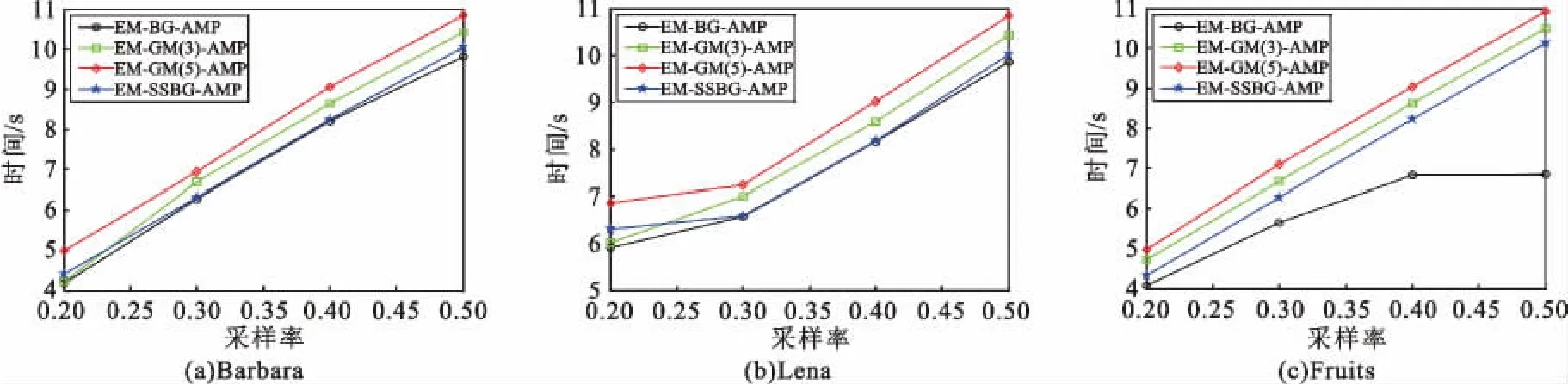
图3 采样率为0.2、0.3、0.4、0.5 下不同算法重建图像时间曲线Fig.3 The time curve of reconstructed image when sampling ratio is 0.2,0.3,0.4,0.5,respectively
为了比较重构图像的视觉效果,图4~6 为采样率为0.5,EM-BG-AMP、EM-GM(5)-AMP、EM-SSBG-AMP 重建Barbara、Lena、Fruits 的视觉效果图。从图4~6 可看出,本文所提算法较EM-BG-AMP 和EM-GM(5)-AMP 重建纹理清晰,没有明显的块效应。

图4 采样率为0.5 不同算法重建Barbara 图像Fig.4 Reconstructed Barbara image by different algorithms when sampling ratio is 0.5

图5 采样率为0.5 不同算法重建Lena 图像Fig.5 Reconstructed Lena image by different algorithms when sampling ratio is 0.5

图6 采样率为0.5 不同算法重建Ftuits 图像Fig.6 Reconstructed Fruits image by different algorithms when sampling ratio is 0.5
从以上的比较与分析可知,对分开估计BG 模型参数的EM-SSBG-AMP 重建图像的PSNR 和视觉效果明显优于EM-BG-AMP,提高了模型参数估计的适应性。与3 阶和5 阶的EM-GM-AMP 相比,EM-SSBG-AMP 的PSNR 和视觉优势明显,而时间相当。同时,EM-SSBG-AMP 重建纹理复杂的图像优势更为明显。在实际应用中,将不同分解级数不同方向的小波系数模型参数分开估计,易于实现。
4 结束语
本文提出的EM-SSBG-AMP 分开估计图像小波分解后的近似系数与每级各个方向细节系数的模型参数,提高了参数估计的适应性,它适用于稀疏变换系数分布不均匀的图像。相同采样率下,EMSSBG-AMP 重建图像的时间比5 阶EM- GM-AMP 少,PSNR 比5 阶EM-GM-AMP 高,纹理复杂度越高,EM- SSBG- AMP 重建图像的PSNR 比5阶EM-GM-AMP 高得越多。下一步的研究方向是利用小波系数尺度间、尺度内的相关性来提高模型参数估计的适应性以及进行算法的抗噪声性能研究。
[1]Candes E,Romberg J,Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[2]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[3]Donoho D L,Maleki A,Montanari A.Message Passing Algorithms for Compressed Sensing[J].Proceedings of the National Academy of Sciences,2010,106 (45):18914-18919.
[4]Wu D,Zhu W P,Swamy M N S.The theory of compressive sensing matching pursuit considering time domain noise with application to speech enhancement[J].IEEE Transactions on Audio,Speech,and Language Processing,2014,22(3):682-696.
[5]Chang L,Wu J.An Improved RIP-Based Performance Guarantee for Sparse Signal Recovery via Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory,2014,60(9):5702-5715.
[6]Rao B D,Engan K,Cotter S F,et al.Subset selection in noise based on diversity measure minimization[J].IEEE Transactions on Signal Processing,2003,51 (3):760-770.
[7]Donoho D L,Javanmard A,Montanari A.Information theoretically optimal compressed sensing via spatial coupling and approximate message passing[J].IEEE Transactions on Information Theory,2013,59(11):7434-7464.
[8]Rangan S.Generalized Approximate Message Passing for Estimation with Random Linear Mixing[J].Eprint Arxiv,2010,42(4):2168-2172.
[9]Vila J,Schniter P.Expectation maximization Bernoulli Gaussian approximate message passing[C]//Proceedings of 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals,Systems and Computers.California,USA:IEEE,2011:799-803.
[10]Vila J,Schniter P.Expectation Maximization Gaussian Mixture Approximate Message Passing [J].IEEE Transactions on Signal Processing,2013,61 (19):4658-4672.
[11]Wu S,Kuang L,Ni Z,et al.Expectation propagation approach to joint channel estimation and decoding for OFDM systems[C]// Proceedings of 2014 IEEE International Conference on Acoustics,Speech and Signal Processing. Washington,USA:IEEE,2014:1941-1945.
[12]Zhang X W,Ming L,Lei Z.Sparse Signal Reconstruction Based on Basis Pursuit Moore Penrose Inverse Matrix[J].Journal of Electronics & Information Technology,2014,35(2):388-393.
[13]Demrsrsa A P,Lamb N M,Rubin D B.Maximum likelihood from incomplete data via the EM algorithm[J].Journal of the Royal Statistical Society Series B(Methodological),1977,39(1):1-38.
[14]Zhang Y,He Z,Zhang Y,et al.Global optimization of wavelet domain hidden Markov tree for image segmentation [J].Pattern Recognition,2011,44 (12):2811-2818.

