空间复用认知无线电系统信道选择优化*

刘 颖，穆晓敏，师光强

(郑州大学 信息工程学院，郑州 450001)

1 引言

随着异构网络的快速增加，频谱资源变得更加匮乏，已经成为制约无线通信发展的瓶颈，如何提高频谱资源利用率成为5G 亟待解决的问题，因此，动态频谱接入技术应运而生［1－2］。动态频谱接入的关键挑战是如何解决分布式频谱资源分配，如果用户位置足够远，它们可以同时在同一频带传输且不会造成任何性能退化，借此提高频谱利用率［3］。相比其他多用户资源优化方法，博弈论能从系统角度反映多用户之间的相互影响，预测系统的稳定状态(即均衡点)，从而指导用户决策以提高系统性能［4］。

纵观现有的大部分研究，所建立的动态频谱接入博弈模型都忽略了用户所处的空间位置，认为每个用户的决策都对其他所有用户有影响［5－6］。然而，这个假设只适用于网络规模较小且用户分布比较集中的情形。在一般无线接入网中，接入用户在空间位置上任意分布且用户的决策只影响与其相邻的用户，这可能对频谱效率及动态频谱共享机制带来很大的影响。因此，近年来，如何构建基于空间位置的优化问题激发了人们的研究兴趣，并出现了少量的研究成果［7－9］。这些研究成果提出了机会频谱接入优化框架，根据不同的目标函数设计相应的优化框架。文献［7］提出了以最大化网络吞吐量期望值为目标函数的优化框架，在信道空闲概率和认知用户个数未知的情况下，假设业务需求相同，研究了信道选择策略集合的优化问题，但实际系中空间位置信息不同和业务需求不同都对最优信道选择集的确定有影响。鉴于此，文献［8］提出了以最小化系统干扰为目标函数的优化框架，在此框架下，认知用户根据空间位置决定的干扰图评估干扰，优化信道选择策略集合，但为考虑业务需求的不同。随后，文献［9］提出了以最大化期望吞吐量为目标函数的优化框架，联合优化用户位置和信道选择策略集合。

在基于空间复用的机会频谱接入模式下，空闲信道速率(或带宽)不一致也是影响系统机会接入吞吐量和最优信道集合的关键因素之一，系统谱效与机会频谱接入收敛速度均与其有关。然而，上述文献均未考虑信道速率不一致的情形，为此，本文在文献［8］的基础上以最大化系统吞吐量为优化目标，基于博弈模型，研究了分布式信道带宽不同的场景下信道集的选择问题，证明了该优化问题是至少具有一个纯策略纳什均衡的精确势能博弈，并且其纳什均衡点是问题的全局最优解。仿真结果表明，本文提出的基于博弈模型的分布式信道选择问题存在纳什均衡解，相对于文献［8］，考虑空间复用后，系统吞吐量增大，频谱利用率显著提高。

2 分布式网络信道选择与干扰图描述

考虑认知网络用户空间位置分布可能提供空间复用频谱接入机会，由认知无线电网络分布可以得到相应的干扰图［8］，用来描述干扰的有限范围，涉及N个认知用户，在授权用户不使用授权信道时机会接入信道;同时涉及M个授权信道，可以随机被授权用户使用;非对称信道速率Rm随信道的改变而改变，1≤m≤M，N ＞M ＞1。图1 举例说明了两个授权用户、4个授权信道(1，2，3，4)、5个认知用户的认知无线网络分布及对应的干扰图。

图1 基于空间复用机会频谱接入的说明Fig.1 Illustration of opportunistic spectrum access with spatial reuse

频谱可用机会随着用户位置的改变而改变，则用可用信道矢量Cn来描述异构频谱机会，特别地，对于每个用户n∈N，Cn={Cn1，Cn2，…，CnM}，Cnm=1，m∈M 表示信道m 可以被用户n 选择即授权用户没有使用信道m，Cnm=0 表示信道m 不可以被用户n 选择即授权用户使用了信道m，此外假设频谱机会的时间是静态的。假设认知用户的位置属于一个空间集合D 即频谱可能接入位置的集合。dn∈D 表示认知用户n 的位置，d=(d1，d2，…，dN)∈DN表示所有用户的位置集合，认知用户有一个干扰范围δ。当给出所有用户位置集合d，可根据干扰图用Gd={N，εd}来描述认知用户之间的干扰关系。顶点集N 表示认知用户的集合，边缘集εd={(i，j):‖di，dj‖≤δ，i，j≠i∈N}表示干扰边的集合。如果两个认知用户之间存在边缘集，那么这两个认知用户不能成功地同时用同一个信道传输数据，因此用Jn={j∈N，(j，n)∈εd}表示用户n 的干扰用户集合即相邻用户集合。

由图1 中无线认知网络部署对应的干扰图可以看出，相邻用户之间同时在相同信道传输时才会产生干扰，且认知用户的传输与空间复用的可能性是与用户的空间位置有关的，因此，基于干扰图研究空间复用时频谱共享的性能以及进一步挖掘频谱效率是很有必要的。

3 基于博弈论的信道选择优化问题

研究基于空间复用的频谱共享机制首先要分析其频谱利用率和用户接入策略，频谱利用率通常用认知用户系统吞吐量来建模，并通过设计用户接入策略集最大化系统吞吐量。该问题是一个典型的组合优化问题，且该网络模型没有中心控制器，为此，我们采用博弈论对其进行建模求解。然而，以往精确势能博弈都是在信道速率一致的前提下提出的，因此，在信道速率不一致的条件下，如何建立精确势能博弈急需解决。

3.1 基于空间复用频谱共享优化问题建模

假设所有认知用户可以完美地感知所有信道，且每个认知用户只能在一个信道上进行传输。利用高效的分布式方式例如CSMA 机制应用于相互干扰的相邻用户之间的数据传输，在信道速率不一致的条件下，固定信道空闲概率，则用户n 基于空间复用的吞吐量表示如下:

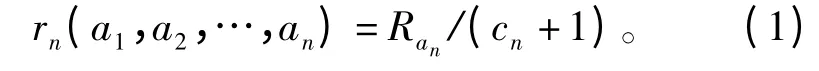
由于不同的信道带宽会使信道速率不一致，因此，为了简单起见，假设=R/an，其中an表示用户n 选择的信道。表示认知用户n相邻认知用户竞争的个数，g(x，y)是指示函数即

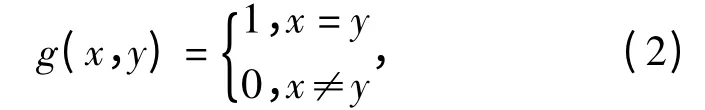
因此，系统吞吐量可以表示如下:

本文研究的目标是找到一个最优的信道选择集合使系统吞吐量达到最大，即

可以看出，P 是一个典型的组合优化问题且是NP 问题［10］。在集中式中运用穷举法可得到最优信道集合但有很高的复杂度;启发式方法［11］是可供选择的方法，但它无法获取最优信道选择，因此，在认知无线电网络中，迫切需要一个能获取分布式最优信道集合的具有低复杂度的方法。

3.2 基于博弈论的优化问题求解

通过上节的分析，我们将基于空间复用的频谱共享优化问题建模为最优信道集合选择问题。由于没有中心控制器，每个认知用户都是自私的，只关心自身效用函数最大化，这就促使我们关于这个问题建立博弈模型，一般情况下，博弈模型的纳什均衡不能使系统效用函数最优。因此，为了获得系统效用函数最优，本小节提出针对分布式信道选择问题以每个用户吞吐量倒数的负数为效用函数的博弈模型，并证明其是至少存在一个纳什均衡的精确势能博弈，且其纳什均衡点是最大化系统吞吐量优化问题的最优信道选择集合。

(1)效用函数

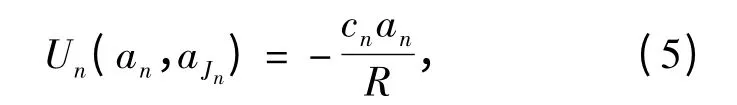
因此，该博弈可以描述如下:

式中，An是参与者n 的策略集(用户n 可用信道集合)，An={m∈M:Cnm=1}。

G 是至少具备一个纳什均衡的精确势能博弈，并且其纳什均衡点是P 的最优解。

证明:构建一个势能函数如下:

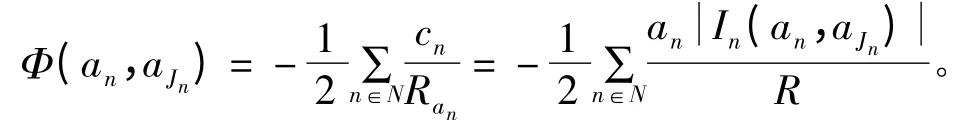
式中，In(an，aJn)={j∈Jj:aj=an}表示参与者n 相邻用户选择相同信道的集合，则cn=。假设任意用户单方面改变策略从an到a*n，势能函数的改变如下:

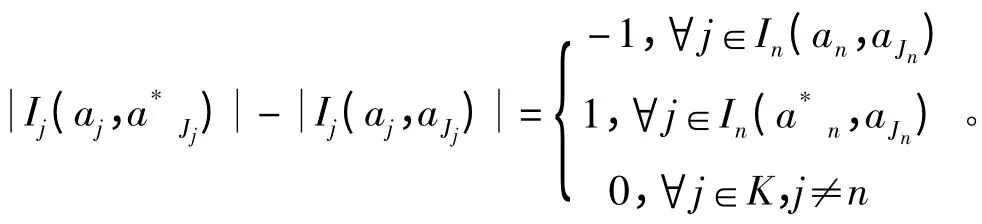
另一方面，假设任意用户单方面改变策略从an到，效用函数的改变如下:

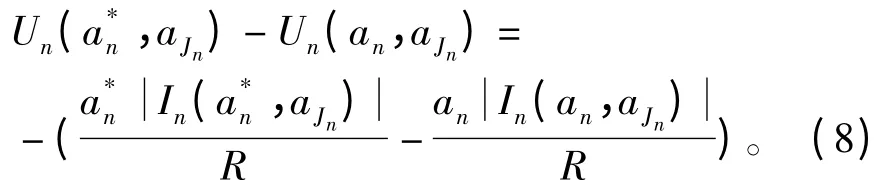
从式(7)到式(8)，可以得到

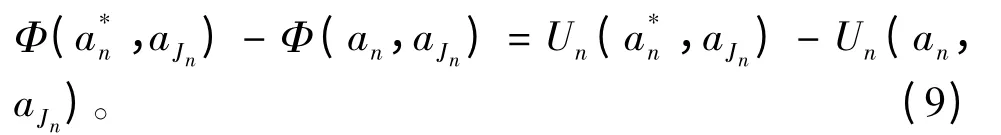
根据式(9)可以看出该博弈是精确势能博弈［9］。精确势能博弈有如下的性质:任何精确势能博弈至少具有一个纯策略纳什均衡;势能函数全局或局部最大点是该精确势能博弈的纳什均衡。

定理得证。

3）单位应该赋予检查部门足够的处罚权利。单位应将安全摆在第一位，制度上明确检查部门的权利及被检查对象的义务，充分树立检查部门的权威。可允许检查者参照交警执勤方式，不留情面、现场开具罚单，且列入年终考评，使违者切实感受处罚之痛，引以为戒。

4 数值仿真与分析

本节对基于空间复用的机会频谱接入运用学习算法SLA［12］进行数值仿真。基本仿真参数参考文献［8］设置如下:认知用户个数N=9，信道个数M=3(干扰图如图2 所示，其中每个圆表示一个认知无线链路，虚线表示在认知用户之间存在干扰)，SLA 算法步长b=0.05。仿真结果如图3～6 所示。

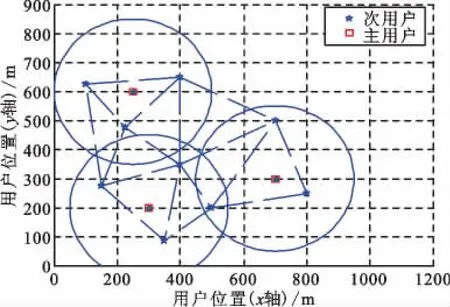
图2 干扰图Fig.2 Interference graph

由图3 可以看出，随着迭代次数的增加，非对称信道总干扰(势能函数的负值)和对称信道总干扰［8］都在逐渐减小，这是因为由于空间复用在每次迭代中每个用户及其相邻用户之间相互博弈，最终使系统效用函数最大化即总干扰最小化，也就是说纳什均衡解即是全局最优解。非对称信道速率总干扰和对称信道速率总干扰分别在迭代次数接近250次和400 次时收敛于零，并达到稳定即纳什均衡，可见改进后总干扰比文献［8］收敛速度快。这是因为在非对称信道速率即不同信道条件的约束下，很显然会使可行解范围变小，从而使收敛速度变快且使系统性能不会减弱。

图3 总干扰对比Fig.3 Comparison of the total interference

图4 说明了随着迭代次数的增加，信道选择概率矢量由{1/3，1/3，1/3}在迭代次数为350 次时最终变成了{1，0，0}，换句话说，认知用户1 最终会选择信道2 进行传输，即验证了该博弈模型的收敛性。

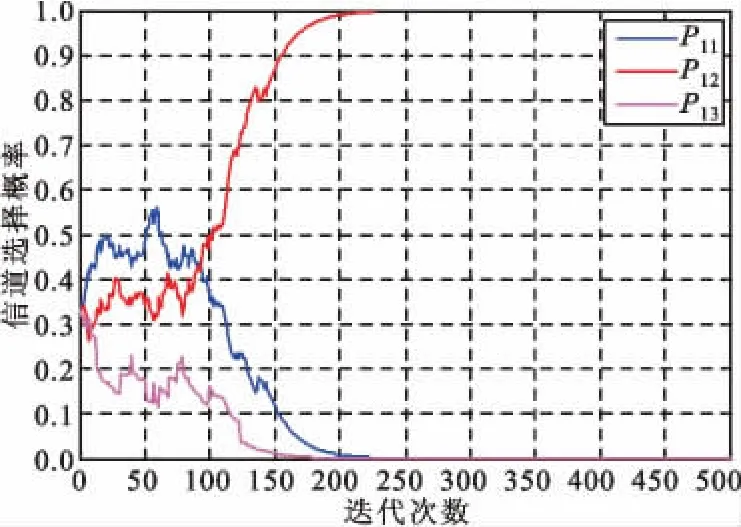
图4 信道选择概率和迭代次数的关系Fig.4 The relationship between channel selection probability and the iterative times

图5 表明非对称信道的谱效(系统吞吐量与总带宽的比值)比对称信道的谱效有很大提高，随着信道空闲概率的增大，系统谱效也逐渐增大。这同时也说明了非对称信道因素能很大程度地提高机会频谱接入的谱效性能，从而提高频谱利用率。

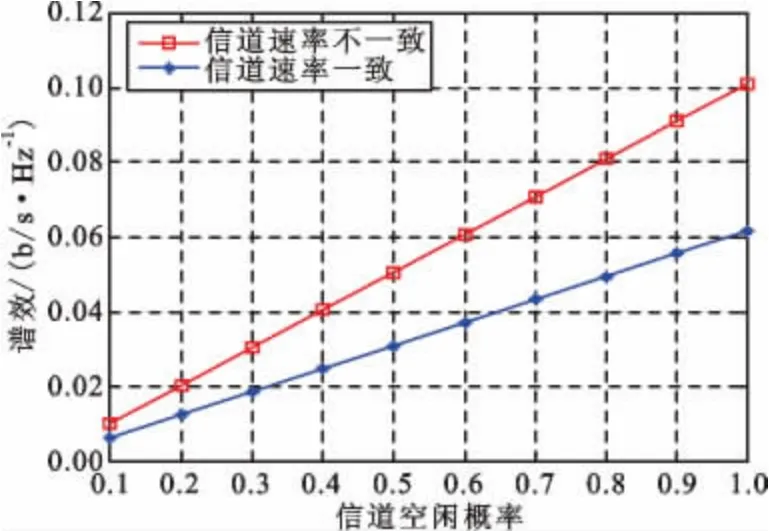
图5 谱效对比Fig.5 Comparison of spectral efficiency

在图6 中为了进行统一标准的比较，假设Ran=1。从图中可以看出，基于空间复用的系统吞吐量比传统系统吞吐量有很大的提高。这是因为考虑到用户位置的差异性，如果用户位置足够远，它们可以在同一频带传输，很显然就会使系统吞吐量有很大的提高，借此提高频谱利用率。

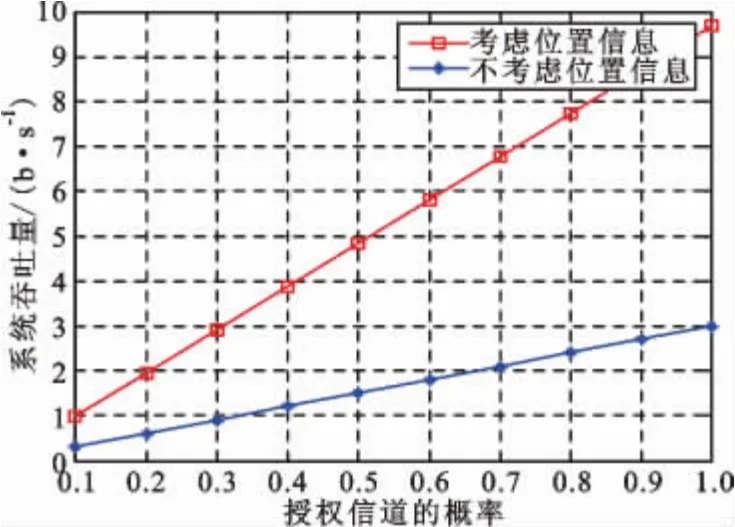
图6 系统吞吐量对比Fig.6 Comparison of system throughput

5 结束语

本文借助认知用户空间位置分布干扰图评估用户间干扰，并基于此研究了空间复用的动态频谱接入优化问题;构建了基于空间复用的系统吞吐量优化模型，通过最优信道选择集合的确定，最大化系统吞吐量;提出了吞吐量倒数的负值最大化的博弈模型，使该博弈是至少具有一个纯策略纳什均衡的势能博弈且纳什均衡点是上述优化问题的全局最优解。仿真结果证明了优化问题的合理性和有效性，并表明考虑空间位置信息时，可进一步提高认知网络的机会接入吞吐量和谱效。但以下问题有待进一步研究:认知用户在空间位置上的移动性对系统性能及最优信道集选择的影响;用户业务需求不同(电话、短信等)和Qos 要求不同对系统吞吐量的影响。

［1］嵇建波，葛仁华.伺机频谱接入协同分集的中断概率［J］.电讯技术，2009，49(9):7－10.JI Jianbo，GE Renhua.Outage Probability of Cooperative Diversity with Opportunistic Spectrum Access［J］.Telecommunication Engineering，2009，49 (9):7－10.(in Chinese)

［2］Shuminoski T，Janevski T.Radio network aggregation for 5G mobile terminals in heterogeneous wireless networks［C］//Proceedings of 2013 11th International Conference on Telecommunication in Modern Satellite，Cable and Broadcasting Services.Nis:IEEE，2013:225－228.

［3］Ning Z L，Song Q Y，Guo L，et al.Throughput improvement by network coding and spatial reuse in wireless mesh networks［C］//Proceedings of 2013 Global Communications Conference.Atlanta，GA:IEEE，2013:4572－4577.

［4］Fudenberg D，Tirole J.Game Theory［M］.Cambridge，MA:MIT Press，1991.

［5］Felegyhazi M，Cagalj M，Hubaux J P.Efficient MAC in Cognitive Radio Systems:A Game－ Theoretic Approach［J］.IEEE Transactions on Wireless Communications，2009，8(4):1984－1995.

［6］Niyato D，Hossain E.Competitive Spectrum Sharing in Cognitive Radio Networks:A Dynamic Game Approach［J］.IEEE Transactions on Wireless Communications，2008，7(7):2651－2660.

［7］Xu Y H，Wang J L，Wu Q H，et al.Opportunistic Spectrum Access in Unknown Dynamic Environment:A Game－Theoretic Stochastic Learning Solution［J］.IEEE Transactions on Wireless Communications，2012，11(4):1380－1391.

［8］Xu Y H，Wu Q H，Shen L，et al.Opportunistic Spectrum Access With Spatial Reuse:Graphical Game and Uncoupled Learning Solutions［J］.IEEE Transactions on Wireless Communications，2013，12(10):4814－4826.

［9］Chen Xu，Huang J W.Distributed Spectrum Access with Spatial Reuse ［J］.IEEE Journal on Selected Areas in Communications，2013，31(3):593－603.

［10］Arnborg S.Efficient Algorithms for Combinatorial Problems on Graphs with Bounded decomposability—A Survey［J］.BIT Numerical Mathematics，1985，25(1):1－23.

［11］He J.An hybrid heuristic algorithm for the Two－Echelon Vehicle Routing Problem［C］//Proceedings of 2012 IET International Conference on Information Science and Control Engineering.Shenzhen:IET，2012:1－5.

［12］Sastry P，Phansalkar V，Thathachar M.Decentralized Learning of Nash Equilibria in Multi－Person Stochastic Games with Incomplete Information［J］.IEEE Transactions on Systems Man and Cybernetics，1994，24(5):769－777.