改进的极化SAR 点散射目标扰动滤波检测方法*
孙 盛,徐志佳,刘仁峰
(1.广东工业大学 计算机学院,广州 510006;2.贵阳学院 机械工程学院,贵阳 550005;3.华中科技大学 电子信息与通信学院,武汉 430074)
1 引言
极化合成孔径雷达(Polarimetric Synthetic Aperture Radar,PolSAR)图像中存在较多的点散射目标。点散射目标一般都对应着比较重要的目标,比如城市场景中的建筑物、车辆、金属物体等。为了准确地对这些目标进行分类、识别,有必要设计出识别率更高的检测器。传统方法更多的是利用PolSAR 图像数据的统计信息进行检测,而利用成像数据本身的物理信息完成检测的方法往往被忽视,因此,本文正是从这一思路出发,拟以成像数据本身的物理信息为重要依据,完成点散射目标的检测。
点散射目标的检测一般有三大类方法。第一类方法是基于统计数据的方法,如Novak 提出的最优极化检测方法(Optimal Polarimetric Detector,OPD)[1]。该方法以PolSAR 图像的散射矩阵为研究对象,通过极化匹配滤波器完成点散射目标的检测,但是,该检测方法是基于目标和背景噪声的先验信息的,因此,在未知这些先验信息的情况下,该方法是无法实施的。第二类方法是基于物理信息的,此类方法一般假设点散射目标大多数是由人造物体所散射的回波,这类物体的散射回波能量较强。但是,此类方法很容易受到噪声的影响,特别是具有较强幅度的相干斑噪声。因为该类检测器一般都是通过计算单一通道的幅值(例如共极化通道或者交叉极化通道)来判定的。这类方法的优点在于计算方式简单,而缺点是漏检率和虚警率较高。该类方法中有代表性的方法有Improved Sigma 方法[2-3]。Improved Sigma 方法的基本原理是首先计算整幅图像中的交叉极化通道的能量值的98%分位数,如果某个像素点的交叉极化通道能量大于此分位数,则认为是点散射目标。此外,也有一些基于此原理的改进方法,如能量最大合成法(Power Maximization Synthesis,PMS)[4]。PMS 方法是通过计算4个全极化通道的总功率来判定的,该方法对于自然目标的判定仍然具有较高的漏检率和虚警率。第三类方法被称为极化白化滤波(Polarimetric Whitening Filter,PWF),虽然其名称为滤波,但其主要功能是完成点散射目标的检测。该方法采用了统计信号处理的原理,并且不需要任何的先验信息,是一种性能优异的经典方法[5-6]。近年来,有学者提出了一种新的检测模型,该模型被称为几何扰动滤波模型[7-9]。该模型在仿真数据、真实数据上得到了性能上的验证,目前来看,其效果优于极化白化滤波。但是,该模型在应用过程中还存在一定问题,主要有相干度参数阈值无法根据场景数据分布自适应获取和不同散射机制的检测共用单一阈值,本文正是要针对这两个问题,设计一种改进的检测算法。
2 扰动滤波检测器的基本原理
2.1 散射机制的表达方式
散射矩阵一般用于描述雷达的入射电磁波和散射电磁波之间的关系,在效果上它表达了观测对象的物理、几何等属性,是研究观测对象的最重要的数据形式之一。因表达电磁波时必须指明天线的极化状态,所以散射矩阵的形式也依赖于天线的极化状态。一般情况下,天线的极化状态为水平极化线性极化、垂直极化线性极化,分别用字符H 和V 表示,有时也把两种极化对称为笛卡尔极化基。为了便于运算,通常会把散射矩阵元素展开为一个列向量的形式,称之为目标向量。散射矩阵的形式参见公式(1),目标向量的形式参见公式(2)。值得注意的是,在表达目标向量的时候,还需要指定一个矩阵基底,在此采用的是线性基底;矩阵中的每一个元素S代表的是复散射系数;本文讨论的都是单基地雷达,散射矩阵满足互易定理,有SHV=SVH;为了便于计算,可将散射目标向量规范化,用符号Ω 表示[10]。
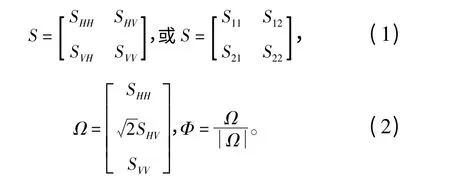
引入目标向量之后,自然界中的很多经典散射机制都可以唯一地用目标向量来表达,如二面角散射、偶极子、三面角散射等。但是,因众多复杂因素的影响,合成孔径雷达的观测对象一般均不属于严格意义上的单一散射机制。例如,因发射电磁波的波长的影响,单个像素单元内部可能包含多种散射机制;相干式采集信号的过程中,由于物体的变化(例如树叶受到风力吹动)而产生的随机性,这些具有随机性的散射目标被称为分布式散射目标。而经典散射机制对应的散射目标都是点散射目标,它们具有单一、稳定的散射属性。正因如此,合成孔径雷达的观测数据可被视作是一个随机过程。为了描述这个随机过程的特征,必须引入二阶统计量,即协方差矩阵或相干矩阵来表达。不失一般性,以协方差矩阵作为研究对象,其定义参见公式(3):
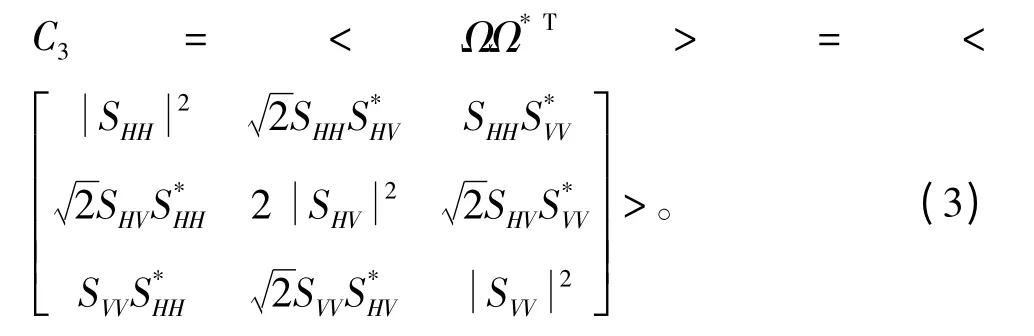
值得注意的是,公式(3)中的运算符号<… >表示的是统计平均运算。根据合成孔径雷达系统采集数据的方式可知,无法用时间来代替统计平均,一般只能用空间域的数据平均来代替统计平均。
2.2 几何扰动滤波检测器的内在机理
为描述两种散射机制的相似性,首先引入极化相干度参数,其定义参见公式(4):
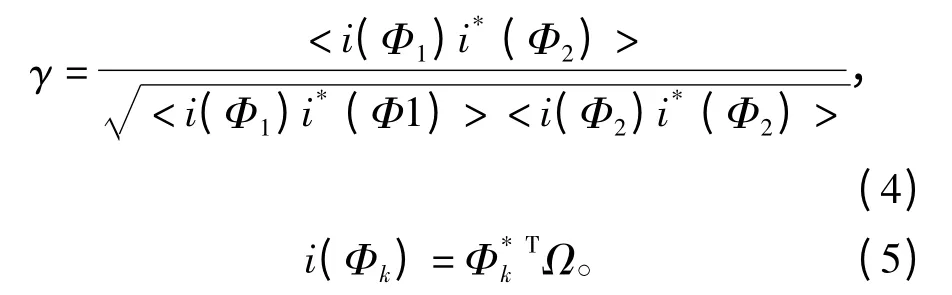
式中,i(Φk)为某像素的散射向量在某种散射机制上的投影。极化相干度参数γ 是一个复数。
为了获得一个经过“微小扰动”滤波的散射机制,还需要引入Huynen 变换。简单而言,对某一散射机制进行Huynen 变换,就可以得到该散射机制对应的9个Huynen 参数。将这9个参数中的某一个进行微小的变化,得到一组新的Huynen 参数,这组参数对应一个经过“微小扰动”的新散射机制,这就是所谓的几何扰动滤波[6-7]。经过“微小扰动”得到的新散射机制在物理上是与原散射机制非常接近的。
对于点散射目标的检测,基本原理如下:选取某个待检测的像素点X,将像素点X 的邻近N ×N 窗口内的像素参与运算。在经典散射机制库中挑选一个点散射机制ΦT,经过“微小扰动”滤波后,得到一个相近的点散射机制ΦP。在点X 的邻近N ×N 窗口内,ΦT和ΦP的相干度参数为γ。如果γ 的模较高(接近于1),可认为像素点X 属于点散射机制ΦT;否则,可认为像素点X 属于分布式散射目标[9]。
3 改进的扰动滤波检测器
3.1 经典算法存在问题的分析
对于点散射目标的检测,经典算法是通过极化相干度参数的模来判断的,预先设定的阈值T 为0.98,当γ≥T 时,认为该像素是属于点散射目标的一种。这种阈值的设定方法显然是无法适应场景的变化的,因此需加以改进。假设有一幅PolSAR 图像,在其场景中添加一些噪声,那么计算得到的极化相干度参数的分布肯定会发生变化,而阈值仍然保持为0.98,这会导致检测出点散射像素的数量发生变化。由此可知,阈值的设定必须根据场景来自适应的调整,而且,为了实现全自动化的检测,阈值的调整不能有人为智力因素的介入。
3.2 改进的几何扰动滤波检测方案
在此,本文提出利用Cloude-Pottier 分解的改进方法完成阈值的自动获取。基本原理如下:对PolSAR 图像实施Cloude-Pottier 分解,得到每一个像素点的熵参数(Entropy,简记为H)和平均阿尔法角参数(Averaged alpha angle,简记为 珔α);熵参数表征了散射单元内部每一种散射类型的统计无序性,熵参数的定义是基于特征值的,与具体的矩阵基底的形式无关,这就可以保证本方法可以适用于不同的矩阵基底形式;平均阿尔法角参数 珔α 表达了对散射机制的一种粗分类。
第一,已经有学者通过大量实验证明,当熵参数H 比较低的时候,一般认为当H <0.3 时,对应的像素单元被认为是高度极化,此时像素单元被认为是一种确定性的点散射体。而且,熵参数的计算是采用邻域加权平均的方式完成的,受到噪声的影响会减弱。具体实现时,可首先将PolSAR 图像实施Cloude-Pottier 分解,统计出H <0.3 的像素点的数量,然后用这个数值除以PolSAR 图像总像素点数量即得到一个比例因子R%。最后,针对某一种经典散射机制,再对PolSAR 图像所有的像素点计算出极化相干度参数,对这些相干度参数排序,按比例因子R%取前列的像素点,最低像素点对应的极化相干度参数即取为阈值[10-11]。
第二,经典算法中对于所有散射机制都是共用单一阈值,这显然也是不合理的。Cloude- Pottier分解平均阿尔法角是像素单元内的多种散射机制的一种加权平均值,虽然不能很精确地表征像素的散射机制,但是能够作为一种初分类的输入值。因此,对于某种散射机制,可以缩小其统计范围,根据平均阿尔法角初分类的结果统计出比例因子R%,这样就可获取针对某种散射机制的阈值。
综合上述两点,可得到改进的算法的实现流程,如图1 所示。
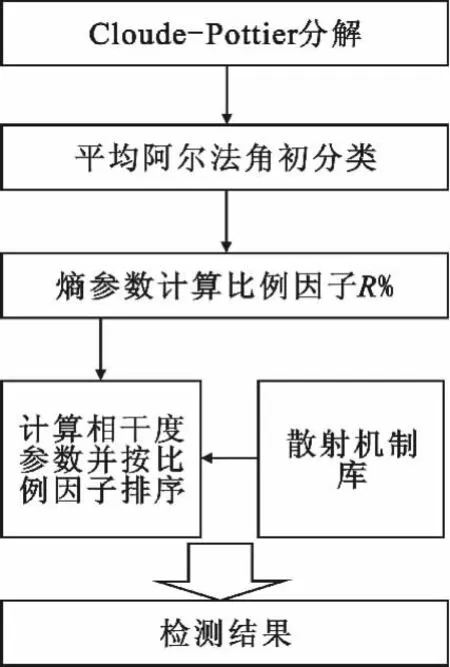
图1 改进的几何扰动滤波检测算法流程图Fig.1 Flowchart of the improved geometrical perturbation filter based detector
4 实验及分析
4.1 实验数据及实验方案
为了验证改进方法的有效性,选用了机载合成孔径雷达(AIRSAR)成像系统的数据,样本图像选取的是San Francisco Bay,极化方式为全极化,其余主要参数参见表1。

表1 San Francisco Bay 极化图像主要参数Table 1 The main parameters of sample PolSAR data named San Francisco Bay
首先,构建散射机制库,包含了6 种散射机制,分别为奇数次散射Odd、水平偶极子Hdipole、有朝向偶极子OriDipole、二面角Dihedral、右手螺旋RHelix、左手螺旋LHelix。6 种散射机制对应的颜色分配图参见图2,其中,01 黑色对应的是分布式散射机制,02 绿色对应的是奇数次散射Odd,以此类推。
图2 6 种散射机制对应的颜色分配图Fig.2 The color configuration of six scattering mechanisms
其次,可以适当对样本图像San Francisco Bay实施相干斑噪声的滤波,在此采用Lee Sigma 滤波;然后,实施Cloude- Pottier 分解,得到平均阿尔法角、熵参数。根据平均阿尔法角完成所有像素点的初步分类,然后根据熵参数的统计分布得到比例因子R%。依次从散射机制库中挑选出散射机制,利用协方差矩阵数据计算得出极化相干度系数。根据比例因子R%进行排序,由排序结果得到该类散射机制对应的阈值。
4.2 实验结果及分析
按照设定的实验方案,将San Francisco Bay 的原始Pauli 图像、采用经典方法的检测结果(未滤波)、采用经典方法的检测结果(Sigma 滤波)、采用改进方法的检测结果(Sigma 滤波)进行对比。从图3 中的4 幅子图可以看出,(b)中的结果是在未滤波时得到的,因相干斑噪声的影响,会使得大多数像素点的极化相干度系数偏大很多,特别是在海面出现了很多斑点;(c)中的结果是在实施Lee Sigma 滤波之后得到的,因相干斑得到了抑制,因而极化相干度系数变小,但因阈值设定的不合理(偏高),很多散射机制点没有检测出来;(d)中的结果是采用改进方法得到的检测结果(实施Sigma 滤波后),因新的方法根据每种散射机制的分布情况和整幅图像的数据分布情况自动获取的阈值,因而,检测结果更加合理,因雷达照射角度的影响,大多数海面上基本上没有回波。另外,图像右上部出现了二面角散射,这也是因照射角度的影响。同时,在桥面也检测出了单次散射和少量的二面角散射,这是因为桥面比较平整、桥体与水面形成二次散射的缘故。

图3 点散射机制检测结果对比(Pauli 编码:R=SHH-SVV,G=2SHV,B=SHH+SVV)Fig.3 Comparison of detecting efficiency between the classical method and new proposed method(Pauli coding:R=SHH-SVV,G=2SHV,B=SHH+SVV)
为了验证检测结果的正确性,先将整幅图像的熵参数直方图绘制在图4(a)中,同时在检测结果中选取了两个海面区域和一个桥面区域,将它们的熵参数直方图分别绘制在图4 的(b)、(c)、(d)中。可以看出,检测结果对应的区域的熵参数都是小于0.3的,对应的是点散射机制。
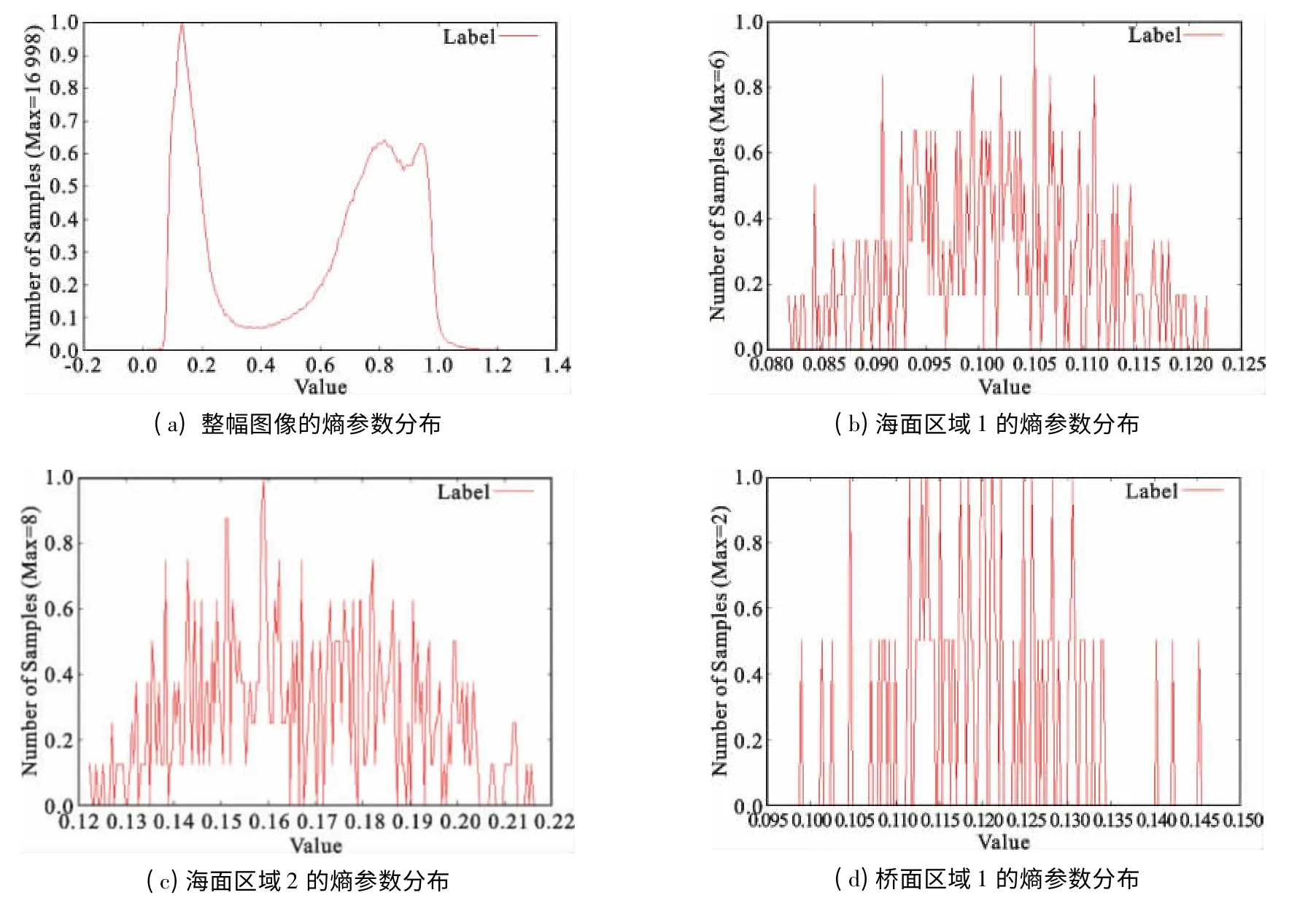
图4 熵参数的全局和局部结果对比Fig.4 Comparison of entropy profiles between the global area and local area
本文提出的算法对于机载平台、星载平台下的P、L、C 频段均是适用的,对分辨率为米级的多幅图像均进行了测试,算法的执行效果较好,限于篇幅在此就不一一列出了。
5 结束语
本文针对极化SAR 图像中的点散射检测问题,分析了经典方法中的阈值参数无法自动获取的缺陷,并结合极化非相干分解方法——Cloude-Pottier分解方法,对经典的扰动滤波检测器进行了改进。最后,对真实数据进行了定量的实验验证,实验结果表明,新的方法能够更好地完成点散射目标像素检测的任务。文中的结果可以作为PolSAR 图像非监督分类输入值,使得该分类方法可以更好地利用成像数据本身的物理信息。在后续研究中,可以结合野外实验对散射机制库的建立进行更加深入的研究,以此进一步提高检测准确率。
[1]Novak L M,Sechtin M B,Cardullo M J.Studies of target detection algorithms that use polarimetric radar data[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(2):150-165.
[2]Lee J S,Ainsworth T L,Wang Y T,et al.Polarimetric SAR Speckle Filtering and the Extended Sigma Filter[J].IEEE Transactions on Geoscience and Remote Sensing,2014,53(3):1150-1160.
[3]Lee J S,Wen J H,Ainsworth T L,et al.Improved Sigma Filter for Speckle Filtering of SAR Imagery [J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(1):202-213.
[4]Boerner W M,Kostinski A.On the concept of the polarimetric matched filter in high resolution radar imaging[C]// Proceedings of 1988 International Symposium on Antennas and Propagation Society.Syracuse,Italy:IEEE,1988:533-536.
[5]Novak L M,Burl M C,Irving W W.Optimal polarimetric processing for enhanced target detection [J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(1):234-244.
[6]张伟,王莉,耿健,等.基于Pauli 基展开的联合极化SAR微多普勒分析[J].电讯技术,2014,54(4):446-451.ZHANG Wei,WANG Li,GENG Jian,et al.Analysis of micro- Doppler combined with polarimetric SAR based on Pauli-basis expansion[J].Telecommunication Engineering,2014,54(4):446-451.(in Chinese)
[7]Marino A,Cloude S R,Woodhouse I H.A Polarimetric Target Detector Using the Huynen Fork [J].IEEE Transactions on Geoscience and Remote Sensing,2010,48(5):2357-2366.
[8]Marino A,Cloude H I,Woodhouse I H.Statistical Tests for a Ship Detector Based on the Polarimetric Notch Filter[J].IEEE Transactions on Geoscience and Remote Sensing,2015,53(8):4578-4595.
[9]Marino A,Cloude S,Sanchez-Lopez J M.A New Polarimetric Change Detector in Radar Imagery [J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(5):2986-3000.
[10]Jin Y Q,Xu F.Polarimetric Scattering and SAR Information Retrieval [M].New York:John Wiley & Sons Inc.,2013.
[11]Ma J Y,Qiu W C,Zhao J,et al.Yuille,and Zhuowen Tu.Robust L2E Estimation of Transformation for Non-Rigid Registration [J].IEEE Transactions on Signal Processing,2015,63(5):1115-1129.

