态函数熵的意义及应用研究

邵琪珺

（无锡职业技术学院 基础课部，江苏 无锡 214121）

熵的概念已经无处不在，它渗透到生物学、环境学、社会学、经济学等各个领域。熵增会使能量弥散，能量退降，使世界向无序和混乱发展；而熵减可以使自然和社会的事物向有序的方向发展。熵不仅联系着旧事物的消亡，也与新事物的萌生有关。熵理论及应用已经成为人与自然和谐共处的新的世界观。

1 态函数熵

设热力学系统由平衡态1过渡到平衡态2，则初终状态的态函数有

式中，dQ表示系统在其间一个无限小可逆过程中（温度为T）所吸收的热量，S2和S1分别表示系统在状态2和状态1的熵。

如系统经无限小的可逆过程，则

熵的单位是J/K。

根据卡诺定理，克劳修斯还证明了对任意孤立系统的不可逆过程，有

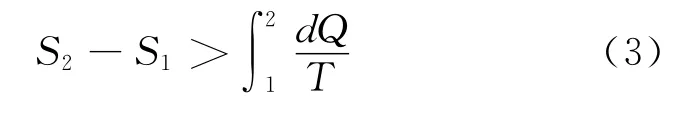
综合式（1）和（3）得出

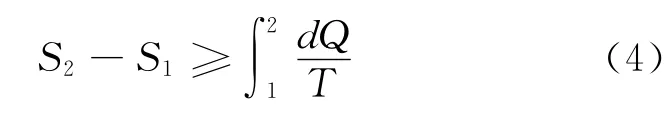
其中等号对应于可逆过程，不等号对应于不可逆过程。显然，对于孤立系统而言，它不从外界吸收热量，则

式（5）为熵增原理——孤立系统的可逆过程，其熵不变；孤立系统的不可逆过程，其熵增加。孤立系统内部自发进行的过程必然是一个不可逆过程，导致熵增。当孤立系统达到平衡态时，熵达到最大值，因此平衡态是孤立系统在一定条件下熵值最大的状态。用熵增原理可判断过程进行的方向和程度［1－2］。

2 三种熵及相互关系

前文提出的克劳修斯熵又称热力学熵。玻尔兹曼认为，系统的无序度可用系统的微观状态数w（或称热力学概率）来表述，认为：S∝lnW。普朗克引进了比例系数k（玻尔兹曼常数），得出玻尔兹曼关系式：

式（6）中的熵称为玻尔兹曼熵或统计熵。玻尔兹曼熵是从统计意义上说明自然界一切自发进行的过程都是从小概率状态向大概率状态发展的，平衡态的热力学概率最大。玻尔兹曼熵揭示了宏观态与微观态的联系，指明了热力学第二定律的统计本质。

熵是状态函数，克劳修斯熵只对平衡态有意义，它是系统平衡状态的函数，熵的变化量是指系统初、终平衡态之间的熵变。而玻尔兹曼熵对系统任意宏观态（包括非平衡态）均有意义，因为即使是非平衡态也有与之对应的热力学概率。由于平衡态熵值最大，因此可以说克劳修斯熵是玻尔兹曼熵的最大值。玻尔兹曼熵具有更普遍的意义。

仙农引入了信源的信息熵，后由詹尼斯将信息熵引入统计力学。

式（7）中的熵称为信息熵或广义熵。Pi表示系统的第i个微观态出现的概率。熵概念的这一推广，为熵从热力学进入信息、生物、经济等领域铺平了道路［2］。

李鹤龄认为：三种熵按定义出现有先后，克劳修斯熵最早，玻尔兹曼熵次之，信息熵最晚，但信息熵玻尔兹曼熵克劳修斯熵［3］。

若不确定事件的每个可能结果出现的概率相同，即P1＝P2＝…＝Pi＝P，P表示任意可能结果出现的概率，W 表示可能出现的结果总数，且则式（7）退化为

可见能从信息熵推导出玻尔兹曼熵。同样李鹤龄也验证了能从玻尔兹曼熵推出克劳修斯熵，从信息熵能推导出克劳修斯熵。

信息熵中的Pi可以是任何一种研究对象的概率，没有受到平衡态、热力学系统等的限制，与热量、能量的转换无关，可以使用到信息、生物、经济等领域，范围最广；玻尔兹曼熵具有克劳修斯熵的所有特征，也能延展到非热力学系统和远离平衡态的热力学系统的非平衡态，但受到等概率的条件限制；克劳修斯熵是玻尔兹曼熵的最大值，是宏观的热力学理论中的态函数，不可能推导出微观的玻尔兹曼熵。综上得出信息熵包含的内容最广，玻尔兹曼熵比克劳修斯熵概念广泛，即信息熵玻尔兹曼熵克劳修斯熵。

3 熵与能量品质

从热力学第一定律看，能量不会减少，但从热力学第二定律来看，随着实际过程的进行，能量总在退化。能量品质有高有低，品质高的能量可做功或供热，可以转为机械能、电能等供人类使用，而高品质的能量被耗散时，会被降级为较低品质的内能。不可逆过程在能量利用上的后果总是使一定的能量从能做功的高品质能转变为不能做功的低品质能，形成所谓“退降”的能量。

下面以理想气体的绝热自由膨胀为例，说明退降的能量Ed与系统的熵的增加成正比［2］。

设有物质的量νmol、温度为T、体积为V1的理想气体，与温度为T的热库接触做等温膨胀，体积变为V2时，从热库吸收热量Q，并使之全部转化为功Ai，则

如果气体是通过绝热自由膨胀使体积变为V2，则在膨胀过程中它不对外做功，热库内相应的这一部分能量也就不可能借助于气体对外做功加以利用了。要利用这部分的能量做功，只能借助于温度为T0的热库并使用卡诺热机，此时能得到的功是

这样由于气体自由膨胀而退降的能量是

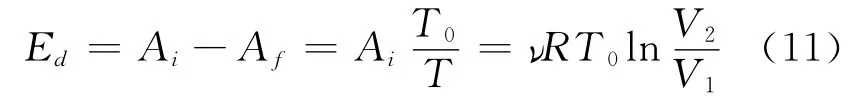
又因为理想气体绝热自由膨胀的过程不可逆，初终两态温度为T不变，气体熵的增量为

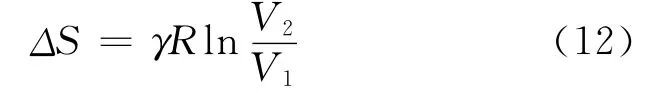
比较式（11）和式（12）可得

式（13）说明退降的能量与系统的熵增成正比。自然界所有的实际过程都是不可逆的，使得能量不断转变为不能做功的形式。提高热机的效率是提高能量品质的一种有效手段，但较难。节能和开发新能源是人类社会的重要课题。

4 熵与自然演化

克劳修斯的所谓“宇宙热寂说”与达尔文的进化论看似矛盾，实则不对立。热力学第二定律所揭示的“退化”是在与周围环境隔绝的密闭系统，而达尔文的生物进化系统则是一个时刻同外界环境进行物质、能量、信息交换的开放系统。根据普利高津方程

式中diS为系统内部自发产生的熵值，该项恒大于零；deS为系统从环境引入的熵流，即物质流、能量流、信息流。系统要想朝有序方向进化，就必须从环境中引入负熵流。只有当负熵流大于系统内部自发产生的熵增时，即｜deS｜＞｜diS｜时dS＜0，才能使系统朝熵减有序的方向进化。也就是说系统的进化是以环境中某些方面的退化为代价的。

比如，人类社会要生存和发展，就要不断地从自然界吸取负熵，尽可能向自然界索取各种可利用的矿产资源、森林资源、水利资源、动植物资源、空气资源等，人类社会也是依赖负熵维持的，同时又把各种工业垃圾、生活垃圾、有毒有害的气体和污染严重的废水排放到自然环境中。如果人类无节制地向自然索取和排放，那么，随着自然环境中正熵的积累越来越多，环境必然日益走向无序、退化。人类的进化不能以环境的退化为代价。必须协调好人与环境的矛盾，实现发展经济和保护环境的同步性［4］。

5 熵与经济和社会

经济系统是复杂系统，经济系统中存在物流、能流、货币流及相应的熵流。经济系统也是复杂的开放系统，它不断与自然界进行物质、能量、熵的交换。在物质交换中，输入物料资源、排除废物和产品。在能量交换中，输入可利用能，排除废物和废热。经济过程的生产、流通、消费环节都导致总熵增加。

有专家提出了经济能的概念。经济能是一种特殊的复合能量，它不仅具有各种类型的物理能和化学能，还具有在经济活动中做功的能力，即影响社会消费和社会经济的发展。类似于“能量退降”，在人类社会经济活动中，经济能也不能全部利用。即使科学技术再先进，经济能也不能全部转化为有效能，总有一部分转化为无效能，造成经济过程中的熵增［5］。生产过程中原料变成产品，产品部分熵减少了，但环境中的熵增加了（包括生产过程中废物和废热的排入）。工农业生产过程中形成的无法处理的废水，无法降解的白色污染，沙化的土地导致熵增；流通过程中各种交通工具产生的废气、扬尘导致熵增；消费过程中人体的新陈代谢，生活用品的升级换代，也必然带来环境污染和巨大的熵增。在生产中知识、技术等负熵流很重要，可以保证科学生产，减少能耗和废品。

要使经济社会不断发展，同时减少熵的产生，就要求人类能巧妙地掌握和利用自然规律，学习先进的科学技术。信息、知识和技术是负熵，能抵消生产和经济发展中的熵增，使社会有序发展。

在市场经济条件下，过量生产还会导致大量商品闲置，导致劳动力过剩，最终爆发经济危机，只有及时调节供求关系，调整产业结构，解决就业问题，才能化解经济危机。

6 熵与课堂教学

教学是复杂系统，由教和学两方面组成，教学活动中的各种联系如教师与学生，学生与学生，教师与教学内容，学生与教学内容，理论教学与实习教学等等组成了一个复杂的系统。教学又是一个开放的系统，不断与外界进行着物质、信息、能量的交换。教学系统在运行过程中熵会不断增大。比如学生在听课或实习期间能耗不断增加，精神会逐渐萎靡，注意力慢慢下降。从学期初的饱满状态到对所学课程内容逐渐失去兴趣，甚至无故缺课等。教学中需要引入负熵，使得教学向有序方向发展［6］。

教师先要针对不同个体的学生制定合理的教学方案，起点不能太高。课堂教学中应因材施教，尊重学生个性。教学也不能一味灌输，要提高学生的参与度，激发学生的学习兴趣。可采用小组讨论、动手制作等提高学生的教学参与度。要多培养学生的开放性思维，鼓励一题多解。教师还可变换教学节奏，有张有弛的完成教学任务。

开放是宏观有序的源头。只有输入负熵即增加鲜活的教学信息，通过生动的教学素材和多彩的教学形式来提高课堂教学质量，同时避免过多、过难的教学内容，才能确保教学系统总熵减少，使得教学向熵减有序的方向良性发展。

7 结语

“熵”这个源于热力学的概念已经渗透到人类生活的方方面面。不论是人的新陈代谢、植物的光合作用，还是清洁生产、环境保护和可持续发展，都能运用熵的理论来解决实际问题。熵理论还能运用到经济社会的发展中，保证科学生产，调整产业结构，节能减排，化解经济危机。

作为一名教师，应更多的思考熵理论在课堂教学中的合理应用，在开放的教学系统中，激发学生的思维，提高学生的学习兴趣，使教学良性发展。

［1］ 马文蔚，周雨青.物理学教程（上册）［M］.北京：高等教育出版社，2006.

［2］ 叶善专，张本袁，张玉萍，等.现代工程技术物理基础专题［M］.北京：清华大学出版社，2011.

［3］ 李鹤龄.信息熵、玻尔兹曼熵以及克劳修斯熵之间的关系——兼论玻尔兹曼熵和克劳修斯熵是否等价［J］.大学物理，2004（12）：37－40.

［4］ 钱兆华，李锐锋，高建明.自然辩证法教程［M］.武汉：湖北教育出版社，1999.

［5］ 王恒君.经济能·经济熵·经济危机［J］.数量经济技术经济研究，2002（2）：72－73.

［6］ 张进清，蒋士会.论教学的复杂性［J］.广西师范大学学报：哲学社会科学版，2010，46（2）：100－103.