地方高校绩效评估中的数学模型
地方高校绩效评估中的数学模型
赵高长1,高运芳2,覃飞3,王欣1,周彬1
(1.西安科技大学 理学院,陕西 西安 710054;2.西安工业大学 思政部,陕西 西安 710021;3.西安科技大学 教务处,陕西 西安 710054)
摘要:地方高校教学质量的准确评估,有助于高校之间取长补短,提高高校资源利用,引进良性竞争机制,最终实现学校整体教学水平的提高。通过对陕西省十多所地方高校广泛调研,对采集数据归类、合并,并作归一化处理,结合PCA,FCM,DEA及BMK算法提出了一种地方高校绩效评估中的数学新模型,给出了该模型的详细求解过程及算法流程,将该模型与传统模型进行了分析比较,基于FCM的优化选择算法将算法复杂度从O(2n-1)降到了O (n3),引进PCA的DEA模型与DEA-WEI模型复杂度相当。文中将网络上大学某知名排行榜的部分数据和搜集到的一些地方高校发展数据融合,经过优化整理,得到了备选标杆集的指标数据,然后利用论文所给模型借助MATLAB数学软件包在保守标杆集及积极标杆集两种情况下对这些高校作出评估,结果表明,方法简单实用、结论客观有效。论文将数据挖掘等数学方法有机融入到标杆分析中,用于地方高校绩效评估,探索出一条利用标杆分析提高高校教学管理的新思路,丰富了地方高校教学管理的理论和方法。
关键词:主成分分析;模糊C-均值算法;数据包络分析;标杆分析法;绩效评估
DOI:10.13800/j.cnki.xakjdxxb.2015.0222
文章编号:1672-9315(2015)02-0264-08
收稿日期:*2014-12-20责任编辑:李克永
基金项目:国家自然科学基金资助(41271518)
通讯作者:赵高长(1965-),男,陕西大荔人,教授,E-mail:zgc_xa1965@sina.com
中图分类号:G 47文献标志码: A
Mathematicalmodelofperformanceevaluationoflocalcollegesanduniversities
ZHAOGao-chang1,GAOYun-fang2,QIN Fei3,WANGXin1,ZHOUBin1
(1.College of Sciences,Xi’an University of Science and Technology,Xi’an 710054,China;
2.Teaching and Research Institute of Political Theory,Xi’an Technological University,Xi’an 710021,China;
3.Office of Teaching Affairs,Xi’an University of Science and Technology,Xi’an 710054,China)
Abstract:Accurate assessment of teaching quality of local universities can contribute to the complementarity among universities,the improvement of resource utilization,the introduction of healthy competition mechanism,and the enhancement of overall teaching level of universities.Through extensive research of dozens of colleges and universities in Shaanxi province,we classify,consolidate and normalize collected data,as well as combine PCA,FCM,DEA with BMK algorithm,in order to advance a mathematical model of performance evaluation of local colleges and universities,and to provide detailed solution procedure and algorithm flow of this model.Compared with traditional model,this new algorithm based on FCM reduces algorithm complexity from O(2n-1) to O(n3).The complexity of DEA model with PCA is equal to the complexity of DEA-WEI model.In this paper,we obtain the index data of the alternative benchmark after optimization of processing the combination of partial data from one well-known university ranking and collected data about development of local colleges.Then we utilize this model to assess universities with the help of MATLAB math package in two cases:conservative and positive benchmark sets,and the results are objective and effective.This paper organically integrates data mining and other mathematical methods into benchmarking analysis,which is applied to evaluate the performance of local colleges and universities,and explore a new idea to improve the teaching management of universities using benchmarking analysis,and to enrich the theory and method of local universities’ teaching management.
Key words:principal component analysis;fuzzy C-means algorithm;data envelopment analysis;benchmarking;performance evaluation
0引言
随着高等教育不断进步,招生规模不断扩大,教学资源相对不足引发的教学质量下滑问题日益凸显,高校在教学管理、学科建设和专业结构等方面越来越难以适应社会发展的需要[1]。面对这些难题,国外的经验就是学习或借鉴新的管理工具或方法,对自身做综合评价[2],明确优劣势,有针对性的进行改进,从而完善学校的管理制度和提高其竞争力。绩效评估是提高教学效益、并向社会展示其教育研究成果的主要手段。
准确和有效的对高校(定义为决策单元集,Decision Making Units,DMUs) 的绩效表现进行综合评价是一个数学问题。评估者常常需要评估多个绩效目标,这些绩效目标之间相互制约和冲突,如果只评价一个单一的绩效指标,评估者将很容易DMUs进行排序,但是那样做的后果会导致评估者忽略组织真正的绩效目标[3]。因此,高校的绩效评估从数学的角度来看就是一个典型的多目标决策问题。
运筹学领域的学者们先后研究出了很多理论和方法来解决这个问题,最为通用的有1947年由von Neumann和Mogenstem提出的期望效用函数理论(Expected Utility Theory,EUT);1954年由Savage提出的主观期望效用理论(Subjective Expected Utility Theory,SEUT)。此外,还有些其它的方法发展和应用,如Roy的ELECTRE法[4-5]、Brans等人的PROMETHEE法[6-8]、C.L.Hwang和K.Yoon的TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution)法[9]和Saaty,T.L的层次分析法(Analytic Hierarchy Process,AHP)[10-11]。通常人们认为AHP和TOPSIS代表了美国大学的研究,而ELECTRE和PROMETHEE则代表了欧洲大学的研究。
20世纪初泰勒在他的科学管理理论中引用标杆做为衡量工作绩效的一个有效标准,其后在全面质量管理(Total Quality Management,TQM)活动中应用标准数据来作为标杆以判断质量的符合性。始于20世纪90年代,标杆分析已成为目前国外高校研究中普遍使用的一种科学、系统、灵活的定量分析方法。最早在北美、英国和澳大利亚兴起,随后逐渐传播到欧洲各国。亚洲地区因接触得较晚,目前无论从理论还是实践都明显落后于欧美国家,香港大学是亚洲地区唯一参加到CHEMS CLUB活动中的大学。目前只有印度、韩国和香港地区的一些高校进行了标杆分析实践,中国内地还没有高校进行类似的活动。
在我国,高校应用标杆分析还是一个新课题,目前只有刘和旭等人将标杆分析法应用到了高校教师绩效评价方法的研究中,张大群等人则进行了标杆分析的数学理论及其应用研究,所用方法要么单一、要么缺乏量化分析。加之高校对提高高等教育质量和管理水平的重视程度还不够强,缺乏进行标杆分析研究和实施的专门人才,整体而言,尚处于学习阶段,值得高校进一步去研究和应用。
文中将结合模糊C-均值聚类(FCM)、主成分分析(PCA)[12]、数据包络分析(DEA)建立新的标杆分析(BMK)模型,以满足复杂情形下的高校管理分析需求。
1FCM和PCA相结合的标杆分析建模
标杆分析方法的有效性依赖于标杆集和指标集的合理选取,下文依据模糊C-均值聚类[13]数学方法进行科学选择。
1.1基于FCM的标杆集优化选择
假设在某生产实践中,给定待分析生产单元DMU0及属性b*和备选标杆集
pB={pb1,pb2,…,pbn},
其中pbi={pbi1,pbi2,…,bpiq}为第i个备选标杆及其属性。
为完成特定的标杆分析目的,需要获得合理的标杆集。这里的“合理”指所获得的标杆集应能为后续标杆分析的有效完成提供有力的支持。比如为制定近期发展目标,合理的标杆集中大部分标杆的生产效能应不能超出该生产单元太远,否则近期无法完成;而为制定长远发展目标,则大部分标杆的生产效能则应具有一定优势,否则无指导意义。因此,可以考虑需要解决如下优化问题

(1)
这里(bi-b*)+=max{bi-b*,0},(bi-b*)-=min(bi-b*,0);α为正实数,用于控制理想标杆集的状态;s为标杆集的最小规模;ΛB表示标杆集B中标杆的指标集。H(B,b*)的定义可根据实际需要进行调整。
显然这是一个NP难的问题,不容易求解。为此,引入数据挖掘中的模糊c-均值聚类算法[14],对备选标杆集进行划分,在划分结果基础上进行标杆集的优化选取。即建立如下优化问题
(2)
该模型是(1)的一种近似,其求解算法如下。

表1 标杆集优化选择算法
通过设置参数并执行上述算法,可以得到合理的标杆集B*,用于后续分析处理。
1.2PCA-DEA混合模型
确定合理的标杆集B*之后,需要对标杆集中各DMU和待评估的DMU0进行绩效评估,以正确认识优势和劣势,为后续生产效率的改善提供基础支持。
在现代生产实践活动中,经常涉及数量众多的指标[15],当指标数量过多时,不可避免的存在一些相互之间具有紧密联系的指标组,往往这些指标组在现实中反映为同一类型或者受相似因素影响,准确的获得指标之间的这些重要关联关系,能对绩效评估分析的有效完成提供有益的帮助。因此本部分拟结合PCA方法和DEA模型建立PCA-DEA混合模型用于标杆分析。
标杆集B*基础上具有平均偏好的DEA-WEI模型
(3)
考虑引进PCA模型对标杆集的属性集进行分析,并将结果用于DEA-WEI模型,即建立如下混合模型
(4)
同理,也可将PCA引入到具有矩阵偏好的DEA-WEI模型。
结合PCA计算过程可以给出上述混合模型的求解算法,见表2.

表2 PCA-DEA混合求解算法
2模型分析
本部分对上一节所建立模型及求解算法进行初步分析,为进一步的模型应用提供基础保障。
2.1标杆集优化选择算法分析
对于标杆集的选择问题来说,现有的研究基本上都是通过主观经验进行选择,少部分研究则是在一些简单的数据处理基础上结合主观经验进行选择。结合数据挖掘相关技术进行标杆集的优化选择方面的研究还少有人涉及。论文从最优化的角度出发,根据实际分析需求,建立了优化模型(1)。下面分析其求解算法的计算复杂度。
不妨设备选标杆集pB的规模为n,即含有n个备选标杆。记评价函数H(B,b*)计算一次为一个度量单位。由于B是pB的子集且规模大于等于s,则由组合原理得,B的选择数为
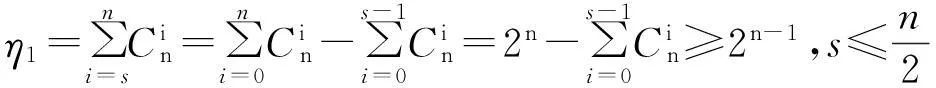

图1 模型(1)求解算法复杂度分析 Fig.1 Complexity analysis for model (1) algorithm
即当标杆集规模不超过备选标杆集的一半时,该模型求解算法的计算复杂度至少为O(2n-1),这在n较大时是相当可观的。Matlab编程得到复杂度曲线如图1所示。
模型(2)是模型(1)的近似,牺牲了目标标杆集的部分合理性以获得求解效率的提高。同样在上述假设下,记一次FCM的代价为δ,则可得



图2 标杆集优化选择算法复杂度分析 Fig.2 Complexity analysis for the benchmark set optimal selection algorithm

图3 PCA-DEA求解算法复杂度分析 Fig.3 Complexity analysis for PCA-DEA algorithm
2.2混合求解算法分析
对于DEA-WEI模型来说,并没有考虑DMU单元内各个指标间的相互关系及其对后续分析的影响[16]。通过数据挖掘技术进行指标集的成分分析,由此建立更简洁且具代表性的综合指标集并进行绩效评估分析等方面的研究还少有人涉及。论文以PCA和DEA为基础,建立了混合优化模型(4)。下面分析新模型和DEA-WEI模型求解算法的计算复杂度。
对于DEA-WEI模型(3)来说,实际上是关于k个变量的线性规划问题,如果采用单纯形法求解,通常具有多项式复杂度,最坏的情形下具有指数复杂度O(2k).如果采用内点法,则具有复杂度O(k3.5).

以内点法求解线性规划为例,则两个模型的复杂度曲线如图3所示。
综上,特定情形下,新模型的求解在复杂度上略有增加,但是能给出便于后续分析讨论的更丰富结果。这在某些实际应用场合,可以发挥更好的作用。
3实例分析
近年来,针对高校的评估活动和相关排行榜不断涌现,在不同程度上对各校发展状况做了一定的反映。为了更科学的评价各相关高校发展状况,为高校后续发展及教学管理水平的提高提供更好的帮助,本部分拟以一些典型的排行榜数据和调查数据为依据,进行标杆分析。
3.1指标集准备
本次标杆分析的备选标杆集设定为部分陕西省内高校(依次为西安电子科技大学、长安大学、西安科技大学、西安建筑科技大学、西安理工大学、西安交通大学、西安石油大学、西安工程大学、陕西科技大学、西安邮电大学),相关指标数据来源包括2013年武书连大学排行榜、各校发展报告和校情报告、网络搜集数据等。
综合各数据来源,归纳整理后,相关指标有16项分别以阿拉伯数字1~16表示(依次为研究生培养实力、本科生培养实力、自然科学研究实力、社会科学研究实力、培养的博硕士数、本专科生数、专任教师数、高级职称教师数、一级博士学科数、二级博士学科数、一级硕士学科数、二级硕士学科数、国家重点学科数、省部重点学科数、本科专业数、博士后科研流动站数),分别以字母A-J表示各备选标杆。为了后续处理方便,对每个指标数据进行归一化。最终得到见表3.
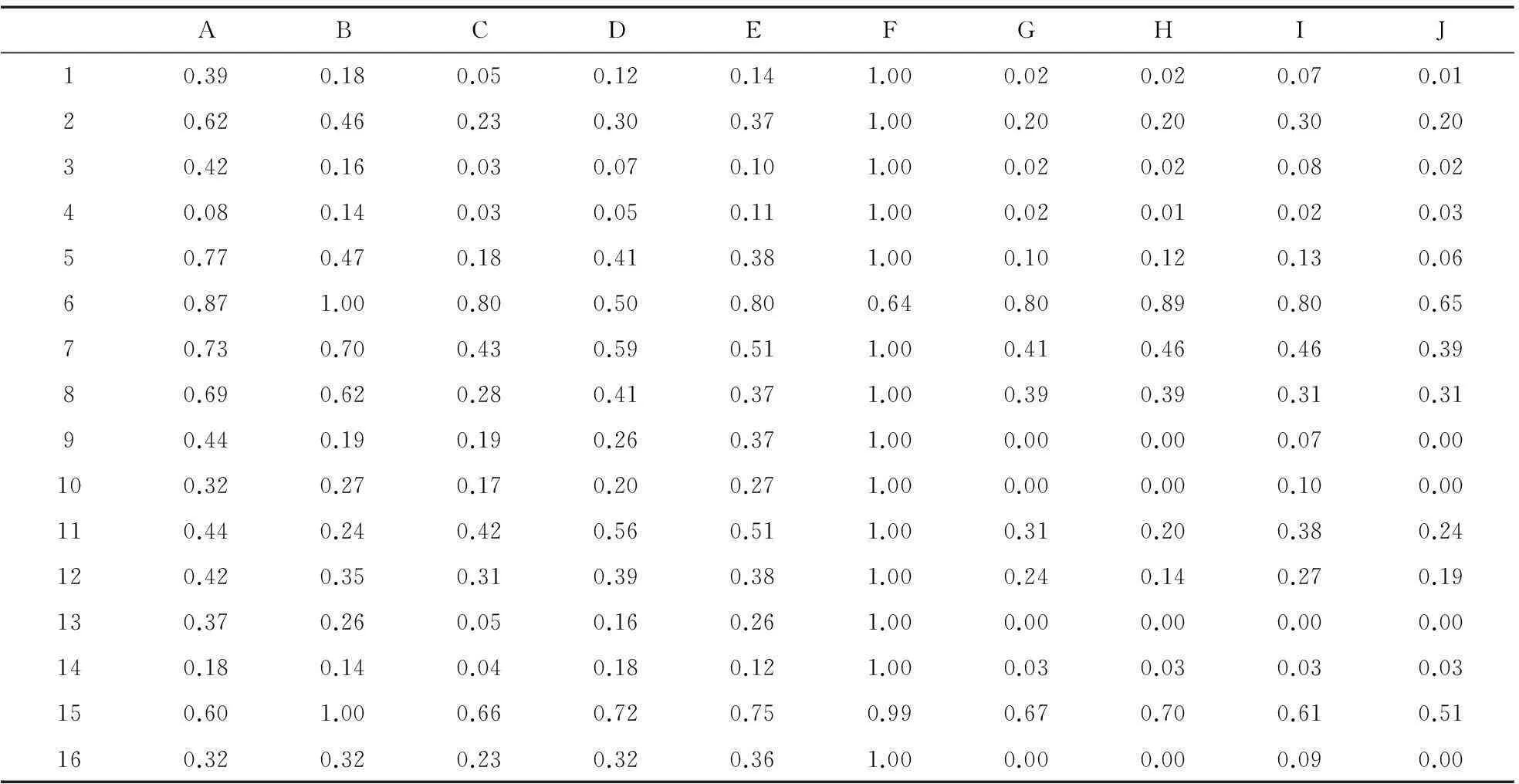
表3 归一化指标集数据
表3列出了我们搜集到的所有备选标杆的指标集数据,可根据实际应用需求对指标集进行选取并进行分析。
3.2模型应用及结果分析
针对所给数据,进行某DMU单元(不妨考虑C)综合实力的科学评估,为今后教学管理方向把握、政策制定提供一定的支持。按照第1节中所建立模型和算法,首先需要进行标杆集的选择,即应用基于FCM的标杆集优化选择模型(2)。
根据求解算法,得到表4.

表4 标杆集优化结果
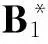
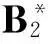
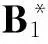

表5 积极标杆分析的DEA-WEI结果
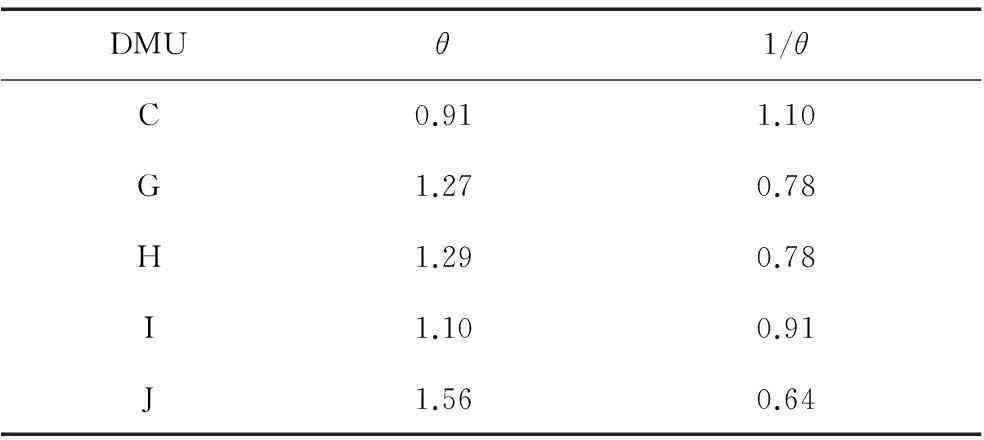
表6 实例1保守标杆分析的DEA-WEI结果
可见,待考核单元C略强于标杆G,H,I,J.这与实际情况具有一定的一致性。后续可以通过进一步分析确定优势环节,保持良好绩效。
当需要进行特定范围的评估分析时(比如对科研绩效进行评估),则可对指标集设置适当的权重,再通过模型求解。


表7 积极标杆分析的PCA-DEA结果
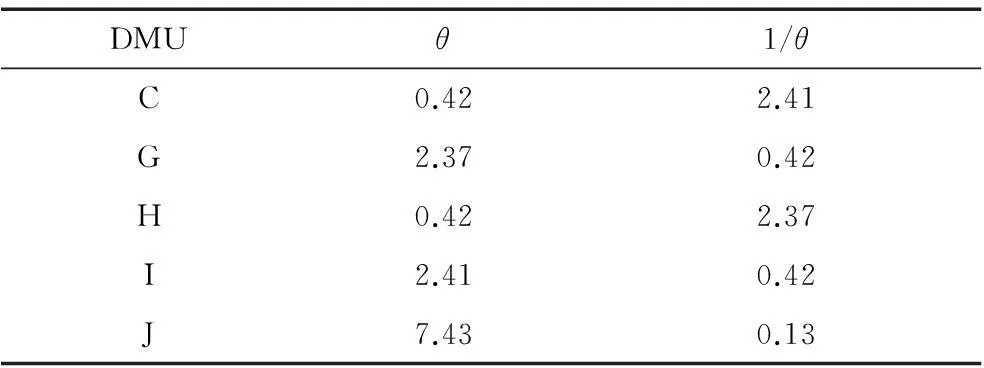
表8 保守标杆分析的PCA-DEA结果
待考核单元C仍在不同程度上弱于A,B,D,E,但值得注意的是标杆D的绩效反而超过了原来排在首位的标杆A,这说明在某些指标的组合结构上,D有比A更显著的特征,值得C比较学习。
待考核单元C在不同程度上优于G,H,I,J,但值得注意的是标杆H的绩效优于标杆I,这说明在某些指标的组合结构上,H有比I更显著的特征,值得C比较学习。
4结论
当前日益复杂的社会经济环境下,进行科学的绩效评估和分析显得尤为重要。标杆分析作为一种有效的绩效评估和管理手段,在各行业受到越来越广泛的应用,也产生了众多研究成果。众多高校经历了多年的高速发展,正处于发展转型期,进行科学的绩效评估和分析,能为长期发展提供有效的帮助。目前标杆分析在这方面的应用研究相对较少。
结合现代数据挖掘技术进行新标杆分析模型的研究具有一定的科学性和创新性,能为复杂绩效评估和分析提供一定的基础支持。鉴于此,论文首先结合模糊c-均值聚类、主成分分析、数据包络分析等对标杆分析模型进行了新的研究,建立了标杆集优化选择模型和PCA-DEA混合模型,并给出了求解算法。然后利用部分搜集的地方高校数据构建了标杆集指标数据,应用所建立模型进行了标杆分析。
研究结果表明:所建立模型结合了数据挖掘技术和标杆分析方法的特点,能满足一定的复杂绩效评估和分析需求,可为地方高校教学管理提供一定的数据支持。
参考文献References
[1] 冯晓光.土木工程专业大学生就业与专业实践的关系[J].西安科技大学学报,2012,32(5):667-670.
FENG Xiao-guang.On the relationship between obtaining employment and practice of civil engineering graduates[J].Journal of Xi’an University of Science and Technology,2012,32(5):667-670.
[2]许满贵,梁念兴,宝银昙.煤矿安全评价关键问题及对策[J].西安科技大学学报,2013,33(2):136-141.
XU Man-gui,LIANG Nian-xing,BAO Yin-tan.Key problems of coal mine safety evaluation and countermeasures[J].Journal of Xi’an University of Science and Technology,2013,33(2):136-141.
[3]Martin,B R.The use of multiple indicators in the ass-essment of basic research [J].Scientometrics,1996,36(3):343-362.
[4]Roy,B.The problems and methods with multiple objective functions[J].Mathematical Programming,1971,1(1):239-266.
[5]Roy B.Multicriteria methodology for decision Aiding[M].Dordrecht:Kluwer Academic Publishers,1996.
[6]胡君,蒋艳.PROMETHEE方法在城市环境空气质量评价中的应用[J].上海理工大学学报,2012,34(4):318-322.
HU Jun,JIANG Yan.PROMETHEE method applied in the evaluation of urban air environmental quality[J].Journal of University of Shanghai for Science and Technology,2012,34(4):318-322.
[7]Brans J P,Vincke P.A preference ranking organization method:the PROMETHEE method for MCDM[J].Management Science,1985,31(6):647-656.
[8]Braes J P,Mareschal B,Vincke P.How to select and how to rank projects:The PROMETHEE method[J].European Journal of Operation Research,1986,24(2):228-238.
[9]Hwang C L,Yoon K.Multiple attribute decision making[M].New York:Sgringer-Verlag,1981.
[10] Saaty T L.A scaling method for priorities in hierarchical structures[J].Journal of Mathematical Psychology,1977,15(3):234-281.
[11] Saaty T L.The analytic hierarchy process:planing,priority setting,resource allocation[M].New York:McGraw-Hill International Book company,1980.
[12] 张俭让,杨日丽.主成分分析法在煤矿通风系统评价中的应用[J].西安科技大学学报,2011,31(6):745-749.
ZHANG Jian-rang,YANG Ri-li.Application of principal components analysis to mine ventilation system evaluation[J].Journal of Xi’an University of Science and Technology,2011,31(6):745-749.
[13] 李洪,蒋金泉,张开智.回采巷道围岩分类的模糊聚类分析方法[J].西安科技大学学报,2005,25(1):12-16.
LI Hong,JIANG Jin-quan,ZHANG Kai-zhi.Fuzzy clustering analysis of tunnel surrounding rock classification[J].Journal of Xi’an University of Science and Technology,2005,25(1):12-16.
[14] 毛红阁,刘长旺,刘香伟,等.两层模糊神经网络交通信号控制模型[J].西安科技大学学报,2012,32(5):662-666.
MAO Hong-ge,LIU Chang-wang,LIU Xiang-wei,et al.A signal control model based on two-layer signal fuzzy neural network[J].Journal of Xi’an University of Science and Technology,2012,32(5):662-666.
[15] 刘洁,高佳,王绿.基于AHP的高校学报编辑评优[J].西安科技大学学报,2013,33(4):494-498.
LIU Jie,GAO Jia,WANG Lu.Editor assessment of university journal based on AHP[J].Journal of Xi’an University of Science and Technology,2013,33(4):494-498.
[16] 章正高.采用层次分析法对地质灾害进行危险性评价[J].西安科技大学学报,2014,34(1):87-91.
ZHANG Zheng-gao.Risk assessment of geologic hazards by analytic hierarchy process[J].Journal of Xi’an University of Science and Technology,2014,34(1):87-91.

