二元函数极限多种求解方法探析

刘丽娜（山西交通职业技术学院,太原030031）



二元函数极限多种求解方法探析

刘丽娜
（山西交通职业技术学院,太原030031）

摘要：函数极限是高等数学中非常重要的内容,尤其是二元函数极限,它是一个较为复杂的极限,其重点是研究极限的具体求解方法。文章对此进行讨论，总结了几种求解方法。

关键词：二元函数；极限；概念分析；求解方法；夹逼性准则

在多元函数微分学中，二元函数极限的求法既是重点内容又是难点内容之一。文章总结了二元函数极限的多种求解方法，并通过例题逐一说明。

一、二元函数极限概念分析

二、二元函数极限的求法

1.利用极坐标变换求二元函数的极限

解：令，则

例2求极限

2.利用连续性求极限

例3求

解：原式=0=0 1

例4

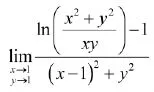
解：原式=

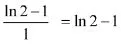
3.利用二元函数极限定义

在（0，0）的极限

解：当x，y沿y=x趋于零时

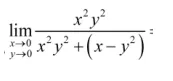
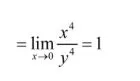
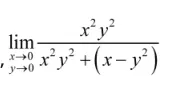
4.利用无穷小量与有界变量的乘积仍为无穷小量的结论

例7求

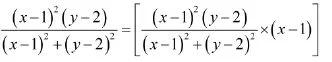
利用重要极限求极限时,关键在于设法凑成已知极限的形式。

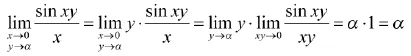
6.利用极限的夹逼性准则

类似于一元函数极限的夹逼性准则，可证明二元函数极限的夹逼性准则

7.利用分子或分母有理化

例10求

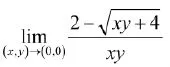
解：原式=

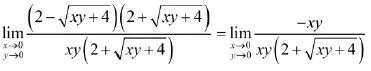
总之，只有掌握好基本的求解方法,运用好基本的运算技能,才能举一反三，对症下药,解决具体问题,从而真正的掌握好所学知识。当然二元函数极限的求解方法还有很多，但万变不离其宗,笔者就不一一列举了。

参考文献：

[1]同济大学应用数学系.高等数学（第五版）[M].北京：高等教育出版社，2007.

[2]几米多维奇,数学分析习题集题解[M].济南：山东科技出版社，1999.

[3]刘玉琏,傅沛仁.数学分析讲义[M].北京：高等教育出版社，1997：144-156.

[4]同济大学应用数学系.高等数学[M].北京：高等教育出版社，2006：69-7.

编辑郑晶

作者简介：刘丽娜（1982-），女，山西大同人，研究生，山西交通职业技术学院助教，研究方向为数学与应用数学。

收稿日期：2014-12-30

文章编号：2095-8528（2015）04-081-02

文献标识码：A

中图分类号：O13