基于混沌粒子群K-means 算法的人员分类训练

王伟 刘付显

(空军工程大学 防空反导学院，陕西 西安710051)

1 引言

在组织军事训练过程中，根据受训人员各项考核指标的成绩对人员进行合理分类，为不同类别人员制订针对性的训练计划，避免“一锅煮”，是提高训练效果的有效方法。体能训练作为军事训练的重要内容，其关于分类训练方法的研究也一直备受关注。

在理论研究方面，文献［1］对军事体能训练问题进行分析并提出对策思考;文献［2］分析了规范体能训练管理机制的方法;文献［3］对中美两军体能训练评价分类方法进行了对比分析;文献［4］提出了基于灰色马尔科夫理论的体能训练效果预测与评价模型。分析可知，目前大部分文献对分类训练的研究处于定性阶段，定量化分析的研究很少，因此对实际训练的指导性不强。在实际训练中，对人员的分类主要根据单项运动成绩进行划分，区分为两级(合格、不合格)或四级(优秀、良好、合格、差)，存在分类标准固化，不能根据受训对象水平灵活调整的问题，因此分类的针对性不强，量化和精细化不足，不能充分挖掘人员数据信息。

在信息化条件下，充分利用军事资源数据，强化军事训练精细化管理，突出量化分析是军事训练的重要发展方向。因此，研究利用人员测试数据信息进行合理分类训练是提高军事训练科学化水平的重要途径。由MacQueen 提出的K -means 算法是目前应用最广泛的一种聚类方法，但传统的Kmeans 算法存在对初始聚类中心敏感、易陷入局部最优、聚类数k需要事先给定等不足［5］。为克服K- means 算法的不足，研究人员提出多种粒子群优化聚类算法:文献［6］首次提出了结合K 均值算法和粒子群优化算法解决聚类问题;文献［7］提出了粒子群聚类算法的编码与适应度选择方法;文献［8］提出了两阶段混合粒子群优化聚类方法，给出了一种简化的粒子编码方法;文献［9］提出一种基于同步学习架构的粒子群聚类算法。目前，多种粒子群优化聚类算法已被应用于财务预警、IDS 告警聚类和客户分类等领域，但在人员训练分类中的研究还很少。

本文将K - means 算法、粒子群、混沌思想相结合，对人员体能训练的分类问题进行研究。首先，对所提算法进行描述;然后，应用来自权威的UCI数据对算法分类准确性和稳定性进行检验;最后，运用所提算法对一组体能测试数据进行聚类分析，为制订科学的训练计划提供依据。

2 混沌粒子群K - means 算法

2.1 K - means 算法

数据样本集X中有n个待分类对象，每个对象有d个特征指标，即X ={xi| xi∈Rd，i =1，2，…，n}，将其划分为k个类sj(j =1，2，…，k)，各类中心为为类sj中对象的个数，并使得各样本点与对应聚类中心的距离之和J最小:

式(1)中，d(xi，cj)为样本点到对应聚类中心的欧式距离:

2.2 粒子群优化算法

粒子群优化［10］(PSO)算法是一种模仿鸟群觅食行为的群智能算法，优化问题的每个解都是搜索空间的一只“鸟”，称为“粒子”，每个粒子都有对应的位置、速度和由目标函数决定的适应度。算法首先初始化粒子群，然后粒子通过不断调整自己的位置来搜索最优解。在每次迭代中，粒子通过跟踪两个“极值”来更新自己。一个是粒子本身所找到的最优解称为个体极值(pbest)Pi，另一个是整个种群目前找到的最优解称为全局极值(gbest)Pg，粒子根据下面两个公式更新速度和位置:

式(3)、式(4)中，vid为第i个粒子在第d维上的速度，ω为惯性权重，c1和c2为学习因子，r1和r2为0 到1 之间均匀分布的随机数。

在PSO 中，惯性权重的选择对算法收敛性有直接影响，较大的ω有利于全局搜索，较小的ω有利于进行精确的局部搜索［11］。本文采用自适应的惯性权重，每个粒子的惯性权重根据其适应度值的变化进行调整。当粒子的目标值与群体最优值差别较大时，采用较大的ω，使该粒子能够更快地趋向较好的搜索空间，以加快搜索速度;当粒子的目标值与群体最优值差别较小时，采用较小的ω，使粒子得到保护，以提高搜索精度。自适应惯性权重设置如下:

式(5)中，ωmax和ωmin分别为ω的最大值和最小值为第i个粒子在第t代的目标值和分别为种群最优目标值和最差目标值。

2.3 混沌PSO 算法

由于标准PSO 算法存在早熟收敛的缺陷，而混沌运动具有随机性、遍历性、对初始条件敏感性等特点，因此，将混沌思想引入PSO 算法，帮助惰性粒子逃离局部极小点，并快速搜寻到最优解。选用经典Logistic 映射［12］:)

当μ =4 时，式(6)产生的序列处于完全混沌状态，初始变量x0的微小变化将导致后续轨道的巨大不同。由任意初值x0，可迭代出一个确定的序列x1，x2，x3，…。

对种群全局最优粒子执行混沌搜索以产生混沌序列，用新产生的混沌序列粒子替代原种群粒子，避免PSO 陷入局部最优。

2.4 聚类数k 确定

聚类数k关系聚类结果的有效性，好的聚类应使类内的对象具有最大的相似性而类间的对象具有最大的相异性。应用距离代价函数作为空间聚类有效性检验函数［13］:

式(7)中，c0为全部样本的均值。当距离代价函数达到最小值时，聚类数k为最优。

2.5 混沌粒子群K - means 算法流程

在粒子群聚类算法中，每个粒子的位置由k个中心组成，样本向量维数为d，因此粒子的位置是k× d维向量，粒子的速度也是k × d维向量，粒子位置编码构造如下［5，7］:

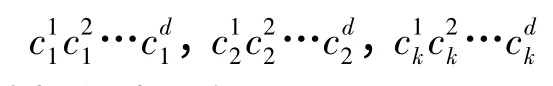
算法的操作步骤如下:

第1 步:初始聚类数k =1(经验规则

第2 步:种群初始化。①将数据样本集随机划分为k类，并计算各类的聚类中心，作为初始粒子的位置编码，并随机初始化粒子的速度，反复进行N次，共生成N个初始粒子;②按式(1)计算各粒子的适应度;③令各粒子的本身位置为其初始最佳位置pbest;④令种群中具有最优适应度的粒子的位置为初始种群最佳位置gbest。

第3 步:进行基于PSO 算法的搜索。①根据群体中各粒子的适应度，更新各粒子自身的最佳位置信息pbest;②根据群体中各粒子的最佳位置，更新群体最佳位置信息gbest;③对于每个粒子，按式(3)和式(4)更新粒子的速度和位置;④对于每个粒子，计算新位置的目标值J。

第4 步:粒子淘汰。将所有N个粒子按适应度大小进行排序，淘汰后50%的粒子。

第5 步:进行混沌搜索。对于群体中的最佳微粒gbest，按式(6)执行混沌搜索，产生0.5N个新粒子用于补充已淘汰的粒子。

第6 步:应用K 均值聚类算法对粒子位置进行优化。①根据每个粒子的位置编码，按照最近邻原则，来确定对应于该粒子的聚类划分;②利用K 均值较强的局部搜索能力，按照聚类划分计算新的聚类中心，用于更新粒子位置。

第7 步:若达到结束条件(足够好的位置或最大迭代次数)，则对应此聚类数k的寻优过程结束，并计算距离代价函数F(s，k)，转第8 步;否则，转第3 步。

3 算法验证

为了测试本文提出的新算法对数据的分类性能，采用来自权威的UCI 数据库的2 组数据集Iris和Glass 进行试验［14］，它们经常被用来检验聚类算法的有效性。Iris 数据集样本的4 个特征分别表示Iris 数据的花瓣长度、花瓣宽度、萼片长度和萼片宽度，共3 类;Glass 数据集样本含有9 个特征，分别代表玻璃碎片的折射率及如Na、Mg、Al 等8 种物质的氧化物的百分含量，共6 类，每类包含样本的数目相差较大。数据集详细信息见表1。

表1 数据集信息

3.1 算法聚类准确性评价

采用常用的纯度标准作为聚类结果的准确性评价［8］。设类簇Ci的大小为ni，则该类簇的纯度定义为:

式(8)中，nij为类簇Ci与第j类交集的大小。整个聚类结果的纯度Purity定义为:

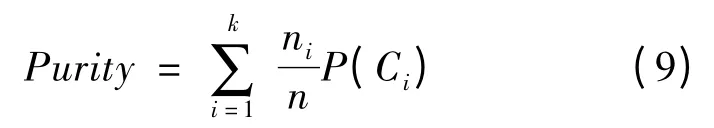
式(9)中，nij为类簇的数量。纯度反映了聚类算法分类的准确性，纯度越高，聚类算法越准确。

粒子群优化参数设置如下:粒子群种群规模N=30，学习因子c1= c2=2.05，惯性权重ωmax =0.9，ωmin =0.4，最大迭代次数t =50。运行本文算法30 次，计算聚类结果纯度的平均值，与其他聚类算法结果比较，见表2。

表2 4 种算法聚类纯度比较

从表2 可看出，本文算法在两个数据集上都取得了最高的聚类纯度，其中，Iris 数据集的样本数和类别数较少，粒子位置编码的维数较低(12 维)，聚类效果较好;Glass 数据集样本数和类别数较多，粒子维数较高(54 维)，算法寻优难度增大，影响了聚类纯度。

4 种算法在Iris 和Glass 两个数据集上进行聚类的收敛过程分别如图1 和图2 所示。

从图1 和图2 可看出:PSO 算法较快地陷入局部最优;K -means 算法和PSO -Kmeans 算法的全局搜索能力有所增强，但仍易陷入局部最优;本文算法继承了K - means 算法收敛快的优点，同时混沌操作的引入增强了算法全局寻优能力，在迭代200—300 步时，粒子仍然能跳出局部最优点趋于全局最优，从而提高了算法的聚类性能。

图1 Iris 数据集的分类目标函数收敛曲线

图2 Glass 数据集的分类目标函数收敛曲线

3.2 算法稳定性评价

采用30 次试验中目标函数J的方差作为聚类算法的稳定性评价。4 种算法在Iris 和Glass 两个数据集上对样本数据进行聚类时的稳定性结果见表3和表4。

表3 Iris 数据集的聚类结果稳定性比较

表4 Glass 数据集的聚类结果稳定性比较

从表3 和表4 可看出，本文算法寻优的最大值、最小值、均值和方差均优于其他算法，说明本文算法的寻优能力和稳定性较好，能有效避免早熟收敛和对初始值敏感的问题。

综合以上分析可知，本文算法具有较高的聚类准确性和稳定性，能够应用于实际分类问题。

4 应用混沌粒子群K - means 算法的人员分类训练

4.1 数据描述

现代战场环境对参战人员的体能提出了更新、更高的要求，《中国人民解放军军人体能标准》中要求的体能训练内容包含速度、耐力、力量、柔韧、灵敏等方面，体能考核的主要项目包括:5 公里、单杠、100 米跑、立定跳远、50 米折返跑，通过以上5 项指标可反映受训人员体能的综合情况。仿真计算所用样本数据为100 名受训人员的体能测试数据，每个数据包括上述5 项考核指标，各项指标测试成绩见表5。

表5 人员各项指标测试成绩(部分)

4.2 数据预处理

由于不同测试指标采用不同的度量标准，需对原始数据进行预处理。采用极差预处理方式，将数据映射到［0，1］区间。为保证所有指标标准化后方向上的一致性，对于成本型指标，如5 公里、100 米跑、50 米折返跑等，采用如下变换:

由于不同测试指标重要程度不同，对聚类结果的影响也不相同。通过咨询专家意见并采用AHP法计算5 项指标权重为ω =(0.298，0.276，0.163，0.118，0.145)。修正式(2)为加权欧式距离［8］:

式(12)中，ωm为第m个指标的权重。

4.3 仿真计算

应用本文所提算法对处理后的100 名受训人员体能测试数据进行聚类，算法参数设置同上文。通过计算距离代价函数值来确定最佳聚类数k，距离代价函数随聚类数k的变化曲线如图3 所示。

图3 距离代价函数随k 变化曲线

由图3 可知，算法在聚类数为4 时，距离代价函数最小，F(s，k)*=28.666，从而确定最佳聚类数为4。此时，目标函数收敛曲线如图4 所示。

图4 目标函数收敛曲线

种群最优粒子的位置编码即为4 个聚类中心点cj，根据式(10)、(11)将cj还原为原始类型数据，聚类结果见表6。

由表6 可知，100 名受训人员被分成A、B、C、D四类，并得到各类别的人数，并且各聚类中心点可反映对应类别人员体能的总体情况。组训者可根据各类别人员的成绩和人数，制定针对性的训练计划，以满足不同类别人员的训练需求，解决了组训中训练量过大“吃不好”和训练量过小“吃不饱”之间的矛盾，并且可以针对短板强化训练，提高训练效率。

表6 聚类结果

4.4 算法对比实验

为了对比分析本文算法与传统四级制分类法，并且鉴于四级分类法通常只考虑单项运动成绩，因此仅以5 公里数据集为例进行仿真实验，四级分类法根据优、良、合格、差的分界标准进行分类划分。两种方法的分类结果见表7。

表7 分类结果对比

由表7 可知，本文算法比四级分类法具有更小的目标函数J，即各样本点与对应聚类中心的距离值更小，因此分类效果更好。

通过综合分析，应用本文算法对体能训练进行分类具有以下优点:

(1)通过本文算法将人员划分为多个类别，可避免训练“一锅煮”的问题。

(2)本文算法能够充分利用数据信息，进行多指标综合评价分类，并且各类别的分类标准是根据实际数据得出的，解决了传统方法分类标准固化的问题，避免分类标准的“一刀切”。

(3)本文算法分类效果好，类内的对象具有最大的相似性，类间的对象具有最大的相异性，解决了“分不清”的问题。

(4)应用本文算法可得到受训人员的理论最佳分类数，但同时可根据训练组织者的实际情况对分类数进行随机调整，当组训人员充足时可适当增加分类数，当组训人员缺乏时可适当减小分类数。

5 结束语

针对人员训练过程中的分类问题，本文提出一种混沌粒子群K 均值聚类算法，实验结果表明，与K-means 算法、粒子群聚类等算法相比，该算法具有更高的分类准确性和稳定性。采用本文算法对人员训练数据进行聚类分析，充分挖掘数据信息，客观合理地将受训人员进行分类，对不同类别人员制订不同的训练计划，与传统分类方法相比具有分类效果好、分类标准灵活等多个优点。提高训练的数据意识和量化观念对提高训练科学化水平至关重要，本文的量化分类方法能够为科学化组训提供一定的决策支持。该方法具有一定的通用性，可用于其他类似军事训练问题，例如装备操作训练、军事技能训练等。

［1］ 李忠，李铁钢，李益，等. 军事体训练问题分析及对策思考［J］.高等教育研究学报，2012，35(2):24 -26.

［2］ 陈应表.美俄军队体能训练及启示［J］. 军事体育学报，2013，32(3):23 -26.

［3］ 黄为根.中美军体能训练评价的对比研究［J］.军事体育进修学院学报，2012，31(2):75 -77.

［4］ 彭勇.基于灰色马尔科夫理论的体能训练效果预测与评价模型［J］.军事运筹与系统工程，2013，27(3):59 -61.

［5］ 陶新民，徐晶，杨立标，等. 一种改进的粒子群和K 均值混合聚类算法［J］.电子与信息学报，2010，32(1):92 -97.

［6］ VAN DER MENWE D W，ENGELBRECHT A P. Data clustering using particle swarm optimization［C］// Proceedings of Evolutionary Computation. Piscataway:IEEE Press，2003.

［7］ 刘靖明，韩丽川，侯立文.基于粒子群的K 均值聚类算法［J］.系统工程理论与实践，2005，22(6):54 -58.

［8］ 王纵虎，刘志镜，陈东辉.两阶段混合粒子群优化聚类［J］.西南交通大学学报，2012，47(6):1034 -1040.

［9］ LIU RUOCHEN，CHEN YANGYANG，JIAO LICHENG，et al.A particle swarm optimization based simultaneous learning framework for clustering and classification［J］. Pattern Recognition，2014，47(6):2143 -2152.

［10］ KENNEDY J，EBERHART R C. Particle swarm optimization［C］// Proceedings of the IEEE International Conference on Neural Networks. Piscataway:IEEE Press，1995.

［11］ 李军伟，程咏梅，陈克喆，等. 基于AIWCPSO 算法的三次样条气动参数插值方法［J］. 控制与决策，2014，29(1):129 -134.

［12］ LIU BO，WANG LING，JIN YIHUI，et al. Improved particle swarm optimization combined with chaos［J］. Chaos，Solitons and Fractals，2005，25(5):1261 -1271.

［13］ 杨善林，李永森，胡笑旋，等.K-means 算法中的k 值优化问题研究［J］.系统工程理论与实践，2006，23(2):97 -101.

［14］ UC Irvine. UCI Machine Learning Repository［EB/OL］. ［2015-01 -06］. http://archive.ics.uci.edu/ml/datasets/